基于EMD的IMF时域统计特征提取及其应用于震动事件源类型识别研究
2022-01-26薛思敏黄汉明施佳鹏袁雪梅黎炳君广西师范大学计算机科学与信息工程学院广西桂林54100
薛思敏, 黄汉明, 施佳鹏, 袁雪梅, 黎炳君(广西师范大学计算机科学与信息工程学院, 广西 桂林 54100)
0 引言
人工爆炸和天然地震振动产生的波形非常相似。各地震观测台站记录的事件波形数据含有人工爆炸、泥石流、山体隧道等其他事件的波形信息,这些混有非天然地震事件的波形记录会混淆地震目录,若对这些波形处理不当会对地震学的研究造成影响。如何快速、准确地从震源事件震动波形中识别出天然地震事件与人工爆炸事件是地震学研究及相关应用领域亟待解决的问题。
天然地震与人工爆炸信号都属于非线性、非平稳信号。自二十世纪五十年代开始,国内外学者进行了许多提取蕴藏在噪声时间序列的该信号的特征来进行天然地震和非天然地震分类识别方法研究,并提出了多种识别依据,如希尔伯特-黄变换谱在地震信号分析中的应用[1],将HHT与Fourier分析进行比较,显示了HHT方法的优越性;基于经验模态分解的地震P波初至自动识别研究[2],将前三个IMF分量和趋势项合成新的地震信号,采用递归STA/LTA方法识别地震P波初至点,其精确度较高;天然地震与人工爆炸波形信号HHT特征提取和SVM识别研究[3],提取分解后前3个IMF分量的最大幅值对应周期和倒谱平均值,采用SVM分类识别,识别率较好;基于聚类经验模态分解(EEMD)的汶川MS8.0强震动记录时频特性分析[4],将数据进行EEMD和Hilbert变换及谱分析,发现采用EEMD可以抑制EMD中存在的模态混叠问题;地震波形的HHT特征提取和GMM识别研究[5],使用GMM对提取前三个IMF分量的MFCC特征分别进行分类识别,得出第一个分量提取的MFCC特征识别效果最好,可以作为分类识别有效判据。
传统的信号处理方法如小波变换、傅里叶变换在使用时,都要预先选取合适的基函数。经验模态分解方法依据数据自身的时间尺度特征来进行信号分解,无须预先设定任何基函数。正是由于这个特点,EMD方法在理论上可以应用于任何类型的信号的分解,因而在处理非平稳及非线性数据上,具有非常明显的优势。
1 经验模态分解和内模函数
希尔伯特-黄变换(Hilbert-Huang Transform,简称HHT)是美籍华人N.E Huang等[6-10]提出的一种信号分析方法,其核心思想是将时间序列信号通过经验模态分解(Empirical Mode Decomposition,简称EMD),得到有限个内模函数(intrinsic mode function,简称IMF),再对内模函数进行希尔伯特变换,从而得到该信号的希尔伯特谱、时频能量谱等,以便对信号进行分析。该方法对非线性、非平稳信号有较好的分析和处理效果。
经验模态分解是假设任何复杂的信号都是由简单固有模态函数组成,是以局部时间尺度为基础的。经验模态分解是将数据集分解为个数有限的内模函数IMF的线性叠加。
每一个IMF不论是线性或者是非线性、平稳或是非平稳的,都具备以下两个条件:在整个信号波形中,极点个数和过零率的个数必须相等,或最多相差不能超过一个;在任意时刻,由局部极大值点形成的上包络线和由局部极小值点形成的下包络线的平均值为零,即上、下包络线相对于时间轴局部对称。我们可以在上述的基础上,采用模态分解方法通过下面的步骤对任何信号x(t)进行分解[11-16]:找到信号x(t)所有的极大值点并利用三次样条函数插值拟合成原数据序列的上包络线v1(t);找出信号x(t)所有的极小值点并利用三次样条函数插值拟合成原数据序列的下包络线v2(t),并求出其上包络线和下包络线的平均值m1(t)。其公式为:
(1)
将原数据序列减去包络平均值后即可得到一个去掉低频的新数据序列。其公式为:
h1(t)=x(t)-m1(t)
(2)
判断h1(t)是否为IMF函数。若不满足IMF条件,将h1(t)看作新的信号序列,重复上述处理过程,直到h1(t)满足条件时,记c1(t)为IMF1。其公式为:
c1(t)=h1(t)
(3)
令:
r(t)=x(t)-c1(t)
(4)
看作新的信号序列,重复h1(t)的判断步骤,即可得到不同结果的IMF分量,直到满足给定的终止条件时筛选结束。原始的数据序列即可由这些IMF分量以及一个剩余项r(t)表示,即:
(5)
式(5)说明,可以将信号x(t)分解成频率从大到小也即变化由快到慢排列的n项IMF分量与一个剩余项r(t)之和。由于每一个IMF分量代表一个特征尺度的数据序列,因此筛选的过程实际上是将原来数据序列分解为各种不同特征波动序列的叠加。
经验模态分解的过程其实就是一个筛选的过程,在筛选的过程中不仅消除了模态波形的叠加,而且使波形轮廓更加对称。在天然地震和人工爆炸信号分析中,利用经验模式分解不需要固定的基函数,可将原始信号分解为若干个频率自高到低排列的内模函数,其分解过程具有高效性、自适应性。
2 KL距离
KL距离能够有效衡量两个概率分布之间的距离。若这两个概率分别为离散随机变量P(xi)和Q(xi),xi是随机变量,则KL距离可定义为:
(6)
式中:KL(P(xi)‖Q(xi))表示两个概率密度函数P(xi)与Q(xi)似然比的对数期望,也称相对熵(relative entropy)。当且仅当两概率分布完全相同时,相对熵KL(P(xi)‖Q(xi))最小且为零。由于相对熵不具有对称性,概率分布P(xi)与Q(xi)的相对熵距离通常并不等于从Q(xi)到P(xi)的距离。
定义一种对称的KL距离来衡量这两个概率分布的相似度[17-19]:
d(P(xi),Q(xi))=KL(P(xi)‖Q(xi))+
KL(Q(xi)‖P(xi))
(7)
式中:P(xi)表示提取天然地震或人工爆炸数据特征值按概率分布形式来表达的矩阵;Q(xi)表示提取天然地震或人工爆炸数据特征均值按概率分布形式来表达的矩阵;d(P(xi),Q(xi))表示P(xi)与Q(xi)概率分布之间的相似度。
本文利用KL距离对微小异常的敏感性,采用对称的KL相似度,考虑天然地震数据特征值按概率分布形式表达的矩阵与天然地震数据特征均值按概率分布形式表达的矩阵之间的距离(d1),以及天然地震数据特征值按概率分布形式表达的矩阵与人工爆炸数据特征均值按概率分布形式表达的矩阵之间的距离(d2),将两个距离进行比较,若d1 实验中所用的天然地震记录样本和人工爆炸记录样本均选取于三河市2010—2016年发生的地震记录。其中有16个天然地震事件,共131条数据记录;有17个人工爆炸事件,共186条记录。在实际的天然记录样本和人工爆炸记录样本中有一些记录采样点的数据幅值为0的,本文作者认为是无效数据。最终本文共得到307条天然地震和人工爆炸波形记录的数据作为实验原始数据。 本文对真实的天然地震和人工爆炸事件的三分量波形提取特征。我们对波形数据进行归一化预处理,采用EMD方法将原波形信号分解为7个内模函数和1个残差函数,对原波形、每个内模函数和残差函数分别提取26个时域统计特征,组成9个特征组(Q0、Q1、…、Q8);再计算7个内模函数的幅度能量比得到7个能量比特征,选择前4个内模函数的26个时域统计特征中的8个特征共32个特征组成一个有39个特征的特征组。如图1为序号37的天然地震事件HE.XIL台站记录的垂直波形数据分解得到的内模函数(IMF)和残差函数,图2为序号147的人工爆炸事件BU.LBG台站记录的垂直波形数据分解得到的内模函数(IMF)和残差函数。 图1 天然地震的EMD分解Fig.1 EMD of natural earthquake 本文前述的Q0、Q1、…、Q8特征组中的26个时域特征都是某种统计特征,它们分别是:描述样本集中程度的量值:算数均值、中位数、模态数、截尾均值、调和均值;描述样本散布程度的量值:四分位差、标准方差、平均绝对值、各阶中心距(3~9阶中心距,共7个中心距);描述样本分布偏离正态性的量值:偏斜度、峰度、分位数(共9个分位数)。其公式如下: 均值 (8) 调和均值 (9) 四分位差 (10) 平均绝对值 (11) 图2 人工爆炸的EMD分解Fig.2 EMD of artificial explosion 标准方 (12) 中心距值 mi=E(x-E(x))i,i=3,4,…,9 (13) 偏斜度: (14) 峰度: (15) 式中:x表示信号数据;i表示第i个数值;n表示一段地震波段的采样点数;E(x)表示期望值。 为了避免事件强度差异的影响(事件强度差异会造成波形幅值范围显著不同,从而使事件类型识别结果很可能只依赖于事件的强度),计算这些时域统计特征前,原观测波形需先进行归一化,即每一份波形取值范围规范化为界于[-1,1]。 本文阐述的Q9特征组的39个特征,分别是:由7个内模函数的幅度能量比得到7个能量比特征,如式(16);前4个内模函数的26个时域统计特征中的8个特征,分别为算数均值、中位数、四分位差、标准方差、偏斜度、峰度、3阶中心距及4阶中心距。 (16) 本文采用对称KL距离分类识别方法,首先由于提取的各个特征矩阵可能存在权重不等的问题,也为了剔除不同记录波形的样本点幅值有显著差异的影响,应将特征数据集中的所有特征进行预处理,所以以列为单位对天然地震和人工爆炸分别归一化处理,采用的公式为: (17) 式中:X表示m行n列的特征值矩阵;Xmax、Xmin也是m行n列的矩阵,这2个矩阵任一个的每一行与同矩阵的其他行都是完全相同的,Xmin/Xmax矩阵的每一行的各元素分别是X矩阵相应列的最小值/最大值。 本文对这10组特征样本集以事件为识别单元进行了单组、多组的特征组合事件类型识别实验,采用随机选择部分(30%,50%,70%,90%)事件即作为训练集,同时也作为测试集,对每次选定的百分比都反复进行了1 000次的实验(每次实验,16个地震和17个爆炸事件必须各被选中一个,还有其他215=32 768和216=65 536个可能被选中的事件组合)。由于每次都是随机划分得到训练样本和测试集样本,为了更好地识别结果以及检验特征的有效性,本文分别求正确识别率的1 000次随机抽样的平均值、方差、最大值和最小值四个统计参数,其中各统计量的计算公式为: 平均值 (18) 方差 σr=std(r1,…r1 000) (19) 最大值 r(max)=max(r1,…r1 000) (20) 最小值 r(min)=min(r1,…r1 000) (21) 其中:r1…r1 000表示每次的特征识别结果。其识别效果统计量如表1所列,与其他实验对比结果如表2所列。 其中,Q2(90%)和Q2、Q9(90%)表示随机选取事件的90%进行实验。Q2(90%)特征组的识别率高于2016年王永康[20]和2012年毕明霞[3],稳定性也高于王永康的实验结果;Q2、Q9(90%)特征组的识别率高于2012年毕明霞的实验结果,稳定性高于王永康和毕明霞的实验结果。 表1 识别效果的统计量 表2 实验对比结果 本文实验所用的数据集包含有16个地震事件的121条波形信号,17个爆炸事件的186 条波形信号。采用随机选择部分(30%,50%,70%,90%)事件即作为训练集同时也作为测试集,反复进行了1 000次的实验,结果表明第2个内模函数提取的时域统计特征在选择90%事件作为训练集和测试集的识别效果最好。从表1容易看出,无论哪个特征组,训练集合所选的事件数目占全部事件的比例越高识别效果越好;Q2、Q9特征组的组合明显比其中任意一个特征组的识别效果更好。本文的实验所用数据集的事件数目不多,只在原信号和IMF的时间域上进行了特征提取,但采用了随机有回放的采样实验,结果比较理想,且具有一定的推广性,值得在取得更多事件的数据集后进一步深入探讨。另外,IMF也可认为是某种频率分解成分,所以本文的时域特征里也已蕴涵有频率信息,且分解得到的IMF具有自适应滤波性,这很可能就是 2ndIMF具有明显较好识别性能的原因。把IMF作为普通信号,再从其提取频域或时频特征,这也应该值得探讨。 致谢:中国地震局地球物理研究所“国家数字测震台网数据备份中心”为本研究提供地震波形数据[21]。3 实验与结论
3.1 数据集的选取
3.2 特征提取



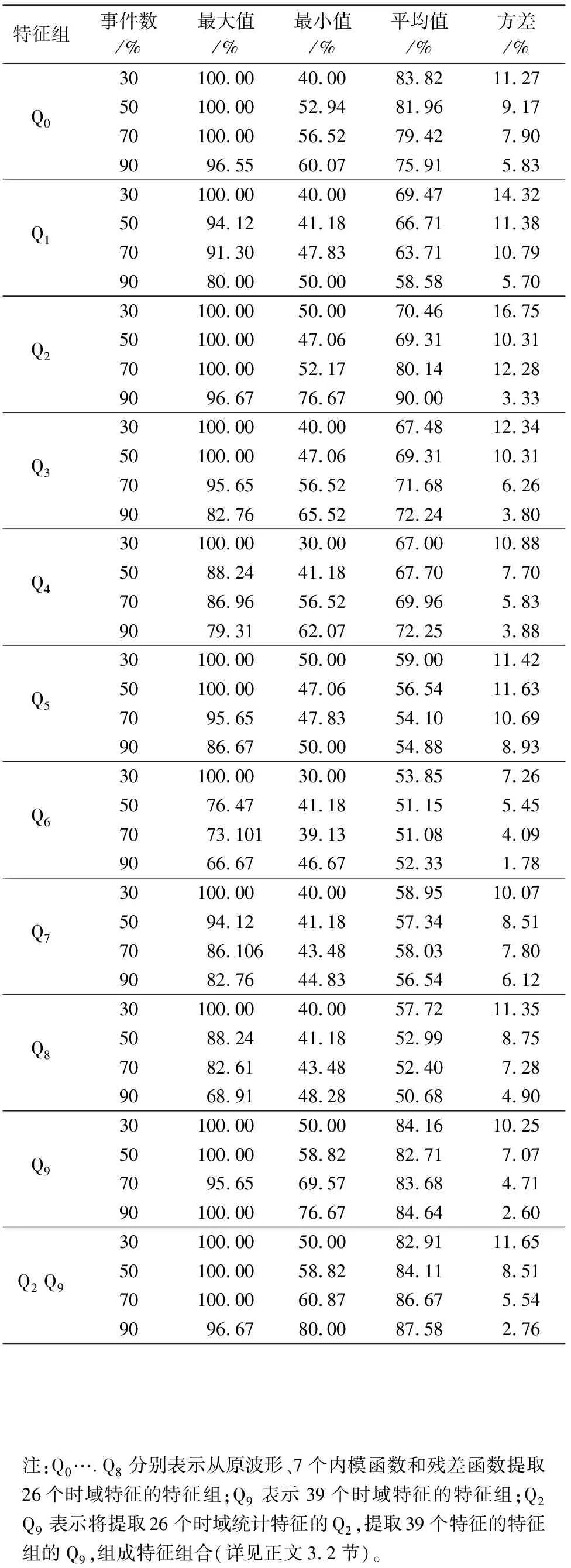
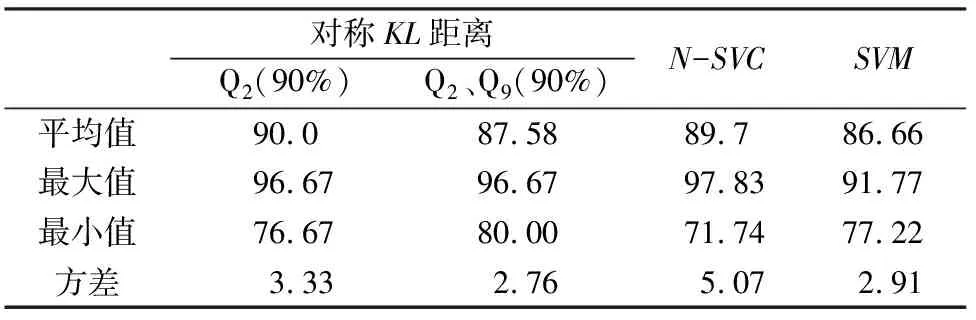
3.3 用对称KL距离对天然地震和人工爆炸信号进行识别
4 结论与讨论
