脉冲射流抑制叶栅二次流损失的数值研究

赵 树， 陈 榴， 戴 韧

(上海理工大学 能源与动力工程学院， 上海 200093)

在低展弦比透平叶栅中，端壁二次流带来的流动损失约占总损失的1/3以上[1]，其中前缘马蹄涡与通道涡[2]为二次流损失的主要组成部分。针对端壁二次流的多种被动流动控制方法[3-4]已得到大量应用。由于被动流动控制方法依靠改变透平叶栅的物理结构来改变内部流场的流动特性，其单一的运行工况与复杂的造型方法使得该控制方法存在一定局限性。这促进了流动控制方法的创新，使其向着射流这一主动流动控制方式的方向发展。

McAuliffe等[5]在低压透平的吸力面侧开设了一个吹槽，证明在低雷诺数和低湍流度下槽吹有助于抑制吸力面的流动分离，高湍流度下则无明显效果。虽然槽吹是一种非常有效的主动流动控制方式，但也是消耗射流质量流量最多的方式。Hansen等[6]在平板层流边界层注入稳态射流，发现有角度的射流更能带动低动量流体转变为高动量流体，也更有利于减少边界层的流动分离。Sondergaard等[7]将射流应用于低压透平的吸力面侧，在低雷诺数条件下射流可显著抑制吸力面边界层分离；在高雷诺数条件下没有产生显著的不利影响。相比于槽吹，稳态射流可以减少所需射流的质量流量[8]。随着稳态射流在透平叶栅的应用，一部分研究[9-11]将射流孔开设在吸力面侧，主要用于抑制吸力面侧的流动分离进而减少透平叶栅的总压损失；另一部分研究[12-14]则将射流孔布置在端壁上，主要用于端壁低动量流体的去除或者激励其为高动量流体，进而改变通道涡的发展路径，减少角区分离。

为了减少主动流动控制方法中对射流质量流量的需求，雷玉昌等[15]借助脉冲射流和定常射流的叠加效应有效缓解了翼型升力的脉动现象，同升力系数下脉冲射流可大量减少所需射流的质量流量。Bons等[16]通过使用高频电磁阀产生的脉冲射流，发现脉冲射流在流动控制方面的效果与稳态射流相当，但射流质量流量可以小一个数量级。Gross等[17]通过数值研究狭缝中的脉冲射流，发现脉冲射流的参数空间很大，需要搜寻不同射流函数的吹风比、占空比才能找到能量输入最小的流动控制参数。Benton等[18]通过在低压涡轮叶栅中设置4个非定常射流孔来减少所需质量流量，通过研究脉冲频率和占空比对端壁二次流的影响，发现脉冲射流可以有效控制端壁二次流。

考虑到方波函数是最能直接减少射流质量流量的函数，而正弦函数是不规则函数的基础的分解形式。因此，笔者在定常射流的基础上，研究方波函数与正弦函数射流在流动控制方面的非定常效应问题。以期能够合理控制方波函数射流中的占空比，使其在保持流动控制效果的同时尽量减少所需的质量流量；同时能够找到正弦函数射流中振幅、频率、时均动量系数的合理搭配方式，同样达到射流减少质量流量的效果。

1 物理模型与数值计算方法

1.1 物理模型与边界条件

以Langston平面叶栅[19]为研究对象，建立图1(a)所示的计算模型，Cax为轴向弦长，d为弦长，S为叶栅栅距，αin、αout分别为叶栅进出口安装角，βin为进口气流角；给定1.65Cax的进口域和1.5Cax的出口域，尾缘下游0.2Cax处平面为物理量的监测面；图1(b)给出了射流孔的物理模型；图1(c)给出了射流孔位置，其位置在前缘马蹄涡的流动分离线上，其中Line 1、Line 2、Line 3为叶栅前缘的法线。具体参数见表1。

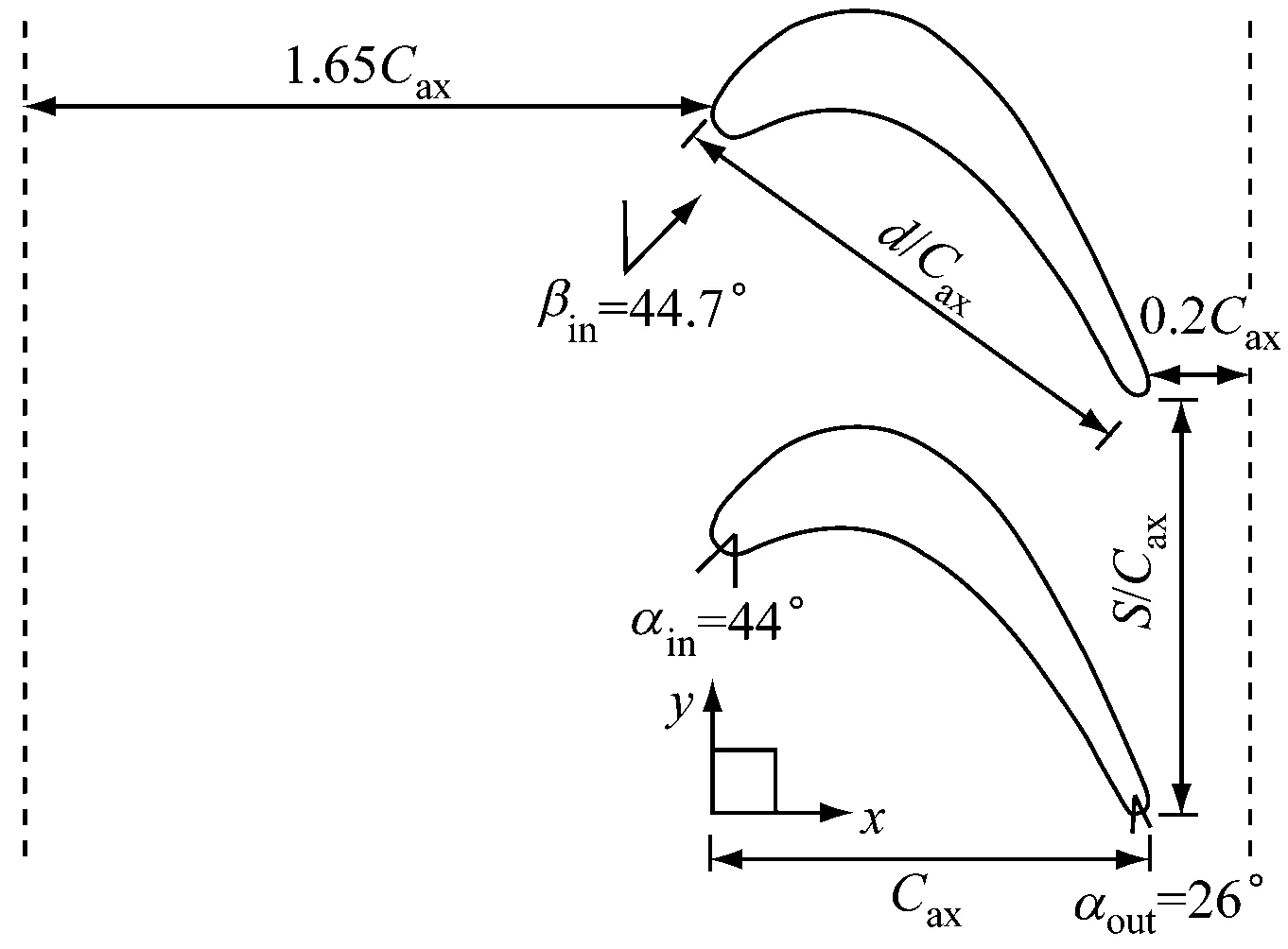
(a) Langston叶栅模型

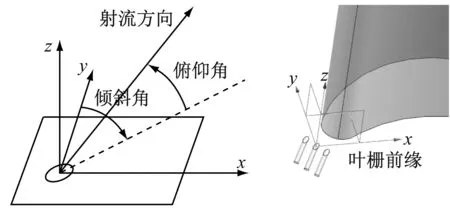
(b) 带射流孔模型

使用商业软件Ansys CFX 17.0，采用定常雷诺时均方程(RANS)对原始模型和带射流孔的模型进行数值计算。湍流模型采用SST模型。模型边界条件与文献[19]中的实验条件保持一致，实验工况参数见表2。

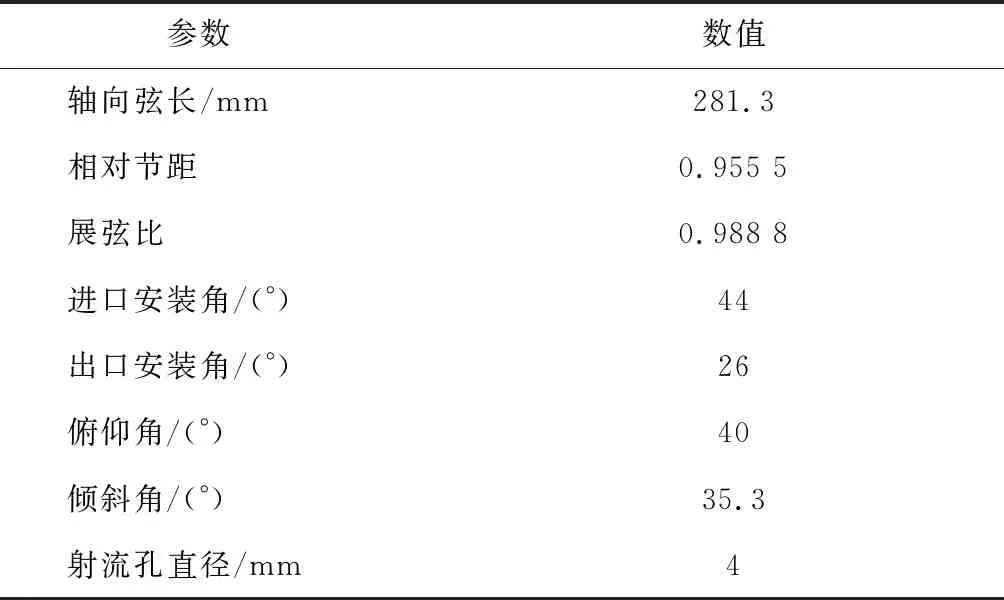
表1 透平叶栅叶型参数

表2 叶栅实验工况

进口速度表达式为：

(1)

式中：H为展向叶高；U0为进口主流速度；U为沿z轴分布的当地进口速度。

1.2 网格无关性验证和数值计算正确性验证

使用Pointwise软件对计算域进行网格划分。Langston叶栅四周采用O-H型网格，第一层网格厚度为0.01 mm，以1.2倍的增长率向四周扩展30层作为其边界层网格；射流孔周围采用非结构网格并通过拉伸使其在三维结构上成为三棱柱网格，满足端壁边界层网格的要求。网格划分如图2所示。

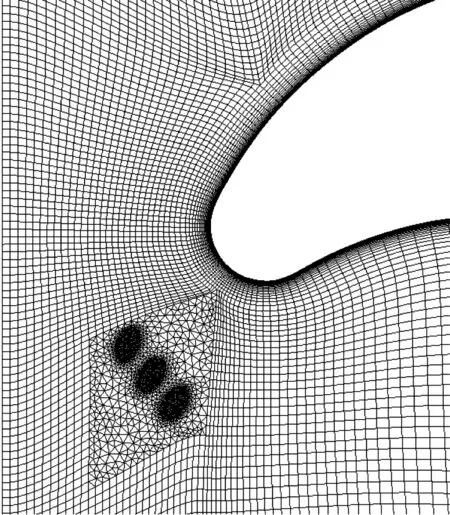
(b) 带射流孔网格

以Langston原始叶栅的出口截面质量流量加权的总压损失系数和二次流动能为参照量对比4个不同的网格数量模型，如表3所示，最终选取网格数量为3.28×106。在近端壁位置对网格加密，第1层网格厚度为0.01 mm，近端壁最大y+为2.289，满足计算要求。计算结果表明，沿3个坐标轴方向的速度残差均小于10-5，在800次迭代过程中出口质量流量加权平均总压变化率小于0.4%，说明计算结果收敛。

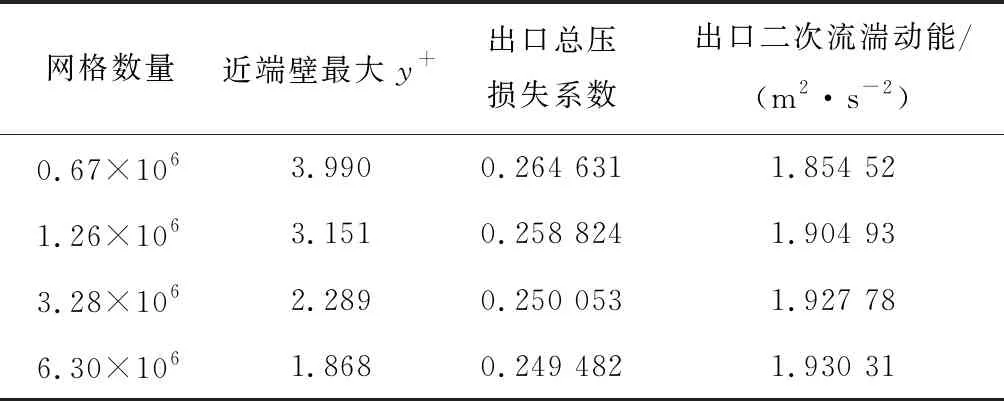
表3 网格无关性验证

图3给出了Langston叶栅沿叶型线展开的叶栅表面静压系数数值模拟结果和实验结果。对比图3(a)和图3(b)可知，数值模拟结果基本与实验结果相符。

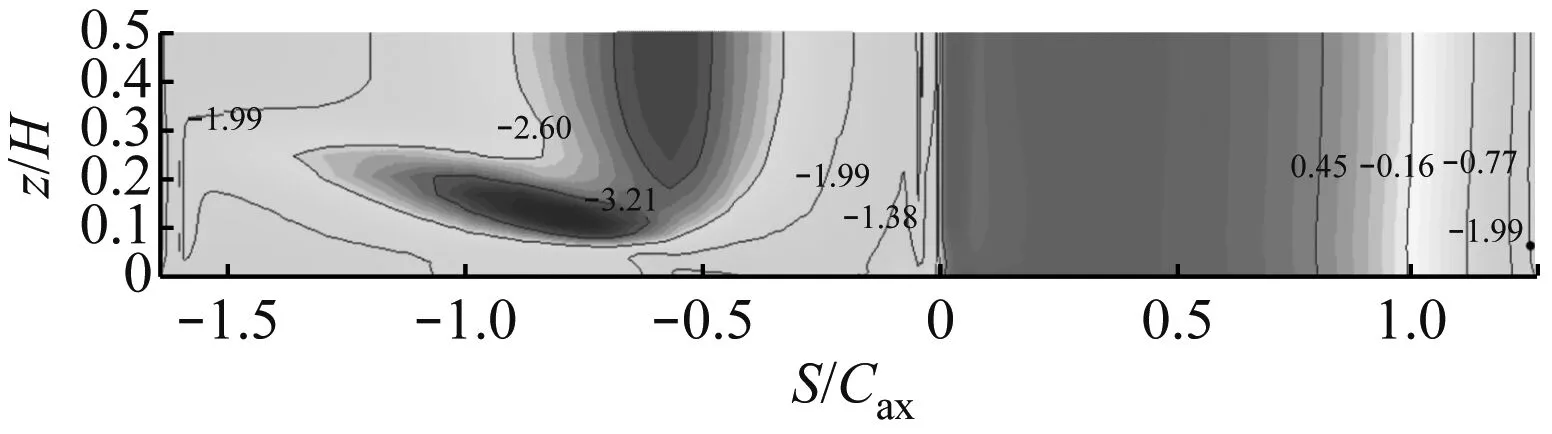
(a) Langston叶栅表面静压系数分布的数值模拟结果

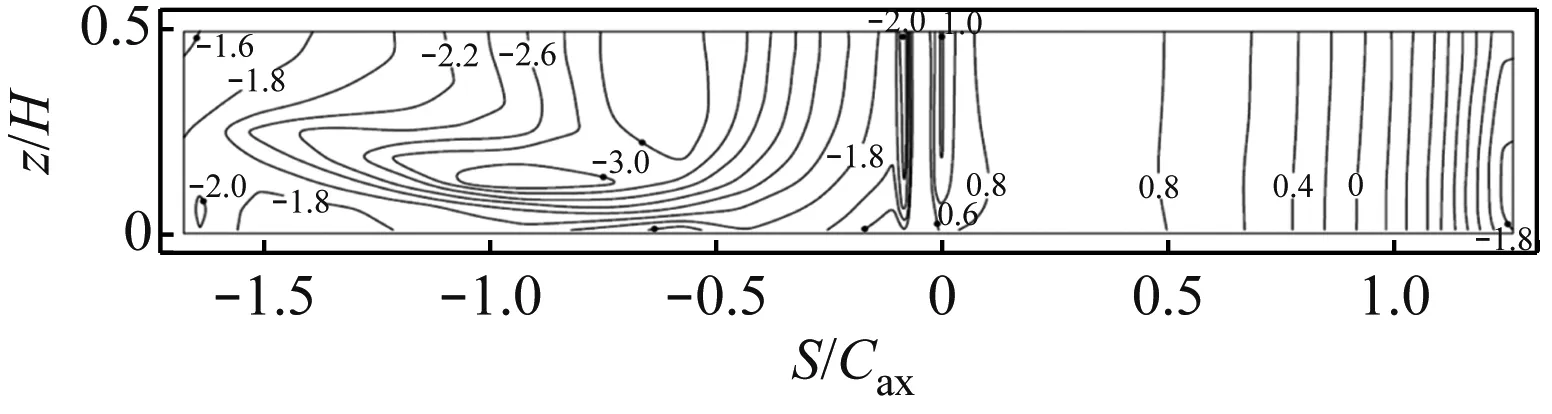
(b) Langston叶栅表面静压系数分布的实验结果

静压系数Cp表达式为：

(2)

式中：ps,local为当地静压；ps,in为进口气流静压；pt,in为进口气流总压。

1.3 非定常射流总压损失系数的计算方法

定义单个射流孔的时均动量系数为单个射流孔引入动量与主流动量的一半之比。其表达式为：

(3)

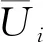
对于流动损失的判断依据，引入射流质量流量加权的总压损失系数，表达式如下：

(4)

(5)

(6)

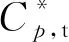
(7)

根据前期工作[20]可知，定常射流通过抑制前缘马蹄涡的流动分离，削弱了后续通道涡的强度，对端壁二次流的抑制起到了非常有效的作用。且当时均动量系数Cμ=0.10%时，射流孔对前缘马蹄涡的流动分离抑制效果最好。下文中以该定常射流为参考，对比脉冲射流对前缘马蹄涡的抑制效果。

2 方波函数射流

2.1 方波函数射流参数设计

在定常射流孔的基础上，通过改变射流随时间的变化来控制非定常函数的射流形式。射流函数的目的是在保证端壁二次流流动控制取得良好效果的前提下进一步减少能量的注入，因此方波射流函数是最为直接减少能量注入的方式，它通过改变一个周期内射流的有无来建立射流函数。

方波函数表达式如下：

(8)

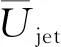
射流为方波函数时，

(9)

式中：U1为叶栅进口射流平均轴向速度分量；U2为叶栅出口射流平均轴向速度分量。

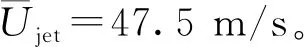
2.2 方波函数射流对端壁二次流的影响

图4为不同占空比下方波射流函数的总压损失系数分布。图中实线为Langston原始叶栅的总压损失系数，点划线是Cμ=0.10%时定常射流的总压损失系数，下同。从图4可以看出，射流占空比从0.2增加到0.4时，总压损失系数缓慢增大，且大于定常射流的总压损失系数，小于Langston原始叶栅的总压损失系数。当占空比增加到0.6时，总压损失系数开始降低且略小于定常射流的总压损失系数。当占空比大于0.6时，方波函数射流的总压损失系数略低于定常射流的总压损失系数，但整体变化幅度很小。因此，综合射流投入的能量与得到总压损失的收益来看，射流占空比为0.6时能够得到较大的综合收益。

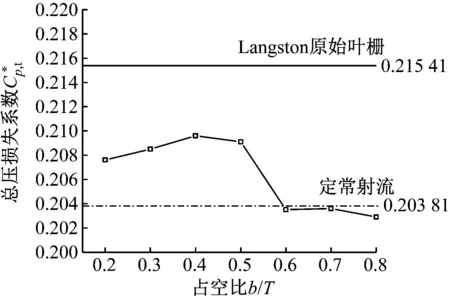
图4 不同占空比下方波函数总压损失系数分布

图5为占空比为0.6时，出口截面上2个周期的总压损失系数时域分布。由于在0.6T时刻射流突然消失，总压损失系数会发生跳闪。

0～0.6T的时间内，出口的总压损失整体上随射流的不断引入而降低，且低于Langston原始叶栅。但其总压损失在射流发生0.2T之后才开始低于定常射流，到0.6T之后由于射流不再存在，所以整体上出口的总压损失在不断升高，到0.9T时刻甚至超过了Langston原始叶栅的总压损失，但在一个周期内的时均总压损失基本上与定常射流持平。

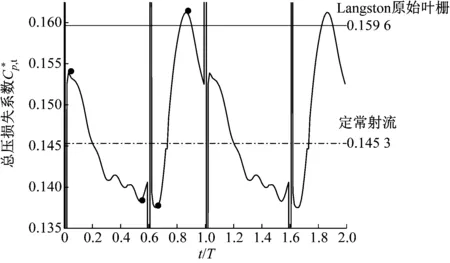
图5 占空比为0.6时的总压损失时域图

为分析方波函数射流在一周期内对Langston原始叶栅内流场的流动影响，选取图5中0.03T、0.54T、0.66T、0.86T4个时刻的流动状态进行分析。

图6为不同工况下前缘法平面湍动能及流线分布图，其中L/S为当地位置到叶栅前缘的相对距离。对比图6(a)和图6(b)可知，栅前端壁定常射流可抑制前缘马蹄涡的流动分离现象，并削弱前缘马蹄涡的湍动能，从而削弱了后续流道中的二次流损失。

图6(c)～图6(f)为一周期内4个不同时刻的流动状态。方波函数射流的非定常效应发生在0.66T时刻，此时射流从有到无，对应图6(d)过渡为图6(e)的时刻。可以看出，当射流消失后前缘马蹄涡的湍动能得到了削弱，在向图6(f)发展的过程中，不仅削弱了湍动能同时也抑制了前缘马蹄涡的流动分离。这是因为射流突然消失后，原本有射流的位置会产生一个低压区，四周的流体在压力的作用下向该处补充，很大程度上抑制了该位置的流动分离现象，进而削弱了其湍动能。

(a) Langston原始叶栅

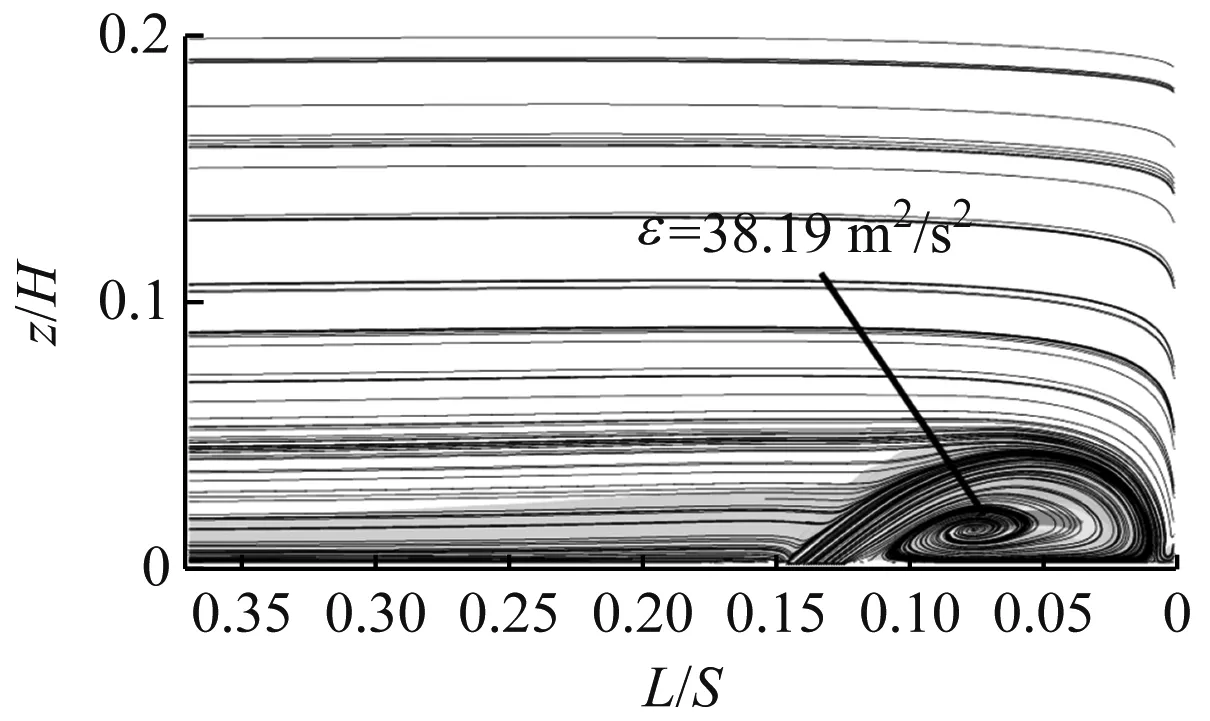
(b) 定常射流模型

(c) t=0.03T

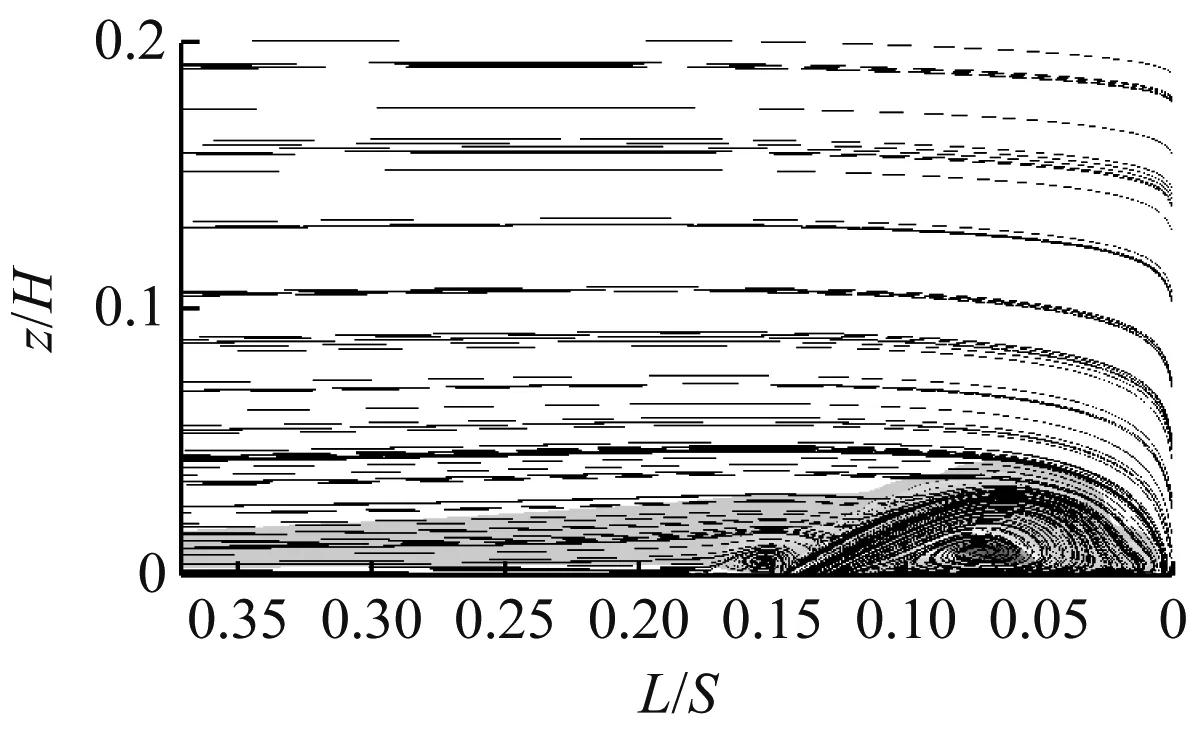
(d) t=0.54T

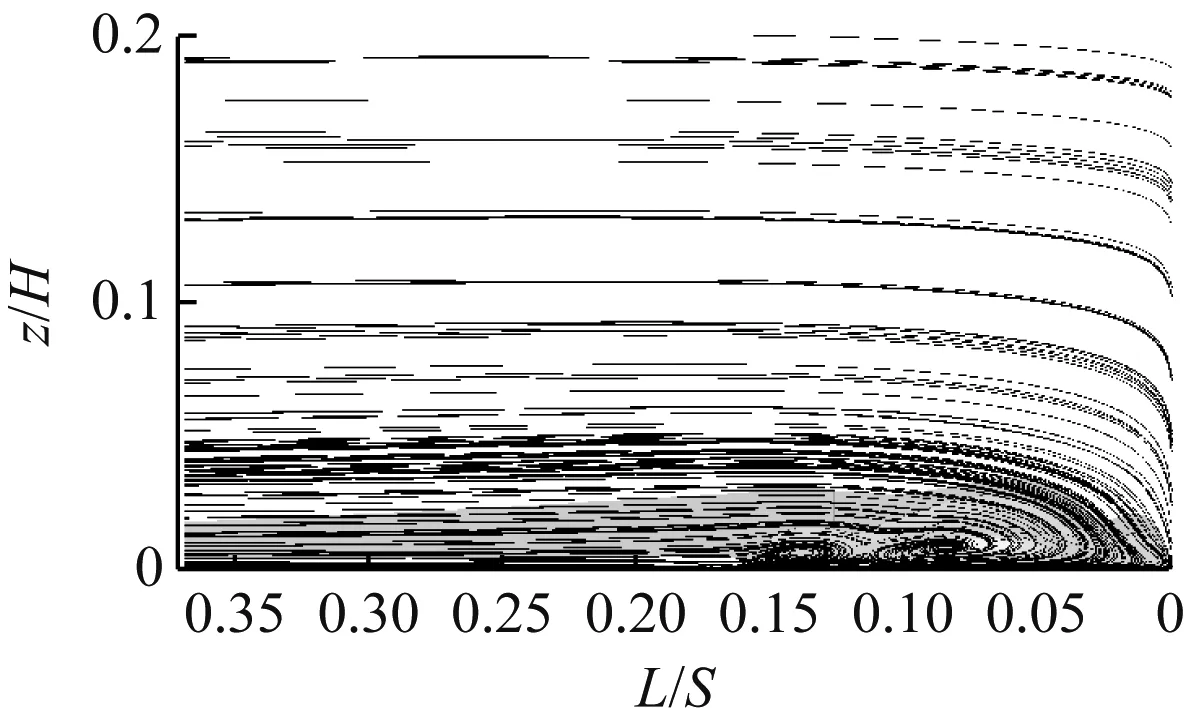
(e) t=0.66T

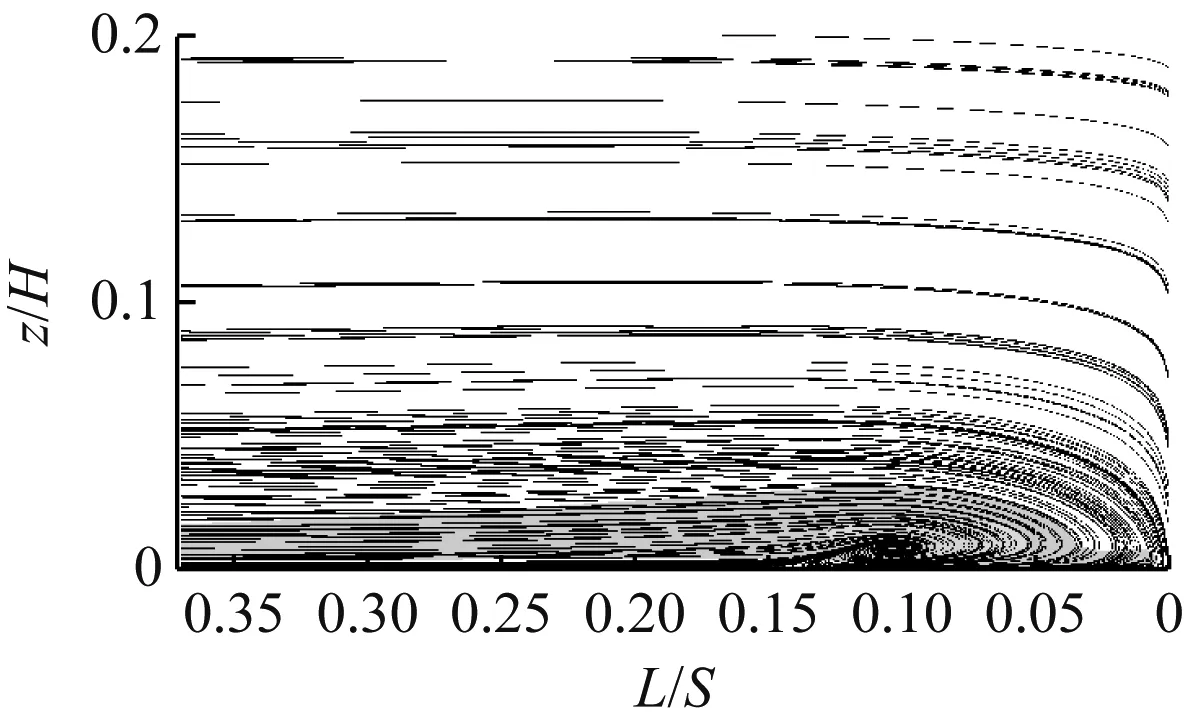
(f) t=0.86T

从图6(f)进入下一循环周期到图6(c)的过程是射流从无到有的过程。由于射流的突然出现，加剧了射流与主流的掺混，使得湍动能有所增强。随着射流与主流掺混，前缘马蹄涡的湍动能在不断增强，如图6(c)和图6(d)所示。可见，射流出现并与主流掺混的发展过程对控制端壁二次流是不利的，射流消失引发的非定常效应对端壁二次流的流动控制起着重要作用。因此，控制射流消失的节点时刻非常重要，也就是要合理选取占空比。

从图4可知，占空比小于0.6时，无射流时间较长，被非定常效应抑制的流动分离现象会再次发生，不利于一个周期内时均总压损失的控制；占空比在0.6～0.8时，由于非定常效应充分发展所需时间约为0.2T(图6(e)到图6(f)的时间)，而后续无射流时间大于0.2T，该非定常效应可在无射流时间段充分发展，因此占空比对时均总压损失并无较大影响。占空比为0.6时，方波函数射流的非定常效应达到最佳状态，一个周期内时均总压损失比定常射流时略低，且射流质量流量仅为定常射流质量流量的60%。

对比图5中出口总压损失系数与图6中前缘马蹄涡的发展过程可知，在一个周期内，出口总压损失先降低后升高，而前缘马蹄涡湍动能强度先增强后减弱，出口的总压损失相对于前缘马蹄涡湍动能存在延迟现象。其原因在于，射流从前缘马蹄涡的流动控制开始，其对叶栅内流动的影响效果是需要时间向后续流场传递的，这是一个动态的发展过程。

3 正弦函数射流

3.1 正弦函数射流参数设计

正弦函数射流的设计中有3个变量：振幅a、无量纲频率F+以及时均动量系数Cμ，正弦函数射流表达式如下：

(10)

(11)

式中：f1为正弦函数周期对应的频率；f为Langston原始叶栅气流从叶栅进口到出口对应的频率。

图7给出了不同工况下的时均总压损失系数分布。黑色点方框为定常射流的工况点，由于其不存在振幅，所以可将其二维图沿a(振幅)坐标轴拉伸扩展为三维空间曲面；图中各离散点为不同射流频率下的总压损失系数分布，在三维空间曲面上方的离散点总压损失较高，在曲面下方的离散点总压损

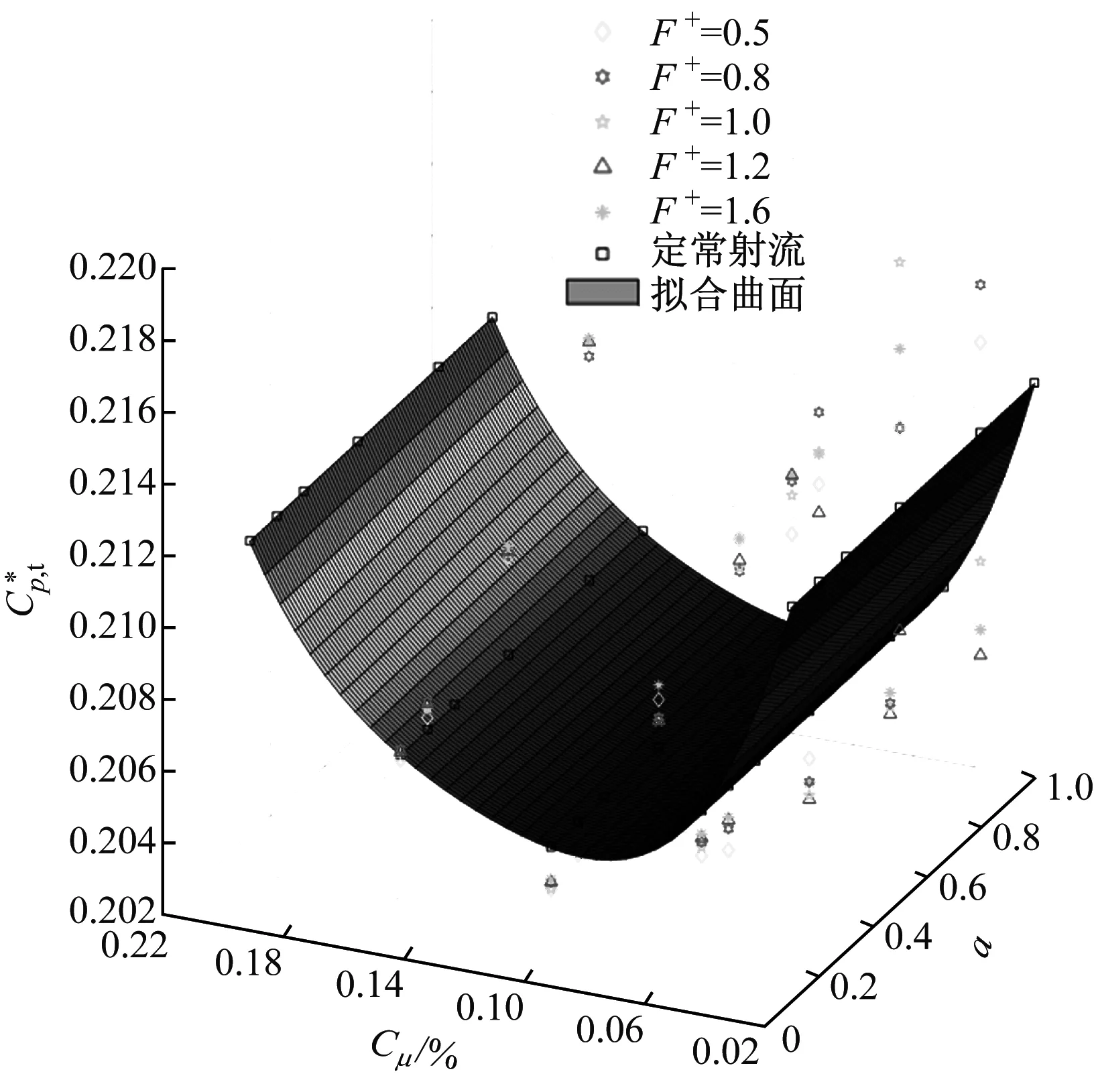
图7 不同工况下时均总压损失系数分布

失较低。

使用Matlab中Thin-plate spline 曲面拟合方式进行数学插值拟合三维空间曲面。另该光滑曲面通过所有的控制点，且其表面总曲率最小。结果如表4所示，其中SE为误差平方和，R2为确定系数。

表4 曲面拟合回归分析

(12)

(13)

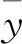
SE越小，R2越接近于1，表明模型拟合效果越好。由以上回归分析可知，在该样本空间下，曲面拟合程度较为精确。

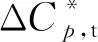
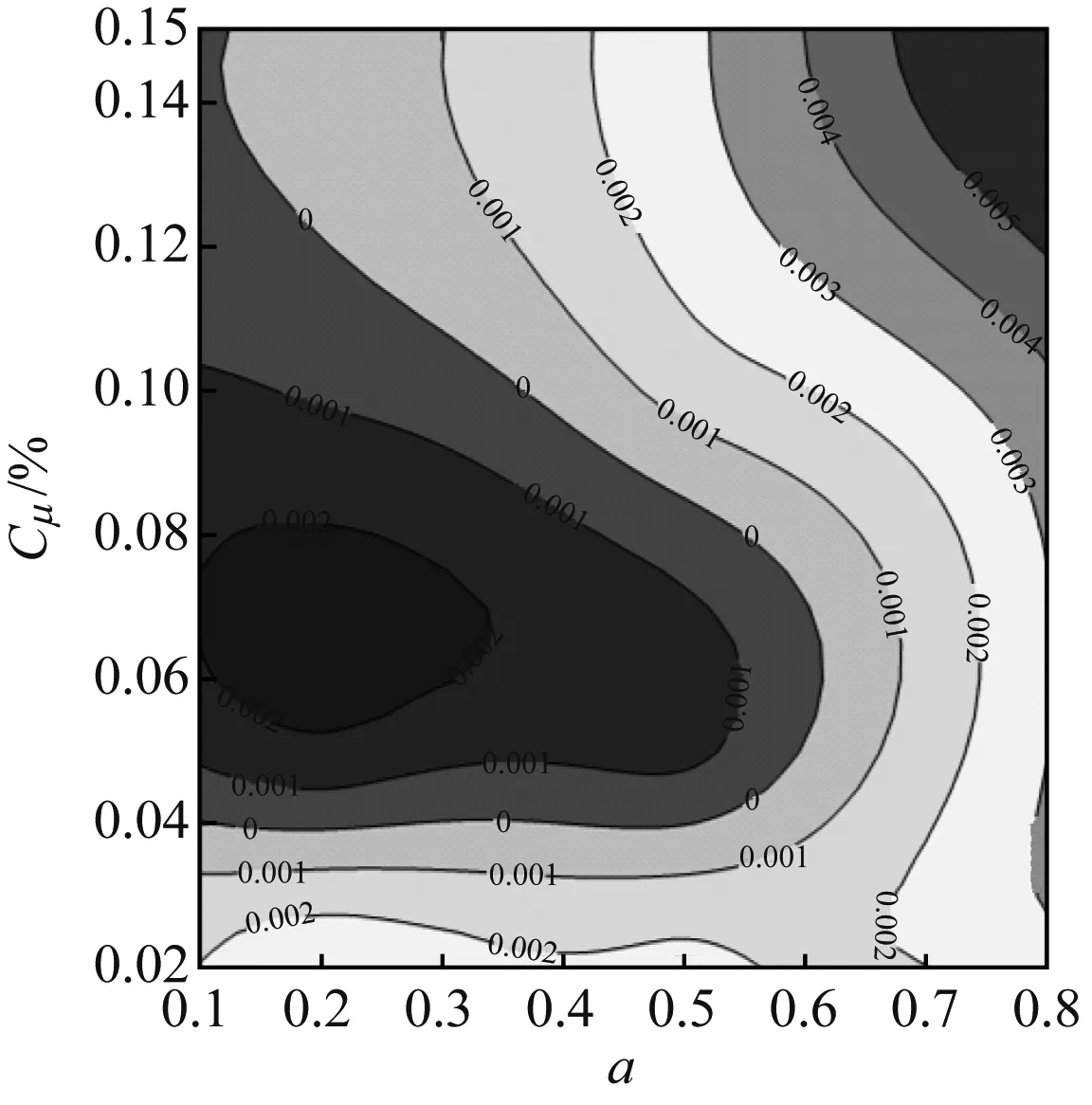
(a) F+=0.5

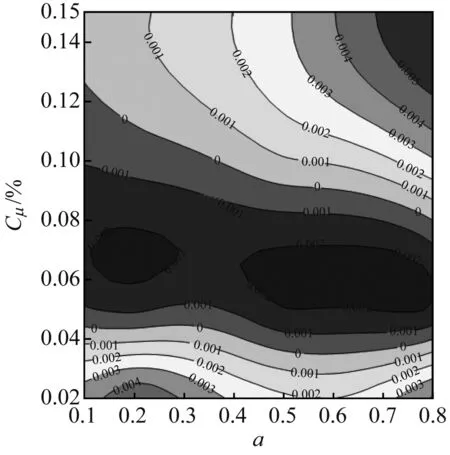
(b) F+=0.8

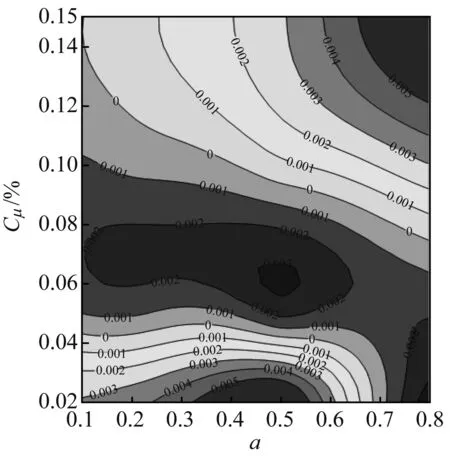
(c) F+=1.0

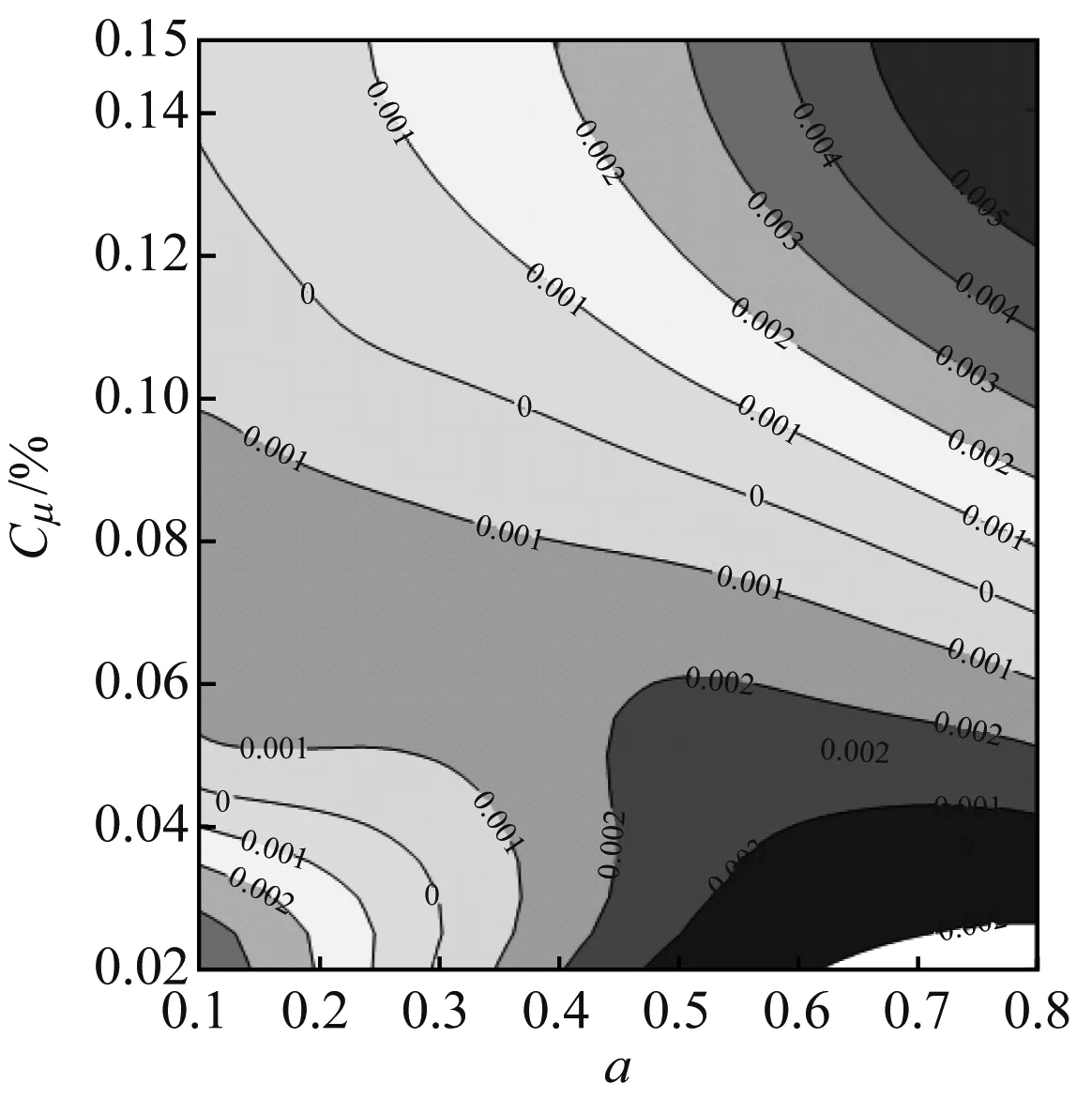
(d) F+=1.2

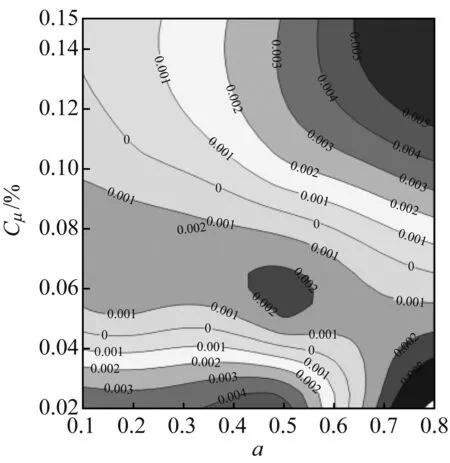
(e) F+=1.6

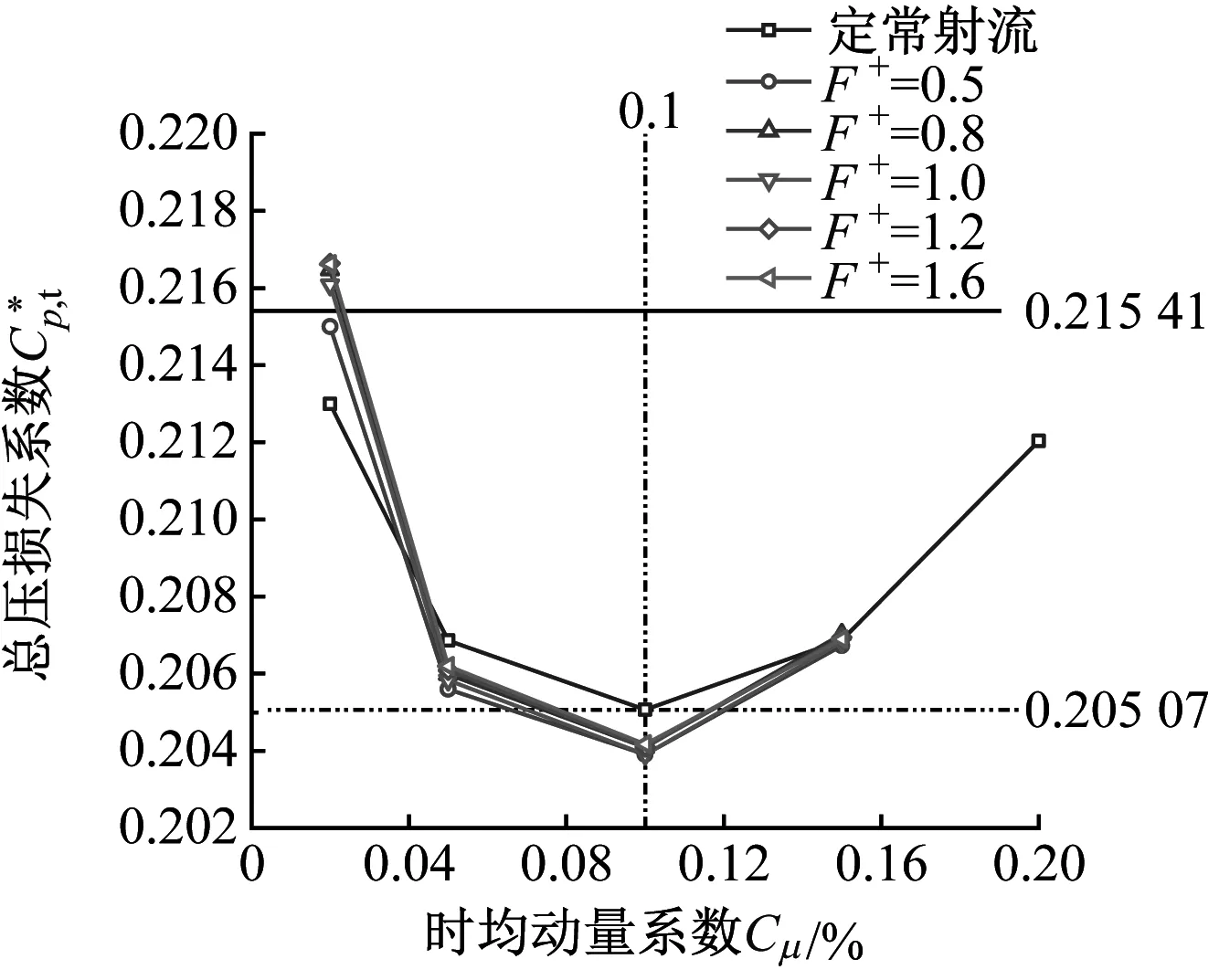
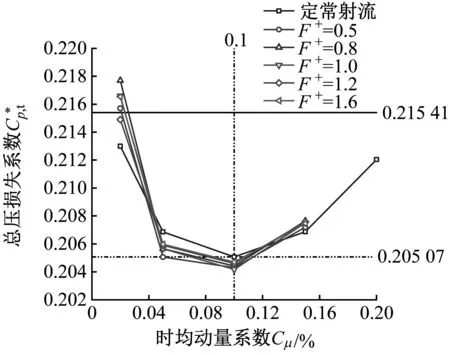
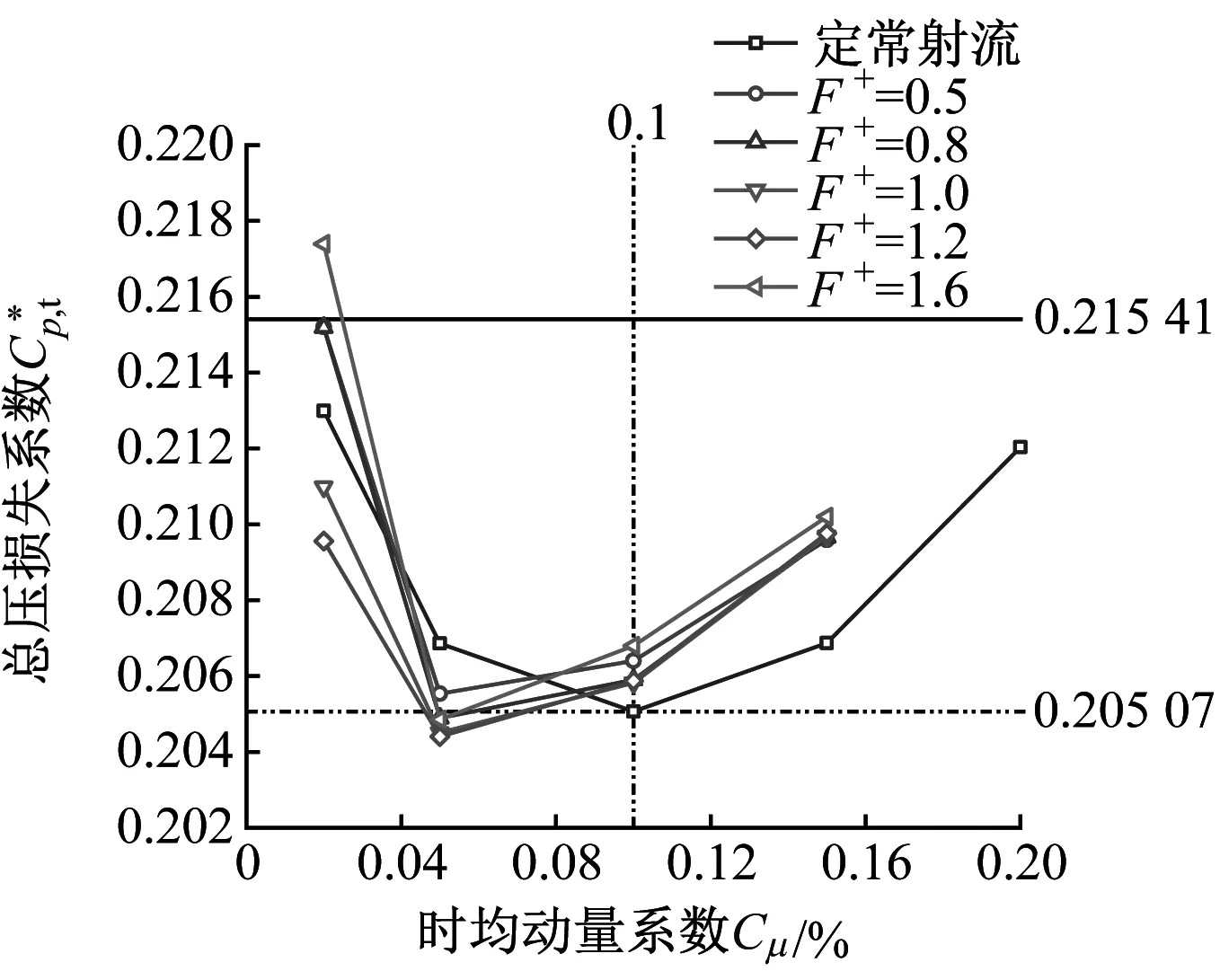
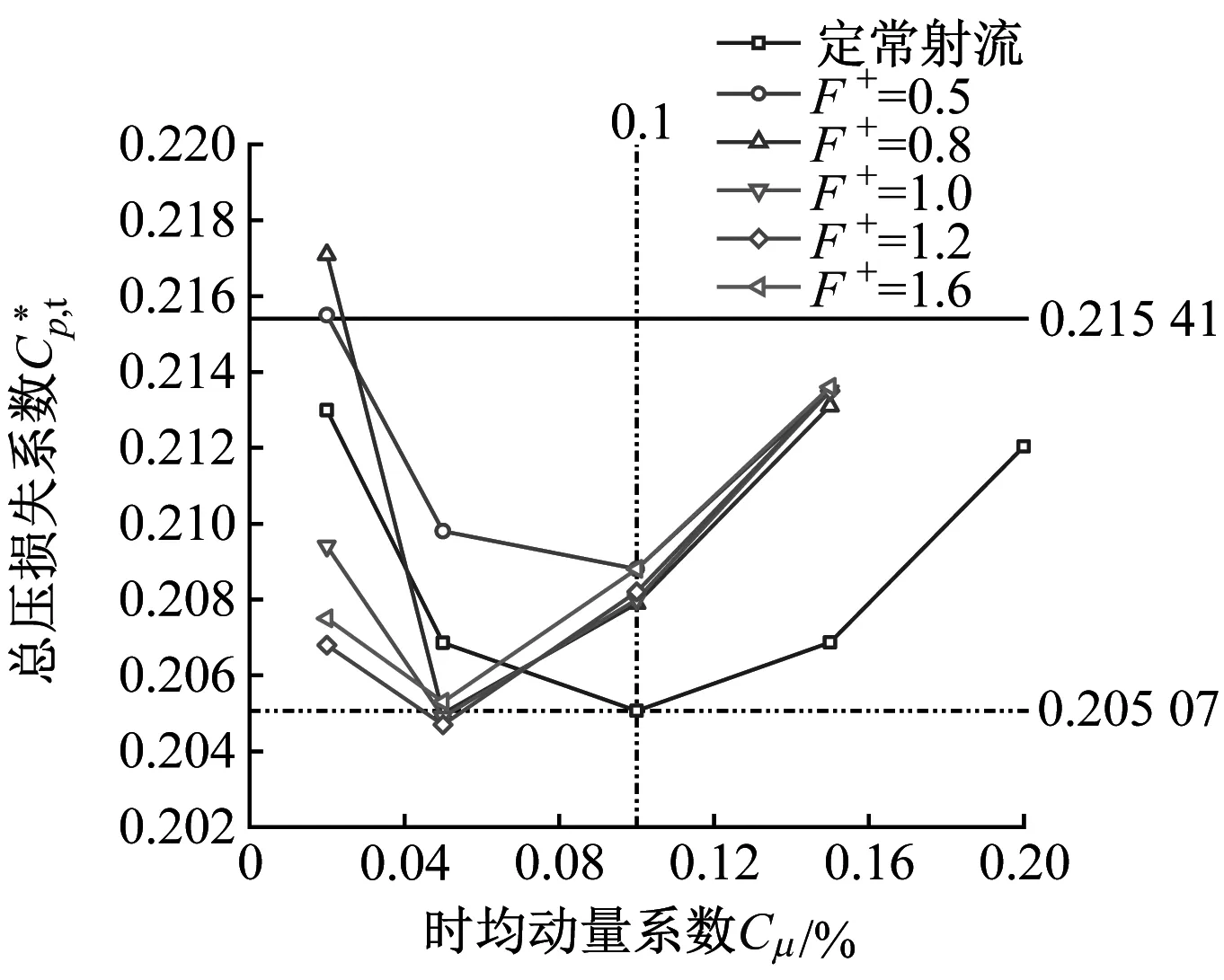
图9给出了不同振幅下，频率与时均动量系数对总压损失的影响规律，其中水平实线为Langston模型的总压损失系数，水平虚线为定常射流孔模型的总压损失系数。从图9可以看出，随着振幅的增大，频率对时均总压损失系数的影响逐渐变大，且不利于总压损失的降低。因此，合理的振幅取值范围应为0.1～0.2。

从图9还可以看出，正弦函数射流对总压损失的减少量相对于Langston原始叶栅较为可观，但与定常射流相比，在最优情况下其总压损失只有0.4%的减少量。因此，在投入射流无法有效降低总压损失的情况下，应考虑减少射流质量流量的投入。

以总压损失系数为0.205 07为参考，该水平虚线与不同工况下的正弦函数射流的交点，即为正弦函数射流减少射流质量流量的合理搭配的工况点。图9中，当振幅为0.2、频率为0.5、时均动量系数为0.05%时，其正弦函数射流的时均总压损失系数恰好能达到0.205 07，此时的正弦函数射流一周期内的射流质量流量仅为定常射流时的70.7%。

3.2 正弦函数射流影响出口总压损失的时域分析

根据3.1节可知，在图9(b)中，振幅为0.2、频率为0.5、时均动量系数为0.05%的正弦函数射流为保持总压损失不变情况下，射流质量流量最少的搭配。振幅为0.2、频率为1.0、时均动量系数为0.10%的正弦函数射流为总压损失最低的搭配。

图10给出了上述2种组合搭配下，正弦函数射流进口速度和透平叶栅出口总压损失系数的时域图。由图10可知，2种搭配下的透平叶栅总压损失系数周期分别为2T和T，这与频率F+=0.5和F+=1.0相匹配。同时当频率F+=1.0时，出口的总压损失系数随时间的变化与射流进口速度随时间的变化保持高度相似；当频率F+=0.5时，由于该射流频率与Langston原始叶栅的频率1/T不匹配，因此出口总压损失系数的时域图比较混乱，但整体上与射流的变化规律相似。虽然频率从0.5改变到1.6，透平叶栅的流动变化规律较差，但是频率F+=0.5时的射流对出口总压损失系数变化幅度的影响小于频率F+=1.0时的射流，这对透平叶栅的流动控制相对有利。

(a) a=0.1

(b) a=0.2

(c) a=0.5

(d) a=0.8

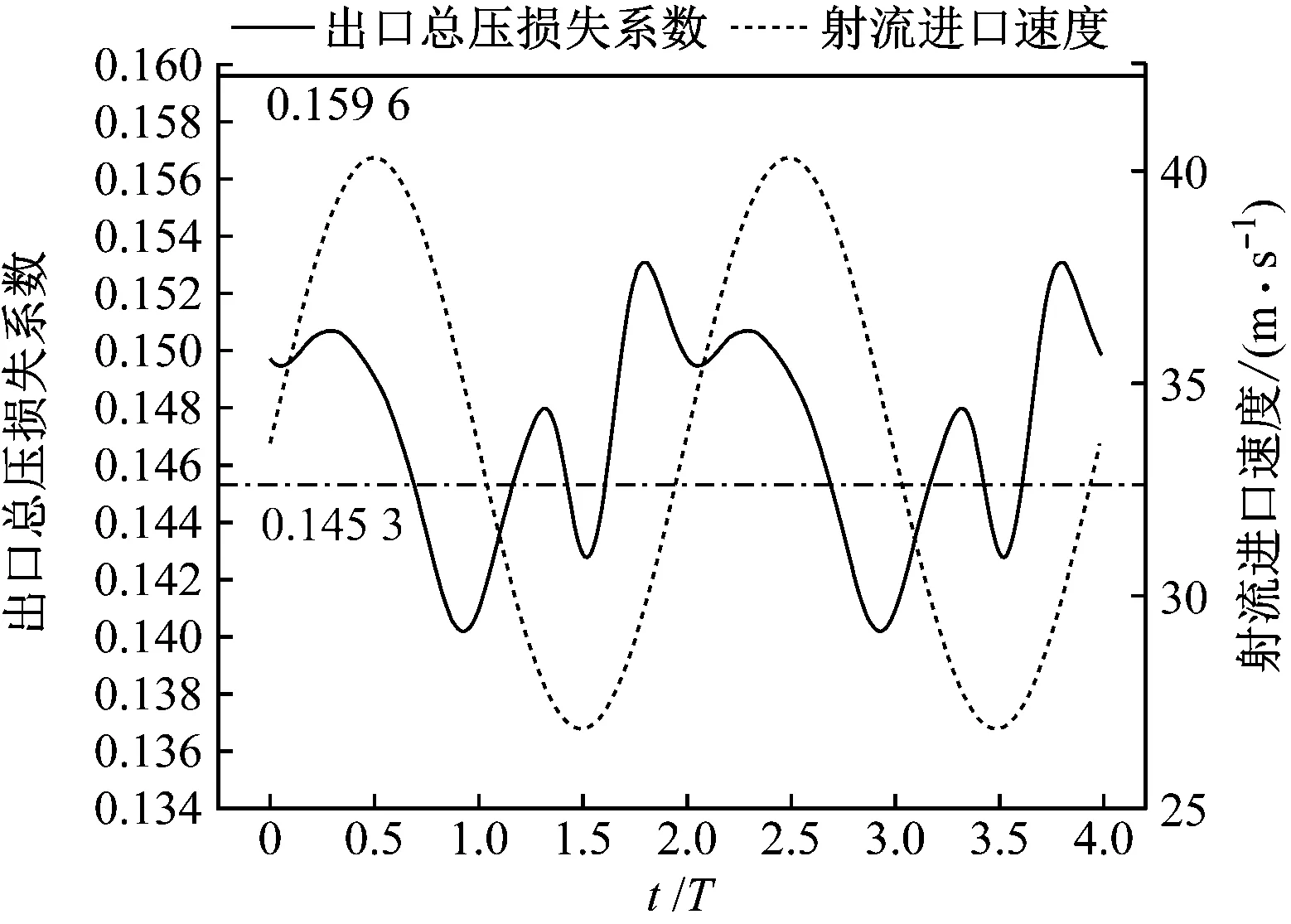
(a) 振幅为0.2、频率为0.5、时均动量系数为0.05%

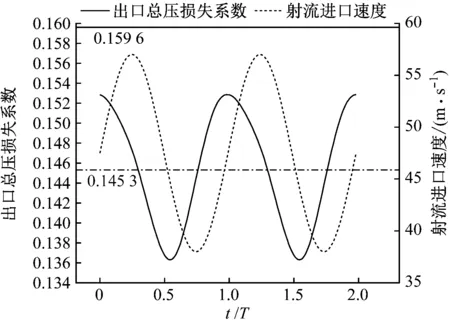
(b) 振幅为0.2、频率为1.0、时均动量系数为0.10%

4 结 论

(1) 方波函数射流中的非定常效应表现为在射流突然消失的时刻，会产生一个低压区，从而很大程度上抑制了前缘马蹄涡的流动分离现象，削弱了其湍动能，进而削弱后续二次流强度。

(2) 方波函数中的占空比在端壁二次流的流动控制中存在重要作用。占空比小于0.6时，无射流时间较长，被非定常效应抑制的流动分离现象会再次发生，不利于一周期内时均总压损失的控制；占空比在0.6～0.8时，由于该非定常效应充分发生所需时间约为0.2T(发生时间较为迅速)，因此占空比对时均总压损失并无较大影响。占空比为0.6时，方波函数射流的非定常效应达到最佳状态，一个周期内时均总压损失比定常射流时略低，且射流质量流量仅为定常射流质量流量的60%。

(3) 通过对正弦函数射流不同振幅、频率、时均动量系数下的时均总压损失系数分析以及与定常射流下的时均总压损失进行差值计算，可得到不同频率下时均动量系数与振幅的合理组合。当振幅为0.2、频率为0.5、时均动量系数为0.05%时，正弦函数射流可达到定常射流总压损失的最低水平，其所需质量流量仅为定常射流质量流量的70.7%。