基于双通道变分自编码器的高光谱图像分类

刘遵雄，石亚鹏，彭潇雨，王毅宏

华东交通大学 信息工程学院，南昌 330013

得益于过去几十年里遥感技术的快速发展，高光谱遥感器通过在数百个连续的窄光谱波段对同一空间区域进行成像，生成高维的高光谱图像数据（HSIs）。高光谱图像为三维立方体结构，由二维空间维度与数十甚至上百个光谱波段组成，在包含丰富的光谱特征的同时具有较高的空间相关性，能够有效地反映成像地物信息，但同时高光谱图像也存在维数灾难、信息冗余、同谱异物、异物同谱和非线性数据空间等问题[1]。高光谱图像增强了对地面物体的识别能力[2-5]，在精准农业[6]、矿产勘探[7]、监视环境[8]和军事领域[9]等领域得到了广泛的应用。高光谱图像分类算法作为这些应用中的一项重要的前提技术，根据图像中的光谱信息和空间信息将图像中的每个像元划分为不同的地物类别[10-11]。

近些年随着高光谱图像的应用越来越广泛，高光谱图像的分类技术作为其重要的信息处理分析手段也愈显得重要，故诸多国内外学者将研究方向转向高光谱图像的分类问题。HSIs分类算法按有无标签训练数据分为三类：监督分类、半监督分类和无监督分类。得益于高光谱遥感技术的高速发展，高光谱图像有了一定数量的已标记数据，使得高光谱图像可以进行有监督训练完成分类。监督分类的方法通过对标签数据的训练，依据经验损失最小化、结构损失最小化等原则进行数据分类。其中最小错误概率的贝叶斯分类器、随机森林、支持向量机（SVM）、基于拉普拉斯算子的SVM都是基于高光谱图像的光谱特征分类的方法，并没有用到空间特征，故分类效果大多不是很理想[12]。2014年Chen等人在高光谱图像分类中首次使用深度学习[13]，他们使用多层叠加的自动编码器提取联合频谱空间特征。2015年Chen等人将深度信念网络用于高光谱图像分类获得了不错的分类效果[14]。2018年Zhu等人将深度卷积生成对抗网络（DCGAN）引入到高光谱图像分类中[15]。近几年来循环神经网络与卷积神经网络被证明在高光谱图像上具有较好的分类性能[16-17]。半监督分类将有限有标签数据与大量无标签数据一起训练进行分类，如基于半监督流形对齐（SSMA）方法[18]、基于主动学习[19]的分类方法。而无监督分类是在无标签数据情况下，利用数据本身同类相似性和类间向异性对数据分类，如Kmeans、遥感人工免疫网络[20]、模糊C-means聚类[21]、稀疏子空间聚类[22]。

变分自编码器（VAE）是一种深度隐空间生成模型的同时也具有特征提取的功能，能够学习输入数据的潜在表示，通过编码器输出潜在变量概率的均值和方差得到分布参数[23]，进而从分布中采样生成隐变量，作为解码器的输入数据，用来重构编码器中原始输入数据。因此可以从解码器的输出中获取重构数据，同时从隐变量中得到数据的特征。在图像领域中，由于VAE生成的图片偏模糊，因此本文更侧重的是VAE作为图像特征提取器的作用。

高光谱图像是由二维空间域和光谱域组成的三维数据体，它们都包含分类的必要信息。针对高光谱图像现有的变分自编码器分类方法没有完全有效利用图像中的光谱和空间信息，存在图像信息丢失问题，提出一种基于双通道变分自编码器的高光谱图像分类算法，提出的深度模型由两个通道组成，改进的一维CVAE分类框架作为光谱通道提取光谱特征，利用卷积神经网络与长短期记忆网络改进CVAE得到的二维CRCVAE分类框架作为空间通道提取空间特征；然后结合以上两种框架形成双通道VAE分类框架，通过该框架将光谱特征和空间特征融合形成空谱联合特征，最后把联合特征送入softmax分类器中进行分类，获得更高的分类精度。

1 变分自编码器

变分自编码器（VAE）是由Kingma等人在2014年提出的基于变分贝叶斯（variation Bayes，VB）推断的一种深度生成模型[24]，目前主要用于特征提取和数据生成。其框架结构如图1所示，由编码器网络和解码器网络组成，其中解码器也叫生成器。编码器对原始输入数据进行变分推断，生成潜在变量概率的均值和方差得到分布参数，称为编码网络；生成器根据编码网络生成的隐变量的概率分布，重构原始数据的近似概率分布，称解码网络或生成网络。

图1 VAE框架结构Fig.1 VAE framework structure

其中，Xi为原始数据；Zi为经编码器qφ编码后的隐变量；Xi′为经解码器pθ重构的数据。

VAE的整体结构与自编码器结构类似，但两者的作用原理大不相同，VAE的编码器输出正态分布参数均值和方差，还要进行重采样操作，而自编码器的编码器输出的是数据深层特征。

VAE网络结构的目标是通过最大化条件概率pθ(Xi|Zi)间接地最大化重构数据的生成概率pθ(Xi)，并且尽可能使得重构数据无限接近于原始数据。由于隐变量Z的分布无法直接观测，不能直接使用EM算法进行变分推断求解，为之VAE用编码网络计算出的条件概率qφ(Zi|Xi)来近似真的后验概率pθ(Zi|Xi)，并假设qφ(Zi|Xi)为一个高斯分布。通过从原始数据到隐变量的条件概率qφ(Zi|Xi)进行N组随机采样得到隐变量并使其与之生成的数据一一对应，采样的目标参数实际上是编码网络生成的均值(μ)和标准差(σ)两个向量。VAE使用KL散度来衡量编码器产生的分布与真实分布的相似度，并通过优化约束参数φ和θ使KL散度最小化，即让两种分布尽可能相似：

其中，lgpθ(Xi)是需要最大化的对数似然函数，假设记：

由公式（3）、（4）得：

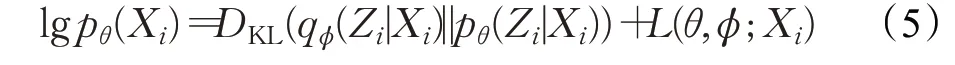
由于KL散度DKL(*)≥0恒成立，当且仅当两个分布相同时取零值，lgpθ(Xi)≥L(θ,φ;Xi)恒成立，故L(θ,φ;Xi)称为对数似然函数lgpθ(Xi)的变分下界。由于直接优化lgpθ(Xi)不可行，VAE可以通过最大化变分下界L(θ,φ;Xi)来间接最大化lgpθ(Xi)。根据联合分布pθ(Xi′,Zi)=pθ(Zi)pθ(Xi′|Zi)，隐变量Zi的先验分布pθ(Zi)可以通过其后验分布pθ(Zi|Xi)进行参数变换使其服从标准正态分布，由于：

其中，pθ(Zi)为标准正态分布，qφ(Zi|Xi)和pθ(Xi|Zi)为一般正态分布，故公式（6）第一项刚好等于：

其中，K表示隐变量的维度。对于公式（6）第二项表示依赖Z重建出来的数据X′要与原始数据X尽可能相似，因此采用自编码器形式的重构误差来做代替：

由于优化目标是要最大化L(θ,φ;Xi)，故最终的优化损失函数为：

特别需要注意的是，由于该网络采用的是随机采样，无法使用反向传播算法优化网络参数，因此使用了“重新参数化”的技巧。首先按照分布ε~N(0,I)对ε进行采样，然后通过变换Zi=μi+σi×εi来获得Zi的采样。至此，优化损失函数的每一项都可以计算得到，模型的结构可以最终确定，VAE详细结构图如图2所示。

图2 VAE详细框架结构Fig.2 VAE detailed framework structure

2 基于双通道VAE的高光谱图像分类算法

2.1 基于一维CVAE分类框架提取光谱特征

本文使用一维条件变分自编码器（CVAE）分类框架提取高光谱图像的光谱特征，网络结构在图3所示CVAE网络基础上改进，调整网络结构参数，使其能提取高光谱图像全部的光谱特征。该算法提取光谱特征无需对高光谱图像进行降维预处理操作，直接将高光谱数据送入框架网络中，避免了数据在预处理过程中的丢失。编码网络提取输入数据的光谱特征并将特征向量输出到隐藏层，光谱特征向量在隐藏层中经过重采样后通过生成网络重构原始输入数据，当生成的数据与原始数据基本一致时网络提取到全部的光谱特征。为了避免神经网络太浅导致网络对复杂特征表示能力差与分类的泛化能力受制约等问题，根据实验效果适当加深了编码网络和生成网络，增强了网络的学习能力，改进后编码网络能提取更复杂更深层次的光谱特征，生成网络生成的数据更加贴近原始数据，从而改进后的网络可提取全部的光谱特征。改进后的1D-CVAE分类与特征提取框架网络由5层全连接编码层、5层全连接生成层、1层隐变量层和1层Softmax多分类层构成。对于含有N个像素点的原高光谱图像，选取其第n(n∈N)个像素点的光谱向量Sn∈RM×1（其中M为光谱带长度）作为1DCVAE框架的输入，从隐变量层的输出中得到一维光谱特征向量f1，包含用于分类的深层光谱特征。

图3 一维CVAE分类结构Fig.3 One-dimensional VAE classification structure

2.2 基于二维CRCVAE分类框架提取空间特征

传统VAE采用深度神经网络（DNN）对参数进行训练、中间隐变量层都为全连接层、KL散度做正则惩罚项，这种结构使得其缺乏表达复杂分布的能力，在处理生成图像时会有生成图像模糊、复杂结构特征表现能力差等缺点，为了克服这些缺点，提取高光谱图像更为全面的空间特征。本文提出基于循环通道条件变分自编码分类框架提取空间特征，该网络结构利用全卷积神经网络代替DNN，使只关注全局特征的网络增强了局部深度细节特征的提取能力，同时在隐变量层中加入了两个长短期记忆网络（LSTM），将时序性结构整合到隐变量层，对隐变量通道进行递归处理，增强从全局到细节局部特征的学习表达能力，加入生成对抗网络结构并使用两种正则化惩罚项代替KL散度正则项，从而能提取高光谱图像更为全面的空间特征。

高光谱图像波段的高维特性导致数据难以处理的同时容易引起Hughes现象，本文使用主成分分析（PCA）对高光谱数据进行降维。由于高光谱波段之间存在较高相关性，PCA可以将原始高光谱图像从数十上百个波段转化为少数几个具有综合性且彼此之间互不相关的波段。PCA降维是通过对已标准化处理过的高光谱图像矩阵计算出协方差矩阵，进而计算出协方差矩阵每一列的特征向量与特征值，按每一特征值与所有特征值之和的比例由大到小排序，当前m个比例值之和即累计贡献率大于给定的阈值时，选取前m个主成分代替原高光谱图像。如选取的主成分个数小于m时，会丢失一部分图像信息，选取的主成分个数大于m时，为了极少一部分图像信息会增加大量运算成本。本文累计贡献率阈值设置为0.99，此时高光谱图像被降维成三维。将图像切割成大小为45×45×3的数据块，选取高光谱图像中与1D-CVAE框架网络的输入像素所相对应的空间邻域块Pn∈R45×45×3作为2D-CRCVAE框架网络的输入进行特征提取，从隐变量层的输出中得到空间特征向量f2，包含用于分类的深层空间特征。

改进的2D-CRCVAE空间特征提取算法的分类框架结构如图4所示，由编码网络、生成网络、隐变量层和一个Softmax分类器组成。其中编码网络包含5层卷积层和1层全连接层，生成网络包含5层反卷积层和1层全连接层，隐变量层含有两个LSTM模块。LSTM模块结构如图5所示，第一个LSTM模块中，将编码网络的输出σ按顺序输入LSTM中，输出的σL作为近似后验的方差。将采样得到的样本z通过另一个LSTM模块得到更复杂的表示u，这两个LSTM层可以提升网络结构的分类性能。

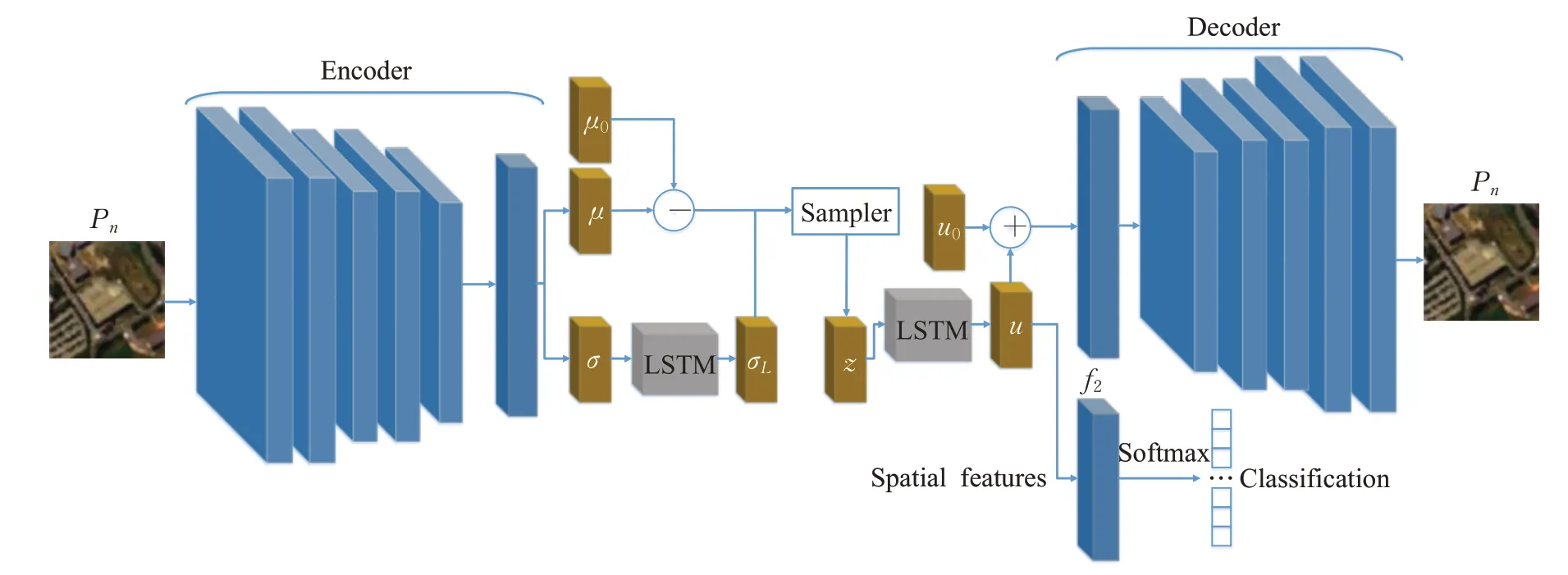
图4 二维CRCVAE分类结构Fig.4 Two-dimensional CRCVAE classification structure

图5 LSTM框架结构Fig.5 LSTM framework structure

2.3 双通道VAE分类框架设计

高光谱图像不仅包含光谱特征，还包含空间特征，基于空谱联合特征的分类方法往往比基于单一特征的分类方法更有效[25]。为了提取高光谱图像更为完整的光谱空间特征，本文在上述光谱和空间特征提取框架的基础上，以空谱特征联合为中心思想，设计如图6所示的双通道VAE分类模型。首先通过训练1D-CVAE框架提取光谱特征f1，再通过训练2D-CRCVAE框架提取空间特征f2，最后将两种特征融合生成空谱联合特征f，并将空谱联合特征f送入softmax多元回归分类器中进行分类。将高光谱图像数据分解为光谱数据与空间数据，分别作为光谱通道与空间通道的输入数据，采用随机梯度下降算法（SGD）对网络进行训练，输入softmax层的空谱联合特征包含了几乎全部高光谱图像用于分类的特征信息，保证了双通道VAE分类网络具有高分类精度的性能，通过softmax多元回归分类器得到高光谱图像的分类结果，相对于基于光谱特征或空间特征的方法具有更高的分类精度。

图6 双通道VAE分类框架结构Fig.6 Two-channel VAE classification framework structure

本文采用求和融合的方式构造融合特征网络，求和融合是一种简单且高效的特征融合方法，通过将维度相同的光谱特征f1与空间特征f2中对应值一一相加得到空谱联合特征向量，运算方便且只增加少量运算成本。空谱联合特征f的表达式为：

3 实验结果及分析

为了验证本文所提出算法在高光谱图像分类任务上的有效性，选取了Indian pines、Pavia University数据集这两种常用高光谱数据集作为实验数据进行评估。并将本文所提出的双通道VAE分类算法（TC-VAE）与近些年来所提出的高光谱分类算法进行比较验证模型性能，SVM算法为传统的高光谱分类研究方法，本文将其作为对比的基准，1D-CNN算法仅使用高光谱图像光谱特征进行分类，2D-CNN算法仅使用高光谱图像空间特征进行分类，和3D-CNN算法将高光谱图像的光谱特征与空间特征作为一个整体输入网络进行分类。

在本文提出的1D-CVAE分类框架中，batchsize设置为100，网络的迭代次数为2 000，初始学习率设置为0.001，经500次迭代后学习率变化为0.000 1。在2DCRCVAE分类框架中，编码网络卷积层中第一个卷积核为5×5，其余卷积核为3×3，生成网络反卷积层中最后一个卷积核为5×5，其余卷积核为3×3，batchsize设置为50，网络的迭代次数为2 000，初始学习率设置为0.001，经500次迭代后学习率改为0.000 1。在TC-VAE分类框架中，batchsize设置为50，网络的迭代次数为2 000，初始学习率设置为0.001，经500次迭代后学习率改为0.000 1，都采用随机梯度下降算法（SGD）对网络进行训练。为了验证本文算法在小规模样本数据集上的有效性及泛化能力，对每个数据集中每个地物类别选取10%样本作为训练集，其余90%作为测试集。通过实验测试本文提出算法的分类性能，运行20次取实验结果的平均值作为最终结果。

采用常用的高光谱分类衡量指标总分类精度（OA）、平均分类精度（AA）和Kappa系数来评估所提出算法的性能。

总分类精度表示被正确分类的测试样本数在全部测试样本数中的比率，平均分类精度表示每一个类别分类精度的平均值，Kappa系数表示测试样本的分类预测类别与实际类别的一致性检测指标系数。具体计算公式如下：

其中，K表示类别数；N表示测试样本总个数；P(i,i)表示第i类被正确分类；OA(i)表示第i类的总分类精度；P(i,)(,i)分别表示第i行和第i列的总测试样本数。

3.1 Indian pines数据集实验结果

Indian pines数据集是由机载可视红外成像光谱仪（AVIRIS）于1992年在美国印第安纳州西北部的印度松树测试场地上收集的，其波长范围在0.4~2.5μm，光谱分辨率为10μm，空间分辨率为20 m，图像大小为145 pixel×145 pixel。原始数据集包含220个光谱波段，除去水汽吸收带和低信噪比的波段，剩余200个可用波段作为实验数据。图7显示了Indian pines高光谱伪彩色合成图和真值图。数据集有16种地物类别共计样本10 249个，样本具体分布如表1所示。

表1 Indian pines数据集样本表Table 1 Indian pines dataset sample table

图7 Indian pines伪彩色合成图与真值图Fig.7 Indian pines pseudo color composite map and ground truth map

表2给出了SVM、1D-CNN、2D-CNN、3D-CNN算法和本文提出的算法在Indian pines数据集上的分类性能比较。根据表2中的数据显示，本文提出的双通道VAE分类算法（TC-VAE）在Indian pines数据集上取得最高的的分类精度。总分类精度达到了99.23%，平均分类精度达到了98.48%，Kappa系数为99.12%。相比对比算法中最高分类精度的3D-CNN算法，TC-VAE算法在OA、AA和Kappa系数分别提升了3.82、4.27和4.58个百分点，从分类精度角度TC-VAE分类算法分类效果最优。

表2 各算法Indian pines数据集分类性能比较Table 2 Comparison of classification performances of different algorithms on Indian pines dataset %

图8给出了5种算法在Indian pines数据集上的图像分类对照图，由图可看出，本文算法分类结果错分的点比3D-CNN还要少不少，更为接近Indian pines数据集真值图，可知TC-VAE分类算法分类结果从视觉角度效果最优。

图8 各算法在Indian pines数据集的分类对照图Fig.8 Classification map of different algorithms on Indian pines dataset

3.2 Pavia University数据集实验结果

Pavia University数据集是由机载反射光学光谱成像仪（ROSIS）于2003年在意大利帕维亚大学采集得到，其波长范围在0.43~0.86μm，空间分辨率为1.3 m，图像大小为610 pixel×340 pixel。原始数据集包含115个光谱波段，去除其中带有噪声的波段，剩余103个可用波段作为实验数据。图9显示了Pavia University高光谱伪彩色合成图和真值图。数据集共有9种地物类别共计样本42 776个，样本具体分布如表3所示。

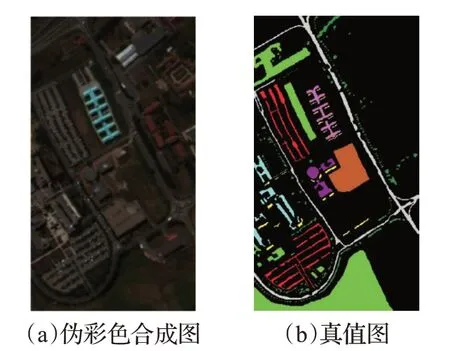
图9 Pavia University伪彩色合成图与真值图Fig.9 Pavia University pseudo color composite map and ground truth map

表3 Pavia University数据集样本表Table 3 Pavia University dataset sample table

表4给出了SVM、1D-CNN、2D-CNN、3D-CNN算法和本文提出的算法在Pavia University数据集上的分类性能比较。根据表4中的数据显示，本文提出的双通道VAE分类算法（TC-VAE）在Pavia University数据集上取得最高的分类精度。总分类精度达到了98.63%，平均分类精度达到了97.49%，Kappa系数为98.43%。相比对比算法中最高分类精度的3D-CNN算法，TC-VAE算法在OA、AA和Kappa系数分别提升了3.40、2.75和3.57个百分点，从分类精度角度TC-VAE分类算法分类效果最优。

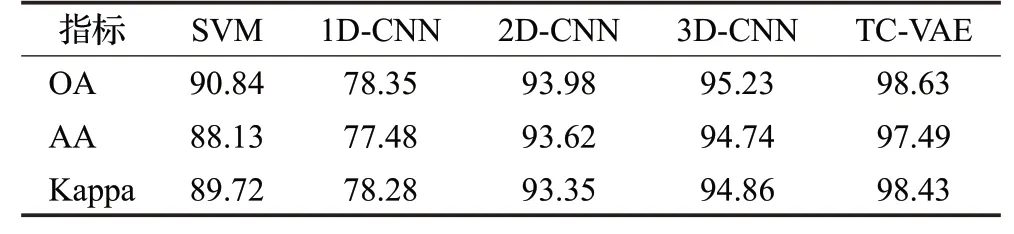
表4 各算法Pavia University数据集分类性能比较Table 4 Comparison of classification performances of different algorithms on Pavia University dataset %

图10给出了5种算法在Pavia University数据集上的图像分类对照图，由图可看出，本文算法分类结果错分的点比3D-CNN还要少不少，更为接近Pavia University数据集真值图，可知TC-VAE分类算法分类结果从视觉角度效果最优。

图10 各算法在Pavia University数据集分类对照图Fig.10 Classification map of different algorithms on Pavia University dataset

4 结论

本文提出了一种基于双通道VAE的高光谱图像深度学习分类算法，该方法可以全面地提取高光谱图像的空谱联合特征提升分类精度。算法由三部分构成，首先基于一维改进CVAE分类框架提取全面的光谱特征，其次基于二维改进CRCVAE分类框架提取完整的空间特征，最后结合上述两种框架构建双通道VAE分类框架，该框架可以将提取到的光谱特征和空间特征融合为空谱联合特征进行高光谱图像分类。实验结果表明，本文算法与传统的SVM算法、1D-CNN算法、2D-CNN算法和3D-CNN算法相比，本文算法获得更高的分类精度与更为平滑的分类结果图。并且本文算法与对比算法中分类精度最高的3D-CNN算法相比在Indian pines数据集上OA、AA和Kappa系数分别提升了3.82、4.27和4.58个百分点，在Pavia University数据集上分别提升了3.40、2.75和3.57个百分点。证明了本文算法对小样本训练的有效性，同时验证了本文算法的先进性和有效性。