基于核心素养下的教学设计
——椭圆及其标准方程第二课时
2022-01-25刘锦贵广东省阳江市第一中学广东阳江529500
刘锦贵(广东省阳江市第一中学,广东 阳江 529500)
一、内容和内容解析
本节课内容是新人教A 版选择性必修第一册第三章第一节《椭圆》.在学习这部分内容之前,我们学习了椭圆的定义及其标准方程,并且学习了使用定义及待定系数法求椭圆的标准方程,在曲线与方程中学习了直译法求轨迹方程.本节课作为椭圆标准方程的第2 课时,重在处理课本108页例题2 与例题3,从中得到形成椭圆的另一些方法,并从例题2 与例题3 中体会椭圆与圆之间的关系.
二、目标和目标解析
1.加深椭圆概念的理解,进一步探讨生成椭圆的方法.
2.通过几何直观想象感受椭圆与圆之间的关系.
三、教学问题诊断分析
1.学生在初中时学习了直径所对的圆周角是直角,垂径定理,需要引导学生将这些学过的内容与高中必修二中垂直与斜率相乘等于-1 联系起来.
2.学生刚刚学习椭圆,对椭圆的概念及其标准方程掌握得还不够深入,求轨迹方程的方法思路还有待加强.
3.在探究圆与椭圆之间的关系时,较为抽象,需借助多媒体辅助教学.
四、教学支持条件分析
学校教室已安装西沃一体机,实物投影仪,几何画板.
五、教学过程设计
(一)复习回顾
1.定义:我们把平面内与两个定点F1,F2的距离的和等于常数(大于|F1F2|)的点的轨迹叫作椭圆.|PF1|+|PF2|=2a(2a>|F1F2|).
2.标准方程.
焦点在x轴:;
焦点在y轴:.
巩固练习:已知点B(-3,0),C(3,0),且△ABC的周长为16,求顶点A的轨迹方程.
解:设点A的坐标为(x,y).
因为|AB|+|AC|+|BC|=16,
所以|AB|+|AC|=10>|BC|.
由椭圆定义知点A的轨迹是椭圆,根据椭圆定义及标准方程可知2a=10,c=3.
所以b2=a2-c2=16,
所以顶点A的轨迹方程是.
设计意图:帮助学生回顾椭圆的定义及标准方程,回顾求轨迹方程的一般思路,为接下来的内容提供基础.
(二)学习新知
例1如图1,在圆x2+y2=4 上任取一点P,过点P作x轴的垂线段PD,D为垂足,当点P在圆上运动时,线段PD的中点M的轨迹是什么?为什么?

图1
解:设点M的坐标为(x,y),点P的坐标为(x0,y0),

因为点P(x0,y0)在圆x2+y2=4 上,
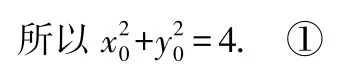
把x0=x,y0=2y代入①得x2+4y2=4,即.
所以点M的轨迹是椭圆.
练习1:(课本115 页第9 题)如图2,DP⊥x轴,D为垂足,点M在DP的延长线上,且,当点P在圆x2+y2=4 上运动时,求点M的轨迹方程,并说明轨迹形状.

图2
解:设点M的坐标为(x,y),点P的坐标为(x0,y0),

因为点P(x0,y0)在圆x2+y2=4 上,

所以点M的轨迹是一个椭圆.
师生活动:
提出问题:从例1 中你能发现圆与椭圆之间的关系吗?
学生回答:椭圆可以由圆压缩得到.
从而得出形成椭圆的一个方法.
进一步提问1-1:回想一下有关圆的知识,你能想到什么?
学生回答:圆的定义,半径,对称,直径所对的圆周角是直角,垂径定理……
进一步提问1-2:回想必修二斜率知识,直径所对的圆周角是直角,与斜率有什么关系?
学生回答:斜率相乘等于-1.
利用几何画板演示给学生看,如图3 所示,让学生观察几何画板的动态演示.

图3
进一步提问1-3:我们通过几何画板演示可以看到圆上的动点P满足kAP×kBP=-1,椭圆里面是否存在类似的结论呢?
学生回答:kAM×kBM=-0.25,为负常数.
进一步提问1-4:是否到两个定点的斜率之积为一个负常数的动点的轨迹就是椭圆,请看例题3.
设计意图:让学生从直观想象中观察出圆与椭圆之间的关系,培养学生直观想象的学科素养,为接下来例题2 的引出做好了铺垫.
例2 如图4 所示,设点A,B的坐标分别为(-5,0),(5,0).直线AM,BM相交于点M,且它们的斜率之积是-,求点M的轨迹方程.
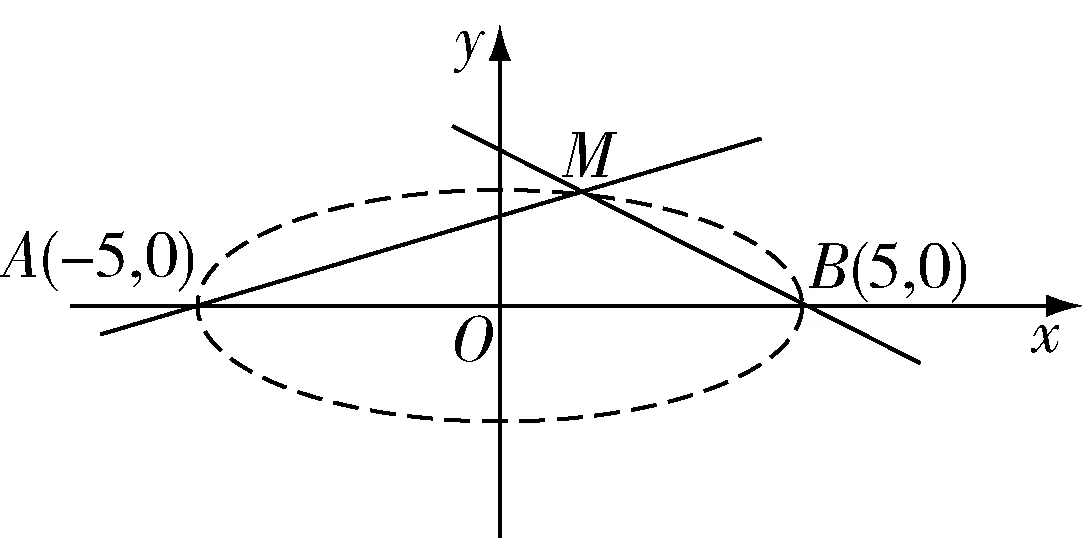
图4
解:设点M的坐标为(x,y),

解:设点M的坐标为(x,y),则,
化简得点M的轨迹方程为.
当t>0 时,点M的轨迹是一条神秘曲线;
当t=-1 时,点M的轨迹是圆;
当t<0 且t≠-1 时,点M的轨迹是椭圆.
师生活动:
提问:你能得出什么结论呢?
学生回答:一个动点到两个定点连线的斜率之积是一个负常数(不等于-1)的轨迹为椭圆,但要注意去掉不符合的两个点.
进一步提问:这个负常数t是否具备什么特点?
设计意图:让学生认识到椭圆还有其他产生方式,感受椭圆蕴含着丰富的、奇妙的性质,促使学生掌握坐标法、数形结合的数学思想方法,并由浅入深,一步一步得到一些新的结论,为接下来的拓展做铺垫.
(三)拓展思考
思考1:已知点A,B的坐标分别为(-a,0),(a,0),M是椭圆(a>b>0)异于A,B的一点,直线AM,BM的斜率之积是否为定值?如是,求出定值;反之,说明理由.
所以直线AM,BM的斜率之积为定值.
得出一个结论:直线AM,BM的斜率之积为定值.

思考2:已知A,B是椭圆=1(a>b>0)上关于原点对称的两点,M是椭圆上异于A,B的一个动点,直线AM,BM的斜率都存在,且kAM·kBM≠0,请问:直线AM,BM的斜率之积是否还为定值?如是,求出定值;反之,说明理由.
解:设点M的坐标为(x,y),点A的坐标为(x1,y1),点B的坐标为(-x1,-y1),

所以直线AM,BM的斜率之积为定值.
得出一个结论:直线AM,BM的斜率之积为定值-.
拓展练习2:已知P是椭圆=1(0<m<4)上任意一点,M,N是椭圆上关于坐标原点对称的两点,且直线PM,PN的斜率分别为k1,k2(k1k2≠0),若|k1|+|k2|的最小值为1,则椭圆E的方程为_________________________.

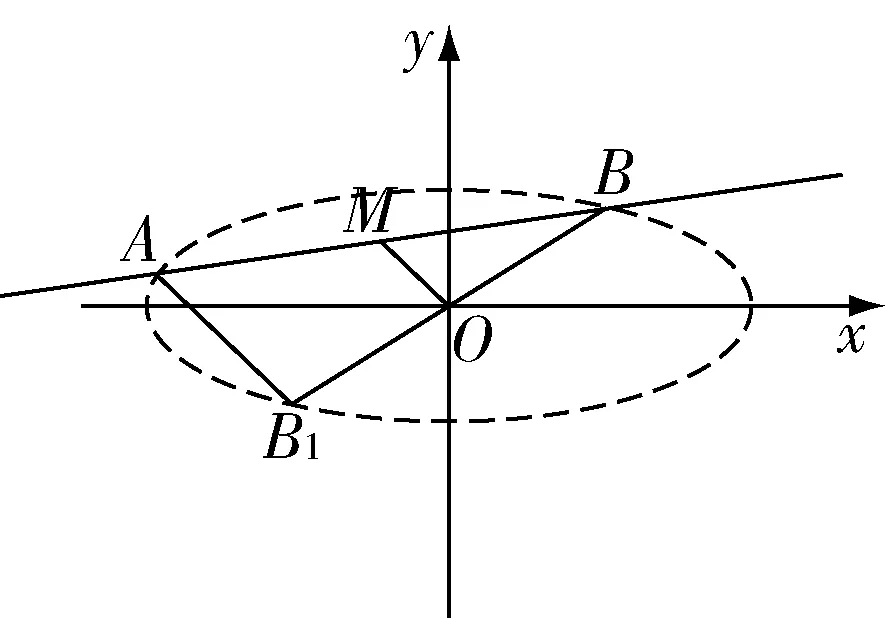
图5
解:连接BO并延长交椭圆于点B1,连接AB1,
因为M,O分别是AB,BB1的中点,
所以OM∥AB1,即kOM=kAB1,


设计意图:进一步体会圆与椭圆之间的关系,并形成一些相关的结论,为以后更好地学习有关椭圆的性质奠定基础.
六、教学反思
本节课由例题2 和例题3 得到形成椭圆的另外一些方法,并从得到这些方法的过程中,体会圆与椭圆之间的关系;同时,将圆中的有关结论推广到椭圆中,得到有关椭圆的一些结论,并将得到的结论应用于解题中.在教学的过程中,教师应充分利用多媒体软件辅助教学,让学生更好地直观想象、感受圆与椭圆的关系.
