分数阶Klein-Gordon-Zakharov方程新的保能量格式

王昌琳，刘 莹，孙建强

（海南大学理学院，海南 海口 570228）

在等离子体物理学中，Zakharov方程是描述等离子体中Langmuir波和离子声波相互作用的经典偏微分方程模型［1］.经典Zakharov方程模型系统也被认为是描述高频兰缪尔波与低频离子的最佳系统模型，其中包括Klein-Gordon-Zakharov方程模型.Klein-Gordon-Zakharov（KGZ）方程是由2个函数u(x，t)和m(x，t)相互耦合的方程.u(x，t)函数表示由电子引起的电场的快速时标分量，描述偏差平衡时离子密度的变化的一类复数函数，m(x，t)是一个实函数.KGZ方程模型类似于Zakharov方程Klein-Gordon Schrodinger方程［2-4］.非线性的Klein-Gordon-Zakharov方程在等离子体物理学中起着重要作用.

近年来，许多学者分析了Klein-Gordon-Zakharov方程解的存在性条件并用数值方法计算方程解的行为.Liu等［4］分析了耦合非线Klein-Gordon方程的周期解.Zhang等［5］分析了Klein-Gordon-Zakharov方程整体解的光滑条件.Tsutaya［6］分析了Klein-Gordon-Zakharov方程小振幅解的整体存在性.同时Wang等［7］和Chen等［8］利用数值方法分析了Klein-Gordon-Zakharov方程数值解的特性.构造分数阶偏微分方程的能量守恒格式在数值模拟能量守恒分数阶偏微分方程中具有重要的意义.Rome等［9］和Hendy等［10］构造了分数阶Klein-Gordon-Zakharov方程的守恒数值格式，并分析了方程的数值行为和守恒特性.

保结构算法在求解具有守恒特性的偏微分方程中具有重要的优势，如保偏微分方程多辛守恒的多Runge-Kutta方法，多辛谱方法等具有长时间的精确计算能力和近似保方程的能量守恒特性［11-12］.保哈密尔顿系统和多辛结构偏微分方程能量守恒的平均向量场方法和保哈密尔顿系统能量守恒的边界值方法［13-15］.利用平均向量场方法和拟谱方法求解如下的分数阶Klein-Gordon-Zakharov方程［9］.

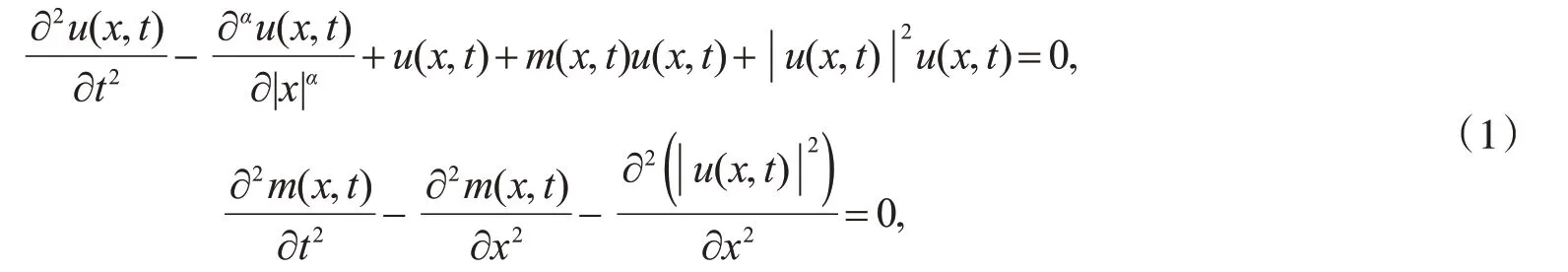
其中，u=u(x，t)=ξ(x，t)+iη(x，t)=ξ+iη，v x=m t.方程（1）具有能量守恒特性.在空间有限域Ω=(a，b)内相应的能量函数为

1 分数阶Klein-Gordon-Zakharov方程的多辛格式

对于分数阶KGZ方程（1），令w(x，t)=u t(x，t)，v x(x，t)=m t(x，t)，v(x，t)=-2p x(x，t)和w=γ+iβ，u=ζ+iη，则方程（1）等价于

方程（4）可以写成如下多辛结构形式

其中，

矩阵分别为

格式（5）满足多辛守恒定律

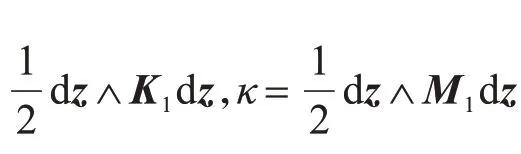
2 分数阶Klein-Gordon-Zakharov方程的多辛保能量方法

令u N(x)表示函数u(x)中的插值逼近I N u(x)，有

则由等式（8）和等式（9）可得

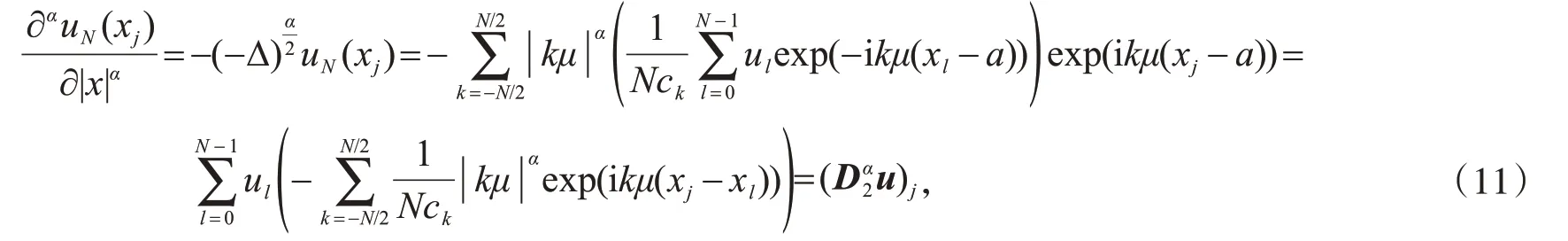
同时对方程中变量p，v关于x的偏导数，相应的谱微分矩阵D1为

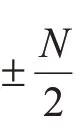
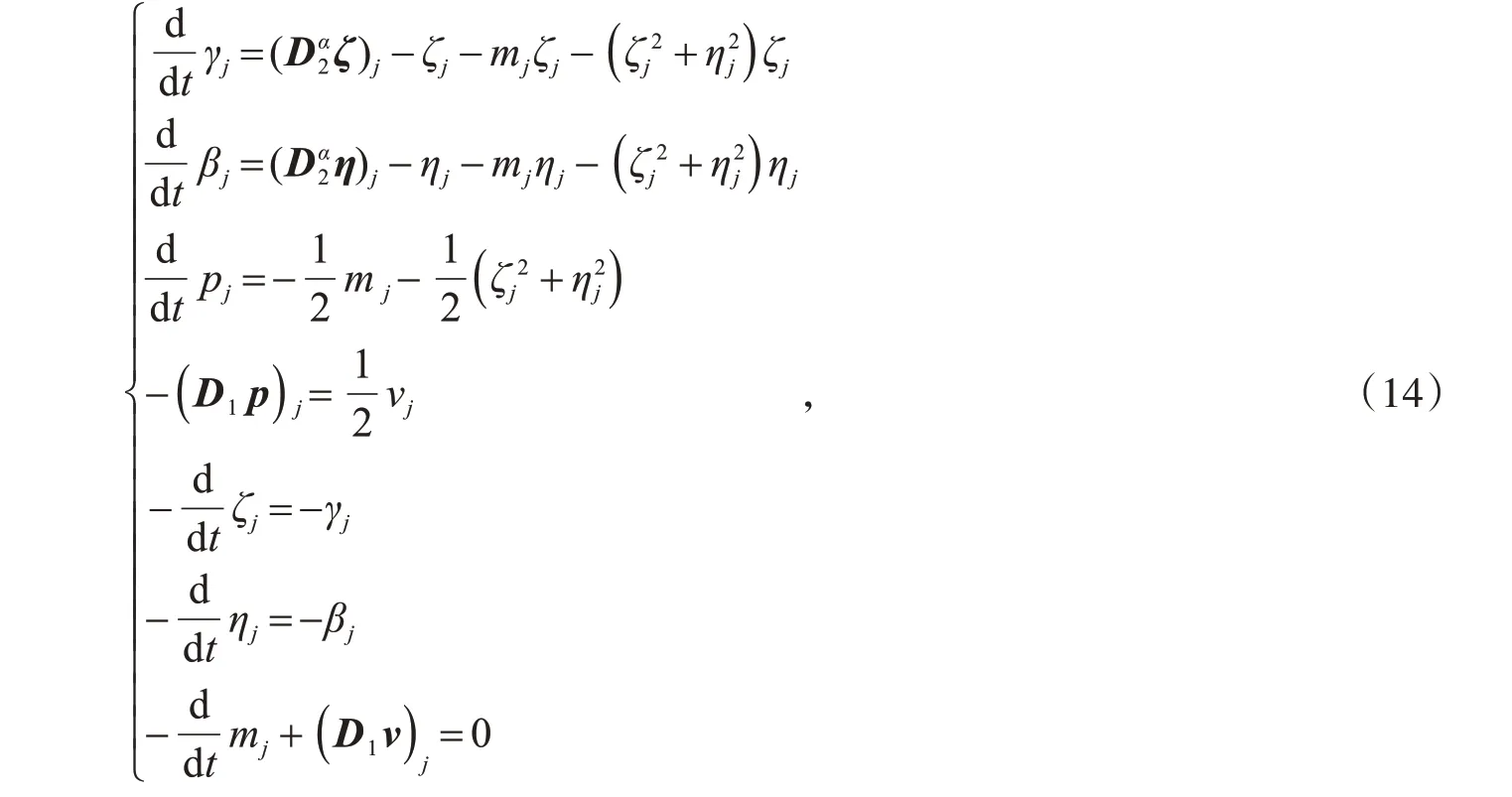
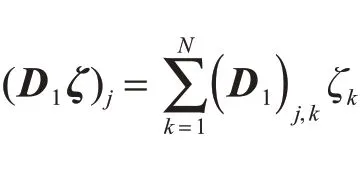
在时间方向上，对空间离散后的多辛系统（15）用二阶平均向量场方法［12］进行近似离散，有

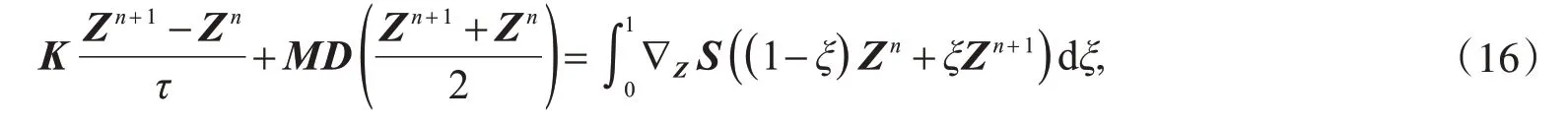
方程组（16）中消去变量γ，β，ζ，η.可得到如下离散格式

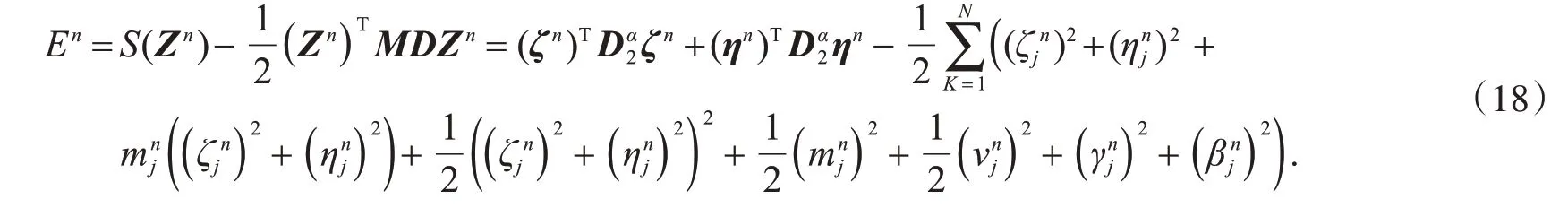
定理1 离散能量函数（18）关于时间是守恒的.

证明由于等式（15）可以写成

用二阶平均向量场方法对等式（19）进行离散，可以得到

其中，τ为时间步长，等式（20）可以写成

由于K是一个斜对称矩阵，则有下面等式成立

所以离散能量函数（18）保持能量守恒.

把格式（17）中向量u n+1，m n+1，v n+1，w n+1，p n+1，u n，m n，v n，w n，p n分别取为u n，m n，v n，w n，p n，u n-1，m n-1，v n-1，w n-1，p n-1，得到一组新方程组，再与原方程组相加减消去辅助变量w，v，p.从而得到一个新的方程组.

3 数值模拟

考虑分数阶KGZ方程在x∈[-10，10]和时间t∈[0，24]的数值解.新格式（22）是三层格式，取初始两步的初始条件为［9］

图1是方程在α=2和t∈[0，24]内|u(x，t)|和m(x，t)的数值解.从图1可知，数值结果与参考文献［9］一致，新格式能够较好地模拟方程数值解的行为.

图1 分数阶KGZ方程|u(x，t)|和m(x，t)在t∈[0，24]的数值解

图2是方程在α取不同值时的能量图.从图2可知方程在α取不同值时，随着时间的改变，能量一直保持不变，新格式保持方程的离散能量守恒特性.

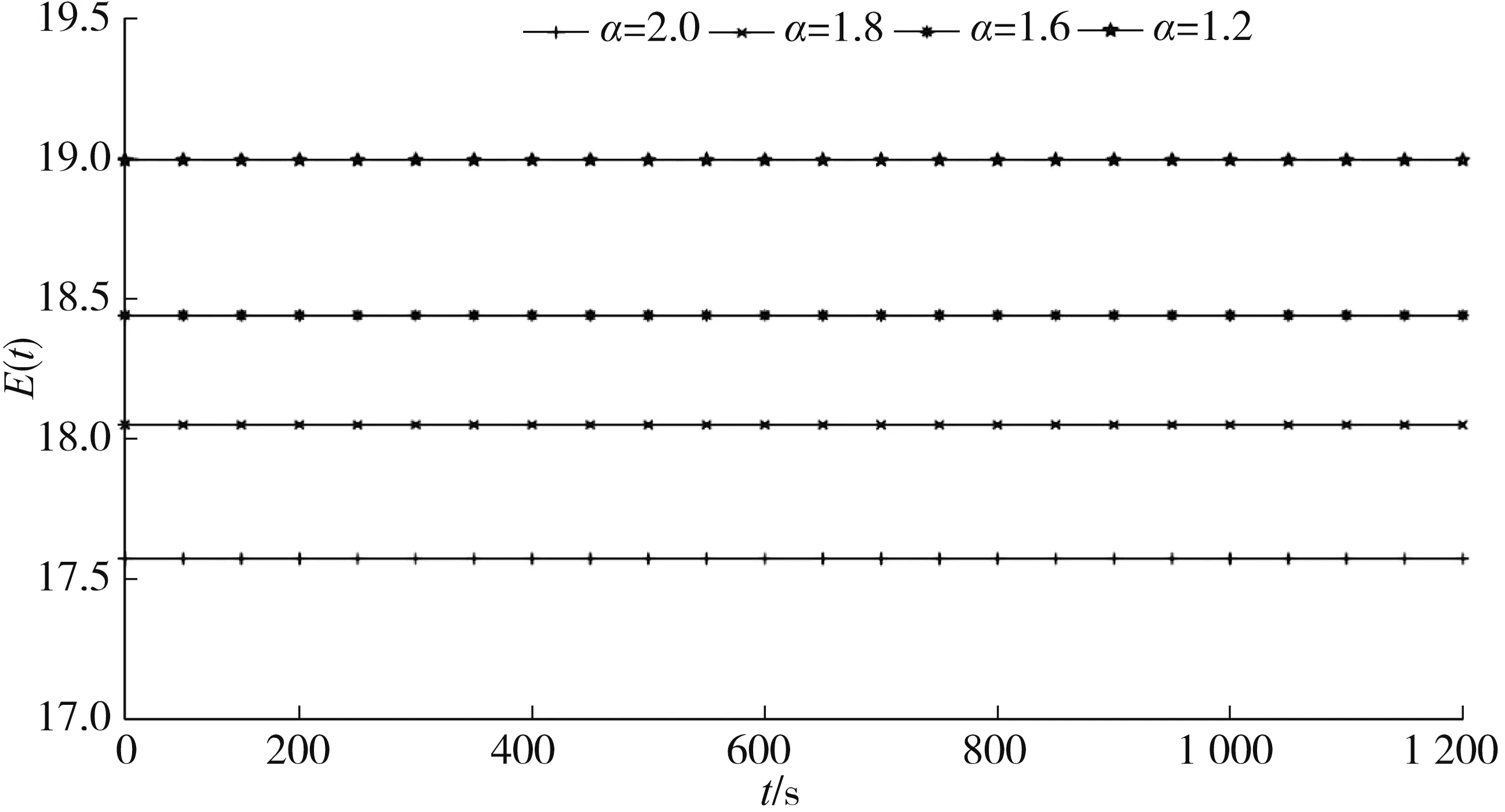
图2 分数阶KGZ方程在α取不同值时在t∈[0，24]的能量值与初始能量值的比较图.

4 小结

将分数阶Klein-Gordon-Zakharov方程写成多辛结构，利用傅里叶拟谱方法对Riesz空间分数阶导数离散近似，再利用平均向量场方法构造出Riesz空间分数阶KGZ方程新的保能量格式，用新格式数值模拟Riesz空间分数阶KGZ方程孤立波的演化行为.数值结果表明新格式能很好地模拟分数阶KGZ方程孤立波的演化行为并很好地保持了方程的离散能量守恒特性.显然，利用平均向量场方法在数值求解具有辛和多辛结构的分数阶偏微分方程中具有一定的优越性.