关于卡方复形的强shellable性质

郑 露，郭 锦

（海南大学理学院，海南 海口 570228）

单纯复形，简称为复形，是一种应用广泛的数学结构.在Stanley-Reisner对应之下，可以通过探讨单纯复形的顶点可分解、shellable等性质，研究其对应的单项式理想的（序列）Cohen-Macaulay等性质［1-4］.文献［5］给出了一类由复形Δ的一个染色χ出发构造的复形Δχ（卡方复形），并证明了这些复形Δχ都是纯复形且顶点可分解，因而是shellable纯复形，进而都是Cohen-Macaulay复形.

Guo等［6-7］定义并研究了一类特殊的shellable复形，称为强shellable复形.其优于一般shellable复形之处在于强shellable纯复形的极大面理想都具有线性商.

单纯复形与图论有着非常紧密的联系.对于一个有限简单图，可以定义其独立复形，该复形以图的顶点集作为基础集，以图的独立点集作为面.若图的独立复形具有某些特定性质，就称该图具有对应的性质.关于图的某类性质的研究也是组合交换代数的一个重要课题［8-11］.文献［12］中构造了各种“whiskered”图类，具有较好的组合代数性质，如顶点可分解、shellable、强shellable等.为探讨卡方复形的强shellable性质，笔者定义一类TA复形后验证了其上任一染色所对应的卡方复形Δχ都具有强shellable性质，并证明了复形Δ在任意一个染色χ下的卡方复形Δχ都是matroid，当且仅当Δ是单形.此外，还分析了“whiskered”图在复形层面上所对应的卡方复形是否具有类似的性质.

1 预备知识与卡方复形

对于顶点集V={x1，x2，…，x n}，定义在V上的一个复形Δ是V的一个子集族，满足：对任意F∈Δ以及G⊆F，都有G∈Δ.复形Δ里的元素叫作面，所有面中按照集合包含关系的极大者称为极大面，所有极大面构成的集合记作F(Δ).面F的维数定义为dim(F)=|F|-1，而复形Δ的维数定义为dim(Δ)=max{dim(F)|F∈Δ}.若Δ所有的极大面都具有相同的维数，则称Δ为纯复形.若Δ只有一个极大面，则称Δ为单形.

定义1 设Δ为一个复形，如果存在Δ的极大面集F(Δ)上一个全序F1，F2，…，F n，满足以下条件，则称复形Δ具有强shellable性质，而称该全序F1，F2，…，F n为一个强shelling序：

对任意的1≤i＜j≤n，存在1≤k＜j，使得以下3个条件同时成立：

1）|F jF k|=1；

2）F jF k⊆F jF i；

3）F kF j⊆F i.

定义2 设Δ为一个复形.若极大面集F(Δ)满足以下调换条件，则称Δ为一个matroid复形：对任意的A，B∈F(Δ)，以及任意的a∈AB，都存在b∈BA，使得(A{a})∪{b}∈F(Δ)成立.

设G为一个简单图，V(G)为其顶点集，E(G)为其边集.对于A⊆V(G)，若不存在x，y∈A，使得{x，y}∈E(G)成立，则A叫作图G的一个独立点集.图G所有独立点集组成的集合记为Ind(G).显然，对任意独立点集A，若B⊆A，则B仍然是一个独立点集.故Ind(G)也是一个复形，称为图G的独立复形，其极大面为图G的极大独立点集.若独立复形Ind(G)具有强shellable性质，则称图G为强shellable图.

在文献［5］中引入了平衡复形的定义.本文的主要研究对象卡方复形就是一类平衡复形.

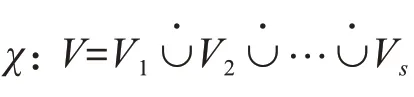
实际上，要求每一个面F i满足|F i∩F j|≤1，等价于要求每一个极大面F i满足|F i∩F j|≤1.

在文献［5］中给出了一类平衡复形的构造方法，对任意一个复形Δ及Δ上的任意一个染色χ，基于Δ的面可构造一些新的基数相等的集合，以这些集合作为极大面生成的复形，记为Δχ.为了表述的方便，称这类复形为卡方复形（χ-complex）.确切的定义如下.

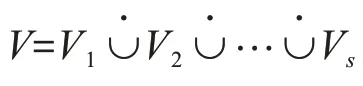
由构造1可知，卡方复形是纯的.易见，由一个s-染色所构造的卡方复形的维数为s-1.并且，该卡方复形是s-可染的，故为一个平衡复形，如例1所示.

例1 设Δ=x1x3，x2x3x4，χ：{x1，x4}∪{x2}∪{x3}为Δ的一个染色.那么集合Δ为如下集合：{∅，x3，x2，x2x3，x1，x1x3，x4，x4x3，x4x2，x4x2x3}.根据定义，Δχ的极大面集为F(Δχ)={y1y2y3，y1y2x3，y1x2y3，y1x2x3，x1y2y3，x1y2x3，x4y2y3，x4y2x3，x4x2y3，x4x2x3}.

定理1（文献［5］定理7）设Δ是一个复形，χ是Δ的一个s-染色，那么Δχ是顶点可分解的.

由定理1可知，对任意一个复形以及其上任意一个s-染色，Δχ总是顶点可分解的，而复形的顶点可分解性质与强shellable性质一般情况下不能互相推导［6］.因此，对卡方复形的强shellable性质的研究也有着非常重要的意义.

定理2（文献［5］推论9） 设Δ是一个复形，χ是Δ的一个s-染色，那么Δχ一个是shellable复形，且若F1，F2，…，F m是Δ所有面的一个升维排列序列，那么F1∪τ1，F2∪τ2，…，F m∪τm是Δχ的一个shelling序列.

由定理1可知，Δχ是一个shellable复形.定理2的后半部分则给出了Δχ的一个shelling序列的构造方法.受此启发，用类似的方法寻找Δχ的一个强shelling序列.

2 卡方复形的强shellable性与matroid性

主要研究卡方复形的强shellable性质.研究强shellable性质，需要构造强shelling序，因此定义了卡方复形极大面上的一个全序关系.

其中，

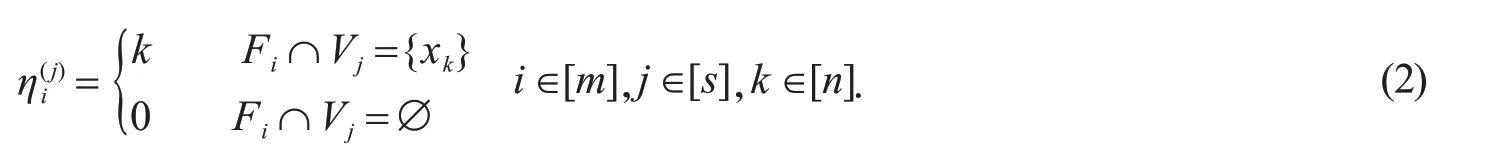
显然σ是一个单射.

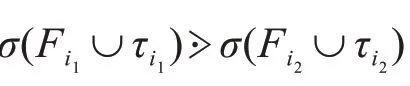
易见，≻χ为定义在Δχ所有极大面上的一个全序关系.例1中给出了一个卡方复形Δχ所有极大面的集合，其书写顺序就是按照≻χ的一个排序.

可以证明以下结论.

定理3 设Δ是定义在V={x1，x2，…，x n}上的一个复形.令染色χ：V={x1}∪{x2}∪…∪{x n}，那么Δ在染色χ下的卡方复形Δχ是一个强shellable复形.

证明设Δ={F1，F2，…，F m}，那么由构造1可知Δχ是V∪{y1，y2，…，y n}上的一个复形.下面证明该卡方复形极大面上的字典序是Δχ的一个强shelling序列.

对任意的1≤i＜j≤m，不妨设σ(F i∪τi)=(i1，i2，…，i n)，σ(F j∪τj)=(j1，j2，…，j n)，其中i r，j r∈{0，r}，r∈[n].由于F i∪τi≻χF j∪τj，那么由定义4可知存在r∈[n]，使得i1=j1，…，i r-1=j r-1，i r＜j r，所以有x r∈F jF i和y r∈τiτj.令F k=F j{x r}，易见F k∈Δ，则在F(Δχ)中有一个极大面为F k∪τk.直接验证可知，τk=τj∪{y r}.易见，F k∪τk≻χF j∪τj，且有

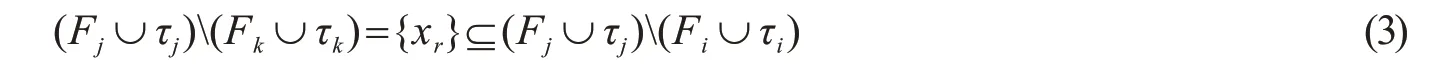
以及

由此可见，Δχ的极大面上的字典序是一个强shelling序列.因此，Δχ是一个强shellable复形.

在文献［9］中构造了一系列的“whiskered”图，从图的角度得到了以下结论，而通过定理3可以得到如下的一个结论.

推论1（文献［9］推论5.3）设G为一个简单图，其中顶点集V(G)={x1，x2，…，x n}，边集为E(G).在图G的基础上构造一个新的图G W，使得其顶点集为V(G)∪{y1，y2，…，y n}，边集为E(G)∪{{x1，y1}，{x2，y2}，…，{x n，y n}}.那么G W是一个强shellable图.

证明设Δ=Ind(G)，令χ：V={x1}∪{x2}∪…∪{x n}为Δ的一个染色.显然Ind(G W)=Δχ，那么由定理3可知Ind(G W)是一个强shellable复形，因此G W是一个强shellable图.

对于任意一个简单图，总会存在唯一一个独立复形与之对应，但并不是所有复形都能作为某个图的独立复形.故在复形上考虑的问题更具有一般性.

定理3说明对任意一个复形Δ，总会存在一个染色χ（即基础集上每个点染不同色），使得对应的卡方复形是一个强shellable复形.类似地，对于一个复形Δ，若Δ在任意一种染色下的卡方复形都为强shellable复形，则Δ应当满足某种条件.为了探究此条件，先引入以下概念.

设Δ为定义在基础集V上的一个复形，φ是V上的一个置换.定义映射

定义5 设Δ为定义在基础集V上的一个复形.若对任意不共面的2点x，y∈V（即{x，y}∉Δ），由x，y的对换φ，

所诱导的映射φˉ都是Δ的自同构，则称Δ为一个TA复形.

定理4 设Δ为一个TA复形，那么对于Δ的任意一个染色χ，Δχ是一个强shellable复形.

对任意的1≤i＜j≤m，不妨设σ(F i∪τi)=(i1，i2，…，i s)，σ(F j∪τj)=(j1，j2，…，j s)，其中i1，i2，…，i s∈{0，1，…，n}，j1，j2，…，j s∈{0，1，…，n}.由于F i∪τi≻χF j∪τj，那么由定义4可知存在r∈[s]，使得i1=j1，…，i r-1=j r-1，i r＜j r.

若i r=0，则F i∩V r=∅，所以y r∈τiτj，且存在x j r∈V r，使得x j r∈F jF i.令F k=F j{x j r}，易见F k∈Δ，则在F(Δχ)中有一个极大面为F k∪τk.直接验证可知τk=τj∪{y r}.易见，F k∪τk≻χF j∪τj，且

和

则在F(Δχ)中有一个极大面为F k∪τk.直接验证可知τk=τj.由于

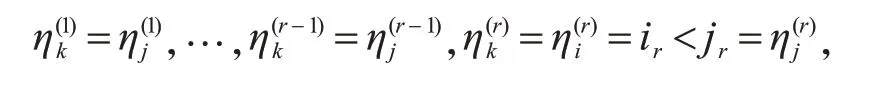
因此，F k∪τk≻χF j∪τj，且

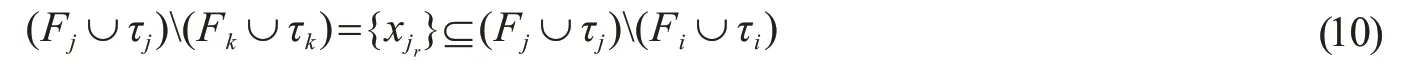
和

由此可见，Δχ的极大面集上的字典序是Δχ的一个强shelling序列.因此，Δχ是一个强shellable复形.

则对该复形Δ的任意一个s-染色χ，Δχ是一个强shellable复形.

证明易见这里所构造的复形Δ是一个TA复形，所以由定理4可知结论成立.

此外，直接检验可知，推论4中所构造的复形Δ是一个matroid复形，但在某些染色下对应的卡方复形Δχ并不是matroid复形.因此，考虑了一个复形应当具备怎样的性质，才能使得该复形在任意染色下对应的卡方复形总是matroid复形，且得出了如下结论.

命题1 设Δ是一个复形.那么，对于Δ的任意一个染色χ，Δχ是matroid的当且仅当Δ是一个单形.

证明设V={x1，x2，…，x n}为Δ的基础集.若Δ为一个单形，那么Δ= {x1，x2，…，x n}.显然，Δ只有一个染色，即V={x1}∪{x2}∪…∪{x n}，记为χ.令Δ={F1，F2，…，F m}，证明Δχ的极大面集上的字典序是Δχ的一个强shelling序列.

对任意的i，j∈[m]，i≠j，有a∈(F i∪τi)(F j∪τj)，此时有2种情形.

情形1a∈F iF j，不妨设a=x t，那么y t∈τjτi.取F k=F i{x t}，显然F k∈Δ，那么Δχ有一个极大面为F k∪τk，且τk=τi∪{y t}.进而有y t∈(F j∪τj)(F i∪τi)和

情形2a∈τiτj，不妨设a=y s，那么x s∈F jF i，进而有x s∈(F j∪τj)(F i∪τi).此时考虑F k=F i∪{x s}⊆V，由于Δ是一个单形，所以F k∈Δ.由此可知Δχ有一个极大面为F k∪τk，且τk=τi{y s}.于是

综上所述，Δχ是一个matroid复形.

反之，若对于Δ的任意一个染色χ，Δχ是matroid的.用反证法.假设Δ不是单形，那么Δ至少会存在2个不同的极大面F1，F2.令染色χ为V={x1}∪{x2}∪…∪{x n}.那么Δχ会存在2个不同的极大面F1∪τ1，F2∪τ2，其中τi={y j|{x j}∩F i=∅}，i=1，2.由于F1⊄F2，故F1F2≠∅，不妨设x1∈F1F2，那么y1∈τ2τ1.考虑F2∪(τ2{y1})，对任意的r∈[n]，r≠1，总有x r∈F2或者y r∈τ2{y1}.又因为Δχ是matroid的，故必有

由Δχ的定义可知F2∪{x1}∈Δ，这与F2是极大面矛盾，故Δ是一个单形.