随机子空间方法在去极化电流解谱中的应用
2022-01-25王亚兰
周 凯,王亚兰
(四川大学 电气工程学院,四川 成都 610065)
0 引 言
由于城市发展的需要,交联聚乙烯(Cross⁃Linked Polyethylene,XLPE)电力电缆被广泛用于城市配电网中。通常情况下,电力电缆的敷设环境极其恶劣,在长期服役的过程中,水分、电场和温度等因素会导致电缆中XLPE材料老化,引发电缆故障,造成非计划性停电。因此快速准确地评估电力电缆的绝缘状态对于保证电力系统的稳定运行具有重大意义。
极化去极化电流(Polarization and Depolarization Current,PDC)法是一种基于电介质介电响应理论的无损检测方法,该方法通过测量绝缘介质内部各种类型的松弛极化来判断绝缘介质的老化程度,具有接线电路简单,测试电压低,设备体积小等优点。目前,国内外学者针对PDC法对XLPE电缆的绝缘诊断开展了大量研究,文献[3]提出去极化电流曲线可以反映电缆的绝缘老化状态,但是没有深度探究表征电缆老化程度的特征量;文献[4⁃5]对去极化电流建立等效数学模型然后进行解谱分析,得到了各谱线参数对电缆绝缘老化的变化规律,但是该方法中去极化电流的子谱线数目都是事先设定,因此求解结果可能无法反映真实物理过程;文献[6⁃7]借助去极化电流的微分曲线峰值确定子谱线数目,然后计算各子谱线参数,该方法进一步完善了去极化电流解谱方法,但是存在微分曲线峰值的清晰度较差,子谱线数目计算结果受人为因素影响较大的问题;文献[8]提出利用去极化电流Hankle矩阵的奇异值大小进行分类进而判断子谱线数目,解决了微分曲线方法存在的问题,使得去极化电流解谱结果更加准确,但是进一步研究发现由于各信号奇异值的数量级差距太大,因此在实际运用中也存在一定的局限性。
因此,为了解决传统去极化电流解谱方法中存在的子谱线总数和子谱线参数难以求解的问题,本文提出一种基于振型幅值法结合随机子空间识别(Stochastic Subspace Identification,SSI)的去极化电流解谱方法。本文首先利用振型幅值确定子谱线数目,然后借助基于协方差驱动的SSI算法实现去极化电流各子谱线参数的求解。针对仿真去极化电流数据和实测去极化电流数据进行分析,同时和微分曲线峰值和奇异值定阶法进行对比,以验证该方法的有效性。
1 去极化电流等效数学模型
扩展Debye等效电路常用作电力电缆的等效模型,其具体模型结构如图1所示。

图1 电力电缆等效电路模型
图1中:R 为绝缘电阻,C 为几何电容,R 为极化电阻,C 为极化电容,为极化支路总数。从图1中可以看出,扩展Debye等效电路由绝缘电阻支路、几何电容支路和极化等效支路并联组成,由此确定去极化电流的表达式为:
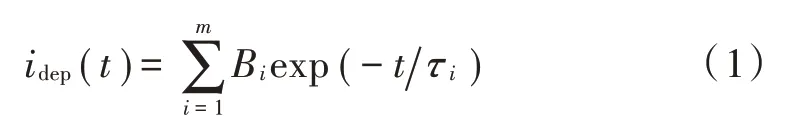
式中:B 为极化幅值系数;τ=R C ,为极化时间常数。
式(1)描述的电介质极化过程中去极化电流和时间的关系称为电介质的极化衰减函数,其中也表示去极化电流曲线中子谱线数,运用该等效电路模型评估电缆绝缘状态时,其关键在于准确提取式(1)中各参数。目前国内外学者通过设定值借助智能算法进行子谱线参数的提取,但是该方法具有较强的主观性,致使求解结果无法反映电力电缆中真实的弛豫过程。本文提出基于振型幅值法结合随机子空间识别的去极化电流解谱方法,来提取去极化电流中的子谱线参数,减少人为因素的影响,提高利用去极化电流的数学模型诊断电力电缆绝缘状态的可靠性。
2 去极化电流解谱算法
2.1 SSI
SSI作为一种系统模态参数估计的方法,具有识别精度高和数值简单的优点。按照矩阵投影方式的不同,SSI被分为基于数据驱动的SSI和基于协方差驱动的SSI。在保证数据信息量一致的情况下,基于数据驱动的SSI利用QR分解提取数据信息,而基于数据驱动的SSI利用托普利茨矩阵提取数据信息,由于QR分解的运算速度较差,导致基于数据驱动的SSI的运算效率更低,因此本文采用协方差驱动的SSI进行系统的模态参数估计,即本文采用协方差驱动的SSI对去极化电流进行解谱。
将去极化电流y 用一离散系统的状态方程表示为:
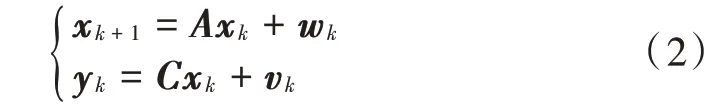
式中:是系统的状态矩阵;是系统的输入矩阵;x 和y 是系统时刻的状态量和输出量;w 是过程噪声;v 是测量噪声。
根据y 构造“未来”和“过去”的时延矩阵:

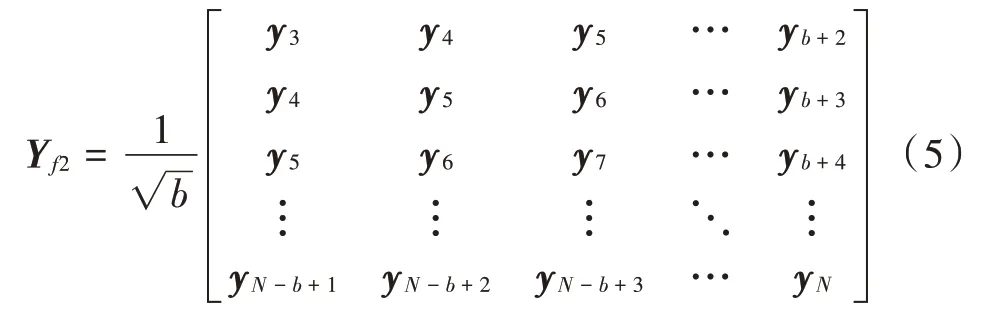
式中:表示y 的总数;表示时延矩阵的列数,为满足统计分析的需要和提高模态识别精度,的取值应尽可能大,但是实际的数据量有限,同时数据越多计算量越大。因此本文为了均衡计算的精度和成本,取>5(--1)。Y 表示“过去”时延矩阵,Y 和Y 分别代表第1和第2个“未来”时延矩阵。
进一步得到托普利茨矩阵为:

将进行奇异值分解,得到:
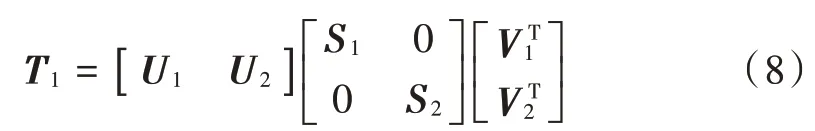
式中:T表示矩阵转置;,为奇异值对角阵;,及,分别是左、右奇异阵,1代表信号产生矩阵,2代表噪声产生矩阵。
因为w 和v 理论上互不相关,因此根据离散随机状态模型的性质可得:
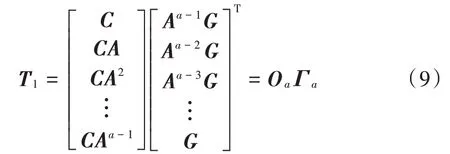
式中:O 是观测矩阵;=(x ),是期望;Γ是控制矩阵;=--1。
将式(8)和式(9)结合得到:
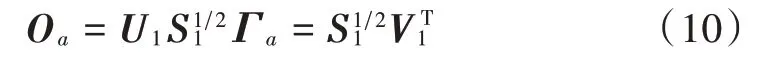
再根据式(9)可得:

结合式(10)和式(11)得到:
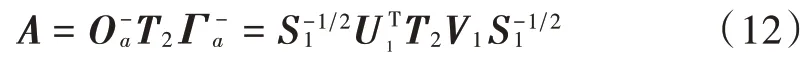
进一步对离散数据进行特征值分解:

式中:=diag(λ),=1,2,…,,λ为的特征值,为系统阶数;为特征矩阵。
得到对应λ的参数辨识结果为:

式中Δ为去极化电流的采样周期。
进一步通过式(15)得到B 。
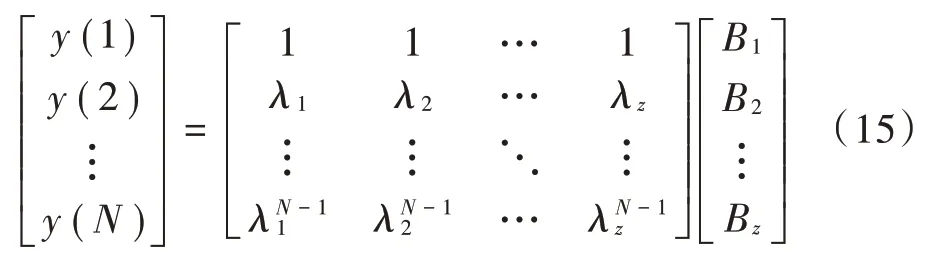
2.2 振型幅值法
对于SSI方法而言,在确定系统的阶数之后,便可以得到系统的模态参数,相对应去极化电流,当确定子谱线数后,SSI方法便可以有效识别各子谱线参数。文献[8]提出利用奇异值的大小定阶,但是进一步研究发现,由于各信号奇异值的数量级相差较大,因此实际运用中可能效果较差。本文利用SSI方法处理去极化电流信号,得到的振型对应去极化电流信号中B 的幅值,此时真实阶次的B 会呈现幅值较大的状态,虚假阶次的B 会呈现幅值较小的状态,借助B 的幅值可以确定真实阶次的数目。因此本文将SSI中定阶问题转化为B 幅值的截断阈值选定问题,即利用重新排序后的B 幅值确定去极化电流的子谱线数。
3 仿真测试分析
研究文献[12]中子谱线数为6条的去极化电流曲线,各子谱线数如表1所示,放电时间为180 s,采样周期为0.1 s,详细分析本文方法对去极化电流数据的解谱效果。假设系统的阶数是10,得到振型幅值图如图2所示。
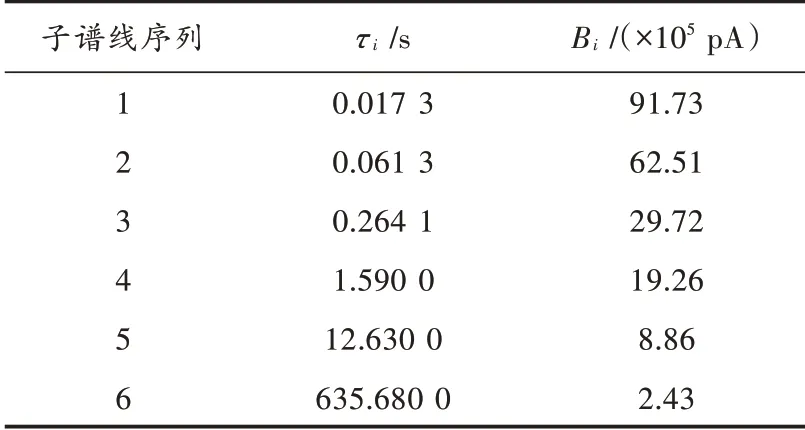
表1 仿真去极化电流的子谱线参数
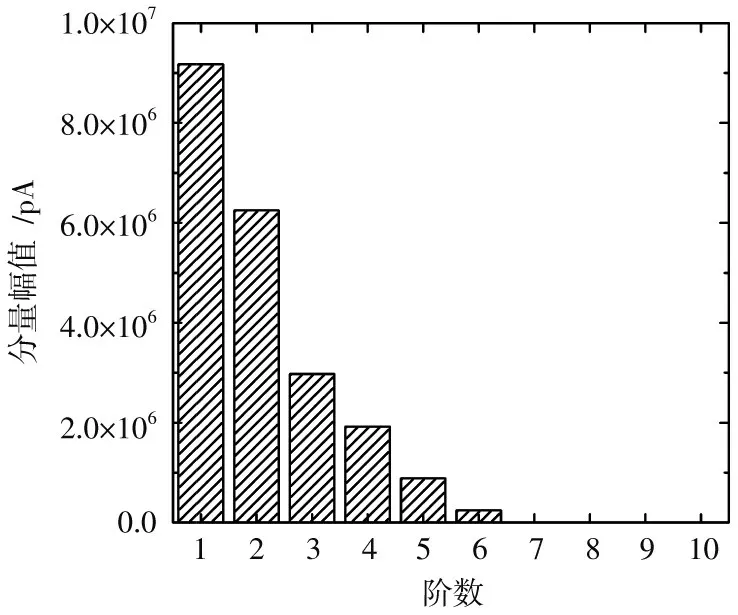
图2 仿真去极化电流的振型幅值图
从图2中可以看出,该系统中6类分量的幅值较大,因此确定系统的阶数为6,即确定该去极化电流存在6条子谱线,和仿真条件一致。在确定子谱线数后,利用SSI解析子谱线参数,得到其结果如表2所示,对比表1和表2可以看出,SSI算法可以准确求解去极化电流子谱线参数,为后续绝缘介质的状态评估提供合理依据。
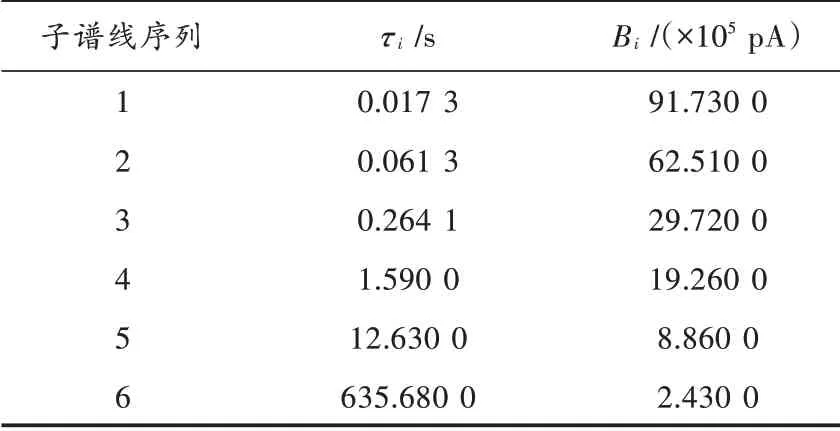
表2 仿真去极化电流的子谱线参数识别结果
为了进一步说明本文方法的优越性,构造奇异值变化曲线和微分谱线如图3所示。对于奇异值方法而言,由于各有效奇异值之间数值相差较大,因此难以准确确定去极化电流的子谱线数;对于微分谱线而言,一方面峰值难以确定,另一方面无法识别所有的子谱线,因此也难以准确得到去极化电流的子谱线数。
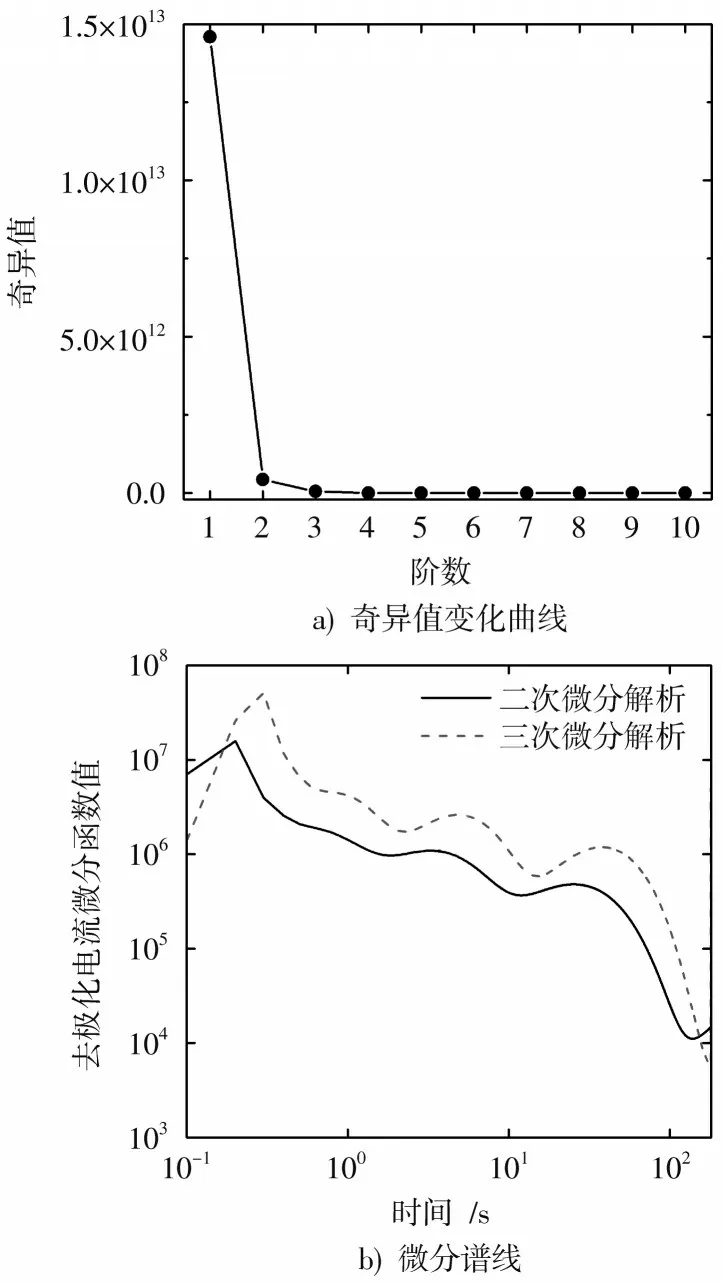
图3 仿真中传统方法的子谱线数识别结果
4 实际测试分析
4.1 实验设计
为了实际验证本文去极化电流解谱方法的准确性和可行性,本文对不同老化程度的水树老化电缆进行了实验分析。为了获得不同老化程度的水树电缆试品,本文用型号为YJV22⁃3×95,8.7/10 kV的500 mm短电缆试样作为实验材料,在实验室采用水针电极法进行电缆的水树加速老化。用钢针在样品外半导电层上等间距(3~5 mm)扎入1.5 mm深度的小孔,然后向热缩管的空腔中注入1.7 mol/L氯化钠溶液,并侵入铜电极接地,最后施加400 Hz,7.5 kV交流电压用于加速水树老化。试品在水针电极法下水树加速老化60天,并分别在0天、30天和60天对试品进行一次PDC测试。
在PDC测试中为了不损伤电缆绝缘和节省测试的时间,电缆绝缘的极化电压设置为1 kV,极化和去极化时间均设置为90 s。过程中采用Keithley 6485型皮安表记录PDC数据,实验回路如图4所示。图中K为继电器开关,在电缆两端的预留沿面上装上金属防泄漏环,并用导线接地以防止沿面泄漏电流的影响。每次测试前用无水乙醇将电缆两端的沿面绝缘进行擦拭并将缆芯和铜屏蔽层进行短接,以防止电缆中残留电荷对PDC测量产生影响。在测试时将试品置于屏蔽箱中并保证同一温度和湿度环境下测试,同时为消除开关抖动的影响,皮安表仅采集继电器动作1 s后的数据进行分析。
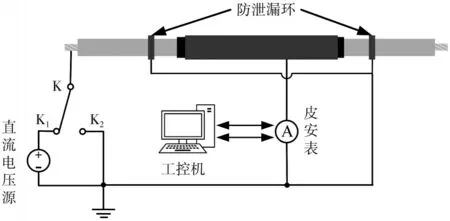
图4 PDC测量接线示意图
4.2 结果分析
测试得到不同程度水树老化电缆试品的去极化电流曲线如图5所示。
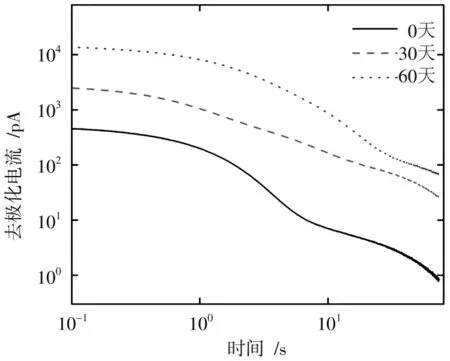
图5 实测的去极化电流曲线
从图5中可以看出,随着水树老化时间的增加,去极化电流幅值随之增加。这主要是因为:在水树老化的过程中,水分会在电场力作用下挤压XLPE材料,然后进入XLPE材料中的自由体内形成充水微孔,导致电缆绝缘中出现大量水和XLPE的界面,从而导致极化增强,宏观上表现为去极化电流幅值的增大。
利用本文方法对图5中去极化电流进行处理,假设系统的阶数是10,得到不同去极化电流的系统振型图如图6所示。
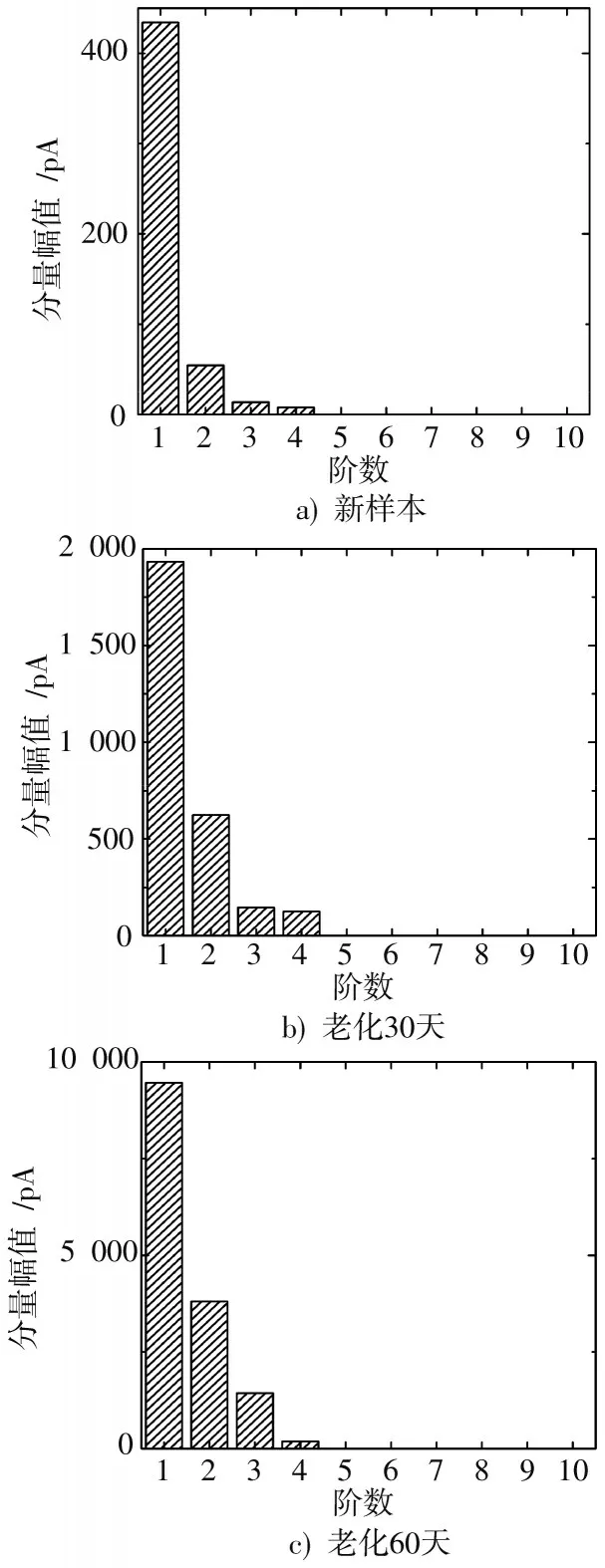
图6 实测去极化电流的振型幅值图
从图6中可以看出,3组去极化电流的系统阶数均为4,即确定3组去极化电流均存在4条子谱线,接着结合SSI算法流程,计算3组去极化电流的子谱线参数识别结果如表3~表5所示。
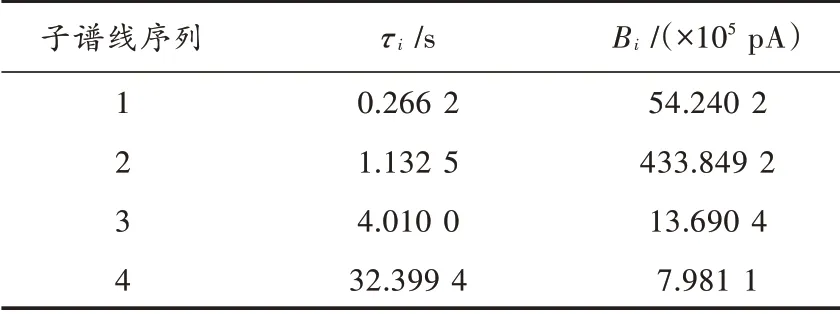
表3 新样本的去极化电流子谱线参数识别结果
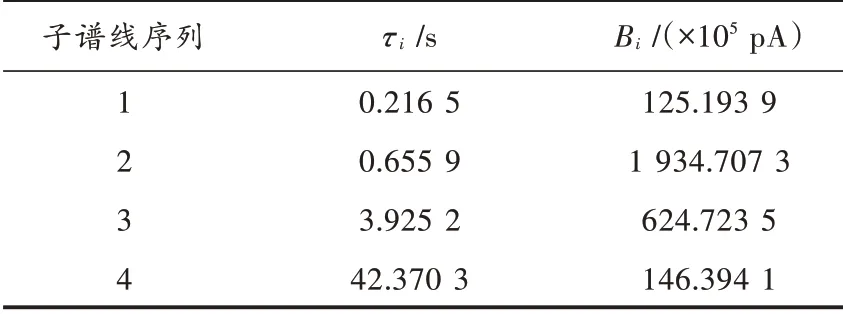
表4 老化30天样本的去极化电流子谱线参数识别结果
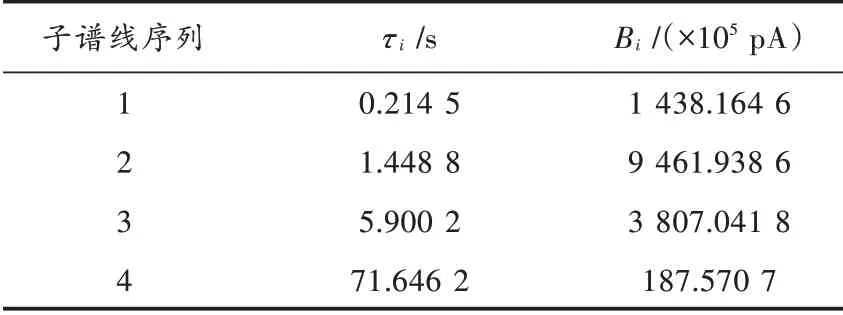
表5 老化60天样本的去极化电流子谱线参数识别结果
为验证识别结果的正确性,利用表3~表5中参数重构去极化电流曲线,得到仿真去极化电流曲线和实测电流曲线的对比结果如图7所示。
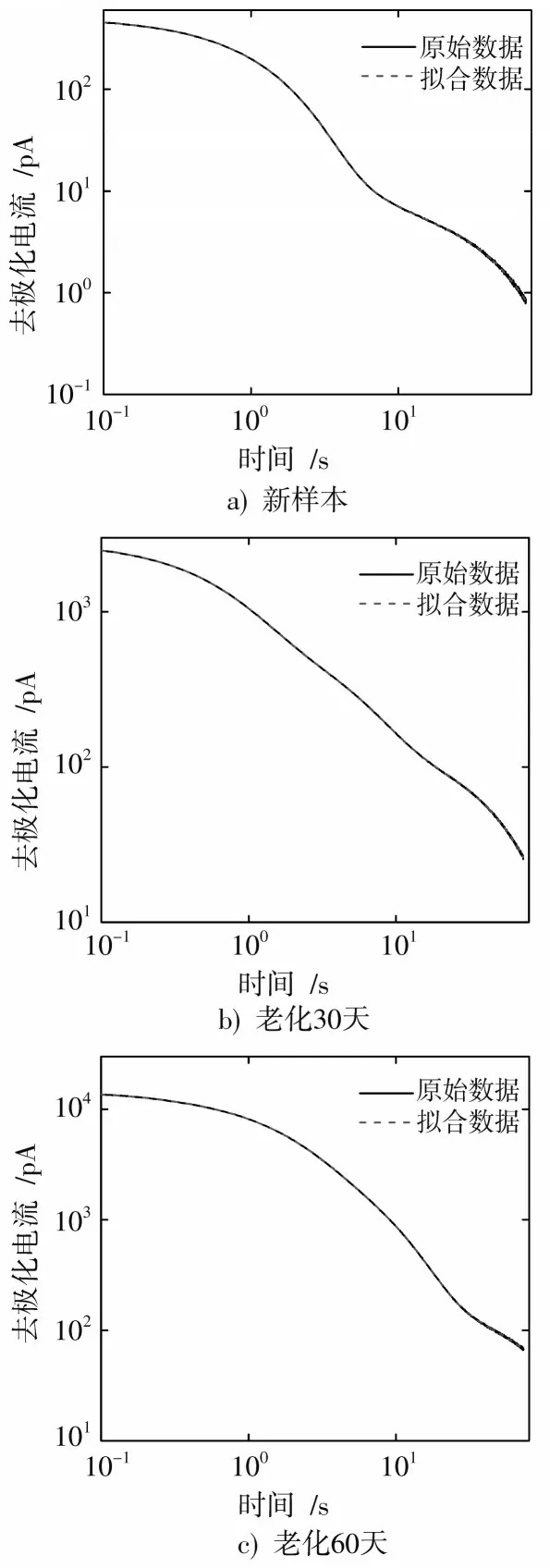
图7 原始数据和拟合数据的对比结果
从图7中可以看出,拟合数据和原始数据具有较高的吻合度,说明表3~表5中数据真实反映了电力电缆的极化特征,证实了基于振型幅值法结合SSI的去极化电流解谱方法的可靠性。
为了进一步证实本文所提方法的优越性,利用表3~表5中参数重构的去极化电流曲线构造奇异值变化曲线和微分谱线,如图8所示。
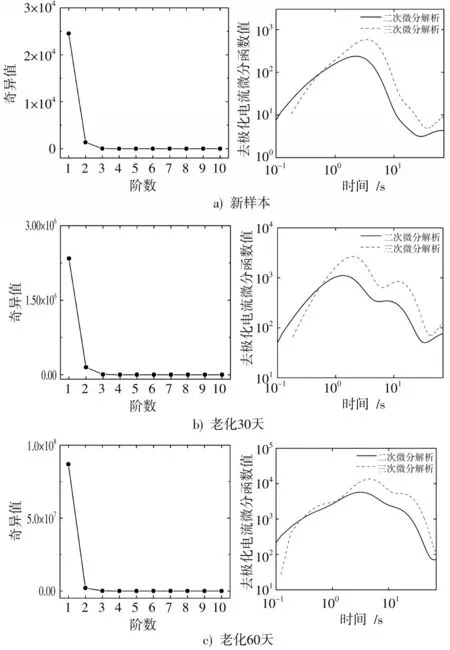
图8 实测中传统方法的子谱线数识别结果
从图8中可以看出,传统的奇异值方法和微分谱线方法均难以得到准确的子谱线数目,因此可能会造成去极化电流解谱出现错误,通过对比进一步验证文中所提方法的优越性。
5 结 语
针对传统去极化电流解谱方法中存在的子谱线总数和子谱线参数难以求解的问题,本文提出基于振型幅值法结合SSI的去极化电流解谱法。该方法首先通过去极化电流的振型幅值图确定子谱线总数,然后利用基于协方差驱动的SSI算法进行各子谱线参数求解,提高了去极化电流解谱的准确性,为评估电力电缆绝缘提供了新的思路。
