基于MEMS/GNSS 的多机协同无源定位

张 治，卢鸿谦*，班晓军，黄显林，刘雪梅

（1.哈尔滨工业大学 航天学院，黑龙江 哈尔滨 150000；2.航天飞行器生存技术与效能评估实验室，北京 100085）

1 引言

相比于有源定位，无源定位是指设备本身不主动发射电磁波，只接收、处理目标信号而完成定位的技术［1］。从未来战场环境的需求分析，无源定位具有良好的隐蔽特性和稳健的生存能力，且几乎不受干扰，环境适应性强、作用范围广［2］，因此成为现代电子战中不可或缺的重要环节，也是当前国内外研究的热点。按照观测量，用于无源定位的方法有多普勒频率变化率定位（Dop⁃pler Rate of Chang，DRC）、相位差变化率定位（Phase Difference Rate of Chang，PDRC）、测向交叉定位（Angle of Arrival，AOA）、到达时差定位（Time Difference of Arrival，TDOA）、频差定位（Frequency Difference of Arrival，FDOA）以及多种联合定位方法等［3-5］。

目前，对于无源定位的研究主要集中于军事需求，但无源定位也可在民用领域发挥巨大的作用。搭载无源定位功能的无人机可以更好地完成对非合作目标在复杂环境条件下的科研勘探、所搜定位、应急救援等任务。多无人机可简单且高效地利用视觉图像信息获取目标视线角，并以导航系统解算出的自身位置信息作为参考，基于AOA 定位算法完成对非合作目标的定位，本文基于此背景开展研究。

MEMS 惯组具有小型、轻便的特点，适用于作为无人船［6］、无人机等小型无人载具的核心导航设备。近年来，随着MEMS 惯组工艺的不断优化，该类传感器的性能参数不断提高［7］。使用较高精度的MEMS 惯组对于改善载机作为无源定位系统平台的自身信息准确性，从而改善定位性能有重要意义。MEMS 惯组无法单独定位，需要组合导航算法实现载具的定位，学者们基于不同的组合导航问题开展了研究。刘鹏飞引入里程计信息减轻了组合导航中出现的卫星信号失灵带来的导航发散［8］。邢东峰等提出了一种基于模糊方法和信息自适应估计的UKF 算法提升了低成本组合导航的速度和位置精度［9］。本文中载机所使用的SINS/GNSS 组合导航方法是一种被广泛应用的经典导航方法，简单可靠，满足对文中定位算法性能分析的需求。

在测角定位算法中，由于单站无法感知距离信息，基于测向的无源定位一般需要多站协同工作［10］。得益于所需量测量少、物理意义明确、原理简单和易于实现等特点，测向定位法一直以来都是无源定位领域的研究热点。在AOA 定位模型中，测量角与坐标状态变量之间的关系是非线性的。对于伪线性估计器的偏差问题，研究者将MLF 方法、最速下降法、高斯-牛顿法等应用于AOA 目标定位中［11-14］，用于补 偿或修 正这一 偏差。Pang 等在角度测量噪声先验信息缺失的情况下，通过将工具变量法与伪线性估计相结合所设计的估计器来提高系统估计的性能［15］。吴文龙、骆吉安等将最小二乘法、卡尔曼滤波等方法用于AOA 定位模型［16-17］。然而以上研究的条件设置中，测量站站址误差及测角误差均为高斯白噪声，所用方法旨在进一步提高系统在正常工作时的定位精度及计算效率。本文在众多研究成果的基础上，利用实测的某型号高精度MEMS惯组的噪声数据，对使用SINS/GNSS 组合导航算法计算载机导航参数时的性能表现进行了研究，使结果更加贴近实际应用。然后，使用载机位置解算结果作为基站坐标，将扩展卡尔曼滤波应用到测角定位算法中，给出对目标的定位信息估计。最后，将具有较强容错能力的联邦卡尔曼滤波应用于多机协同定位算法中，结合实际系统中可能出现的情况设计了一种含有故障的子系统，并在该情况下利用联邦滤波算法提高了系统的容错能力和可靠性。

2 工作原理

2.1 基于AOA 算法的双机协同定位原理

本文基于实际应用需求，载机自身的导航定位参数通过基于MEMS 的捷联惯导系统与GNSS 的组合导航获取。在多机协同定位非合作目标的过程中，每架载机以自身为主机即载机A，其他载机为辅机即载机B，在主机体坐标系下建立状态方程。在本实验的仿真条件中，基于扩展卡尔曼滤波对目标M 进行定位。基于AOA 定位算法的原理如图1 所示。其中，A，B，M代表不同载机的几何中心。

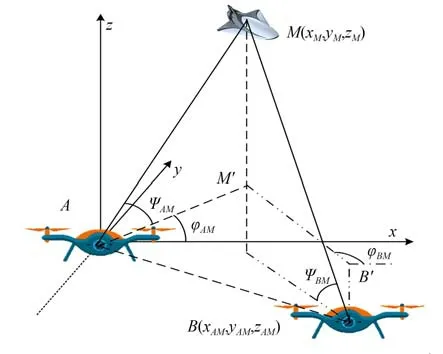
图1 双机测角无源定位模型Fig.1 Passive positioning model of double-machine an⁃gle measurement

图1 中，载机通过组合导航系统测得载机A的位置坐标为（xA，yA，zA)，载机B 的位置坐标为(xB，yB，zB)，M 为待定位目标。则在A的体坐标系下，B 的坐标为（xAB，yAB，zAB)。B'，M'分别为B和M在A的体坐标系中xoy平面的投影点，(φAM，ψAM)，(φBM，ψBM)分别为A，B对M的视线角。利用载机及目标的空间坐标与载机对目标视线角之间的几何关系，建立基于载机体坐标系的状态方程，并对目标M进行定位。

2.2 多机协同定位原理

基于AOA 测角定位模型，以仅有视线角的双机无源定位算法为基础，可拓展到多机对非合作目标的定位。以3 架载机A，B，C 对非合作目标定位为例，由卡尔曼滤波、数据融合等模块实现对非合作目标的定位。3 架载机中每两架为一组，可组合成3 个独立的子系统。以载机A 为例，以A 为主机，可获得AB，AC 两个子系统，测量计算所得的两组目标定位信息，利用联邦卡尔曼滤波对两组数据进行融合，获得目标与A 的相对状态最优估计。而当某个子系统出现故障无法实现精确定位时，本文所采用的联邦卡尔曼滤波器也能够自适应地对错误数据进行隔离，保证全局定位数据的最优性和可靠性。B，C 可使用相同的算法实现对目标的定位。

3 基于MEMS 组合导航的多机协同定位算法

3.1 载机的SINS/GNSS 组合导航定位算法

选取东-北-天为导航坐标系，若Φk为k时刻据陀螺仪输出计算所得的旋转矢量，则由旋转矢量计算所得的四元数变化公式为：

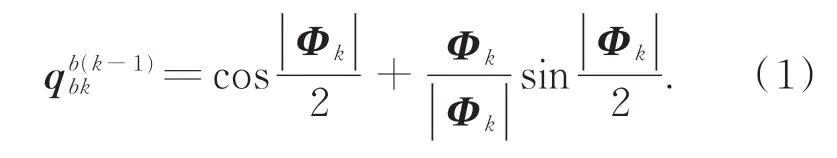
另有速度、位置更新公式如下：

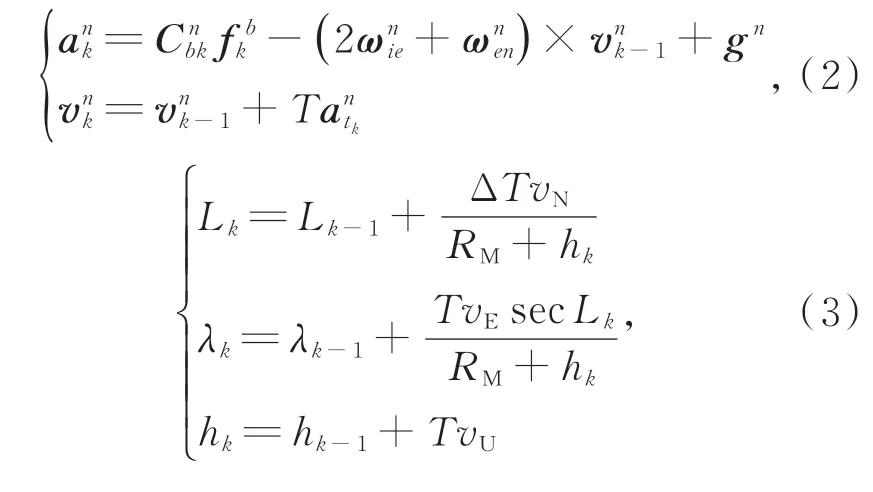
式中：L，λ，h，ΔT分别为纬度、经度、高度与时间间隔，RM以及后文中的RN为当地子午圈、卯酉圈半径。

使用SINS/GNSS 松组合模型，选取失准角、速度、位置误差、以及陀螺加表的随机常值偏移作为状态，即有：

系统状态方程可由捷联惯导的误差传播方程推导出，如下：

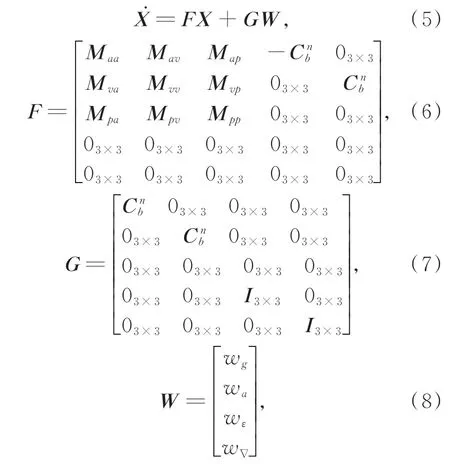
其中：下标a代表姿态、v代表速度、p代表位置，系统方程中的矩阵M为误差量间的关系矩阵；wε，w∇是为了避免随机常值对应的系统噪声阵过度收敛而加入的虚拟噪声。陀螺可敏感到地球自转角速度，故无需简化该模型。

选取速度、位置误差为量测量，量测方程为：

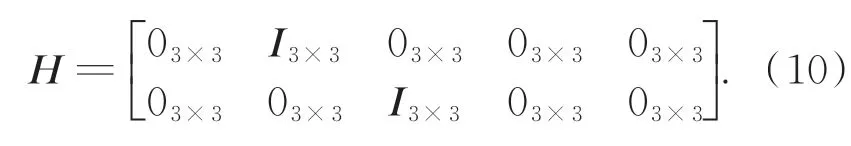
为了方便后续处理，经组合导航算法修正的载机坐标需统一由经-纬-高坐标系转化至地心地固坐标系，其转换公式为：

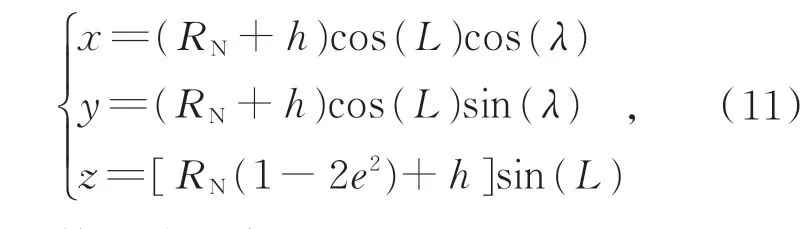
其中e为第一偏心率。

3.2 基于组合导航参数的测角定位几何精度误差分析

几何精度因子（Geometric Dilution of Preci⁃sion，GDOP）能够直观地描述目标与定位基站的相对位置与理论定位误差的关系。在获得组合导航定位误差参数后，本文利用GDOP 分析目标在双机和典型多机编队下的误差分布情况。

假设有N架载机对目标进行定位，目标的定位坐标与各载机的角度测量值的关系可表示为：

式中：(x，y，z)为目标的坐标，(xi，yi，zi)为第i架载机的坐标(i=1，2，…，N)，(φi，ψi)为第i架载机对目标的视线角测量值。求导可得：

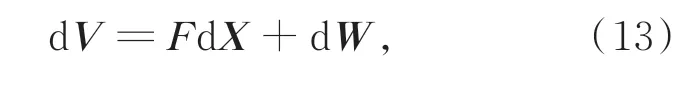
式中：

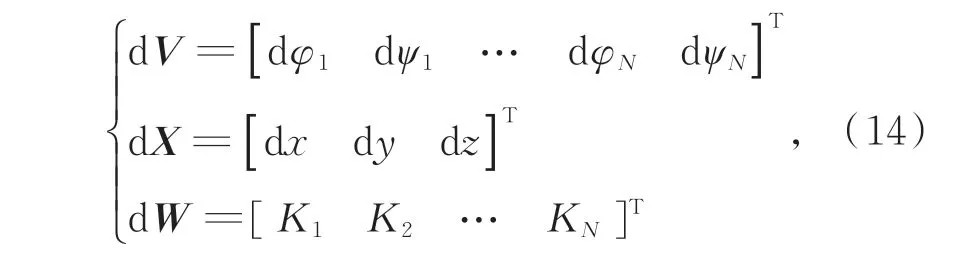
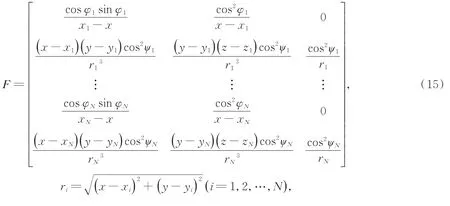
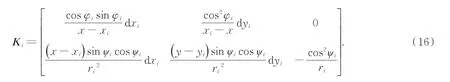
则误差的协方差阵为：

其中B=(FTF)−1FT。那么，测角定位法的GDOP 表达式为：

图2 为基于组合导航获得的载机定位误差下，几种典型布站方式的GDOP 等高线分布图。除载机导航误差参数之外，其他仿真条件为：载机间最短距离为1.5 km，测角误差为0.5°，载机高度为0，目标高度为5 km，载机布站中心点为坐标原点，观测目标在x=−15～15 km、y=−15～15 km 内移动时GDOP 理论值的分布。

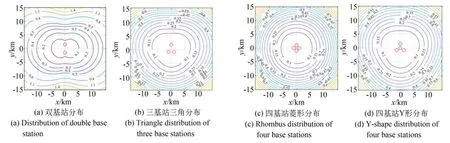
图2 典型基站分布下的GDOP 等高线分布图Fig.2 GDOP contour distribution under typical base station distribution

由图2 可知，在距中心5 km 时，理论定位误差为0.1 km，在实际应用中0.1 km 的定位误差是不能接受的，因此，需进一步研究基于AOA 的定位算法。

3.3 基于EKF 的双机协同定位算法

在系统最优估计的应用中，卡尔曼滤波的贡献是很大的，但目标的坐标与观测角的关系是非线性的，本文应用扩展卡尔曼滤波给出对目标定位的最优估计。通过组合导航获得的载机A 的状态为，载机B的状态为为获得目标M相对A 的坐标及速度，以A 为主机，B 为辅机，在A 的体坐标系下，定义状态变量X=为M 在A 的体坐标系下的坐标-速度分量。B 在A 的体坐标系下的状态为，A 的状态 为ψA）为载机A对目标的视线角，（φB，ψB）为载机B对目标的视线角。依据载机A，B 及目标M 的坐标与Z的关系，k时刻动态系统可描述为：

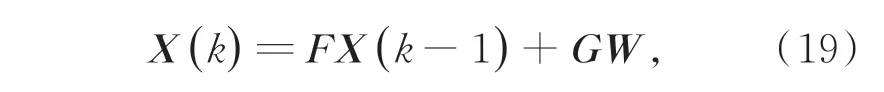
A，B 对M 的观测方程可描述为：

其中V为系统过程噪声和测量噪声。可见，观测方程为非线性方程，则扩展卡尔曼滤波流程可描述为：

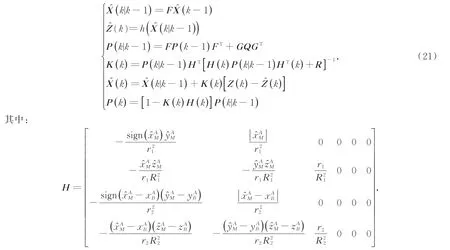
3.4 基于联邦滤波的多机协同定位算法

基于联邦滤波器的思想，在多机协同定位的情况下，为降低算法的维度，提高计算效率，并增强系统的容错能力，本文将每两架作为一个分系统，基于3.3 节的双机协同定位算法，完成多机协同定位。以A，B，C 三机为例，AB，AC 分别组成两个分系统，利用各子系统单步滤波更新之后的协方差阵的迹设计信息分配系数，具体联邦滤波算法流程如下：

（1）系统过程噪声为Q，用k−1 时刻的全局最优估计X(k−1)更新各子系统k−1 时刻的状态，各子系统的状态协方差阵为Pab(k−1)、Pac(k−1)，根据信息守恒原则，设计：

（2）对k时刻的状态进行估计：各子系统利用3.2 节的算法处理自己的量测信息，获得局部最优估计Xab(k)，Pab(k)，Xac(k)和Pac(k)；

（3）对分配系数γab，γac和子系统过程噪声协方差阵Qab，Qac进行更新；

（4）获得全局最优估计：

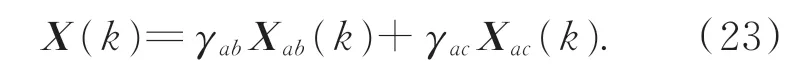
由式（22）可得，假设AC 子系统的某一状态估计值误差较大，则其对应的协方差阵的迹也较大，信息分配系数γac会减小，AC 子系统的信息在全局估计的影响也会减小。根据信息守恒原则，γab将大于γac，进而增加AB 子系统在全局估计中的影响。AC 子系统的估计结果误差越大，甚至接近无穷大，此方法对错误信息的隔离效果越好。

4 仿真结果

本文仿真中所用MEMS 及GNSS 参数见表1。本文仿真设置为A，B，C 三架载机协同对目标完成定位，系统仿真时间为140 s，前30 s 只做基于MEMS 的组合导航参数解算，之后组合导航参数解算基本稳定，与多机协同定位算法同步进行。载机对目标的视线角测量误差为0.5（˚3σ）的高斯白噪声，系统采样频率为1 kHz。理论上，如果一个系统是滤波稳定的，那么滤波初值是任意给定的，本文将利用载机的坐标及对目标的视线角信息，经过三角形解算获得的目标相对坐标作为滤波初值，以保证系统能够更快收敛。

表1 MEMS 及GNSS 的性能参数Tab.1 Performance parameters of MEMS and GNSS

4.1 系统在正常环境下的仿真

当AB 子系统、AC 子系统均能正常工作时，通过仿真可以得出以下结论：（1）从图3～图4 坐标误差、速度跟踪曲线和相对距离误差得出，无论是基于联邦滤波的多机协同定位算法，还是基于EKF 的双机协同定位算法，经过有限次迭代后，都能够给出高精度的定位结果；（2）值得注意的是，由于本文初值选取的方式，图4 的初始距离误差在百米量级，这与本文3.2 节GDOP 误差分布是吻合的；（3）经过数据分析，原本AOA 定位算法的理论误差在百米量级，本文的算法将相对距离误差降到了10 米量级，这样的误差水平在实际应用是可以接受的；（4）联邦滤波与子系统EKF 滤波在精度上并没有差别，在没有更高精度的测量值的情况下，增加载机数量并不能提高定位精度，但联邦滤波能够提高系统的可靠性和容错能力。也就是说，如果个别载机由于自身定位不准、无法识别目标等因素造成单个子系统不能对目标完成定位或定不准，整个系统也能够利用其他正常工作的子系统的信息完成对目标的定位，保证任务成功。

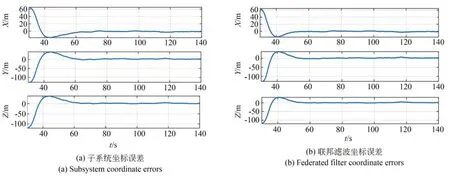
图4 联邦滤波与子系统EKF 滤波相对距离误差对比Fig.4 Comparison of relative distance errors between federated filter and subsystem EKF

4.2 子系统故障时的仿真结果

假设载机B 由于自身系统故障或受到干扰不能正确接收GNSS 信号，导致自身导航参数出错，且AB 间距离远小于目标与A，B 的距离，综合造成AB 子系统对目标定位不准，其他仿真条件不变，仿真结果如图5∼图7 所示。

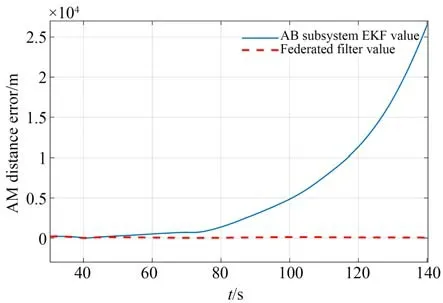
图5 联邦滤波与AB子系统EKF滤波相对距离误差对比Fig.5 Comparison of relative distance errors between federated filter and EKF of AB subsystem

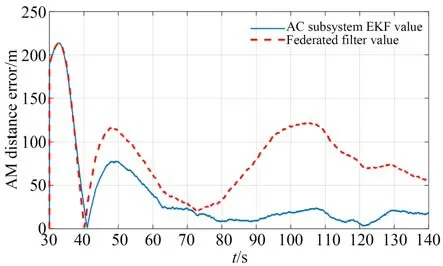
图6 联邦滤波与AC子系统EKF滤波相对距离误差对比Fig.6 Comparison of relative distance errors between federated filter and AC subsystem EKF

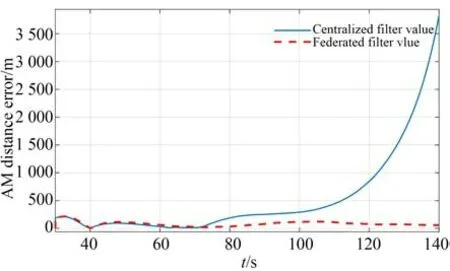
图7 联邦滤波与集中式滤波相对距离误差对比Fig.7 Comparison of relative distance errors between federated filter and centralized filter

图5 显示，AB 子系统的定位误差已经超过了2.0×104m，但联邦滤波的结果要远好于AB子系统的结果。由图6 可知，联邦滤波的结果虽不及AC 子系统的滤波结果，但联邦滤波的结果在100 s 之后，由于AB 子系统滤波结果的急剧增大，联邦滤波误差反而呈下降趋势。图7 给出了联邦滤波与集中式滤波的对比结果，集中式滤波由于综合了所有子系统信息，在AB 子系统误差急剧变化的情况下，集中式滤波的全局估计误差也急剧增大，联邦滤波则展示了隔离错误的能力。为更加清晰地对比不同定位算法的性能，表2 给出了各子系统及全局联邦滤波算法获得的20∼100 s 之间相对距离误差均值、误差率（相对距离误差/相对距离×100%）及相对速度标误差均值。

表2 不同定位算法相对距离及速度误差对比Tab.2 Comparison of relative distance and velocity errors of different positioning algorithms

5 结论

本文基于MEMS/GNSS 获取的载机导航定位参数展开对多机协同无源定位算法的研究。在一个解算周期内，首先基于民用MEMS 的实测误差数据，通过组合导航算法解算载机的定位参数；然后在仅有载机对目标的视线角测量的情况下，基于导航解算获得的载机坐标，利用EKF通过测角定位算法给出对目标相对载机的定位信息的最优估计。此外，为提高系统的可靠性，本文基于联邦卡尔曼滤波对目标完成多机协同定位。仿真实验表明，基于EKF 的测角无源定位算法在通过MEMS/GNSS 解算载机导航参数的情况下，将理论定位误差从100 m 量级降到10 m 量级，完成对目标的定位；相比集中滤波，基于联邦卡尔曼滤波的多机协同定位算法，能够在某载机导航定位出现故障，子系统对目标定位出现严重偏差的情况下，大大降低对全局定位信息的影响，提高了全局定位的精度。多机协同定位算法在基于MEMS/GNSS 组合导航算法获取载机坐标的情况下能完成对目标的定位，且利用联邦滤波算法能够对子系统载机因自身定位不准及轨迹偏差等因素造成的错误数据进行隔离，保证全局估计的有效性和可靠性。在当前研究中，量测信息为含有高斯白噪声的模拟数据，项目团队的进一步研究将在真实量测数据下展开。