生产周期和猪瘟影响下的猪肉商品微分动力系统分析

高德宝，邵云虹，徐 磊

近些年来，猪肉价格大起大落的戏码频频上演，已是见怪不怪.但“价高伤民，价贱伤农”，百姓深受其苦.牛肉与羊肉等肉类商品也会偶尔地表演一番价格飙升与骤降.猪肉商品价格飙升与骤降的根本原因是供需不平衡.而导致其供需不平衡的主要原因有两个：一是受生产周期影响，供应量与需求量发生博弈战，而供应量与需求量之间的博弈战是通过价格表现的.价格暴跌意味着供应量远大于需求量，价格飙升表明需求量远大于供应量.二是瘟疫对生猪的影响：它导致合格猪肉商品供应量急剧减少，同时瘟疫亦会导致其需求量的降低（例如2018年的非洲猪瘟导致我国猪肉需求量与其价格急剧下降）.而瘟疫结束后的一段时间内，价格又会急剧飙升.

供应量随着价格的变化而变化.当价格升高时，猪农会增加生猪的存栏量；当价格降低时，猪农会减少存栏量.而价格升高时，猪肉的需求量会减少；价格降低时，猪肉的需求量会增加.由此可见，供应量、需求量和价格之间的动态关系类似于捕食者与被捕食之间的关系，供应量捕食价格，价格捕食需求量［1-4］.而瘟疫对猪肉商品的冲击作用相当于生物数学中的脉冲扰动作用［5-7］.

我国猪肉价格频繁大起大落的原因，以及瘟疫对供应量、需求量和价格三者产生了何种影响，本文应用微分动力学的相关理论研究上述两个问题的内在驱动关系［8-11］.

1 生产周期影响下猪肉商品动力模型的构建与分析

猪肉等肉类商品的即时供应量是上一个生产周期内生产的，所以其供应量的实现具有时滞性.一般情况下，供应量和需求量均会随着价格的变化而变化，价格能够实时地反映肉类的供应量与其需求量之间的动态关系［12］.为建立数学模型，需作以下模型假设.

①对需求量、价格和供给量统一量纲，比如统一为货币单位.

②猪肉的平均生产周期为τ(τ＞0).

③猪农根据现时价格决定下一个周期内猪肉的供应量.

④假设t时刻，猪肉商品的需求量、价格和供应量分别为D(t)，P(t)，S(t-τ).

⑤因为需求量对价格的反应比较灵敏，所以假设需求量与价格之间的功能性反应具有线性关系.

⑥受消费人数的限制，假设需求量具有密度制约性并且需求量不完全依赖于供应和价格.

⑦假设猪肉价格仅受需求量与供应量的影响.因为需求量增加时，价格上涨，供给量增加时，价格下降，所以本文假设价格对需求量和供给量的功能性反映函数为

⑧因为t时刻猪肉的供应量S(t)是由tτ时刻的价格P(t-τ)决定的，所以假设供给量对价格的功能性反映函数为c1P(t-τ).

综上分析与假设，则仅受生产周期影响的猪肉商品微分动力系统为

其中：a0，a1，a2，b0，b1，c0，c1，w均为正数.基于问题的实际意义，系统（1）的可行域为

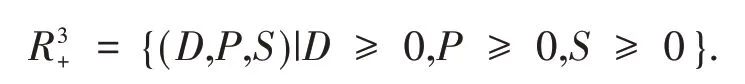
系统（1）在[-τ,0)内的初始条件满足

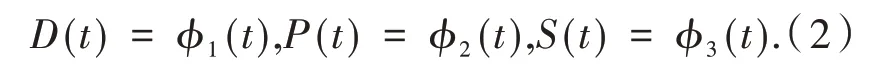
其 中：(ϕ1(t)，ϕ2(t)，ϕ3(t))∈C([-τ，0]，)，表示从区间[-τ，0]映射到的所有连续函数所构成的空间.

显然，系统（1）的右侧是光滑的，根据微分方程解的存在性与唯一性定理知：系统（1）满足初值条件（2）的解(D(t),P(t),S(t))在全局上是唯一存在的［13-14］.

定理1系统（1）以D(0)＞0,P(0)＞0，S(0)＞0为 初 值 的 解(D(t)，P(t)，S(t))具 有 非负性.

证明 易知系统（1）的前两个方程等价于以下两个方程：

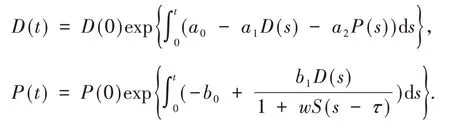
显 然，当D(0)＞0,P(0)＞0时，D(t)＞0,P(t)＞0.因为S′(t)|S=0=c1P(t-τ)＞0，所以S(t)＞0.

综 上 可 得，D(t)＞0，P(t)＞0，S(t)＞0，t∈[0,+∞).

基于社会的实际情况，不管价格如何，总会有人买一些猪肉来食用，也就是说需求量必定大于零.受猪肉生产成本的制约，其价格必定大于零.尽管偶尔会有猪瘟或其他影响猪肉质量因素发生，但是合格猪肉的供应量或多或少都是存在的.因此，定理1的结论与实践状况相符合.

定理2系统（1）在[0,+∞)内一致有界［8］.

证明 作函数V(t)=b1D(t)+a2P(t)，则有

易知P(t)在[0,+∞)上是有界连续函数，不妨设MP是它的一个上界.根据系统（1）的第3个方程可得

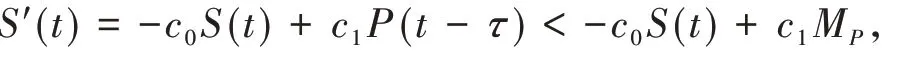
根据文献［11］的引理1.1.10可得

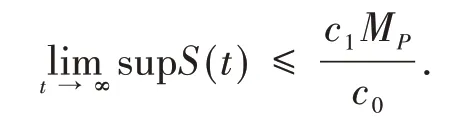
综上可得，定理2的结论成立.

定理2也可进一步地说明D(t)，P(t)，S(t)在[0,+∞)上有界.容易理解：因为消费者的人数是有限的，所以需求量必定是有限的.价格越高，猪肉的销售量会越少.当价格超出大多数人的消费能力范围时，购买猪肉的人们会更少，所以价格必须在绝大多数人的接受范围内.也就是说价格需要有上限.对于供应量而言，不是越多越好.当供应量远大于需求量时，其价格会很低，养殖户的利益会大大减小，因此猪肉的供应量必然有上限.这些实际状况与定理2的结论吻合.

通过求解方程组

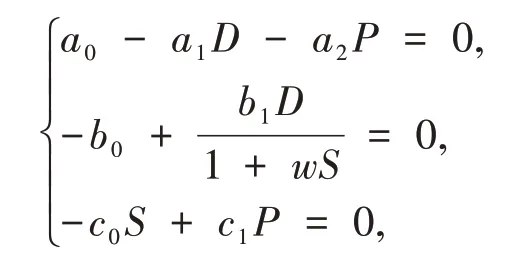
可得如下定理.

定理3若条件H1:a0b1-a1b0＞0成立，则系统（1）存在唯一的正平衡点(D*,P*,S*)，其中

在无其他因素影响的条件下，正平衡点(D*，P*，S*)是需求量、价格和供给量经过一段时间博弈之后所处的平衡状态.

2 局部稳定性和Hopf分支的存在性

定理4若系统（1）满足条件H1和条件

则存在τ0＞0，使得系统（1）所对应的正平衡点(D*,P*,S*)，当0≤τ＜τ0时，局部渐近稳定；当τ=τ0时，系统（1）在(D*,P*,S*)处产生Hopf分支；当τ＞τ0时，(D*,P*,S*)是不稳定的.

证明 系统（1）在(D*,P*,S*)的特征方程为

若令

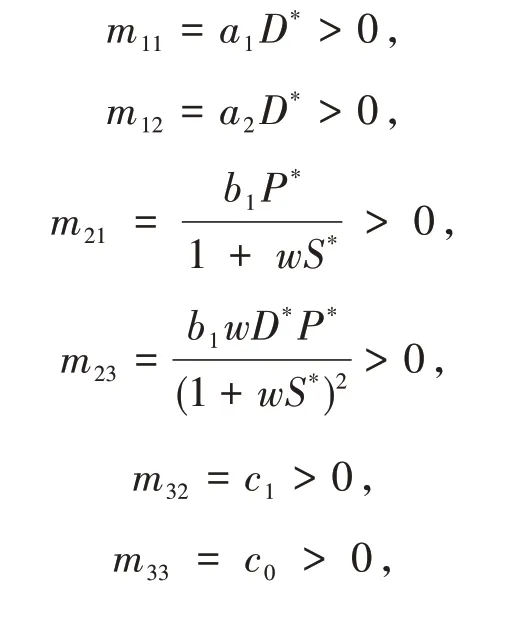
则有

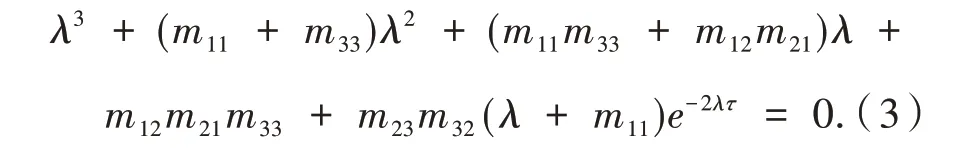
当τ=0时，系统（1）的特征方程（3）变换为

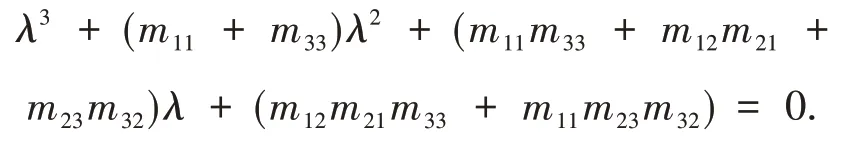
易知

根 据Routh-Hurwitz［8］定 理 知：特 征 方 程（3）的所有根具有负部，由Hurwitz［8］定理知：当τ=0时，正平衡点(D*,P*,S*)是局部渐近稳定的.

当τ＞0，设λ=ωi(ω＞0)是特征方程（3）的一纯虚根，则ω满足

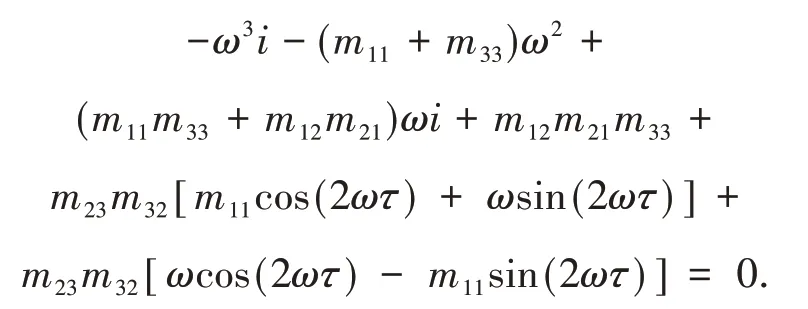
分离上式的实部和虚部可得

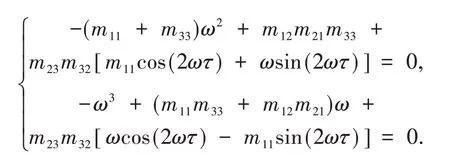
由上式可得

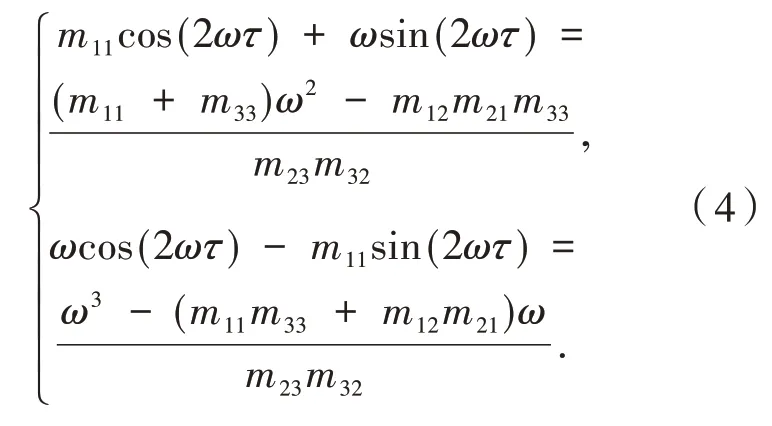
在式（4）中消去cos(2ωτ)，sin(2ωτ)，则有

因为条件H2成立，所以

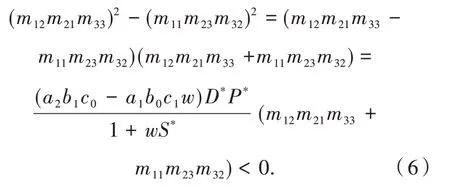
根据零点定理［12］，因此，方程（5）至少存在一正根ω0＞0，将其代入方程组（4）计算可得

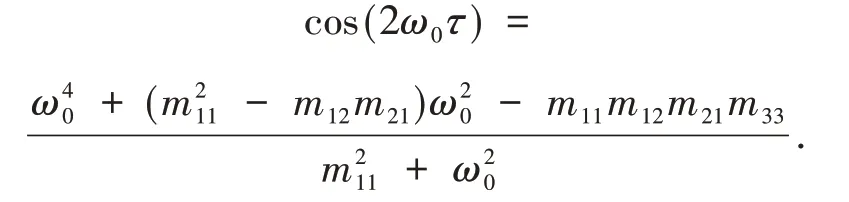
由上式可得与ω0对应的τn，

取τ0是式（7）产生纯虚根的最小正值.根据Butler引理可知：则当τ＜τ0时，正平衡点(D*，P*，S*)仍然保持稳定［13］.

令λ=λ(τ)，代入式（3），并在其两边对τ求导，有

将λ=ω0i，τ=τ0代入上式，得

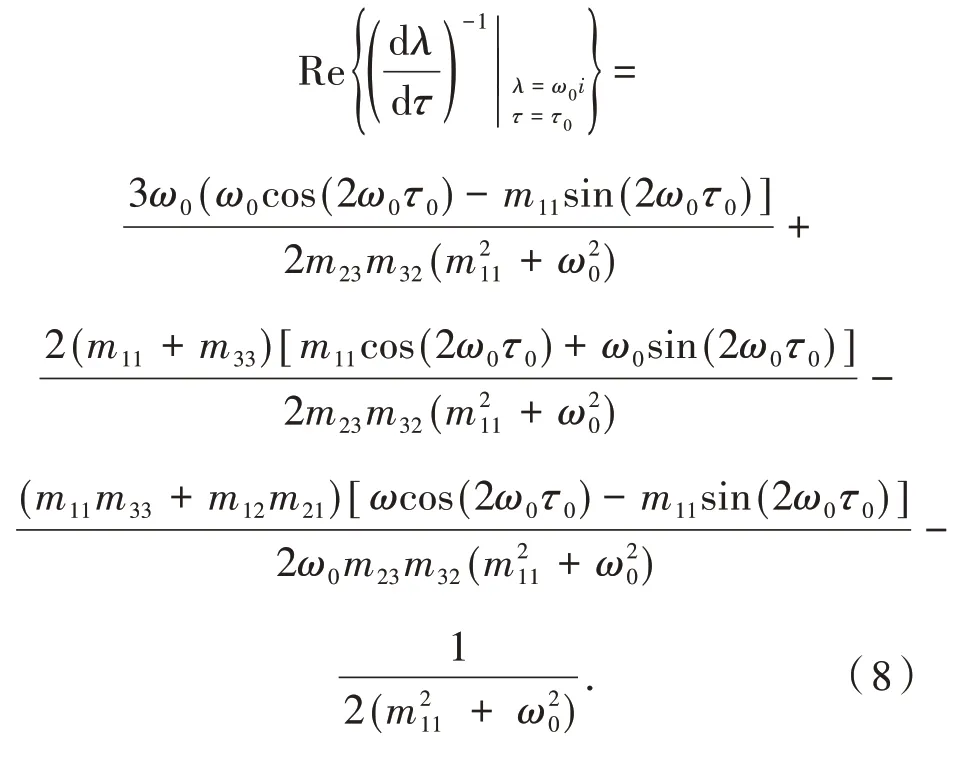
因为(ω0,τ0)是式（4）的解，因此有

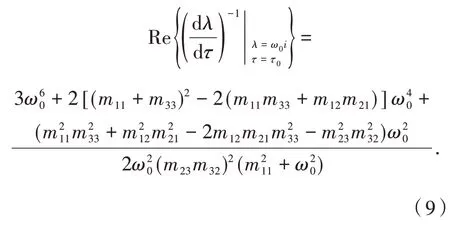
由式（5）可知

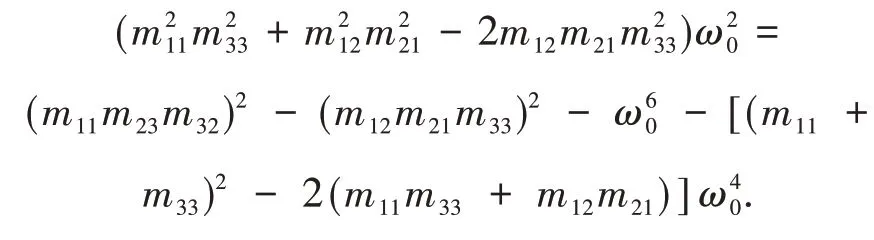
将上式代入式（9）可得

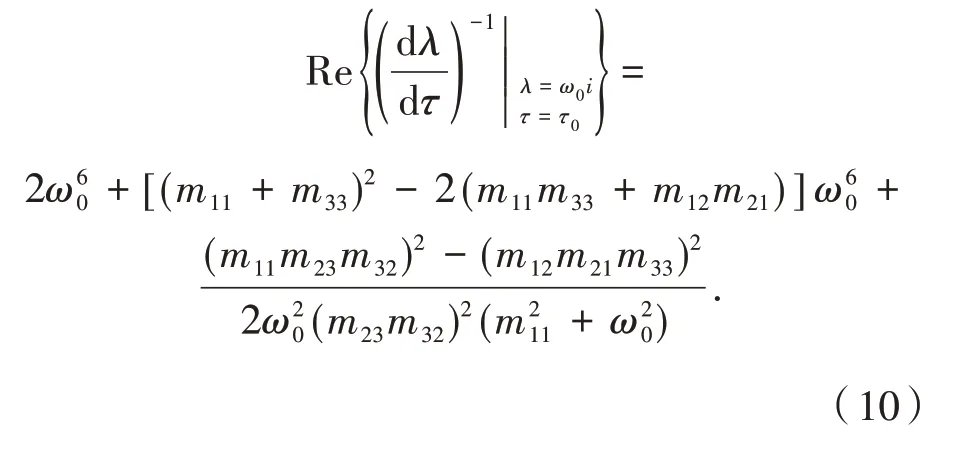
由式（6）可知(m11m23m32)2-(m12m21m33)2＞0.因为

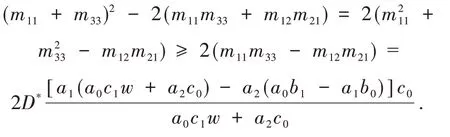
又因为条件H3成立，所以(m11+m33)2-2(m11m33+m12m21)≥0.综 上 可 得

由Hopf分 支 定 理 知，当τ=τ0时，系 统（1）在正平衡点(D*,P*,S*)产生Hopf分支；当τ＞τ0时，正平衡点(D*,P*,S*)不稳定［14-17］.

定理4分别给出了仅受生产周期影响的系统（1）在正平衡点(D*,P*,S*)局部渐近稳定和产生周期解的充分条件.

3 生产周期与猪瘟叠加效应影响下的猪肉商品动态关系分析

上文仅研究了生产周期对猪肉的供应量、价格和需求量的影响，若有瘟疫发生，则必定会对它们产生很大程度的影响［18-20］.为构建生产周期与猪瘟叠加效应影响下的猪肉商品关系模型，需作如下模型假设.

①当消费者得知有瘟疫发生时，必将会尽最大可能地降低需求，假设瘟疫发生时猪肉的最低需求量为常数d0(0＜d0＜D*).

②根据2018年非洲猪瘟的经验，瘟疫期间的肉类商品的价格接近最低值，接近于单位成本，假设此时的价格为最低值p0(0＜p0＜P*).

③瘟疫期间，为了阻止瘟疫地扩大，得病的生猪必须被处理掉，猪农几乎不会增加养殖量.因此，猪肉供应量就会出现断崖式下降，假设供应量的最小值为常数s0(0＜s0＜S*).

④当瘟疫影响结束时，供应量还需要一个生产周期才能提高.

为简化问题，假设tk(k=1,2,…)时刻瘟疫发生，tk+1时刻瘟疫影响结束.而在(tk-1,tk]时间段内，没有猪瘟影响.根据上面的分析与假设，生产周期与瘟疫叠加效应影响下的猪肉商品动态关系模型如下所示.

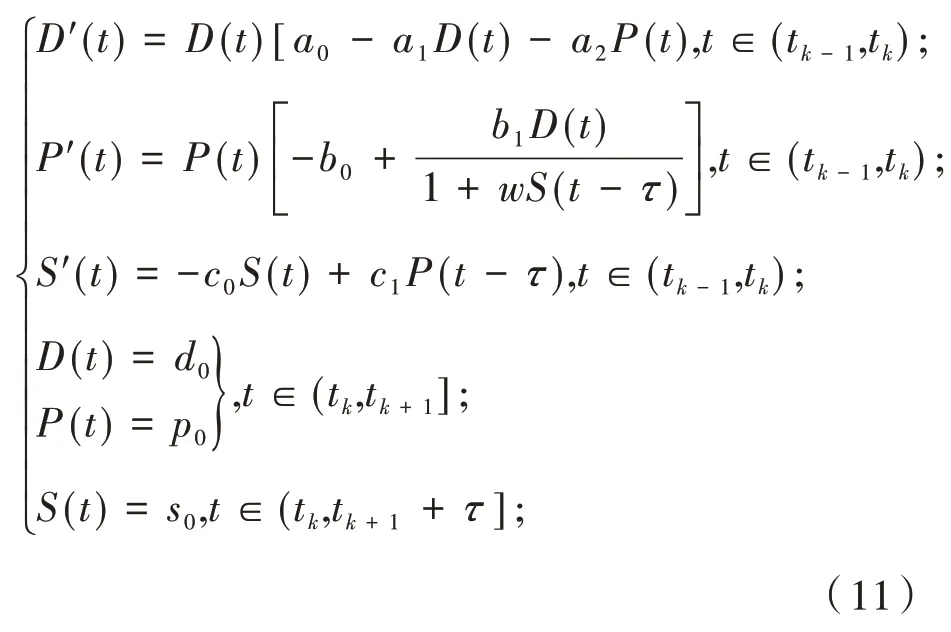
其 中 ：0＜t1＜t2＜…＜tk＜…＜tk+1+τ＜tk+2＜…，并且当k→+∞时，tk→+∞.

定理5当条件H4:a0-a1d0-a2p0＞0，H5:b1d0-b0-b0s0w＞0，H6:c1p0-c0s0＞0成立时，则有

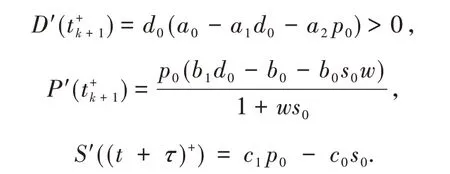
证明 根据导数极限定理［12］和系统（11）可知

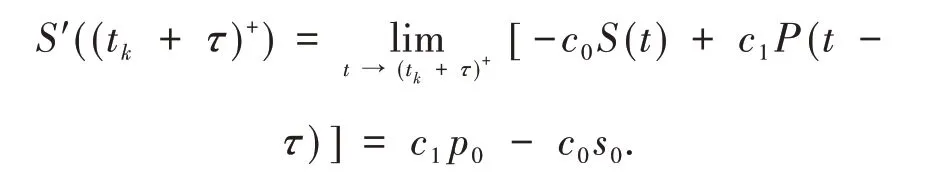
在瘟疫影响结束之后的第1个生产周期内，猪肉供应量仍然是s0，系统（11）等价于下面的系统（12）.

由系统（12）可得

若条件H4～H6成立，则有

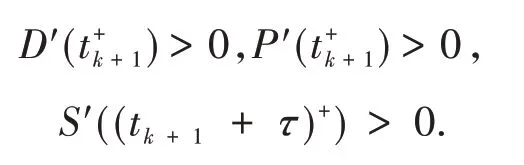
定理5给出了瘟疫影响结束时，需求量和价格的即时增速的数值.而S′((tk+1+τ)+)表示瘟疫影响结束之后第一个生产周期结束时的猪肉供应量的即时增速.

下 面 讨 论D(t)，P(t)在 区 间[tk+1,tk+1+τ]上的极值情形.根据命题“可导函数的极值点必为驻点［12］”的结论，求解方程

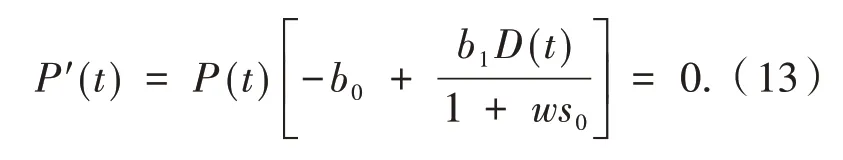
⑤tp是方程P′(t)=0的所有解中，在tk+1右侧并距离其最近的解.

⑥根据⑤的假设，若tp≥tk+1，则P(t)在(tk+1，tk+1+τ)内 无 极 值，所 以 需 假 设tk+1＜tp＜tk+1+τ.

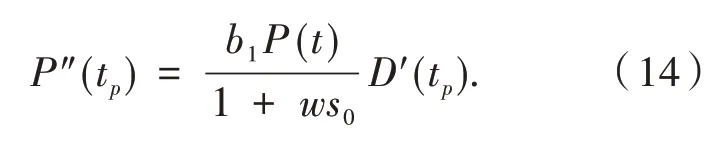
因此可得如下命题.

命题1若系统（12）满足条件H4～H6和假设⑤，⑥成立，则当D′(tp)＜0时，P(t)在tp点取得极大值；当D′(tp)＞0时，P(t)在tp点取得极小值.

命题1揭示，在瘟疫影响结束后的第一个生产周期内，猪肉价格随着需求量的增加而上涨.但是当需求量增加到极大值时，价格的上涨并未达到极大值，而是在需求量下降的某一时刻达到极大值.然后，价格会随着需求量的减少而降低，当价格降到极小值时，需求量也未达到极小值，价格是在需求量触底反弹之后的某一时刻达到极小值.

求 解 方 程D′(t)=D(t)[a0-a1D(t)-a2P(t)]=0，可得

⑦设td是 方 程D′(t)=0的 所 有 解 中，在tk+1右侧并距离其最近的解.

⑧同假设⑥中的原因，假设tk+1＜tp＜tk+1+τ.

因 为D″(t)=[a0-2a1D(t)-a2P(t)]D′(t)-a2D(t)P′(t)，所以D″(td)=-a2D(td)P′(td).进而可得如下结论.

命题2若系统（12）满足条件H4～H6和式（7），式（8）成立，则当P′(td)＞0时，D(t)在td点取得极大值；当P′(td)＜0时，D(t)在td点取得极小值.

命题2揭示，在瘟疫影响结束后的第一个生产周期内，猪肉需求量会在价格上涨过程中的某一时刻td达到极大值，也会在其价格下降过程中的某一时刻达到极小值.

4 数值仿真

在这一节，取相同的系数和不同的生产周期τ对系统（1）进行数值模拟.首先，取系数

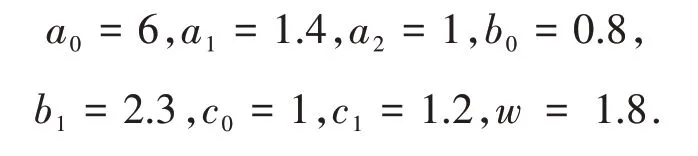
经计算，可验证上面的系数满足条件H1～H3.因此系统（1）的正平衡点和ω0,τ0分别为

取 初 值（D，P，S）=（1，1.5，1）.当 取τ=2＜τ0时，正平衡点是渐近稳定的.正平衡点（D*，P*，S*）局部渐近稳定的相图如图1、图2所示.

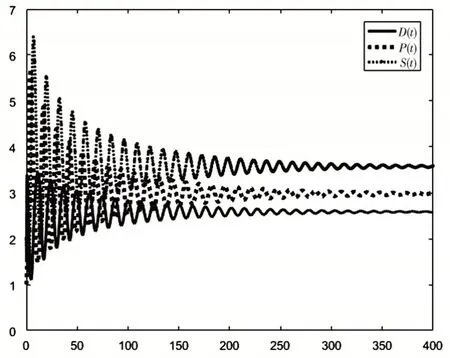
图1 正平衡点渐近稳定的平面相图

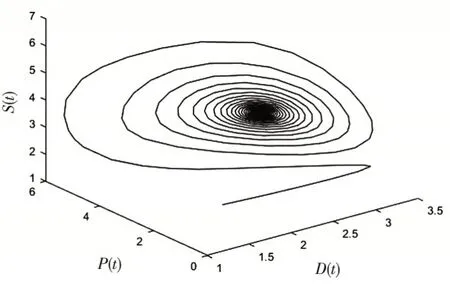
图2 正平衡点渐近稳定的三维相图

当取τ=5.3≈τ0时，系统（1）在正平衡点（2.37，2.69，3.22）处产生Hopf分支，即产生周期解，其相图如图3、图4所示.

图3 系统（1）存在周期解的平面相图

图4 系统（1）存在周期解的三维相图

再取时滞τ0=2.3，并取d0=1，p0=0.8，s0=0.6，易验证条件H4～H6成立.取瘟疫影响的时间段分别为［15，30］和［50，60］.数值仿真结果如图5所示.

图5 猪周期和猪瘟叠加效应影响下的数值仿真图

从图5可以看出，当瘟疫影响结束时，因为需求量的增率很大，所以它几乎是瞬时地变化到极大值，然后回归到正常的波动状态；在瘟疫影响结束时，价格也会以很快的速度攀升到极值点，但它的速率明显小于需求量的增长速率再回归到正常的波动状态.需求量与价格的快速升高与经济理论中的报复性反弹理论［14］比较贴合.

在图5中的两个区间［30，32.3］和［60，62.3］是瘟疫影响结束的第一个生产周期.在这段时间内，供应量（粗线表示）保持常数.需求量在价格（虚线所示）的上升过程中达到极大值，而价格（虚线所示）却是在需求量的下降过程中达到极小值.

2018年8 月，非洲猪瘟开始在我国蔓延，2019年，瘟疫影响基本结束.9月之后，随着需求量的恢复，猪肉价格一路飙升，至2020年初，价格开始平稳并逐步回落，这与图5中的仿真结果基本一致.

利用经济理论也可以很好地解释这种现象：在瘟疫影响结束后的一个生产周期内，供应量是固定的.因为需求量瞬时回归到正常状态，所以发生了严重的供不应求现象，因此价格会发生快速升高的现象.

5 结语

一般情况下，仅受生产周期影响的肉类商品会有两种变化趋势：一是需求量、价格和供应量动态波动地收敛于正平衡点；二是三者围绕正平衡点作周期性波动.当生产周期和瘟疫叠加影响肉类商品动态关系时也会有两种状况出现.瘟疫影响期间，需求量、价格和供应量均会降到它们的极小值；在瘟疫影响结束后的短期内，因为需求量极快地回升，导致严重的供不应求，所以价格升高的速度很快.