基于主成分分析的GA-BP神经网络地表下沉系数预测

郭凯维 郭传超 史耀凡 于 水

(山东科技大学 测绘与空间信息学院, 山东 青岛 266590)

0 引言

煤炭资源的不断开发能够带来巨大的社会经济效益,但也能够影响矿区生活环境,为保证煤炭资源开挖带来的持续效益以及减少煤炭资源开挖带来的负面影响,条带开采在我国矿区被广泛运用。条带开采通过对煤层采取开采一条、保留一条的方法,使得保留下的煤柱足以支撑上覆载荷,进而有效控制地表沉陷[1],而且不增加或减少正交生产成本,是“三下”(建筑物下、水体下、铁路下)煤层开采的有效手段之一。条带开采地表下沉系数是煤层开采地表沉陷预计中的一个重要参数,其取值的准确性会影响到地表移动变形计算和预计分析的精确度[2]。然而,影响地表下沉系数的因素十分复杂,存在着一定的相关性、不确定性以及非线性,难以用数学或力学的方法精确求取。目前,针对地表下沉系数难以求取的特点,众多学者引入非线性回归模型。郭文兵等利用BP神经网络(Back Propagation Neural Network)求取地表下沉系数[3],于宁锋等建立了粒子群法和向量机法相结合的地表下沉系数预测分析模型[4],赵保成等采用了基于随机森林算法的地表下沉系数求取方法[5]。条带开采地表下沉系数存在较多的干扰因素,并且存在冗余信息,直接对初始因素进行算法求取会降低预测模型精度,本文引用主成分分析法对原始数据进行预处理,降低原始数据维度并消除多余信息,进而使得模型网络结构更加简化;应用遗传算法对神经网络的初始权值与阈值进行优化,防止陷入局部最优值,提高预测准确性。结果表明,利用主成分分析法与GA-BP模型相结合可使预测精度更高,为地表下沉系数的求取提供了又一种方法。

1 相关理论

1.1 主成分分析

在统计分析多影响因素时,变量之间信息叠加使问题变得更为烦琐。主成分分析(Principal Component Analysis,PCA)是一种把变量之间互相关联的复杂性进行简化的统计分析方法,它能够在保留原始数据大部分信息的原则下,用较少的主成分对多变量进行最佳简化[6]。简言之,通过主成分分析既可以起到“降维”作用,又能保留原数据的大部分信息,便于问题的解决。主成分分析的具体步骤如下[7-8]:

(1)获取原始数据并对数据进行标准化处理;

(2)由标准化矩阵计算获得相关系数矩阵,求解相关系数矩阵的特征值和特征向量;

(3)计算主成分贡献率和累计方差贡献率,由累计贡献率达到80%～95%所对应的特征值个数确定主成分个数;

(4)建立主成分因子载荷矩阵,对主成分进行诠释。由此可得主成分分析的数学模型为

(1)

式中,Zp为原始变量的第p主成分;Xm为原始变量;apm为变量Xm所对应的载荷。

1.2 BP神经网络

BP神经网络因其研究起步早、理论完备,是目前应用最为广泛的多层前馈神经网络模型之一[9]。BP神经网络在非线性映射、自适应和自学习能力、泛化和容错能力等方面有着显著优势,被广泛应用于模式识别、预测评估等多个领域,并取得了许多突出成果[10]。

已有研究证实,一个三层的神经网络在理论上可以以任意精度与任意的连续函数相拟合。如图1所示,BP神经网络是一个含有输入层、隐含层和输出层的三层神经网络[11],其算法的具体步骤如下:

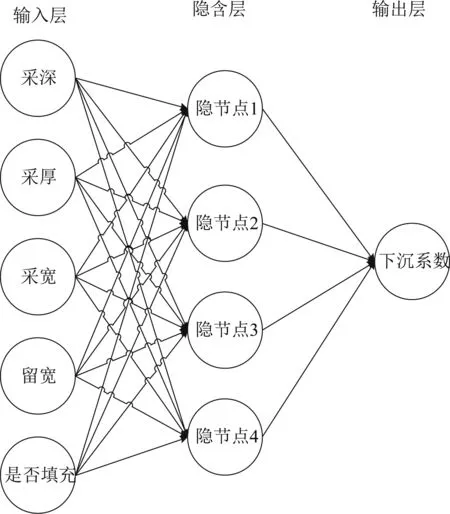
图1 三层BP神经网络结构图

(1)确定学习与测试样本,并进行归一化处理,消除数据间数量级的影响;

(2)初始化BP神经网络的权值与阈值,设置BP网络误差平方和;

(3)输入信号的正传播与误差逆传播;

(4)对权值与阈值进行更新;

(5)判断BP网络误差平方和是否满足条件。若满足,则迭代结束;否则,返回第(2)步,重复执行。

1.3 遗传算法

遗传算法(Genetic Algorithm,GA)是一种高效并行的随机全局搜索和优化算法。遗传算法具有群体搜索和随机搜索的特性,不易在寻优过程中陷入局部最优解,它可扩展性高,易于同别的技术相融合,在各个领域中都有着广泛应用[12]。

遗传算法的基本思想为:对于一个最优化问题,将问题中的候选解抽象为一个初始种群,借鉴进化生物学中的一些现象,如算法中的选择、交叉、变异、倒位操作,开始种群的繁衍,根据“优胜劣汰,适者生存”原理,以适应度函数为评价标准,对子代进行筛选,获取每一代中的最优个体,逐代演化直至产生最优个体。

2 改进BP神经网络模型的建立与应用分析

2.1 地表下沉系数影响因素选取与主成分分析

条带开采是一种减小地表移动变形造成的地面建筑物破坏的主要开采方法,其地表下沉系数是条带开采移动变形预计分析的关键性参数,大量实测数据与理论研究已经证明,条带开采地表下沉系数主要与以下因素有关:釆深、采厚、采宽、留宽、松散层厚度、煤层倾角、顶板管理方法等[13]。

由于矿区条带开采缺少对地表下沉系数影响因素的材料积累,现在仅对釆深、采厚、采宽、留宽、顶板管理方法五个影响因素进行分析。根据有关文献[14],获取国内外53个条带开采实例数据,以此运用“统计产品与服务解决方案”软件(Statistical Product and Service Solutions，SPSS)进行主成分分析。条带开采实例数据如表1所示,其中顶板全部垮落时用0表示,进行填充时用1表示。

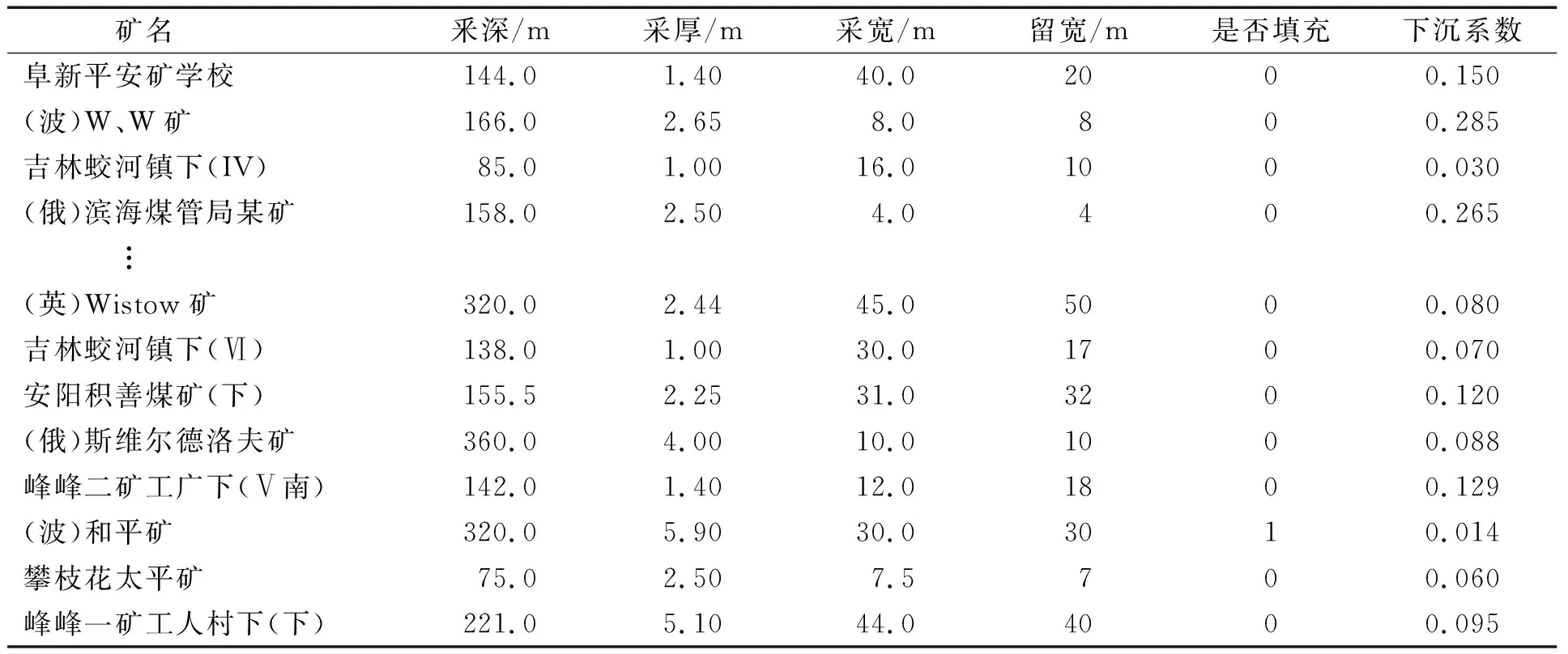
表1 训练与预测样本

KMO(Kaiser-Meyer-Olkin)检验值和Bartlett球形度检验值用来判断变量是否可进行主成分分析，当KMO在0.5以上且越接近1时就越适合做主成分分析。Bartlett球形检验值小于显著水平0.05或者0.01时，适合进行主成分分析。由表2可知：KMO>0.5，Sig<0.01。因此该例中各变量之间的相关性较大，存在信息重叠，符合降低数据维数的要求，可以用较少的主成分来代替较多的原始变量。

表2 KMO和Bartlett球形检验结果

主成分个数的选取可根据相关系数阵或协方差阵的特征值来确定。方差是各个变量数据所含有的信息重要判据之一,而在主成分分析中,相关系数阵或协方差阵的特征值与主成分的方差相等。由特征值决定主成分的数目的准则:特征值大于1;累计贡献率大于85%;由表3所示,根据累计贡献率大于80%准则可以得到该例的主成分个数为2。

表3 特征值贡献率

由表4中主成分系数可得主成分表达式为：

F1=0.567X1+0.158X2+0.551X3+0.581X4+0.114X5

F2=0.068X1+0.671X2-0.214X3-0.179X4+0.683X5

(2)

利用主成分表达式F1、F2计算标准化后的数据，将原始数据的5维变为2维,起到了降维作用,对改进BP神经网络的数据输入进行了简化处理。

表4 主成分系数

2.2 改进模型建立与预测

BP神经网络在非线性映射和容错能力等方面有着一定的优势,但在权值和阈值的初始优化方面缺陷较大,导致预测不够准确,为了克服这一缺陷,利用遗传算法在随机全局寻优中难以陷入局部最优解的优势,对BP神经网络的权值和阈值进行初始优化处理,提高BP神经网络预测未知样本的准确度。

利用遗传算法改进的BP神经网络简称为GA-BP模型,其主要思路包括BP神经网络结构的确定、遗传算法优化初始权值与阈值、模型预测[15-17],其计算流程如图2所示。采用MATLAB软件对基于主成分分析的GA-BP模型进行编程实现,以表1中的前45组数据为训练样本,后8组数据为预测样本。

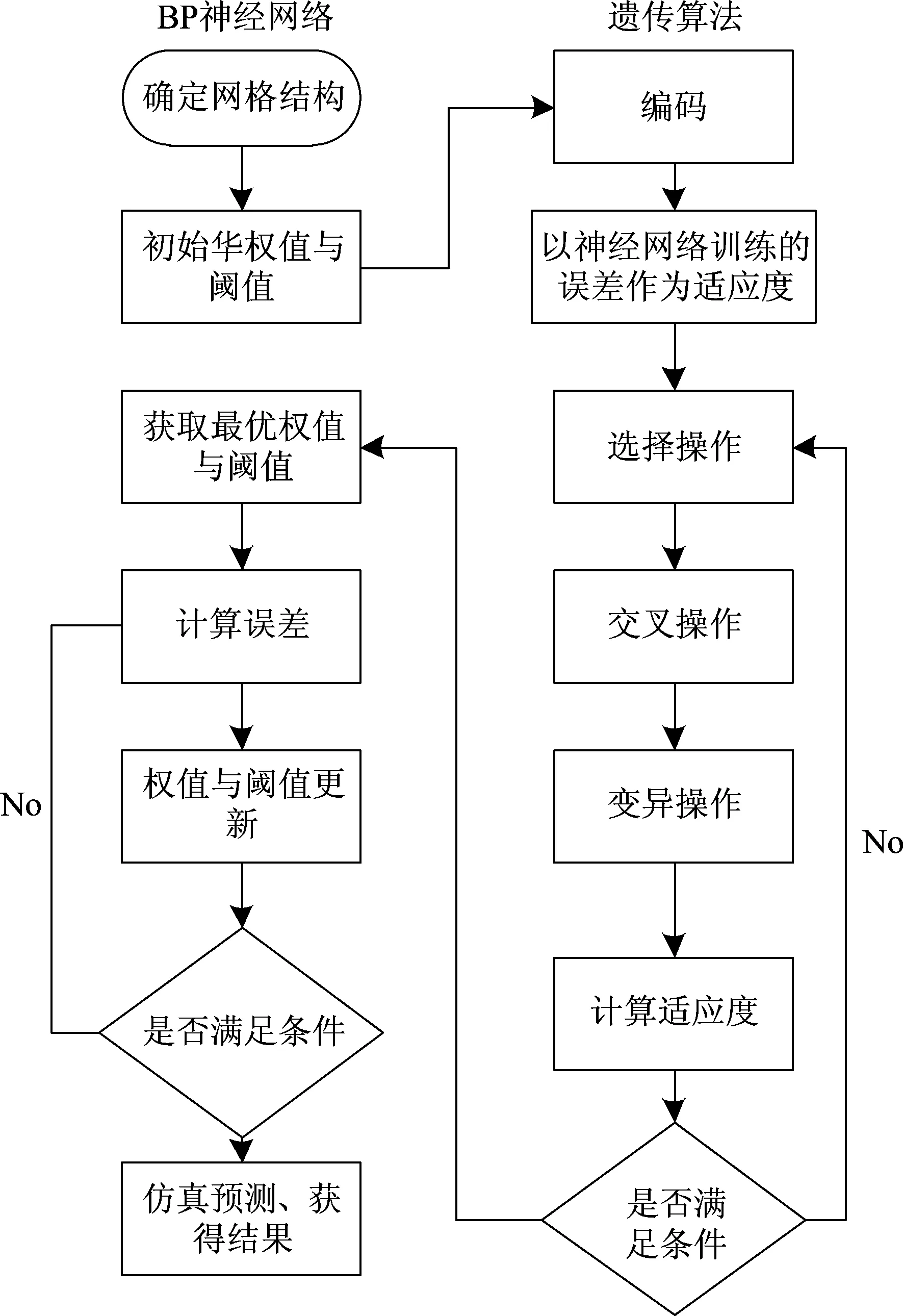
图2 GA-BP神经网络流程图

2.3 结果分析

为了进一步分析GA-BP模型的预测效果,构建了传统BP神经网络模型与PCA-BP模型,开展了三种模型用于条带开采地表下沉系数预测的性能对比研究。根据选取的参数,在MATLAB中进行仿真模拟获得输出结果,通过分析输出结果和实际测量值之间的误差是否满足要求来对比模型的预测效果及验证模型的精度与可靠性。不同模型的预测输出结果如图3所示,不同模型误差如表5所示。

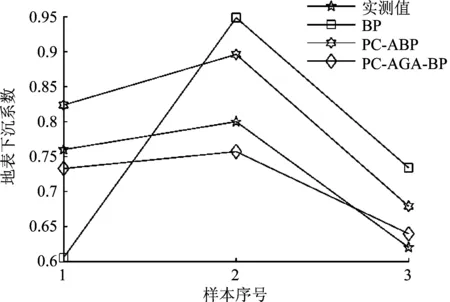
图3 不同模型的仿真预测结果

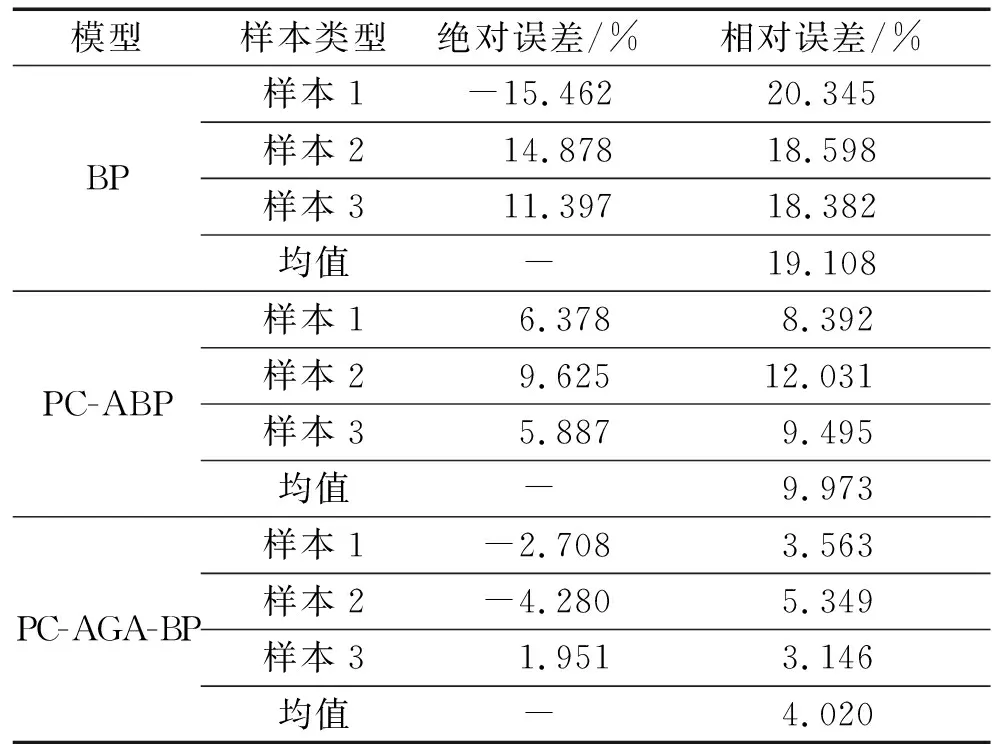
表5 模型误差

由图4可知,三种模型均能较好地拟合真实值,但PCA-GA-BP模型的拟合效果要优于其他模型,更为接近真实值。表5表明,BP神经网络模型的相对误差均值为19.108%,PCA-BP模型的相对误差均值为9.973%,这说明主成分分析降低了原始数据维度,消除了原始数据的冗余性,使得PCA-BP模型有着更好的预测精度。PCA-GA-BP模型的相对误差均值为4.020%,预测精度远高于BP模型,优于PCA-BP模型,这说明该模型的预测值与实测真实值更为吻合,精度更高,为求取地表下沉系数提供了一种准确可行的方法。

3 条带开采优化设计

由上述分析可知,GA-BP模型的预测效果与现场实测值更为吻合,可靠性高。现利用该模型进行条带开采优化设计,以优化条带开采尺寸为例,保持其他开采条件(釆深、采厚、采出率等)不变,通过比较不同采宽与留宽下的地表下沉系数来获得最佳的采宽与留宽。

以某矿区为例。该矿区煤层属于近水平煤层,平均釆深为960 m,采厚为1.95 m,用全部垮落法管理顶板。固定采出率为50%,根据矿区开采情况选取不同的开采方案,开采方案与相应的预测参数如表6和图4所示。

表6 下沉系数预测结果

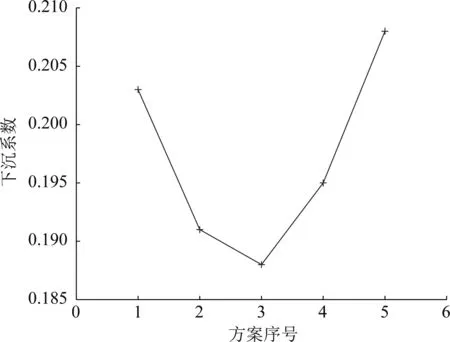
图4 不同方案的下沉系数

以条带开采地表下沉系数最小为原则进行条带开采优化设计,由计算结果可知,当采出率固定为50%时,方案3的地表下沉系数最小,能够更有效地减少地表移动变形,降低地表建筑物的破坏程度。

4 结束语

用SPSS20软件对原始数据进行主成分分析,数据维数由五维变为两维,起到了降维作用,简化了模型的输入参数。同时,在保留了原始数据的大部分信息的基础上,消除了各变量之间的相互影响,有利于提高模型预测的训练效率与精度。

基于主成分分析,构建了预测条带开采地表下沉系数的GA-BP模型。与传统的BP神经网络模型及PCA-BP模型相对比,由预测误差分析可知,基于主成分分析的GA-BP模型预测精度可达到3%,远优于其他模型,因此,具有更高的利用价值。利用该模型进行了条带开采优化设计,通过对比不同的采宽与留宽,在保证地表下沉系数最小的前提下,获得最优的采宽与留宽,这对优化条带开采尺寸起着重要的参考作用。

模型的预测精度受样本容量的影响很大,又因为地表下沉影响因素的实测数据缺乏,所以该模型的预测精度有待进一步提高。随着煤矿开采资料的积累,该模型的预测结果将更为可靠,利用价值也有着更高的提升空间。