精密三角高程测量在大藤峡水利枢纽左右岸高程联测中的应用

黎建洲，张金生，曹 浩，刘 源，李立平，胡 蕾

(1.长江科学院 工程安全与灾害防治研究所，武汉 430010； 2.水利部水工程安全与病害防治工程技术研究中心，武汉 430010； 3.国家大坝安全工程技术研究中心，武汉 430010； 4.广西大藤峡水利枢纽开发有限责任公司， 南宁 530200)

1 研究背景

在跨河水准测量时，《国家一、二等水准测量规范》中规定，当跨河视线长度超过100 m时，跨河水准测量的主要方法有光学测微法、倾斜螺旋法、经纬仪倾角法、测距三角高程法和GPS测量法[1]。三角高程测量是跨河水准测量中一种应用比较广泛的技术，其基本思想是根据由已知高程点向目标待测点观测所得的竖角(或天顶距)和距离，计算两点间高差，从而进行高程的传递，其精度主要受到观测仪器精度、大气折光、地球曲率和垂线偏差等因素的影响[2-4]。

随着高精度测量机器人(测角精度0.5 s，测距精度0.6 mm±1 ppm)的出现，通过对仪器的加装和改进测量方法，利用2台测量机器人同时对向观测，可以大大削弱大气折光的影响，并且无需量取仪器高和目标高，避免了该项测量带来的误差，能够达到国家二等水准测量精度的要求。刘冠兰等[5]在宽水域跨河水准中利用精密三角高程测量，测量结果内符合和外符合精度都满足二等水准测量精度要求；徐亚明等[6]利用一种改进的三角高程法进行跨海高程传递，提高了作业效率，精度达到二等水准要求；郝旦等[7]采用四边形跨河水准测量方法进行精密三角高程传递，通过实例证明该方法能满足二等跨河水准测量精度要求。

2 精密三角高程测量方法

2.1 测量原理

精密三角高程测量是在传统三角高程的基础上，采用2台带有自动照准功能(ATR)的高精度测量机器人，通过加装，将目标棱镜固定在测量机器人的手柄上，保证棱镜中心与仪器中心同轴，如图1(a)所示。2台仪器同时对向观测，可以大大削弱大气折光的影响。起点和终点采用同一根固定高度的棱镜杆，如图1(b)所示，且保证对向观测测段数为偶数，计算中抵消了仪器高和棱镜高，避免了该项量高误差。

图1 仪器及棱镜改装Fig.1 Modification of instrument and prism

2.2 测量流程

精密三角高程的测量流程如图2所示，具体测量步骤如下。

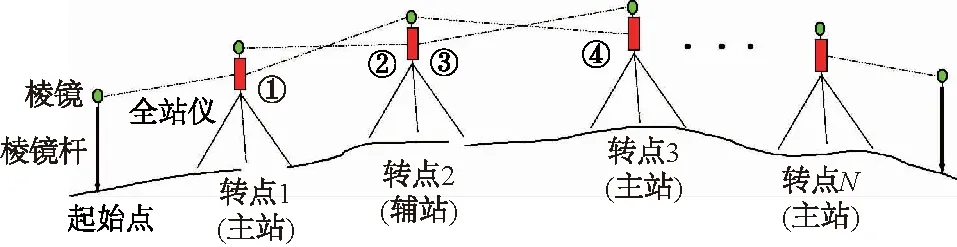
图2 精密三角高程测量流程Fig.2 Flow chart of precise trigonometric leveling

(1)在测段起始点上架设固定高度的棱镜杆，在距离起始点5～20 m的合适的位置(转点1)，架设仪器(称为主站)，主站观测起始点上的的棱镜。

(2)主站位置不动，在转点2位置架设另一台仪器(称为辅站)。依次进行如下观测：后测站观测前测站上的棱镜①，前测站观测后测站上的棱镜②。

(3)辅站不动，主站搬站到转点3位置。依次进行如下观测：后测站观测前测站上的棱镜③，前测站观测后测站上的棱镜④。

(4)主站不动，辅站搬站。重复步骤(3)和(4)，将高程传递至接近测段终点处(距离终点5～20 m)，保证对向观测测段为偶数。

(5)将同一根固定高度的棱镜杆架设在终点上，主站观测终点上的目标棱镜。完成该测段测量。

3 精密三角高程测量误差分析

根据精密三角高程测量的流程，可以看出，测量分为起、末点仪器单向观测棱镜杆和中间转点仪器对向观测2种模式。分别分析这2种测量模式的高程传递方程。

3.1 起、末点仪器单向观测棱镜杆观测方程

如图3所示，仪器和棱镜杆所在位置的高程分别为h1和h0，根据佩利年于1978年在《理论大地测量学》一书中提出的单向观测高差计算的严密公式可得[8]

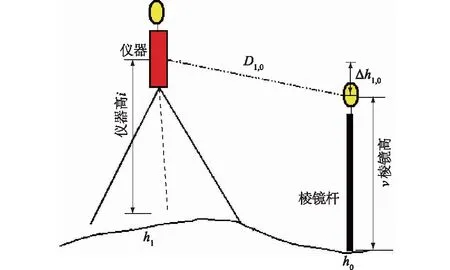
图3 起、末点仪器观测棱镜杆Fig.3 Prism rods of observation instrument at startingand ending points

(1)

式中：D1，0为仪器观测棱镜的斜距；Z1，0为仪器观测棱镜的天顶距；i为仪器高；v为棱镜高；ρ为孤度对应的秒值，取值206 265;ε1为照准方向上的垂线偏差分量；εc为计算两点高程异常之差时垂线偏差的积分值；K1为仪器到棱镜的大气折光系数；S为经气象改正后的斜距在参考椭球上的投影边长；R为两点的平均曲率半径；a为参考椭球的长半轴；e为参考椭球的第一偏心率；B1、B0、Bm分别为仪器和棱镜所在位置的纬度和平均纬度。

3.2 仪器对向观测方程

如图4所示，主站和辅站所在位置高程分别为hn-1和hn，ΔP1、ΔP2分别为主站和辅站加装棱镜中心至仪器中心的距离，可以得到主站仪器中心到辅站仪器中心的高差Δhn-1,n为

(2)

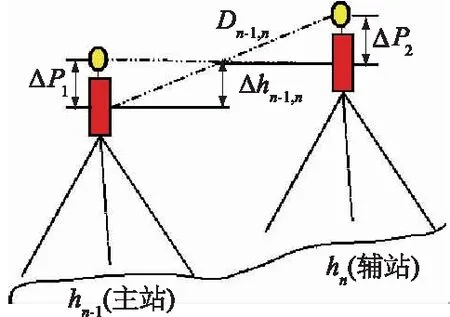
图4 对向观测Fig.4 Opposite observation

式中：Dn-1,n、Zn-1,n分别为主站仪器观测辅站棱镜的斜距和天顶距；Dn,n-1、Zn,n-1为辅站仪器观测主站棱镜所获得的斜距和天顶距；εn-1、εn分别为2台仪器照准方向上的垂线偏差分量；Kn-1、Kn分别为2台仪器分别到棱镜的大气折光系数。

3.3 精密三角高程观测方程

根据上述推导的起、末点仪器单向观测棱镜杆和中间转点仪器对向观测2种模式的观测公式，当n为偶数时(对向观测边为偶数)，起点高程和终点高程分别为H0和Hn，则有

Dn-2,n-3cosZn-2,n-3)+Dn-1,ncosZn-1,n]+

(3)

由式(3)可以看出，第一项通过观测值可以计算出测段的概略高程，第二项为对向观测的改正项，最后三项为起、末点仪器单向观测棱镜杆的改正项。通过缩短起、末点仪器观测棱镜杆的距离、增加测回次数等方法，起、末点仪器单向观测棱镜杆短边的改正项可以忽略不计[9]。对向观测边几乎同时进行观测，大大削弱了大气折光的影响，且完全消除了地球曲率的影响[10]。因此，在忽略大气折光、垂线偏差和地球曲率的影响下，精密三角高程测量的精度主要由仪器的测量精度和观测时的天顶距、斜距的大小共同决定[11]。在实际测量中，应该控制好仪器的高度角和测量距离，提高精密三角高程的测量精度。柏文峰等[12]通过大量试验，解算得到精密三角高程测量每公里的观测中误差约为±2 mm，能够满足国家二等水准测量规范的需要。

4 工程实例

4.1 工程概况

大藤峡水利枢纽工程是国务院批准的珠江流域防洪控制性枢纽工程，也是珠江—西江经济带和“西江亿吨黄金水道”基础设施建设的标志性工程，水库总库容为30.13亿m3，防洪库容和调节库容均为15亿m3，电站装机容量1 600 MW，多年平均发电量72.39亿kW·h。大藤峡水利枢纽工程是具有防洪、航运、发电、补水压咸、灌溉等功能的流域关键性工程。

大藤峡水利枢纽工程变形监测控制网由平面监测控制网和水准监测控制网两部分组成。水准监测控制网由左岸的3个基准点、30个水准工作基点和右岸的12个水准工作基点，共计45个水准点组成水准监测控制网，每年按照《国家一、二等水准测量规范》中一等水准技术要求进行复测。大藤峡水利枢纽左岸工程于2015年9月开工，2020 年 3月左岸开始下闸蓄水，右岸工程于2019年10月开始施工。右岸需要对施工期边坡进行变形监测，确保边坡的稳定性。右岸的水准工作基点目前位于施工变形区域内，为了判断右岸水准工作基点的稳定性，需要从左岸的水准基准点通过交通桥与右岸水准工作基点按照二等水准技术要求进行联测。几何水准测量是用水准仪和水准尺测定地面上两点间高差的方法，在地面两点间安置水准仪，观测竖立在两点上的水准标尺，按尺上读数推算两点间的高差，通常由水准原点或任一已知高程点出发，沿选定的水准路线逐站测定各点的高程，如图5所示。

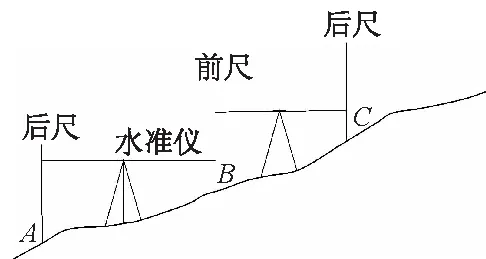
图5 几何水准测量Fig.5 Geometric leveling

目前，大藤峡水利枢纽左右岸高程联测采用传统的几何水准测量方法，主要有以下4个特点：

(2)时效性要求高。大藤峡水利枢纽右岸正处于施工高峰期，右岸水准工作基点沉降尚未稳定，高程值需要及时更新，便于指导右岸施工。

(3)测量线路长。大藤峡水利枢纽左右岸高程联测整个测量线路长约2 km，测段中间均位于交通桥上，无法设置中间转点。

(4)受环境干扰较大、测量效率低。交通桥上白天有很多重型施工车辆通行，车辆通过会引起桥梁的晃动，使二等水准测量经常无法正常读数，且数据质量较差导致往返测较差超限。现场实际测量通常是选择晚上车辆较少的时候，人工辅助照明，分上、下半夜不同时间段进行往返测。

采用精密三角高程测量方法可以不受交通桥的影响，简化作业过程，提高作业效率。

4.2 测量实施

利用精密三角高程测量方法，如图6所示，进行大藤峡水利枢纽工程左岸水准工作基点BM10与右岸水准工作基点BM11的跨河水准联测。利用2台徕卡TM50全站仪按照2.1节的方法加装徕卡圆棱镜，控制起、末两条短边距离约为5 m，按照2.2节的测量流程进行跨河水准测量，完成往测；测量完成后交换主站和辅站的仪器，再次进行测量，完成返测。测量过程中质量控制要求见表1。

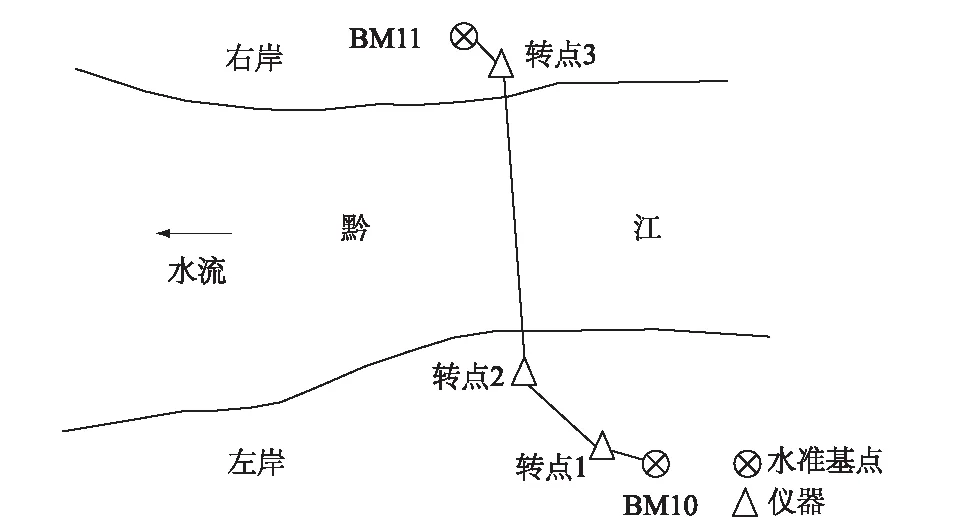
图6 大藤峡左右岸高程联测Fig.6 Joint elevation survey of left and right banksof Datangxia project

表1 精密三角高程测量质量控制Table 1 Quality control of precise trigonometric leveling

4.3 结果分析

大藤峡水利枢纽左右岸高程联测时天气晴朗，视线范围内能见度高，没有阳光直射仪器，水汽较少，左右岸气压一致，温度相差0.2 ℃。往返测均观测8组，每组8测回，每组高差观测数据见表2。

表2 高差结果对比Table 2 Comparison of height results

《国家一、二等水准测量规范》中规定，二等水准测量的每千米高差全中误差Mw为2 mm，跨河测段距离为L(km)，高差测量中误差限差为

(4)

本次测量结果取8组测量的平均值，则每组测量的中误差限差为

(5)

两组之间差值的限差为

(6)

本次测量测段BM10—BM11长约1.7 km，8组高差平均值为3.322 1 m，根据式(4)—式(6)计算出来的测量不确定度与限差值进行对比，见表3。

表3 测量不确定度与限差对比

将精密三角高程测量往返测较差，和几何水准测量结果对比，见表4。

表4 测量结果对比Table 4 Comparison of measurement results

从表3和表4可以看出，精密三角高程测量不确定度满足限差要求；往返测高差较差为0.6 mm，满足二等水准往返测限差要求；与几何水准测量结果相比较差为1.0 mm，满足二等水准检测已测测段高差之差要求。说明利用精密三角高程测量进行大藤峡水利枢纽工程左右岸高程联测，其结果达到二等水准测量要求。

通过现场实际测量，精密三角高程测量与传统几何水准测量相比有以下优势：①效率高，大藤峡水利枢纽工程左右岸跨河水准联测，实际往返测量共耗时2 h，传统几何水准测量则需要一整晚，工作效率得到了很大的提高；②受外界环境干扰小，精密三角高程测量只需要左右岸气象条件稳定，就可以正常测量。

5 结 语

精密三角高程测量利用2台高精度全站仪对向观测，削弱大气折光的影响，改进测量方法，避免仪器高和目标高的测量误差。通过三角高程计算的严密公式，从理论上推导了精密三角高程测量的误差公式，并在大藤峡水利枢纽工程左右岸高程联测中实际应用，与水准测量结果进行对比，达到二等水准测量精度要求。

该方法也存在一些问题：对仪器设备要求较高，同时需要2台高精度测量机器人，且要对仪器进行棱镜加装；对向观测边两端气象条件要求较稳定，后续可以研究对跨河边长进行气象条件模型改正。该方法设站灵活，工作效率较几何水准测量有很大的提高，且精度能够满足二等水准测量要求，在类似跨河水准高程传递中具有很好的借鉴意义。