追本溯源 深度思维
——对一道中考模拟压轴题的思考
2022-01-23朱佳炜江苏省苏州大学实验学校215131
朱佳炜 (江苏省苏州大学实验学校 215131)
周正峰 (江苏省苏州相城区教育局教研室 215131)
压轴题因为文字量大,需要耐心阅读、认真审题,拨开出题者设置的思维迷雾,厘清本题涉及的数学知识点和基本模型.在教学过程中我们应引导学生层层递进,学会如何思考、解决问题,在此基础上进行拓展研究,让学生知道压轴题是什么,该怎么想,怎么做,还可以怎么样.
1 试题呈现
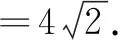
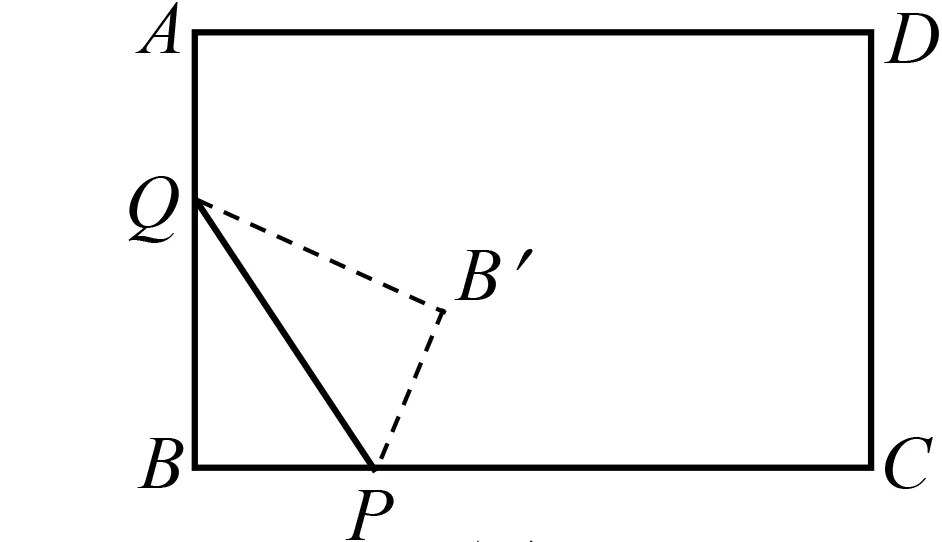
图1
(1)当t=1时,PQ=.
(2)连结AC,若点B′正好落在线段AC上,求t的值.
(3)点B′能否落在AD所在直线上,若能,求出AB′的长度;若不能,请说明理由.
2 题情分析
本题满分12分,区均分2.85分,得分率为23.75%,其中问题(1)满分2分,也就是说本题多数学生只能解答出问题(1).出现这一情况的根本原因在于学生不会对“点P与Q分别沿着各自方向运动,沿PQ所在直线翻折,点B′正好落在线段AC上”所对应的状态进行准确作图,个别学生因在问题(2)中对“点Q沿B-A-D方向运动”进行了分类讨论,耗费大量时间,影响了问题(3)的作答,导致本题得分率偏低.
3 解法探究
3.1 求证相似,追问溯源
从关键条件出发,证得相似三角形,再根据相似性质列方程求解.
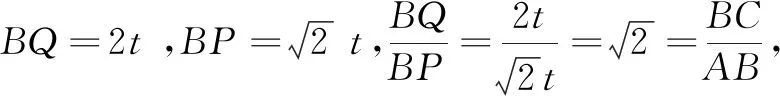
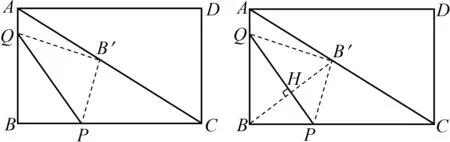
图2 图3
通过面积法或相似性质求得BH:
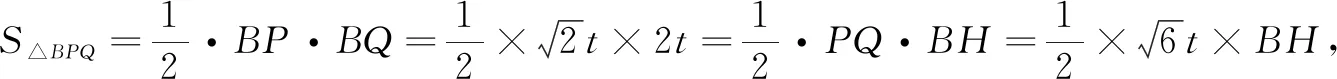
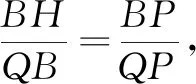
追问:当点Q在BA上运动时,B′可以落在AC上几次?
溯源:因为∠B′BC=∠BCA,所以∠B′BC是定角,而且边BC为定边,点B′将在以点B为端点的定射线上运动,该射线与AC只有一个交点,该交点即为B′,所以问题(2)中的t只有一解.
3.2 构建模型,灵活解答
抓住∠QB′P=90°,展开充分联想,构建基本模型“K”形图.
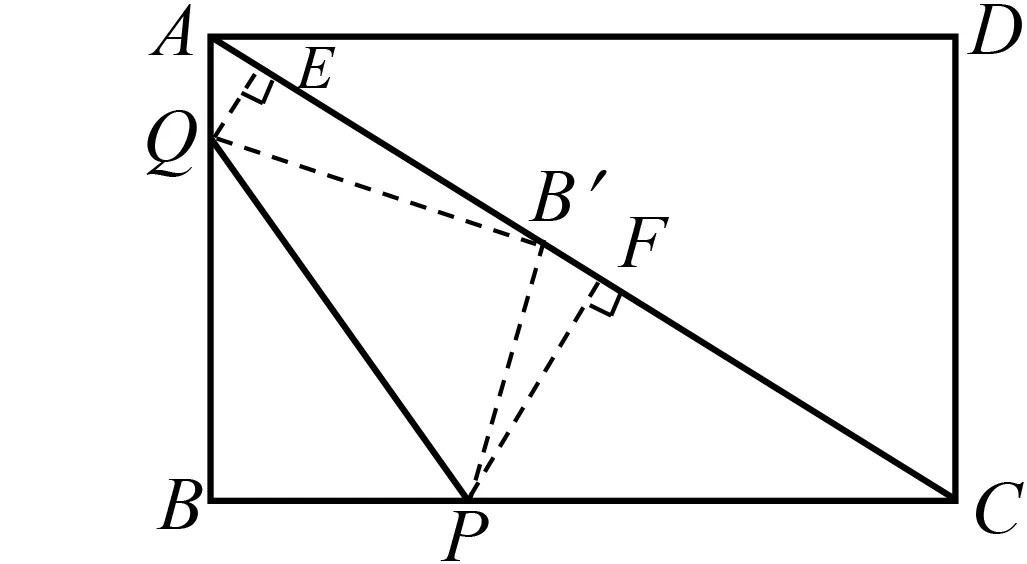
图4

追问:试探究AE与B′F、EB′与FC的数量关系.
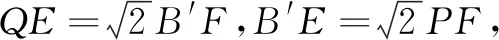
3.3 建系化归,数形结合
建立直角坐标系,将几何问题转化为函数问题,将坐标代入函数解析式求值.
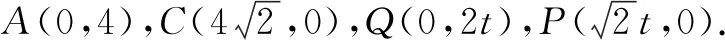

图5 图6
追问:点B′随着点P与点Q的运动而运动,该点的运动轨迹是什么?
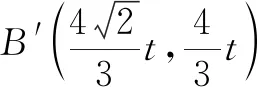
3.4 基于经验,思维突破
在问题(2)顺利解答的基础上,我们进一步探究问题(3).问题(3)中点B′落在AD所在直线上,所对应的点P、点Q所在位置需进行分类讨论.
当点Q在B-A运动时,通过作图发现点B′只能在矩形内部运动(图7),所以当点B′落在AD所在直线上时,点Q在A-D运动(图8).
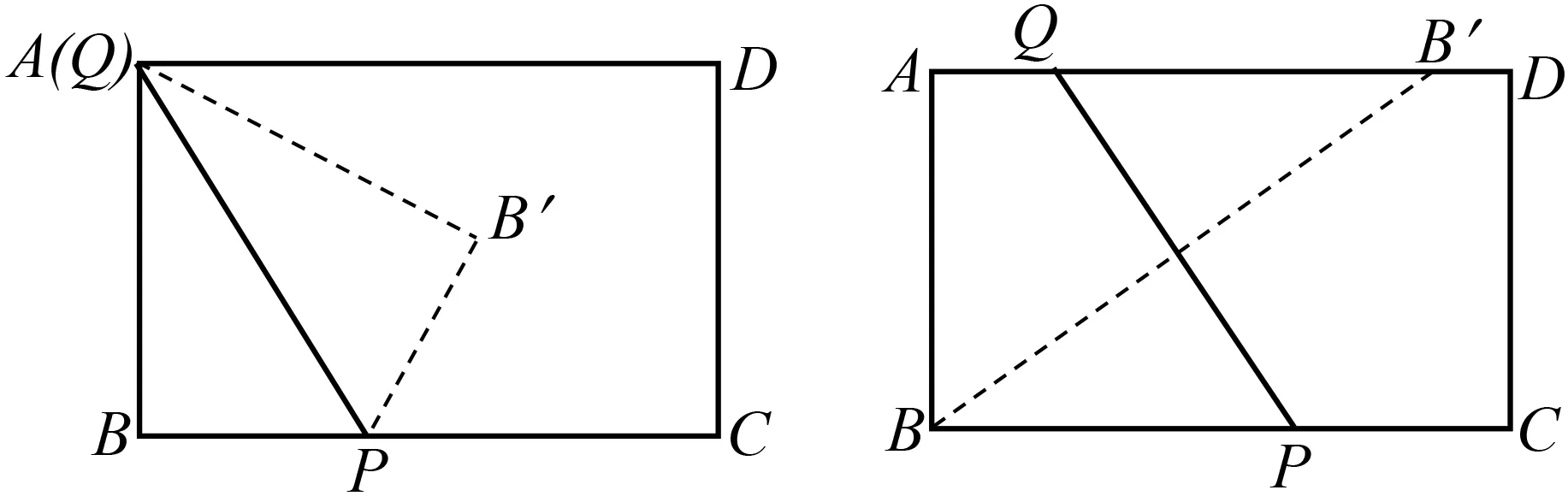
图7 图8
那么,点Q在A-D运动时,如何求AB′的长度呢?
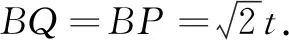
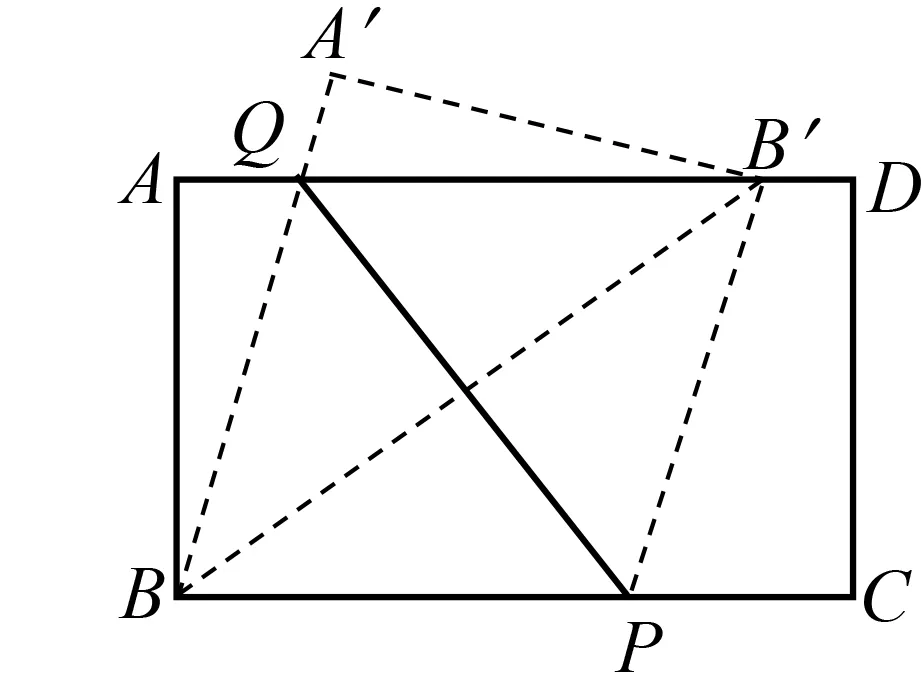
图9
追问:当点Q在A-D运动时(图10),在翻折的过程中,点B′能否落在点Q左侧,即QA射线上?

图10 图11
溯源:因为vP 时,点Q将在水平方向上逐渐超过点P,沿着PQ翻折所得点B′将落在PQ的右下方(图11),所以点B′不可能落在QA射线上. 例1解决了让学生知道压轴题“是什么、该怎么想、怎么做”等问题.与“翻折”有关的压轴题还能以什么形式呈现?讲解完例1后,进行了以下拓展研究. 例2如图12,在矩形ABCD中,已知AB=3,BC=4,E是BC边上一点,连结AE,将点B沿AE折叠得点B′ .当△CEB′ 为直角三角形时,求BE的长. 图12 本题的关键条件是“△CEB′为直角三角形”,而直角三角形的定义是一个内角为直角的三角形,本题必然要分三种情况进行讨论. 若∠CEB′=90°,那么四边形ABEB′中有三个角为直角:∠B,∠AB′E,∠BEB′,易证四边形ABEB′为正方形.若∠CB′E=90°,那么∠CB′E+∠AB′E=180°,则A,B′,C三点共线,运用勾股定理求解即可;若∠ECB′=90°,那么B′在CD边上,不合题意,舍去. 追问:为什么当∠ECB′=90°时,不合题意?若将“AB=3,BC=4”改为“AB=4,BC=3”呢(图13)? 图13 图14 溯源:翻折不改变AB长度,由“定点定长型隐形圆”可知,B′点在以A为圆心、AB长为半径的圆上运动,该圆与CD相离,所以B′不可能落到CD边上(图14),∠ECB′=90°不合题意.将“AB=3,BC=4”改为“AB=4,BC=3”,则⊙A将与CD相交,所以第三种情况符合题意(图15). 图15 为进一步激发学生思维,可以追问:若“E是BC边上一点”改为“E沿着射线BC运动”,是否还有其他情况符合题意?学生由圆与直线相交的定义可知⊙A与直线CD的交点有两个,所以存在第四种情况. 中考考试前如何组织高效的数学复习?首先,数学题目千千万,不能依靠刷题提高数学解题能力,应基于学生的知识基础,在课前精选好题.什么是好题?好题的解题方法不唯一,题目虽新但似曾相识,它一定源于平时的学习,可将它与已有的解题经验建立联系,进行合情推理.其次,压轴题通常是综合性较强的题目,已知条件多,特别是部分关键条件隐含在题目中,在教学过程中应帮助学生分析题目已知,挖掘隐含条件,并由关键条件出发寻找解题策略.再次,要通过多角度研究,尝试多种数学方法,让学生感悟数学思想.数学思想是数学课堂的灵魂,若只讲解法不谈思想,那数学课堂必然是乏味的.数学题目的背后一定蕴藏着数学思想,如转化化归思想、分类讨论思想、建模思想等.最后,要适度追问,挖掘思维深度,追本溯源,拓展思维.除了要让学生知道中考压轴题“是什么、该怎么想、怎么做”以外,应引导学生思考这样的题目“还可以怎么样”,是否可以换一种形式呈现.也就是说,中考考前复习课不能满足于一题的解决,还应结合关键条件进行类题探究,以激发学生的创新意识. 总之,在压轴题的教学过程中,应基于学生的知识经验、解题经验,引导学生整合、化归,在联想中合情推理,在追问中实现溯源,在拓展中获得延伸,在感悟中走向深刻.让中考复习课成为有灵魂、有创新、有深度的课堂.4 类题再探

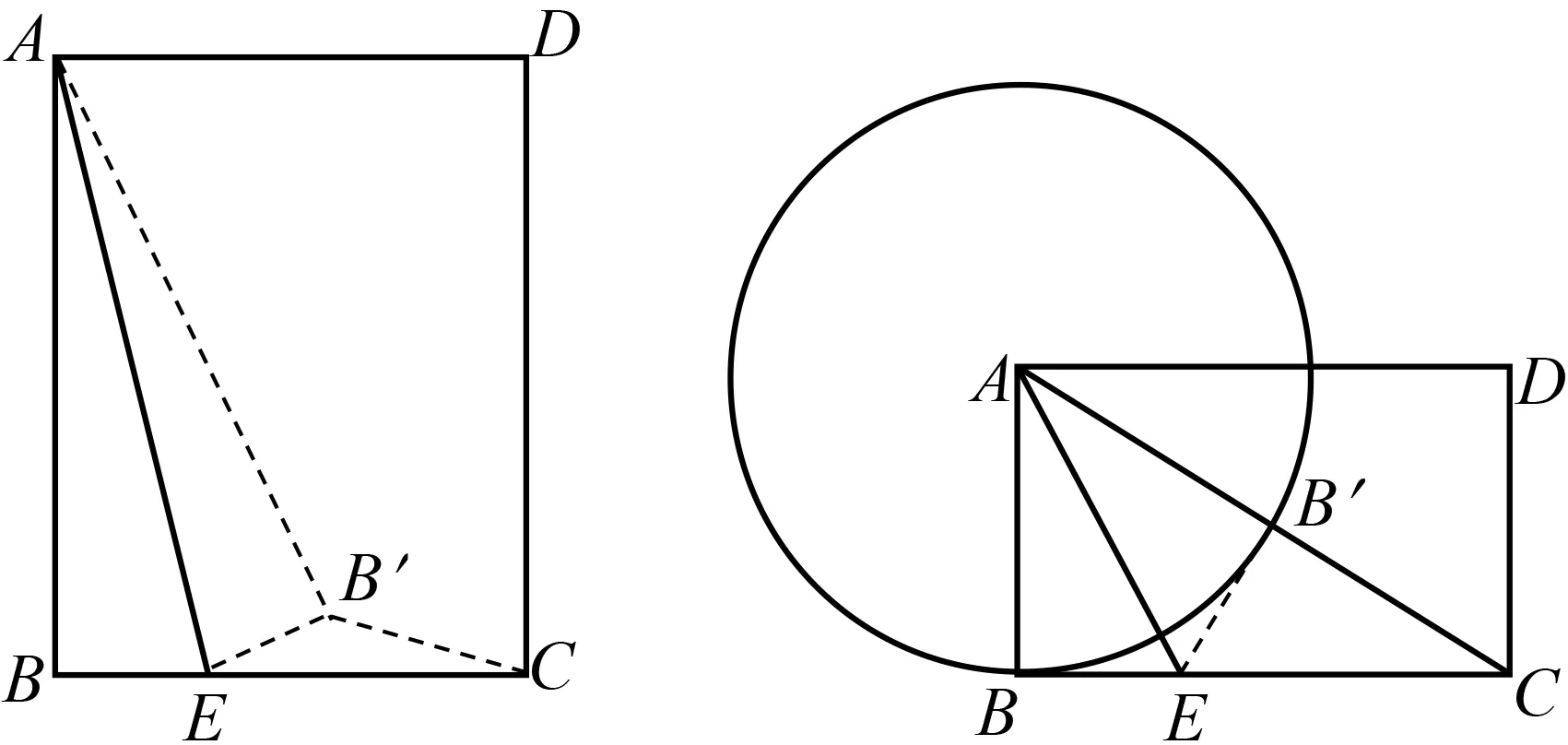
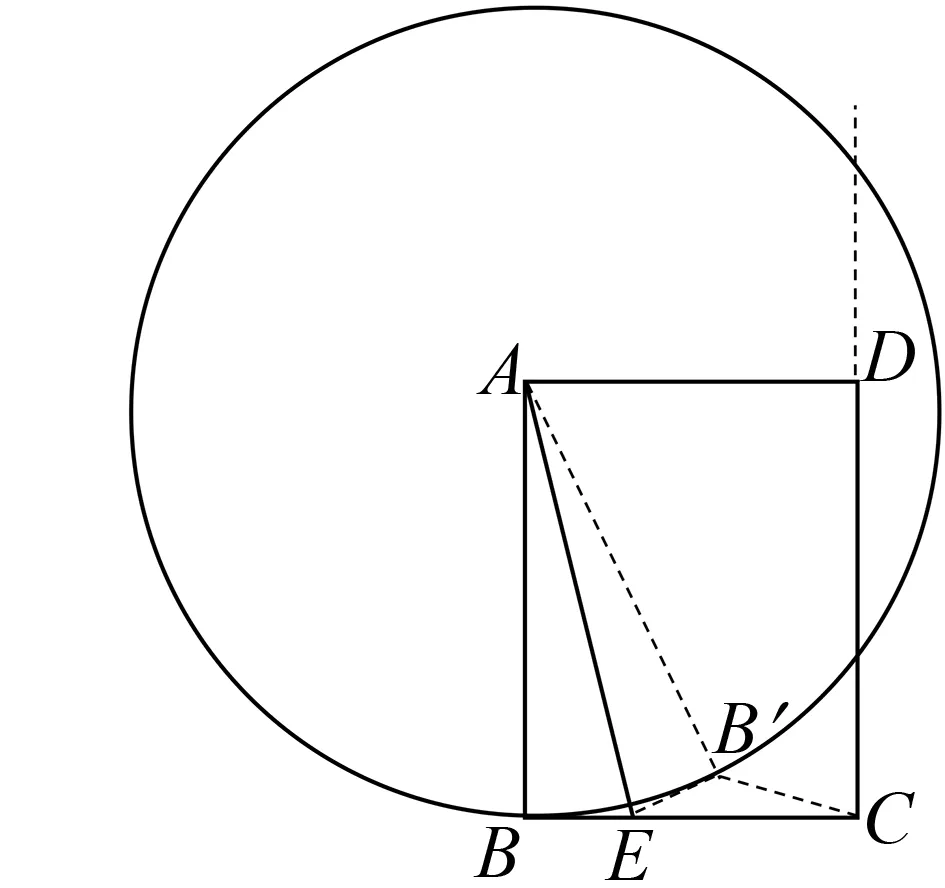
5 结语
