量块混合测量及其测量不确定度分析

2022-01-22武腾腾

电子测试 2021年24期

关键词：量块测量法测量误差

武腾腾

（江西省检验检测认证总院东华计量测试研究院，江西南昌，330000）

0 引言

量块测量是物理试验等研究分析活动中的重要操作环节，其准确性直接影响着研究分析效果。而混合测量法作为目前常用的量块测量方法之一，人们通过明确测量方法的不确定度，能够更合理地应用该项测量方法，提高最终测量结果的可靠性，获得更好的操作效果。

1 量块混合测量法的形成

最早人们使用的量块测量法以直接测量法为主，这种测量方法通常采用干涉操作法来实现，即直接量取量块的长度。但这种操作方法向量块施加的作用力较大，容易影响测量结果，因此，人们又提出了比较测量法，这种测量法的操作方法为，对标准量块、被测量块进行机械比较，以得出两者的差值，再用该差值与标准量块尺寸进行计算，得出被测量块的尺寸，实现量块测量。在此过程中，测量用的主要设施为位移传感器，此类传感器包括接触式干涉仪、光学计等多种类型，且普遍在精度、灵敏度上存在明显的优势，但其量程较小，难以实现对长度差较大量块的测量。基于此，人们开始不断优化传感器，最终制造出了量程更大、分辨率更高的激光干涉仪器，以及位移计等比较测量用设施，这使得比较测量法的应用范围扩展到了长度差几十毫米的量块测量。在大长度差条件下应用的比较测量法，由于长度差较大，所以在具体操作上，又与常规的比较测量法存在较大的差异，因此，人们将大长度差条件下的比较测量法另外命名为混合测量法，由此形成了量块的混合测量法[1]。

2 不确定度评定的特点

不确定度可以被阐释为，对被测量真值所在量值范畴的评定，通常用U来代表。具体来说，其代表了因为误差造成的测量结果不确定的程度。一般来说，不确定度可以表示为误差分布情况，其中，测量误差包括未定系统误差、随机误差两种误差，因此，总体上来说，也可以将其理解为某种误差限值，且该限值具有概率性的特点。

3 不确定度分析方法

3.1 试验方法

根据上述论述，混合测量形成于比较测量，且从本质上来看，两种测量法的基础测量机理均为机械比较测量，因此，可以按照比较测量的方式，进行不确定度的分析。在此过程中，研究者拟结合各类相关理论、推论，运用数学方法，建立一个不确定度测量模型，然后通过测量试验，得出模型计算所需的参数，再将参数代入模型求解，最终得出混合测量法的不确定度，实现不确定度分析。其中，在模型建设中，由于研究者是基于比较测量法建立的模型，但混合法的操作较为复杂，使得比较测量法中可以被忽略的影响因素，因此，前期基于比较测量法所建立的模型并不完整，需要额外确立出混合法中不能忽略的因素，以得出更加完善的混合测量法不确定度测量模型，由此来保证此次分析结果的准确性。

3.2 不确定度测量模型建立

在模型建立中，比较测量不确定度测量模型为，Δl = l - ls=r，其中，l为测量结果、ls为被测真值、r为读数、△l为不确定度。由于测量时的环境温度为20℃，因此，需加入温度修正，将误差进行剔除。为此，将修正公式带入上述模型，可以得到剔除温度粗误差的测量模型为，，其中，t为量块温度、α为膨胀系数、l为环境温度下凌快的中心长度、r为读数，将此公式进行整理，能够得到被测量块长度l为，但为了使各个影响量能够更简单地被分离出来，需要将该公式进行转换得出，

由于在上述公式模型中，存在r远远小于l、α（t-20）远远小于1，因此，可以得出基于此，可将模型简化为，l = ls+ lsαs( ts- 2 0 ) + r - lsα (t -20)。此后，为了使后续的模型运算更加便捷，可以设 Δα = α -αs、Δt = t -ts，同时，考虑到实际测量的长度值，为量块中心长度值，因此需要将中心偏离误差加入到模型中，并将标准量块、被测量块的偏离误差，设为在此过程中，除上述提出的影响因素以外，其他的影响因素基本不会干扰到比较测量的最终值，所以根据上述模型，可以将不确定度测量模型设置为，但事实上，在混合测量中，由于长度差较大，通常无法满足条件r远远小于l，而且rα（t-20）也无法约等于零。为此，设被测真值ls＜测量结果l，那么则可将温度修正后的公式列为，然后将该公式带入到上述不确定度测量模型中，可以得到，

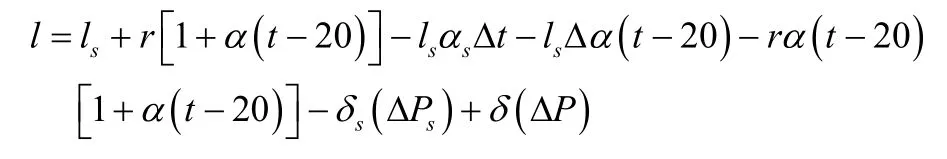
该模型，即为混合测量不确定度测量模型。

3.3 温度因素

从总体上来看，模型中未考虑到，且会影响混合测量结果的因素主要有两项，即温度因素，量块长度方向与测量方向的平行偏移因素。其中，在温度因素方面，模型中仅将温度粗误差剔除，并没有考虑到，误差累计的问题。在此过程中，温度越高每μm长度差的误差就会越高，而混合测量的量块长度差较大，导致误差大量积累，对最终结果产生影响，但因为比较测量下，量块长度差较小，所以误差可以小到忽略不计，所以模型中未能予以体现。为此，研究者在混合测量试验之前，对量块进行了温度平衡试验，计算出相应的误差值，再将误差值确立为不确定度测量模型的条件，健全该测量模型，提高分析结果的可靠性。在温度平衡试验中，恒温实验室的环境温度为20±0.2℃，标准量块长度为10mm、被测量块长度为20mm，然后用误差＜0.01℃、分辨率0.001℃的测温仪，对两个量块进行温度测试，并按照常规的步骤操作多次，最终取值得出被测量块之间的温度差＜0.03℃，被测量块与标准量块之间的温度差为0.026℃～0.063℃。

3.4 不平行因素

原则上来说，比较仪器的测量方向需与量块中心线保持平衡状态，也就是量块工作面需要与仪器的测头呈相互垂直的关系。但实际操作总会存在误差，导致量块与测头之间的垂直度仅能被控制在10以内，因此，量块长度与测量方向并不能达到完全平行的状态。在此背景下，若长度差为1μm，那么所产生的误差则为 1*（1-cos10）=0.000004μm，如果实际的长度差达到1mm，那么就会产生0.004μm的误差，10mm时误差则能达到0.4μm，最终对测量结果产生严重的影响。现阶段，混合测量所用的比较仪器可以被分为两种类型，即上下双测头型、上面单头测量型。如果使用上面单头测量型的仪器，那么就会因为该测量仪器的中筋较高，而造成量块的倾斜，使测量误差增大。一般来说，假设中筋高度为0.04～0.06μm，中筋距离10mm，那么量块的倾斜度就可能会达到1.2”。而比较测量法下，量块长度差较小，并不会形成较大的误差，但混合测量法的量块间长度差可达几十毫米，因此，混合测量法中不能将此影响因素忽略。为此，在测量中，需按照公式1μm*（1-cosA），得出每μm长度差所对应的误差值，然后将误差值作为模型的运算条件，由此得出更加准确的不确定度分析结果[2]。

4 结果与分析

4.1 试验结果

经过上述测量后，得出结果如表1所示。

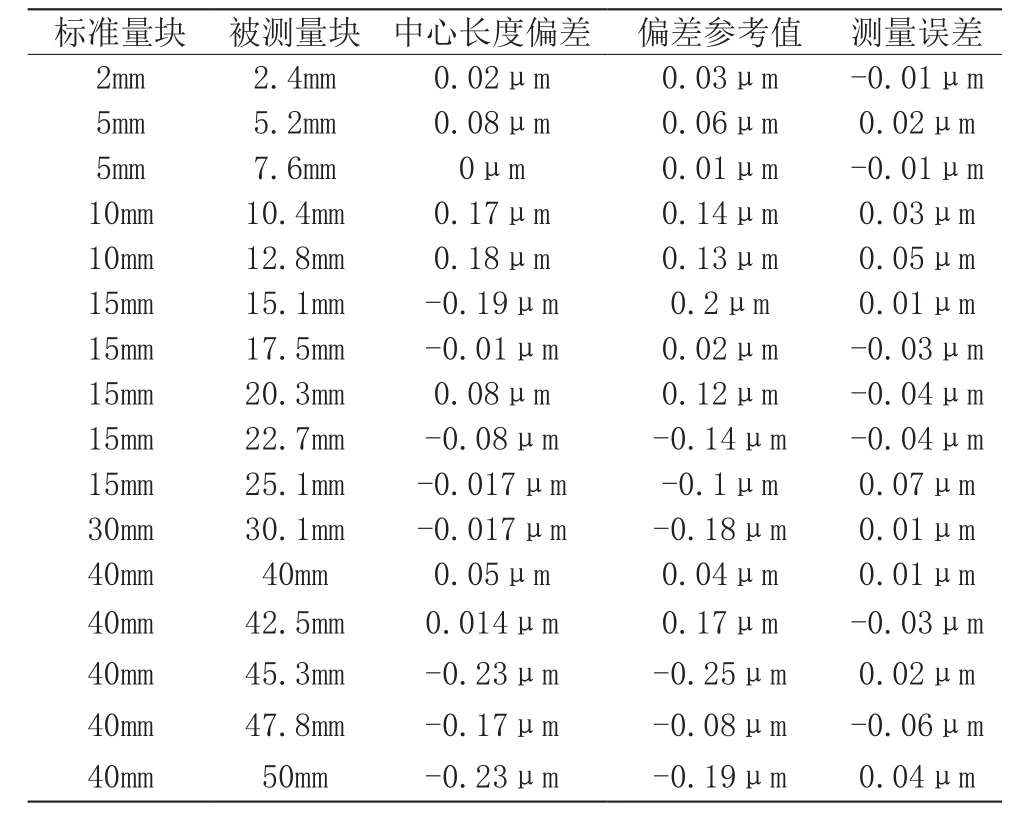
表1 混合测量试验结果表

4.2 结果分析

根据上述结果可以看出，量块长度差小于等于0.5mm时，按顺序来看，测量误差值分别为，-0.01μm、0.02μm、0.03μm、0.01μm、-0.03μm、0.01μm，由此可见，当长度差值≤0.5mm时，测量误差可被控制在±0.03μm以内。但当长度差＞0.5mm之后，误差则会达到-0.06μm，基本很难被控制在0.03μm以内。在此过程中，观察长度差＞0.5mm条件下，测量误差值通常会超过±0.03μm，不过也有误差仅为-0.01μm的情况，而查看此误差结果对应的中心长度偏差可以发现，由于该长度偏差值为0，所以此部分偏差的消除，在很大程度上减少了测量误差，但在常规情况下，这种效果很难达成，由此说明，在长度偏差存在的情况下，若长度差＞0.5mm，则测量误差大于±0.03μm，且可能会达到-0.06μm。结合上述论述，大误差的形成主要源于操作过程中误差的积累。在混合测量中，操作步骤较多，而每步操作均会增加单位长度的误差值，同时，应用混合法进行测量的量块长度差较大，导致误差大量积累，尤其是在长度差超过0.5mm之后，误差值会迅速增加，对测量结果产生较大的影响。根据文章开头的论述，不确定度可以表示为误差的分布情况，由此即可分析出不确定度分析结果为，若中心长度偏差存在，当长度差值≤0.5mm时，误差在±0.03μm，当长度差值＞0.5mm时，误差则会超过0.03μm。

5 讨论

基于上述结果分析可知，混合测量法的不确定度分析步骤更加复杂，且该方法的不确定度也更大。但在实际应用中，如果能够将被测量块与标准量块之间的差值控制在0.5mm以内，那么应用此方法依然能够得到较为准确的测量结果，但若长度差超过了10mm，则可能出现测量误差成倍增长的情况，因此，在量块测量中，如果运用此方法，且长度差较大，那么就应当在误差修正上，注意对不确定度进行重点的考量，以缓解测量误差的问题。