ISOS-DAB系统电压上翘控制策略研究
2022-01-22陈良胜林文强潘尚智宫金武查晓明
陈良胜,林文强,潘尚智,宫金武,查晓明
(武汉大学 电气与自动化学院,武汉 430072)
近年来,随着分布式能源的逐步发展,直流电网得到越来越多的研究[1],下一代高压直流电网技术将成为未来电网发展的重要方向[2-3].目前有关直流电网的研究集中在关键设备研发、电网架构、调度与控制、运行与保护等方面[4-6].其中,直流变压器作为直流电网中能量汇集与分配的枢纽,受到广泛关注.同时伴随着电力电子技术的快速发展,国内外众多学者围绕直流变压器的拓扑和控制开展了全面研究.
目前直流变压器的中压侧电压通常高达10 kV等级,而功率半导体器件即使经过若干次更新换代,电压等级和容量大幅提升,但其发展跟电网的要求仍有较大差距,因此面对电力系统高压大功率应用需求,更需要对电路拓扑展开研究[7].输入串联输出串联(Input Series Output Series, ISOS)拓扑,由于其模块化程度高,具有较高的可靠性和冗余性,并能减少制造时间和成本[8-9]可有效解决耐高压的问题.双有源桥(Dual Active Bridge,DAB)DC-DC变换器结构简单,能够实现电气隔离和能量双向流动[10],同时,它能充分利用变压器的漏感能量,易实现软开关,降低开关损耗,是ISOS拓扑理想的基本模块.
然而,各DAB变换器的变压器变比、漏感等参数不可能完全一致,易导致模块间功率不均衡现象,因此如何确保功率均衡对于正常运行至关重要.对于ISOS拓扑,即要保证模块间的输入均压(Input Voltage Sharing, IVS)和输出均压(Output Voltage Sharing, OVS).文献[11-13]采用共同占空比控制,解决了输入串联输出并联(Input Series Output Parallel, ISOP)的功率均分问题.但是文献[14]研究表明针对于一般的ISOS拓扑,即使模块间参数差异很小,使用共同占空比控制方案也无法稳定.文献[15]采用包括系统输出电压外环、输入电压前馈环和电流内环的三环控制策略,以实现各个模块间的功率均衡,直接实现IVS,自动实现OVS,但是检测信号过多,控制复杂.文献[16]通过交换两模块的占空比可以实现两模块结构下的IVS和OVS.文献[17]将其拓展到更多模块,然而此时每个模块需要采集所有模块输出电压信息,极大地增加了控制的复杂程度.文献[18]提出了一种主从控制方案,即使模块数量增加,它仍然具有简单的结构,适用于多模块系统,但此方法严格依赖于主模块的稳定性.文献[11-18]的控制策略都要求所有模块共用一个中央控制器或者严格依赖于主模块的工作状态,导致系统的冗余性和可靠性较低.下垂控制方案可以通过无互联通信实现模块间均流的效果,文献[19-20]基于下垂控制,提出了一种ISOS拓扑的输出电压上翘特性的分布式均压控制策略,所有模块主电路和控制电路相同,消除了中央控制器和主从控制器的区分,从而保证了ISOS的模块化设计和较高的系统可靠性。
基于DAB的ISOS拓扑在输入输出侧均能承受较高的电压,在直流电网中有十分适配的应用场景,具有很重要的研究价值.针对ISOS拓扑的众多均压控制策略,输出电压上翘控制能够保证很好的系统可靠性,有利于系统安全运行.然而目前基于ISOS-DAB系统的上翘控制策略研究较少,并且缺乏完整的可行性理论分析过程,因而本文作者将基于此展开研究.首先,进行小信号建模,给出完备的稳定性分析过程;然后,结合PSIM软件进行仿真分析;最后,设计样机进行实验验证,综合分析上翘控制策略在ISOS-DAB系统中的适用性与稳定性.
1 DAB工作原理和小信号建模
1.1 DAB工作原理
典型DAB变换器如图1所示,其中Uin、Uo分别为输入、输出电压,Uab为AB之间电压,Ucd为CD之间电压,I1和I2分别表示输入、输出电流,Lr为外加电感与变压器漏感之和,ILr为原边电感电流,ULr为电感电压,Cd、Cf分别为输入、输出侧电容,变压器变比为n,Q1~Q8为开关管.

图1 双有源全桥 DC-DC 变换器
DAB的等效电路如图2所示,电感Lr是整个变换器能量传递的载体.
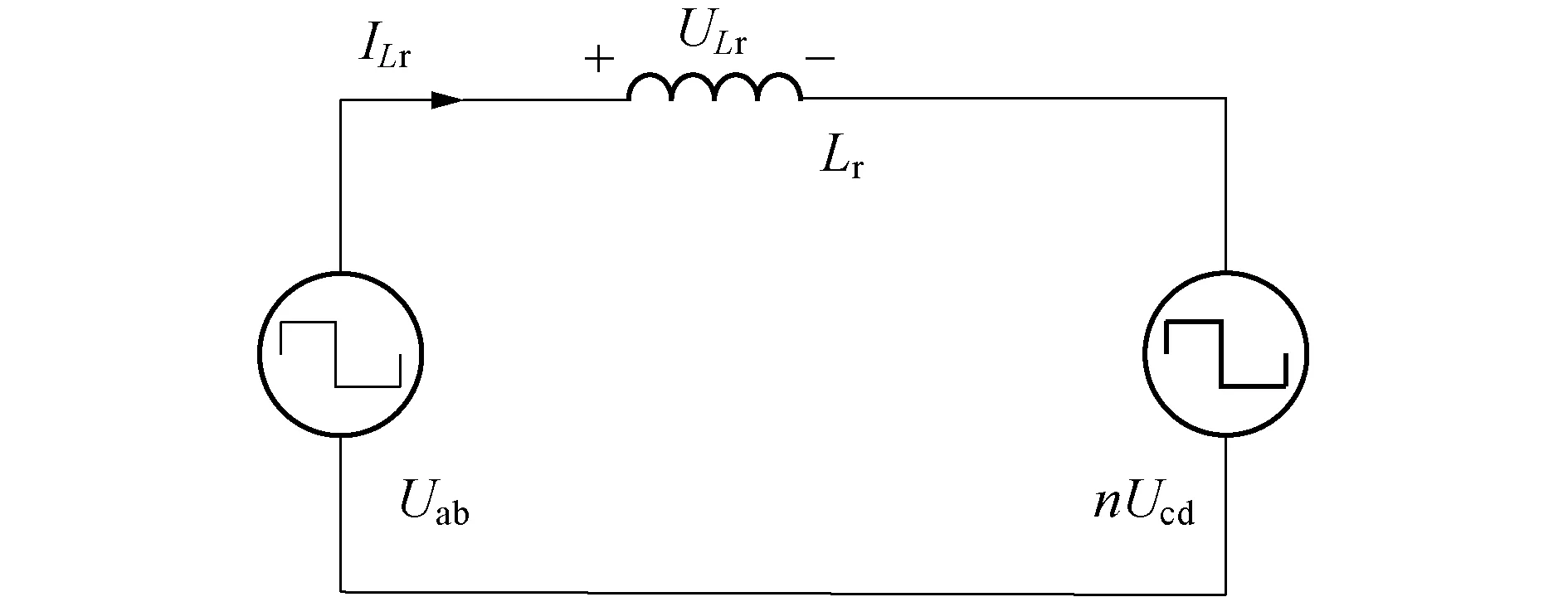
图2 DAB的等效电路
典型DAB控制方法主要有3种:变频控制、占空比控制和移相控制.其中移相控制通过调节电感Lr两端电压移相角,控制功率传输的大小和方向,实现软开关容易、动态响应快,因而更为常用.随着控制自由度数量的变化,移相控制分为单移相、双移相、三移相等[21-22].单移相控制(Single Phase Shift, SPS)简单,在非轻载、输入输出电压匹配的工况下,DAB传输效率较高[23],本文侧重于解决各模块间的均压问题,故选择SPS作为DAB变换器的控制方式.SPS只有一个控制自由度,即原副边H桥之间移相角与180°的比值,称作移相比D.在不考虑死区时间的情况下,各桥臂上下两个开关管互补导通,所有导通信号占空比均为50%.SPS控制下的DAB运行波形图如图3所示,展示了t0~t11时间段内的开关管工作过程,以及相关电压电流波形,Ts为开关周期.

图3 单移相调制下DAB运行波形示意图
1.2 DAB小信号建模
为了验证系统稳定性,首先对DAB变换器进行小信号建模.
SPS控制下DAB的传输功率表达式为
(1)
式中:P表示每个模块的传输功率;fs表示开关频率.由式(1)推导得到输入和输出电流的表达式为
(2)
为了得到DAB小信号模型,可以用一个稳态工况下的直流量和一个小信号扰动量迭加表示DAB中的所有变量,可以得到
(3)

综合式(2)、式(3)可得
(4)
忽略直流项和次数大于2的高阶小项,即可得到DAB的输入、输出电流的小信号表达式
(5)
(6)
式中:Gi1d为输入电流对移相角的偏导数;Gi1uo为输入电流对输出电压的偏导数;Gi2d为输出电流对移相角的偏导数;Gi2uin为输出电流对输入电压的偏导数.
由此可得DAB的小信号模型如图4所示.
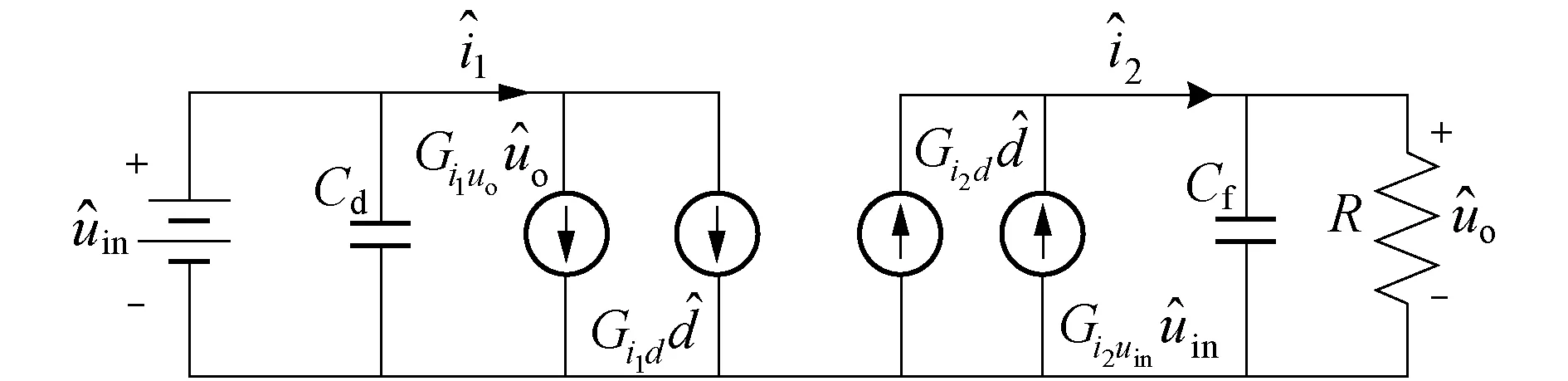
图4 DAB的小信号模型
至此已经建立了单个DAB变换器的小信号模型,但要获得ISOS-DAB系统的闭环阻抗方程,还需要引入控制电路的部分.
2 上翘控制策略原理和稳定性分析
本文将文献[19-20]的输出电压上翘控制策略引入ISOS-DAB系统,建立该系统的完整小信号模型,通过根轨迹法验证其在基于ISOS-DAB系统中的适用性与稳定性.
2.1 输出电压上翘控制
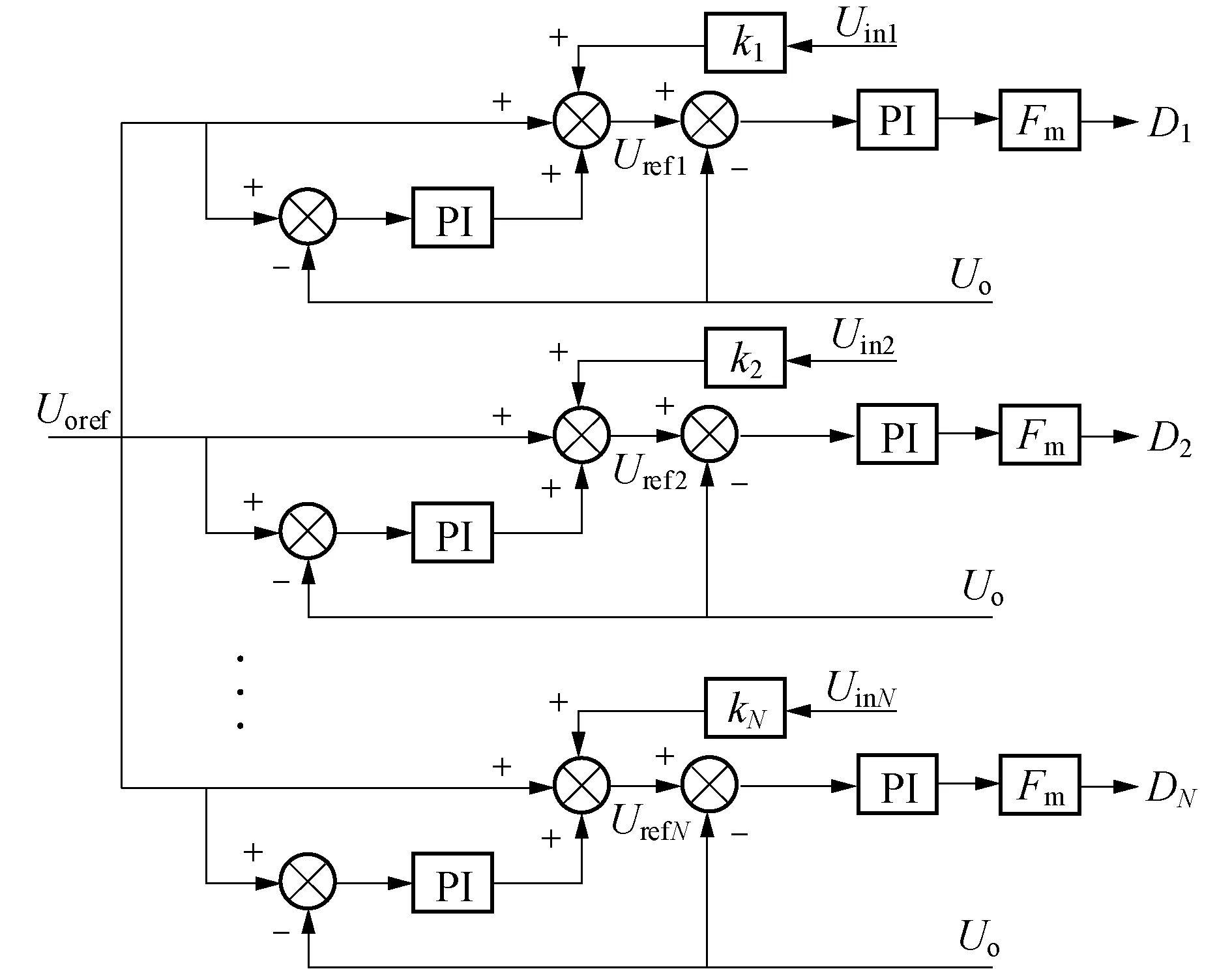
上翘控制策略基本原理就是将输入电压以一定的比例叠加到系统输出电压参考值上,每个模块均采用相同的控制方式,且只需要采集系统输出电压和自身输入电压,模块间不需要进行控制上的联系,如图5所示.

图5 单个模块的上翘控制策略
图5中,Urefj是实际的输出电压参考值;Uoref是给定的电压参考值;kj是上翘系数;Uinj是单个模块的输入电压;j取1~N,N是模块总数;PI表示比例积分(Proportional Integral,PI)调节器;Fm表示PWM波发生器增益.
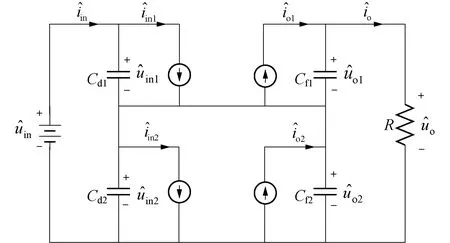
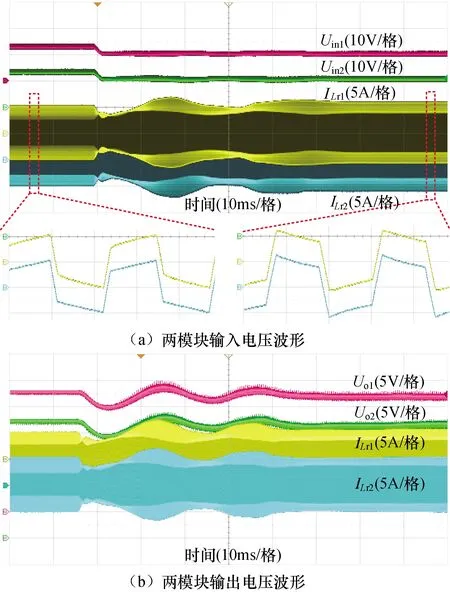
为了便于分析,以如图6所示的两模块ISOS拓扑为例进行原理说明,假设两模块具有完全一致的如图7所示的输出电压上翘特性.图6中,由于串联关系,Iin、Iin1和Iin2均表示总输入电流;Io、Io1和Io2均表示总输出电流;Icin1和Ico1分别表示模块1的输入、输出电流;Icin2和Ico2分别表示模块2的输入、输出电流;ICd1和ICd2分别表示两输入滤波电容的电流;ICf1和ICf2分别表示两输出滤波电容的电流.在稳态下,这两个模块实现输入均压,并同时在O点工作.假设输入滤波电容上的电压发生扰动,Uin1减小,Uin2增加,即Uin1 图6 输入串联输出串联结构 图7 两模块输出电压上翘调整特性 图8 ISOS-DAB系统小信号模型 为了便于分析,假设两个DAB模块的上翘系数、变压器变比、总电感值和输出滤波电容值相同,即k1=k2=k,n1=n2=n,Lr1=Lr2=Lr,Cf1=Cf2=Cf,输入滤波电容Cd1与Cd2不相等,且稳态时满足以下条件,D1=D2=D,Uin1=Uin2=Uin/2,Uo1=Uo2=Uo/2,其中D1和D2为两模块稳态工况下的移相比,Uo1和Uo2分别为两模块稳态时的输出电压. 由图8可推导出 (7) (8) (9) (10) (11) 式中:Gv为PI调节器. 由式(7)~式(11)可以推导出每个DAB的闭环输入阻抗Zeq为 (12) 对于ISOS-DAB系统,每个DAB模块可由其输入均压电容和输入阻抗并联代替,再将等效子模块电路进行串联连接,即可得到图9所示的等效模型. 图9 ISOS等效模型 PI调节器的一般形式为Gv=kp+ki/s,kp、ki分别比例、积分系数,由此得到ISOS-DAB系统输入电压扰动的传递函数为 (13) 提取式(13)分母,即可得到特征根方程 D(s)=a3s3+a2s2+a1s1+a0 (14) (15) 系统相关参数见表1. 表1 系统参数 将表1中相关参数代入式(14)可得特征根方程为 D(s)=7.3728·10-6s3+0.0187kps2+ (0.0187ki+0.9295kp+0.0181)s+0.9295ki (16) 式(16)中只剩PI控制器的参数待确定,现选取合适的kp与ki值,对系统进行根轨迹分析.当kp=0.1,ki在0.1到100内变化时,根轨迹如图10(a)所示.当ki=10,kp在0.001到1之间变化时,根轨迹如图10(b)所示. (a)固定kp,改变ki 可以看出两种情况下,随着PI参数的变化,系统的特征根始终分布在左半平面,说明当选取合适的PI参数时,系统能够达到稳定.因此通过小信号建模分析给出了完备的证明过程,充分验证了上翘控制策略在ISOS-DAB系统中的稳定性. 依据图11建立了ISOS-DAB系统的PSIM仿真模型.已知DAB模块的参数不一致会导致系统功率不均衡,即无法实现IVS和OVS.由于电感是DAB模块能量传输的载体,因此设置两DAB模块的总电感值分别为24 μH和26 μH,其他参数与表1一致,以此探究上翘控制能否实现均压效果. 图11 两DAB构成的ISOS主电路图 ISOS-DAB系统采用如图12所示的上翘控制策略,可知各控制器相互独立,均只采集系统输出电压信号和模块自身输入电压信号,基于上翘控制的仿真结果如图13所示. 图12 ISOS的上翘控制策略 图13 校正前的仿真结果 由图13可知,模块输入侧与输出侧实现了很好的均压效果,且响应较为迅速,但是由于输出电压参考信号叠加了一定比例的模块输入电压,导致系统实际输出电压高于参考值,与理论分析一致.因此可以加入一个校正环节,将系统输出电压调节回参考值,如图14所示,新添加的PI调节器实时监控输出电压与参考值,可以有效补偿因为输出电压上翘特性带来的电压偏移,添加校正环节之后的仿真结果如图15所示. 图14 添加校正环节后的上翘控制策略 图15 校正后的仿真结果 由图15可知,在添加了校正环节之后,系统输出电压被拉回至参考值,电压偏移问题得到解决,而两模块的输入输出侧均实现了很好的均压效果,从而说明仿真也验证了上翘控制策略在ISOS-DAB系统中的适用性与稳定性.仿真中使用的PI参数分布在图10的根轨迹图中,验证了针对ISOS-DAB系统小信号建模的准确性,也证实了仿真结果与理论分析的一致性与正确性. 为了进一步验证上翘控制策略在ISOS-DAB系统中的有效性,设计了由两个DAB模块构成的组合系统样机,总输入电压范围为18 V~30 V,系统输出电压额定值为40 V,其他实验参数参见表2,基于样机进行了不同工况下的实验验证. 表2 实验参数 根据不同输入电压下实测的输出电压值,绘制出两模块的输出电压上翘特性曲线,结果如图16所示.由图16(a)可知,未添加校正环节时,当总输入电压从18 V变化到30 V,系统输出电压由44.7 V增加至47.5 V,结果符合上翘特性,且全过程两模块满足了均压要求.由图16(b)可知,添加校正环节之后,当总输入电压从18 V变化到30 V,系统输出电压由40.1 V增加至40.8 V,基本消除了由于上翘特性带来的电压偏移,且全过程两模块仍能满足均压要求. 图16 输出电压上翘特性曲线 为了进一步验证上翘控制策略的稳定性,测试输入电压突变和负载突变下的工况,实验结果如图17和图18所示.图17所示的为两DAB模块输入输出电压波形以及各自的电感电流波形,可知当总输入电压由26 V突变至21 V时,两个DAB模块的输入输出电压始终达到均衡,系统输出电压额定值为40 V,而两模块输出电压之和,即系统输出电压在变化前后均高于40 V,且随着输入电压的减少而下降,符合输出电压上翘特性,电感电流波形也符合SPS调制下的特征.由图18可知,当负载由重载切向轻载时,电感电流峰值减小,此时两模块输入电压几乎不受影响,且保持相等,而输出电压经过短暂的调节之后,依旧能维持均衡状态. 图17 输入电压突变实验波形 图18 负载突变实验波形 1)研究了基于DAB模块的ISOS(ISOS-DAB)系统的模块间功率均衡问题,在ISOS-DAB系统中引入了输出电压上翘控制策略,对该系统进行了详细的小信号建模,模型构建准确,理论分析证明了上翘控制在ISOS-DAB系统中的稳定性. 2)在小信号建模基础上开展了仿真和实验验证,仿真和实验结果均证明了上翘控制在ISOS-DAB系统中的适用性和稳定性,在无互联通信的基础上仍能保证IVS和OVS的实现,提高了系统的模块化程度. 3)基于此结果,今后将继续研究,扩展至其他的模块组合方式上,期望实现即插即用的高度模块化功能.

2.2 ISOS-DAB系统小信号建模分析





3 ISOS-DAB系统仿真




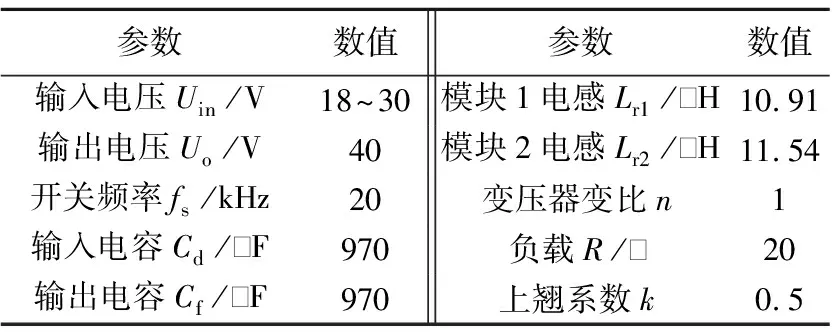
4 实验验证


5 结论
