相量法在正弦稳态电路中的应用研究

姬芳芳，崔乃忠

物理科学与技术

相量法在正弦稳态电路中的应用研究

姬芳芳，崔乃忠

（唐山师范学院 物理科学与技术学院，河北 唐山 063000）

系统地阐述了相量法在正弦稳态电路中的应用，结合实例说明了分析问题的关键和解题技巧。最后指出，相量法并不是万能的，对于求解较为复杂的正弦稳态电路，要具体问题具体分析。

相量法；正弦稳态电路；正弦量；相量图；电路分析方法

相量法是在数学理论和电路理论的基础上建立起来的一种系统方法，对分析正弦稳态电路实用、有效。该方法用相量的形式表示正弦量的振幅和相位，将表示不同物理意义的正弦量由时域引入到复数域，在复数域建立电路相量模型，实现相量运算，从而简化时域中正弦稳态电路的复杂计算过程。相量概念的引入把直流电路的分析方法推广到了交流电路，在直流电路中基尔霍夫定律、网孔电流法、回路电流法、结点电压法等电路分析方法在交流电路中借助相量模式仍然适用[1-2]。

1 正弦量的复数表示方法

在复数域，任一复数可以有四种表达式：

图1 复数表示法之间的关系

上述四种表达式是等价的，它们之间的关系见图1。其中

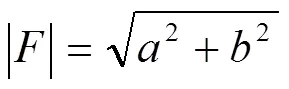
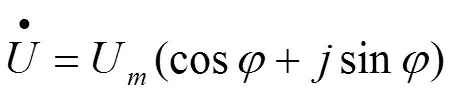
为了和一般复数相区别，把表示正弦量的复数称为相量[3-4]。

在正弦稳态电路中，激励与响应均为同频率的正弦量，激励的频率通常为已知条件，所以确定一个正弦量只需求得其振幅和初相位。

2 电阻电感电容元件在交流电路中的相量形式

图2 电阻、电感、电容元件相量图

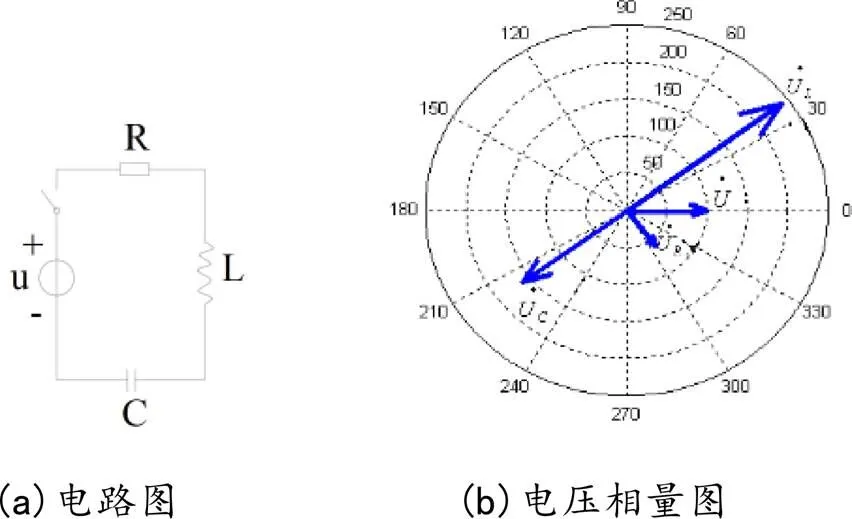
图3 例1分析用图

3 用相量图法求解正弦稳态电路

应用相量图分析正弦稳态电路，可以通过确定与参考相量的对应关系把各元件的电压或电流相量放在同一相量图中，从而直观地展示各相量关系。借助相量图并结合某些特殊平面几何图形的特性，挖掘潜在的未知参数，寻找待求相量的幅值和初相位，最终完成题目求解。

绘制相量图的关键是选择参考相量。参考相量选择的准确与否直接影响相量图的直观性以及求解的难易程度。一般来说，依据电路连接形式不同，参考相量的选择也各不相同。对于串联电路，因流经各元件的电流是相同的，选择电流作为参考相量比较方便；对于并联电路，一般选择支路电压为参考相量。在混联电路中，情况较为复杂，参考相量的选择没有固定的模式，多数情况下会从局部相量入手。若局部电路有并联部分，则会以并联部分的电压相量为参考相量，再依据支路电路中电压与各支路电流的相位关系画出相应相量，最后依次做出其余部分的电压、电流相量，直至完成整个相量图。

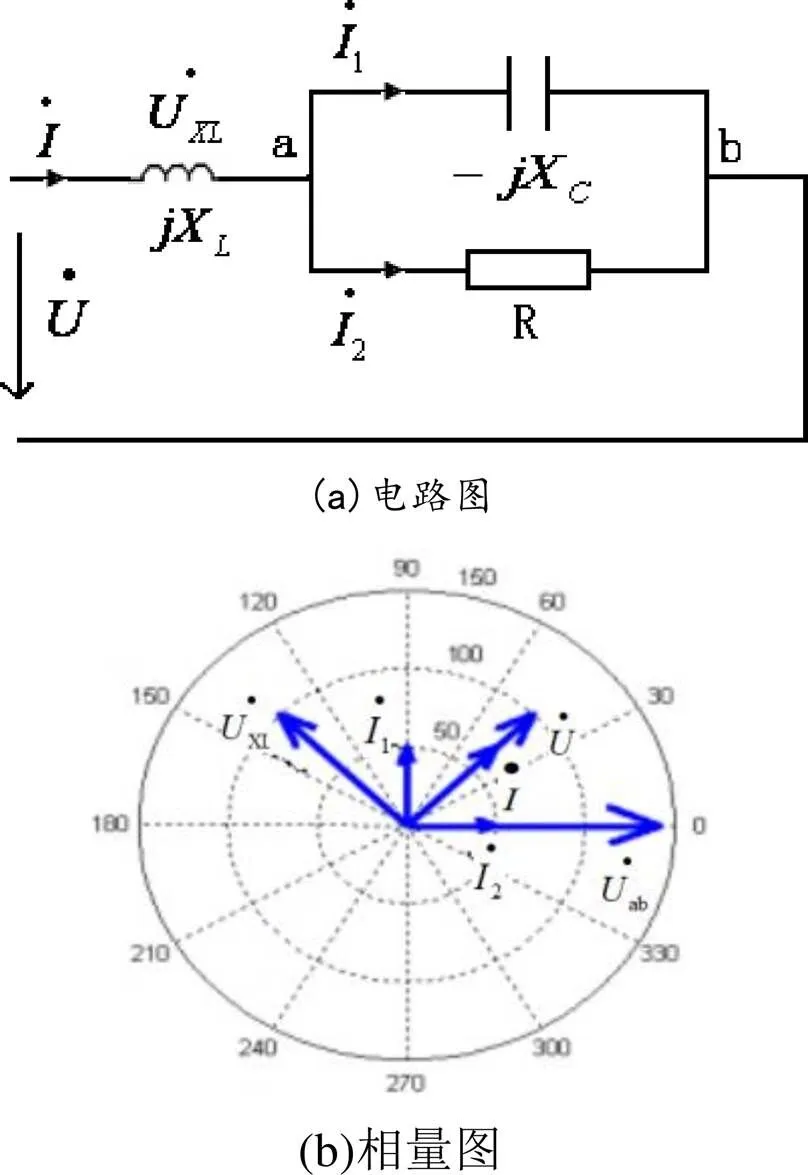
图4 例2分析用图

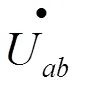
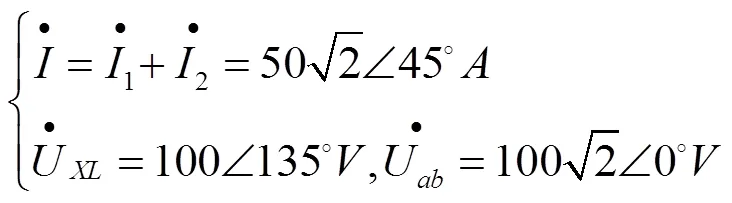
4 电路分析方法在正弦稳态电路中的应用

在求解较为复杂电路时，可能不易得到完整的相量图，直接应用电路定理求解，往往更为简便，而且在正弦稳态电路中，直流电路的分析方法和电路定理仍是适用的。将电路中所有的电路元件以及它们对应的电压、电流用相应的相量式代替，然后依据电路定理即可建立与原电路对应的相量模型，即相量形式表示的代数方程。

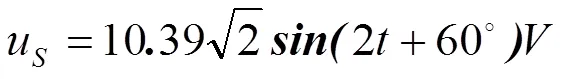
电流源为

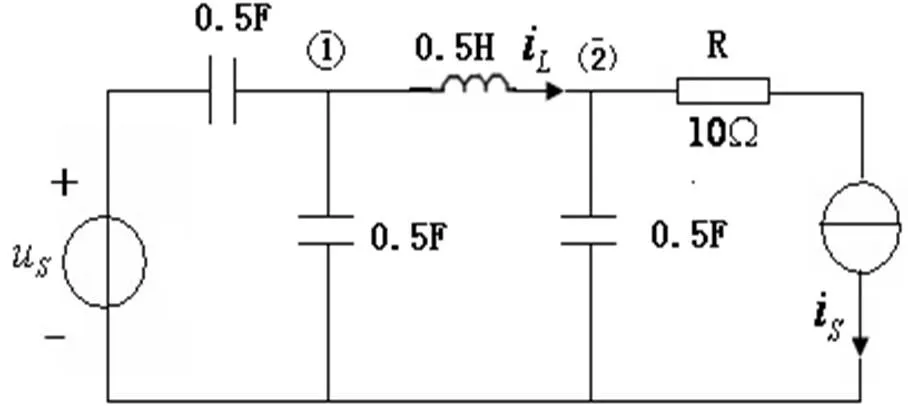
图5 例3电路图

分析 首先需要建立各元件对应的相量模型。用相量式表示各参量为：

之后运用相量形式的电路定理解题即可。

本题有多种解法，现以结点电压法为例。对1、2两个结点列方程如下：

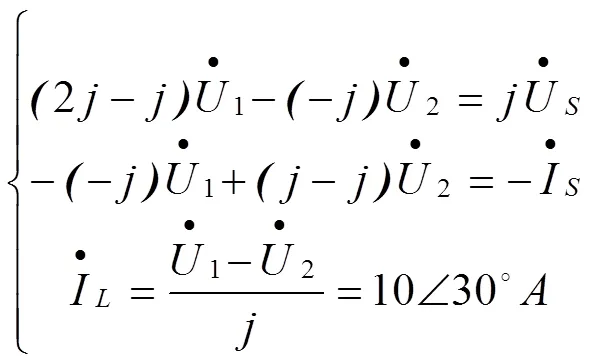
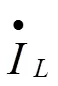
5 结论

用相量表征正弦量，把参数从时域引入到复数域，通过画相量图，确定各个相量之间的关系，利用几何图形特性，求解未知量。这样的解题过程具有显著的直观特性，在支路较少电路中可以避免繁琐的运算，并且能够加深学生对正弦交流电路的概念和规律的理解。对于较为复杂的电路，可借助电路定理、电路的分析方法，以相量形式描述电路定理，用复数表示求解结果。总之，相量法将直流电路和交流电路的分析过程紧密结合，为分析正弦稳态电路提供了一条便捷途径。

[1] 崔乃忠.电路教学中含受控源电路的分析与探讨[J].大学物理,2008,27(2):33-35.

[2] 姬芳芳.由一道“一题多解”的电路分析题想到的[J].唐山师范学院学报,2019,41(6):43-46.

[3] 邱关源.电路[M].第5版.北京:高等教育出版社,2006:202- 219.

[4] Charles K, Matthew N O Sadiku.电路基础[M].段哲民,周巍,李宏,译.北京:机械工业出版社,2014:278-300.

Application of Phasor Method in Sine Steady-State Circuit

JI Fang-fang, CUI Nai-zhong

(School of Physical Science and Technology, Tangshan Normal University, Tangshan 063000, China)

The application of phasor method in sinusoidal steady-state circuit was systematically expounded in this paper. The key of analyzing problems and solving skills in examples were illustrated. The phasor method was not omnipotent, and the solution of the more complex sinusoidal steady-state circuit should base on the specific situation

phasor analysis; Sine Circuit; Sinusoidal quantity; Phasor diagram; Circuit analysis method

G424.1

A

1009-9115(2021)06-0029-03

10.3969/j.issn.1009-9115.2021.06.008

唐山师范学院教改项目（2020JG014）

2021-06-17

2021-09-09

姬芳芳（1984-），女，河南焦作人，硕士，副教授，研究方向为机械工程。

（责任编辑、校对：侯 宇）