基于反向学习的布谷鸟算法优化搜索仿真

胡安明，李 伟

(1.广州理工学院计算机科学与工程学院，广东 广州 510540；2.集美大学理学院，福建 厦门 361021)

1 引言

布谷鸟搜索(Cuckoo Search，CS)算法是依据布谷鸟在其他鸟巢中的育雏行为与其它鸟类的Levy flight行为，提出的搜索算法。布谷鸟算法由于其简单高效的特点，自提出之日起，就在工程优化和函数优化等方面广泛应用。但是也存在相应的弊端，在处理一些复杂的问题时，布谷鸟算法无法展现出高效的搜索能力和收敛速度，以至于后期无法满足最优解的精度需求，因此还需对其进行深入的优化和研究。

黄闽茗等人[1]针对布谷鸟算法搜索性能不足和收敛速度较慢等问题提出了优化方案。对更新后的解进行逐维反向学习，将影响计算的干扰因素控制在最低；利用精英反向学习提高算法和动态适应的缩放因子，对当前解的信息做进一步控制，以此提高算法的收敛速度和搜索性能。虽然该方法提升了布谷鸟算法的搜索能力，但存在搜索繁琐的问题，不适用于大范围搜索；张燕等人[2]为了提高布谷鸟算法求解多维函数的能力，通过局部搜索增强策略增加布谷鸟的种群范围，增加可选择性，避免陷入局部最优；然后利用自适应发现概率使得局部求精和全局寻优之间获得平衡；最后加入反向学习扰动机制增强算法找到最优解的概率。该方法提高了布谷鸟算法的寻优性能，但是搜索性能有待进一步提升。

基于以上方法的启发和出现的问题，本文在反向学习的基础上提出了一种布谷鸟算法优化搜索方法。通过确定布谷鸟种群中的精英个体，对其求得反向解，丢弃较差解，在较优解中找到最优解作为下一次迭代个体；同时，本文引入了混沌扰动策略，对较优的鸟巢位置进行混沌扰动操作，扩大种群范围，使算法寻优范围更广，搜索能力更强。在仿真中，本文方法提高了处理单峰函数和多峰函数的收敛精度，提升了布谷鸟算法性能。

2 布谷鸟搜索算法实现过程

CS算法的实现是根据布谷鸟找到最佳巢穴的位置[3]映射到种群空间中的解，并根据选择的鸟巢的好坏作为评价算法适应度的标准。为了更形象地展示出布谷鸟的育雏行为，将CS算法控制在三个理想规则之下：

规则一：每只布谷鸟只生产一个蛋，随机放入其它鸟类的巢穴中。

规则二：在布谷鸟繁衍后代的整个过程中，都将最优蛋的鸟巢保留给下一代。

规则三：其它鸟类巢穴被占领的数量[4]是固定的，布谷鸟寄生的蛋被发现后可被破坏或者停止孵化。

根据以上三条理想规则，可将CS算法的实现过程分为四步：

1)初始化设置参数

假设有n个鸟巢，原始位置为Xi=(1，2，…，n)，目标函数为F(x)，发现概率值为Pa，并对最大迭代次数和问题维数进行初始化设置。

2)搜索过程

对所有鸟巢位置计算F(x)，获得所有鸟巢位置的函数值，计算所有鸟巢函数值后，对比所得适应度函数值[5]，找出最优函数值，利用Levy flight的随机步长计算公式如式(1)所示

xt+1，i=xt，i+α0⊗Levy(β)

(1)

式中，xt+1，i表示更新后的鸟巢位置；xt，i表示未更新前的鸟巢位置；α0为步长缩放因子，一般情况下取值0.01；⊗为卷积运算；β为Levy flight的控制因子。

Levy flight的路径选择具有随机性，可用式(2)表示为

(2)

其中，u、υ均表示标准正态随机变量，一般情况下取值1.5。Φ的计算公式如式(3)所示

(3)

3)鸟巢更新选择

计算Pa的值，放弃容易被其它鸟类发现的巢穴，对保留下来的蛋重新计算其位置信息和适应度函数[6]值Ft，选择最优值留下来。更新后蛋所在的鸟巢位置信息如式(4)所示

xt+1，i=xt，i+r(xt，j-xt，k)

(4)

式中，r表示比例因子，为区间(0，1)中的均匀分布随机数；xt，j、xt，k分别为t代中的两个随机解。

4)算法结束

通过上述求解过程，如果得到满足条件的求解精度和最大迭代次数，则停止计算，否则返回步骤2)重新计算。

布谷鸟算法的实现过程如图1所示。

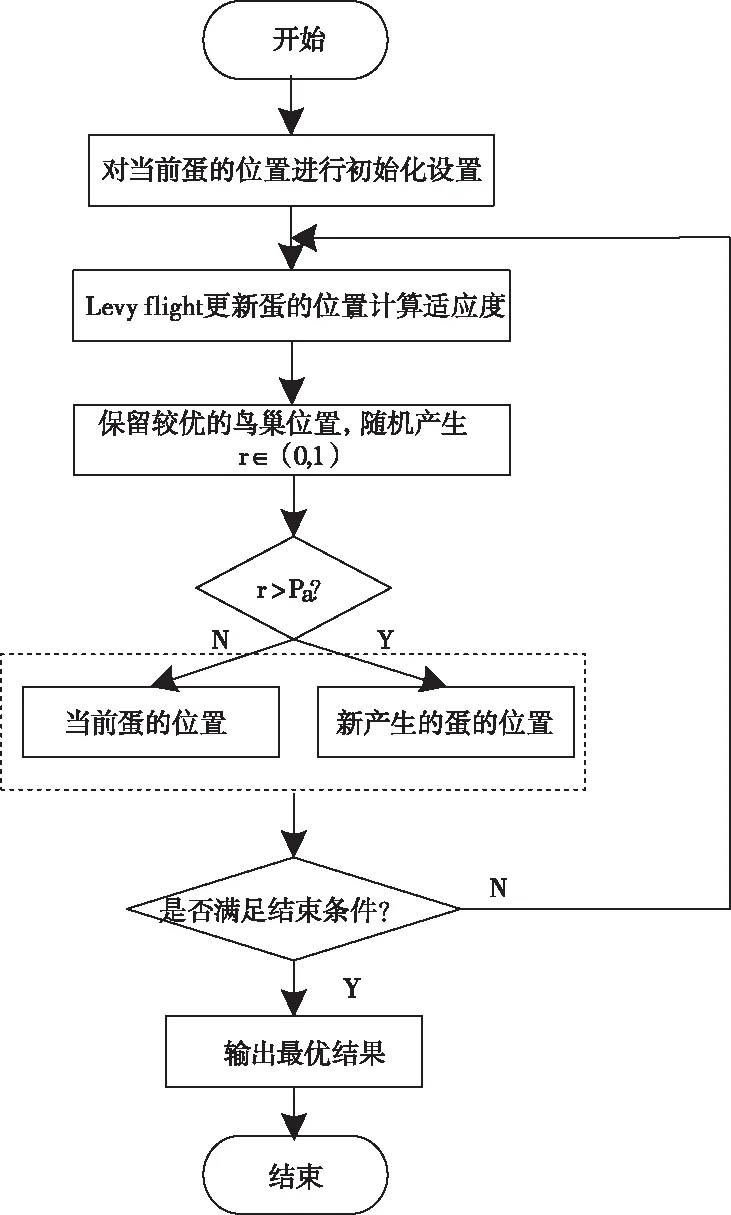
图1 布谷鸟算法实现流程图

3 基于反向学习的布谷鸟算法优化搜索

3.1 加入混沌扰动的CS(CH-CS)

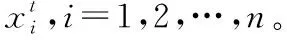
nextbest，d=nextbest，d-1+Rd[2xd(i)-1]

(5)

式中，xd(i)表示当前计算过程中产生的混沌序列，具体过程如下所示

1)随机产生一个D维向量xi=(xi，1，xi，2，…，xi，D)，每个分量取[0，1]区间内的任意数值。

2)优化混沌序列[8]，本文选择kent混沌映射实现优化，算法如式(6)所示

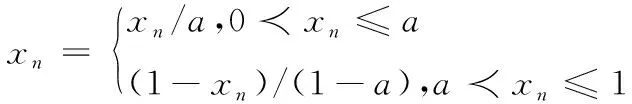
(6)

其中，a=0.4。根据式(6)做迭代计算，再进行第j次迭代后，产生第j次混沌序列：x(j)=x1(j)，x2(j)，…，xD(j)。

确定混沌扰动的区域半径是实现混沌扰动策略的关键步骤。如果区域半径过大，导致对鸟巢位置的确定偏差过大。对于不同的维数值，选取扰动区域半径也有所不同，本文选择逐维变化混沌扰动的方法确定不同的区域半径大小，如式(7)所示

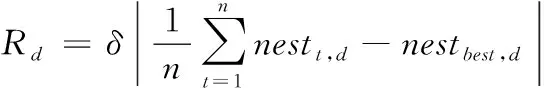
(7)

加入混沌扰动策略后，原始的CS转换为CH-CS，算法流程如下所示：

1)遍历当前所有的布谷鸟群体，确定n个鸟巢的初始化位置信息；

2)对所有鸟巢进行适值fi计算；

3)通过Levy flight得到新的解Ti；

4)对新求得的解Ti进行适值FTi计算；

5)确定候选解Tj的具体数值；

6)对候选解Tj进行适值FTj计算；

7)如果FTi≻FTj，则停止计算；否则返回步骤4)；

8)寻找新的解取代当前候选解；

9)计算布谷鸟的蛋被其它鸟类发现概率值，并丢弃不理想解；

10)计算式(1)得到新的解，取代被丢弃的解；

11)经过多次计算得到最优解，即最佳的鸟巢位置P；

12)利用式(5)对P进行混沌扰动学习，从而得到布谷鸟选取的新鸟巢位置信息P1。测试P和P1中的所有鸟巢，并对比其测试值，表现不好的鸟巢可直接舍弃。对所有鸟巢计算完成后，得到最佳鸟巢位置；

13)结束计算。

3.2 加入反向学习的CH-CS

3.2.1 精英个体的确定

反向学习作为在智能计算领域中热度极高的一种新算法，对于全局寻优展现出了良好的性能。其基本思想为：对于任意给定的可行解[10]，通过反向学习策略得到该可行解的反向解，对比可行解和反向解，筛选出其中表现较优的解，作为下一次迭代个体。反向学习具有强大的包容性，在计算的同时保持了种群的多样性。但同时也出现一定的弊端，在面对数量巨大的种群个体时，如果对所有个体都进行反向解运算，计算量较大且极易降低搜索精度。因此，在运用反向学习算法前，应该确定好精英个体的有效信息，只针对精英个体进行反向解运算，引导搜索结果更靠近最优解，具体过程如下所示。

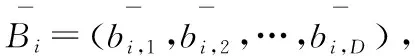
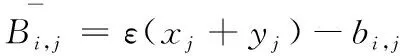
(8)

式(8)中，bi，j∈[xj，yj]，[xj，yj]表示搜索范围的动态边界信息，ε∈[0，1]为一般化系数。

3.2.2 算法优化

对于布谷鸟算法的优化，本文主要从勘探能力和收敛速度两方面着手。首先，通过对优化变量加入混沌扰动策略，扩大搜索区域，促使布谷鸟种群的多样性相应扩大，减少陷入局部最优的概率，提高算法的勘探能力。加入混沌扰动策略后，会降低算法整体的收敛速度，为此引入反向学习算法，通过对精英个体进行反向解运算，得到所有解中表现最优的一个，从而得到最优结果，在一定程度上提高了算法的收敛精度。

在计算过程中，还要考虑从当前群体与反向群体中，如何选择出N个解作为下一次迭代的个体。本文利用群体选择机制，假设p(g)为当前布谷鸟种群，根据反向学习算法得到m个精英个体，并产生与之相对应的反向个体为Eop(g)，计算p(g)∪Eop(g)，从中选择N个精英个体作为下一次迭代的个体p(g+1)。此时N表示精英种群，针对精英个体的数量会对最优解的计算产生一定的局限性的问题，经过反复研究确定，m/N=0.1为最佳参数值，因此本文确定精英个体数量为m/N=0.1。假设FFS为适应度函数评价次数，Max＿FFS表示适应度函数最大评价次数，pm表示执行反向学习算法的概率值，rand∈[0，1]为随机数，以均匀分布的形式存在。在算法实现过程中，δ为随机值，可生成若干个不同的精英个体，从而使得每个精英个体反向学习后都能得到不同的反向解，这个过程可以提高算法的搜索能力。

本文的算法实现过程为：只有满足反向学习的概率值pm条件后，才可执行反向学习运算；如果没有满足条件，仅执行CH-CS。具体描述如下所示：

1)对当前布谷鸟种群p(g)进行反向学习运算；

2)当FFS≤Max＿FFS时，继续计算；

3)如果rand≤pm，停止计算；

4)从种群p(g)中找出m个最优个体构建精英个体种群Xe1，Xe2，…，Xem；

5)对精英个体的搜索范围[xj，yj]进行具体计算；

6)通过计算得到精英个体的反向解，并对反向解求得适应度函数值，组建反向种群Eop(g)；

7)从p(g)∪Eop(g)中选择N个最优个体作为下一代种群p(g+1)；

至此实现基于反向学习的布谷鸟算法优化搜索。

4 仿真研究

为验证本文方法提出的布谷鸟优化算法的搜索性能，将本文方法与文献[1]、文献[2]方法进行对比实验。实验选取如表1所示的四个函数作为实验测试内容，其中，F1、F2表示单峰函数，F3、F4表示多峰函数。为了保证实验结果的公平性，对三种方法的参数进行了统一设定：

表1 测试函数

固定不可变参数：布谷鸟种群数量为30，精英个体的第D维向量为20，维度范围为[-20，20]，迭代次数最大值为5000，收敛精度为10-5。可变参数：布谷鸟的蛋被其它鸟类发现的概率为0.05%，Levy flight的步长缩放因子为0.1，控制因素为1.3。本文方法参数：比例因子为150，单向位置搜索最大数量为15。

表1中各表达式的理论最优值为0。用三种方法分别对上述表达式进行实验测试，结果如表2所示。

表2 三种方法仿真对比结果

从表2中可以看出，较其它两种方法相比，不管是单峰函数还是多峰函数，本文方法都取得了更优的结果，总体上提升了解的质量，尤其是在F3函数上更是得到了全局最优解。

为了进一步验证三种方法改进后的性能，分别测试不同方法下单峰函数和多峰函数的最优值，得到图2所示的三种方法对五个函数的寻优收敛对比图。

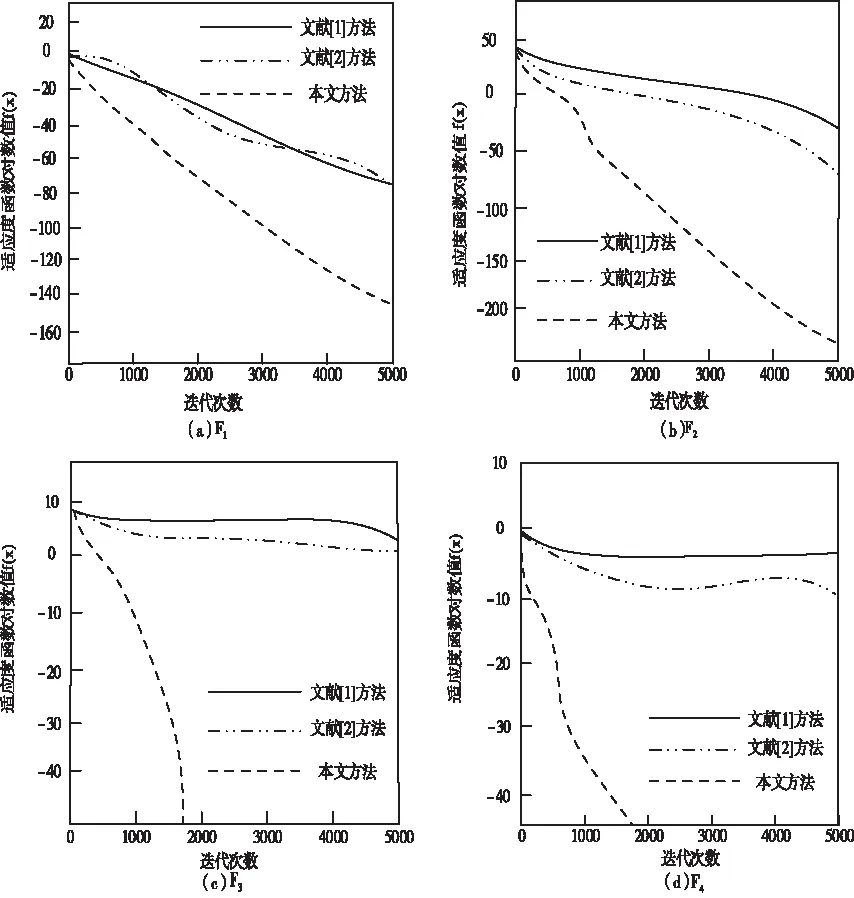
图2 三种方法寻优收敛曲线图

从图2中可以看出，在处理F3和F4复杂的多峰函数时，本文方法较其它两种方法相比，展现出了更高的收敛速度和收敛精度，达到了理论最优值；并且在函数的收敛过程中，本文方法比其它两种方法的寻优收敛曲线斜率更小。这是因为本文引入了反向学习算法，通过对精英个体进行反向解运算，搜索出所有解中的最优解，进一步优化布谷鸟算法性能。综上所述，本文方法较现有方法相比，在布谷鸟算法的搜索能力方面得到了有效提升。

5 结论

由于标准布谷鸟算法在处理复杂的多峰函数时，通常表现出过低的收敛精度和搜索能力，因此，本文提出了基于反向学习的布谷鸟算法优化搜索方法。

1)本文方法主要从以下两点进行优化：第一点是在计算过程中加入混沌扰动策略，扩大算法的搜索范围，从而使布谷鸟种群也得到了扩大，提高了寻优效率；第二点是加入精英反向学习策略，在进行寻优时仅针对精英个体求反向解即可，扩大了搜索空间范围，使得最终结果更接近于最优解。在迭代计算后期，加入混沌扰动策略，在一定程度上还提升了算法整体的勘探能力和开采能力。

2)仿真测试结果表明，本文方法在单峰函数和多峰函数中，均取得了全局最优解，单峰函数F1、F2中，F2取得了全局最优输出值为0.38；多峰函数F3、F4中，F3取得了全局最优输出值为0.00；

3)下一步的研究过程中将把优化后的布谷鸟搜索算法应用到相关领域进行验证，在实际应用过程中进一步提升基于反向学习的布谷鸟算法的搜索性能。