基于改进LLE算法的手势特征提取研究
2022-01-22刘承启
张 翔,席 奇,刘承启
(1.景德镇学院信息工程学院,江西 景德镇 333000;2.南昌大学,江西 南昌 330029)
1 引言
近年来,人机交互逐渐应用在游戏、医疗、机器人等诸多行业。手势识别作为人机交互的一种常见方式,由于其具有多样性、差异性、不稳定性等特点[1],建立人机交互的手势识别系统成为研究的热点。大量学者通过各种各样的方法实现对手势特征的提取。文献[2]基于改进的YCbCr颜色空间模型对手势区域进行提取,并按照手势图像的宽度和高度以及手指个数对手势识别进行粗分类,再将由Hu矩和傅里叶函数构建的融合特征输入BP神经网络中进行识别,实验结果表明,该方法的手势识别率较高,但该方法对光照较为敏感,需要进一步完善。文献[3]通过对梯度方向直方图和二值模式特征的提取和融合,加强对手势特征的描述,并将融合特征输入SVM中进行识别,实验结果表明,该方法可识别多种手势,然而需要对网络模型进一步优化,提高对手势特征的识别率。文献[4]通过手指个数、距离以及手指夹角对手势特征进行建模,并利用分层方法将手势识别的较多类别转化为较少类别,以识别结果为依据完成手势的特征提取,实验结果表明,该方法具有较高的准确率,但该方法对于复杂手势的识别率较低。
针对以上研究成果,本文提出基于改进LLE算法的手势特征提取方法。通过对手势特征数据集中某个数据点处的邻近数据构成局部线性关系,再对这些数据进行重构误差最小化处理,求出映射矩阵,把多特征空间维度的手势特征样本数据映射到低维度空间中。
2 改进LLE算法分析
LLE是一种非线性降维思想控制的方法[5-6],其通过相互结合的局部线性关系描述全局非线性关系。LLE算法的降维过程主要由两步组成。首先,假定LLE算法在较小的局部空间内为线性的,Xlog={xlog_1,xlog_2,xlog_3,…,xlog_N}表示在空间RW内的第N个样本数据集合,W表示数据集合的维度,通过数据点xlog_i处的klog个相邻数据表示局部线性情况。然后,对由klog个相邻xlog_i数据组成的重构误差进行最小化,计算局部重建的权值矩阵。重构误差公式可表示为

(1)
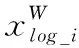
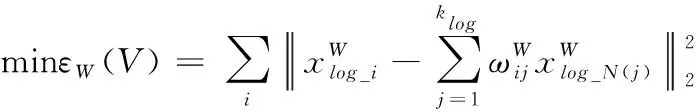
(2)
将εW(V)改写为矩阵形式,公式可表示为

(3)
并且局部重建权值矩阵满足
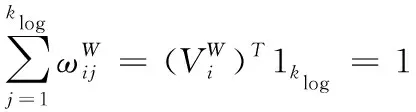
(4)
其中,1klog表示klog维的全1向量。当求解重构误差最小化问题时,用拉格朗日乘子算法将目标函数优化,公式可表示为
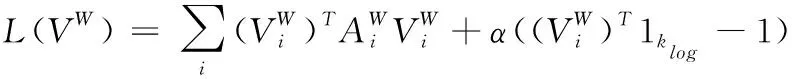
(5)
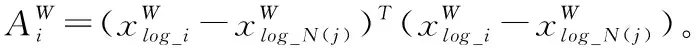

(6)
基于多维空间的分析可以得出新的局部重建权值矩阵,为了使局部线性关系能满足低维数空间,假定多个样本数据在低维数空间中的投影用Ylog={ylog_1,ylog_2,ylog_3,…,ylog_N}表示,Ylog保持了高维数空间的原本属性,通过类比用拉格朗日乘子算法对低维数空间Ylog上的目标函数采取优化,公式可表示为
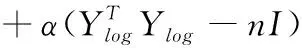
(7)
对目标特征Ylog求导,使导数为0,可以得出(I-V*)T(I-V*)Ylog=αYlog,由此可知目标特征Ylog就是矩阵N=(I-V*)T(I-V*)所对应的n维空间内n个最小特征值构成的矩阵。
通过对手势识别采集的样本数据,进行重新计算可获得重建权值系数,但这样不仅需要大量的存储空间,还影响手势识别的速度。因此假定输入样本空间与目标特征空间满足如下关系
Ylog=GTXlog
(8)
其中,G表示Xlog与Ylog之间的映射矩阵,且G=(G1,G2,G3,…,GW)T;GW表示第W维数空间对应的映射矩阵,且GW∈RhW×n;hW表示第W维数空间的向量维度;n表示Ylog的输出维度。因此只需求解出映射矩阵G,便可以得出手势识别样本数据的目标特征空间映射结果,最小化问题用公式可表示为
minε(Ylog)=tr(GTXlog(I-∑ρWVW)T
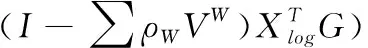
(9)
其中,ρW表示不同特征空间样本数据的权重值。通过优化重建权值矩阵的权重值,可以评估手势识别样本数据的重要程度,提高算法的适用性,但由于在推导过程中,由于一些无效样本数据的引入,大大影响了特征融合的结果。因此,在LLE算法的基础上,通过引入优化目标项的方法,对式(9)的最小化函数采取进一步的优化,公式可表示为
minε(Ylog)=tr(GTXlog(I-∑ρWVW)T
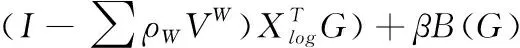
(10)
其中,B(G)表示优化目标;β表示平衡系数。当ylog_i和ylog_j为同一类样本时,它们之间的距离会足够小,样本ylog_i和ylog_j之间满足

(11)

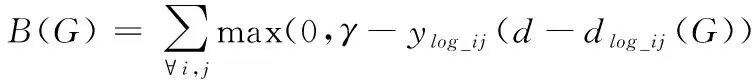
(12)
其中,dlog_ij(G)表示样本ylog_i和ylog_j之间的距离。通过对优化目标的求解,可以得出多特征融合算法的优化目标函数,用公式可表示为
minε(Ylog)=tr(GTXlog(I-∑ρWVW)T

(13)
由式(13)可知,很难求解出映射矩阵G,因此本文通过固定变量的方法,对式(13)中的两个变量进行优化。固定矩阵G,则B(G)为一个常数,多特征融合算法的优化目标函数用公式可表示为
minε(Ylog)=tr(GTXlog(I-∑ρWVW)T
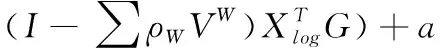
(14)
从机器学习角度分析,求解最小化问题实际上是不断使损失函数最小化的过程,从而得出映射矩阵G,最后只需通过映射操作,便可以把多特征空间维度的手势识别样本数据映射到低维度空间中。
3 手势特征建模
在研究手势特征的运动过程中,手形特征和手势轨迹特征起着至关重要的作用。当手势动作较快时,手势的运动轨迹起着主导作用;当手势动作较慢时,手形信息起着主导作用。针对手势特征的提取,可以采用运动速度提取手势片段。首先需要选择一个速度阈值用来选择关键手势的图像帧,公式可表示为
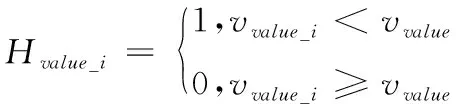
(15)
其中,Hvalue_i表示第i帧手势图像的关键片段;vvalue_i表示每帧手势图像的运动速度;vvalue表示手势图像的速度阈值。由于手势运动速度是一种连续的渐变函数关系,因此通过采用加权平均方法,对速度阈值进行处理,公式可表示为

(16)
其中,N表示手势图像中总共帧的数量;τ表示手势的平均速度系数。获取到关键手势图像后,需要根据图像的像素值计算对应手势图像中的平均像素值,公式可表示为

(17)
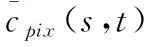

(18)
其中,Lx和Lfin_wri分别表示归一化后和需要归一化的手势距离;min(Lfin_wri)表示指尖到手腕的最小距;max(Lfin_wri)表示指尖到手腕的最大距离。随着手势特征维度的增加以及手势特征中存在的冗余特征,会削弱手势特征提取的实时性,因此采用支持向量分类器(SVC)的方法将手势从难以分类的空间映射到高维度的手势空间中。假定训练手势集用S={(xtra_1,ytra_1),(xtra_2,ytra_2),…,(xtra_N,ytra_N)}表示,xtra_i和ytra_i分别表示输入手势样本数据和实际手势标签,那么支持向量分类器的分类过程可表示为

(19)

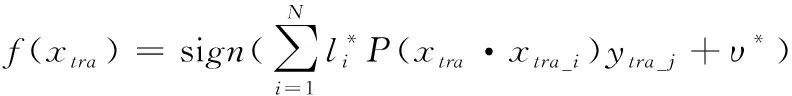
(20)
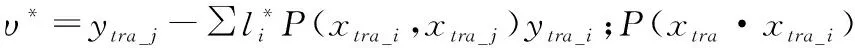
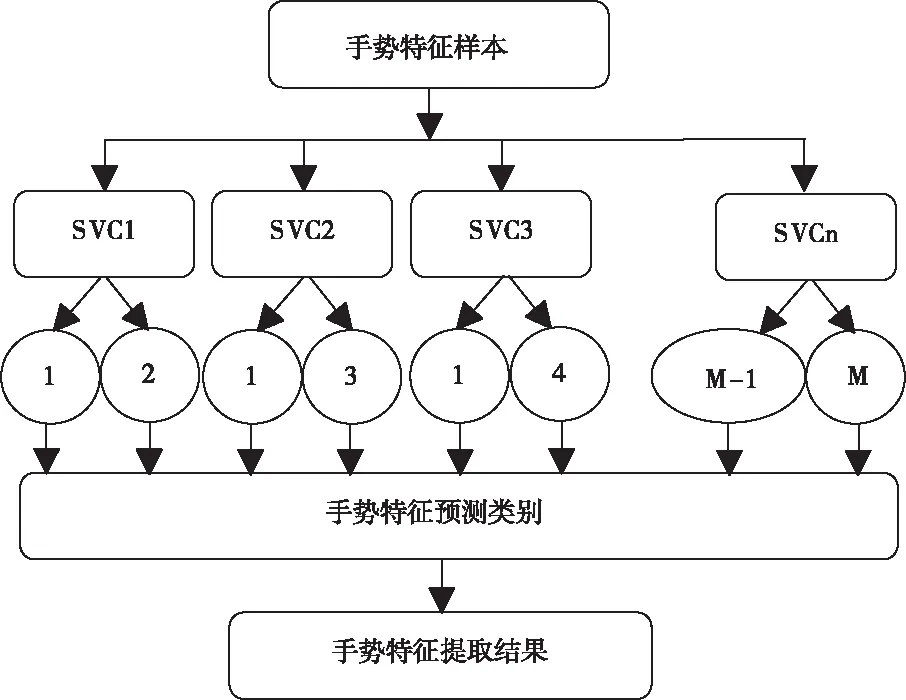
图1 手势特征提取模型
4 实验结果与分析
仿真过程中,为了保证手势的整体动作出现在Kinect摄像机的采集画面中,实验者需要面向摄像机镜头,并保持一定的距离。在进行手势训练过程中,选择5名实验者按照一定的顺序依次做出10种经典手势,并且每种手势依次做10遍,共采集5×10×10个数据作为手势训练的数据库,在数据库中存储了各种手势的手形特征和运动轨迹特征等信息。
在手势特征的动态测试过程中,首先选择3个典型的手势作为待测样本,如图2所示。其中“肯定”的手势主要是手部运动变化;“右转”的手势主要是上肢肢体的运动变化;“启动”的手势中主要是手部和上肢肢体的运动变化。
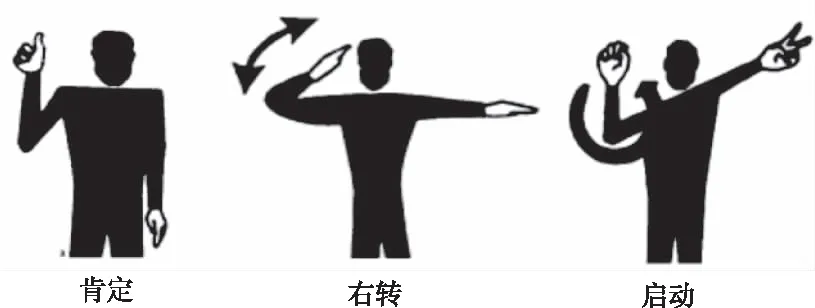
图2 测试手势
实验中获得5×10×3个手势特征待测样本数据,并对这些待测样本数据进行循环测试,直到所有数据都测试一遍,得到特征提取结果如表1所示。
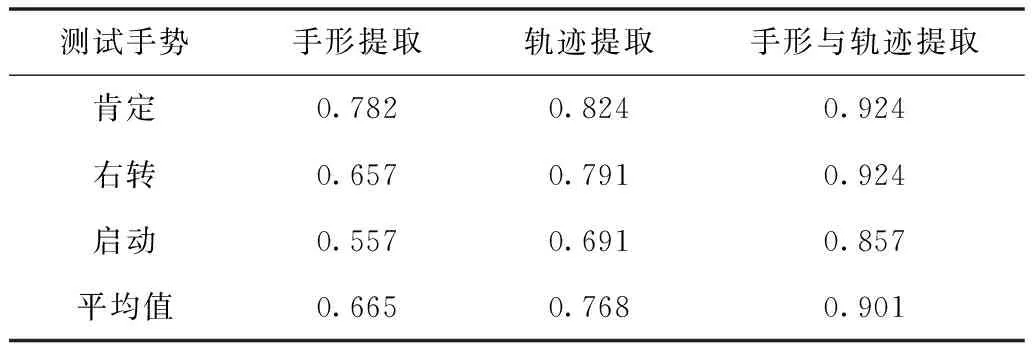
表1 手势特征提取正确率统计表
从表中可以看出,采用单独的手势提取、轨迹提取平均识别率分别为0.665、0.768,识别率相对较低。但对于整体手势特征提取测试数据而言,本文提出的方法均能达到较好的识别效果,平均识别率可达到0.901,表明采用改进的LLE算法可以更好地描述手势特征,验证了本文方法的有效性。
为了进一步验证本文方法对手势特征的提取效果以及手势特征模型的泛化能力,本文采用两种性能度量指标对手势特征进行度量,性能指标分别为查准率和召回率,实验结果如表2所示。
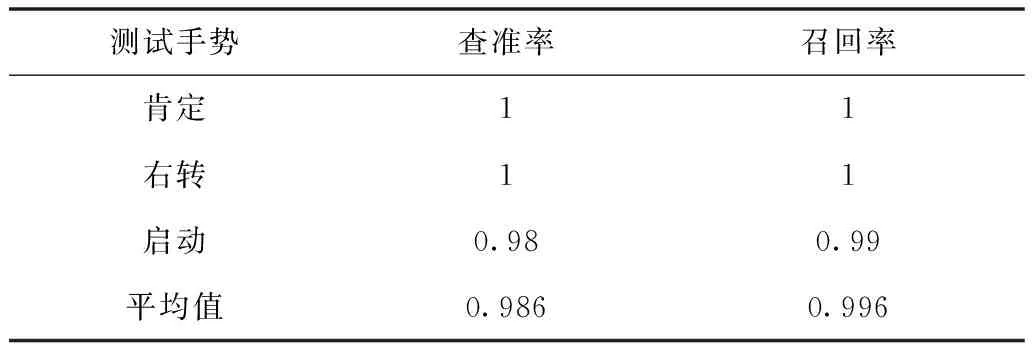
表2 性能度量结果
从表中可以看出,“肯定”和“右转”手势的查准率和召回率可达到1,表明采用本文提出的方法对手势测试集能够正确进行分类,“启动”手势的查准率和召回率依次是0.98和0.99,表明在对手势进行分类过程中,该类型的手势识别性能相对“肯定”和“右转”较弱一些,综合考虑本文方法的泛化性较好。
为了验证本文算法在手势特征提取中的优越性,将本文方法与文献[2]、文献[3]和文献[4]进行实验对比,对比结果如图3所示。
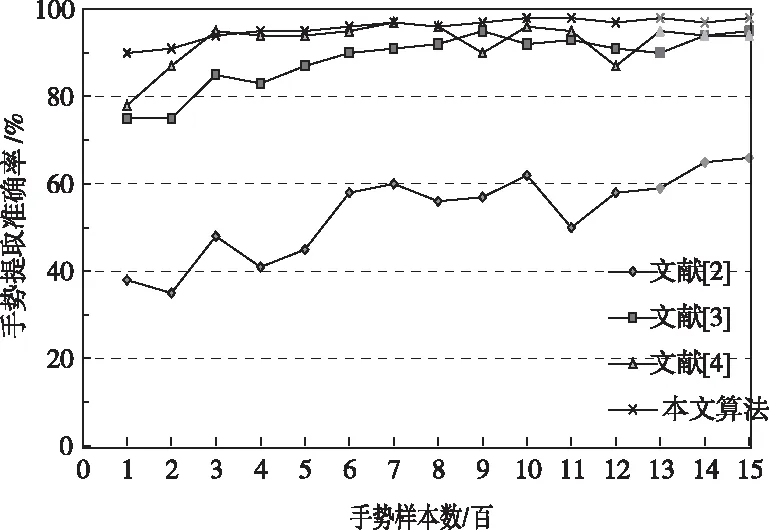
图3 手势特征提取的准确率曲线
从图中可以看出,文献[2]得出的手势特征准确率明显低于其它方法,对手势特征提取的效果不好;文献[3]得出的手势特征准确率在手势样本数据较少时,准确率较低,随着样本数据的不断增多,准确率不断提高;文献[4]得出的手势特征准确率虽然较高,但是随着样本数据的增加,准确率持续波动,不稳定;而本文方法得到的手势特征具有较高的准确率,即使样本数据很少,也具有较好的识别效果,随着样本数据的增加,手势特征提取准确率呈上升的趋势。
5 结束语
本文针对手势特征提取提出了一种基于改进的LLE算法,通过手势样本特征的局部空间重建权值矩阵,实现对多个手势特征空间的度量,同时结合输入与输出特征空间的映射变换矩阵,降低样本空间维度,采用稀疏观察手势描述法对手势特征进行提取。仿真结果表明,采用本文提出的方法对手势特征进行提取,平均识别率可达到0.901,查准率和召回率指标都接近于1,具有良好的泛化性和识别效果。
