基于多方向阈值的超分辨率图像噪声识别仿真
2022-01-22王旭阳刘世健
王旭阳,刘世健
(兰州理工大学计算机与通信学院,甘肃 兰州 730050)
1 引言
目前科技水平飞速发展,图像的分辨率也随之提高,图像中存在的信息逐渐增多,内容也更为庞杂,必须对图像进行去噪处理,如何对图像进行噪声识别就成为了当前该领域热点问题[1-2]。由于当前图像噪声识别方法已经无法对超分辨率图像进行噪声识别,因此,提出一种新型的图像噪声识别方法就变得较为重要[3]。
目前该领域大量学者对其进行了研究,并取得了一定的研究成果,文献[4]提出基于灰度直方图的图像噪声识别方法。该方法首先对图像中的噪声进行整合,利用统计学方法构建数学模型,获取不同噪声的随机矩阵,并将矩阵加载到灰度图像中;最后利用图像中的灰度等级画出直方图中的噪声状态分布对超分辨率图像进行噪声的识别。该方法由于未能利用多方向阈值中的灰度波动局部阈值分割法对图像进行分割,所以导致图像在进行噪声识别覆盖率低。文献[5]提出基于灰狼算法的图像噪声识别方法。该方法首先利用灰狼算法对超分辨率图像中的参数进行寻优处理,以此构建参数的最优模型优化图像中的参数。再根据噪声的分类构建图像的噪声分类器,将优化的参数放入分类器中进行特征分类,以此完成图像的噪声识别。该方法由于未能计算灰度波动曲线中极小值点的最小值与极大值点的最大值,获取极大值与极小值的序号,所以导致图像在进行噪声识别时,识别时间长,识别效率低。为解决上述图像识别方法中存在的问题,提出基于多方向阈值的超分辨率图像噪声识别方法。
2 图像分割
选定一张超分辨率图像,利用多方向阈值中的灰度波动局部阈值分割法对超分辨率图像进行分割。
2.1 获取均值滤波
对选定的图像进行分析,分析后可知,图中留存了许多大小不等尺度的波谷、波峰以及些许椒盐噪声。由于分割时会使图像中的高频符号变得较为敏感,导致图像中高振幅的椒盐噪声无法剔除[6]。所以在对图像进行分割前,首先利用均值滤波模板对超分辨率图像中的椒盐噪声进行剔除,缩减图像中小尺度波谷和波峰的振幅,提高图像分割的精准度。
2.2 一维阈值分割
以水平方向为基准,对超分辨率图像进行一维阈值分割,首先设定灰度图像行号为f(x)=F(x,y),表示该行中所有的像素一维函数,其中x=1,2,3,…,X,X为行中的像素总数。获取的一维灰度函数曲线如图1所示。

图1 一维灰度函数曲线
由图1可知,该曲线是依据图像中若干个波峰与波谷组成的序列,在超分辨率图像的波谷与波峰之间设定一点,这个点的灰度值为图像的局部阈值,将曲线波动边沿上大于局部阈值的像素设为L-1,反之则为0,L是像素灰度级[7]。
利用上述的一维灰度函数获取超分辨率图像的灰度波动曲线,其中每一行的灰度波动曲线如图2所示。
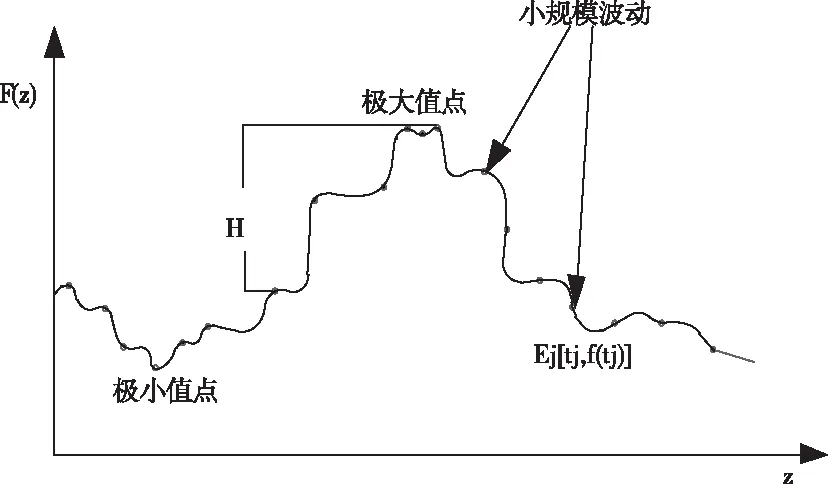
图2 灰度波动曲线图
提取图2中的最小值与最大值作为一维阈值分割的起点。设N为曲线上极值点的总个数,En(n=1,2,…,N)则是曲线上全部极值点,而曲线上最大极值点可以表示为Emax[ci,f(ci)]=arg max{E1[c0,f(c0)],E3[c1,f(c1)],…,En-1[c(n-1)/2,f(c(n-1)/2)]},式中,i为超分辨图像中的极大值点的像素序号,ci为图像中的极大值点像素,f(ci)为图像中像素ci的灰度值。
灰度波动曲线中极小值点的最小值表示为Emin[tj,f(ti)]=arg min{E1[t0,f(t0)],E3[t1,f(t1)],…,En-1[tn/2,f(tn/2)]},式中,j为波动曲线中的极小值点像素序号,tj为波动曲线中的极小值点像素,f(tj)则是波动曲线中像素tj的灰度值。
若Tk=Em是图像分割时的起始波谷点(或为上一个满足阈值条件H的波谷点),极值点的序号则为m,H∈[0,255]。这时,下一个满足阈值条件H的波峰点用Ck+1=Ei表示,需要满足的条件如下式所示
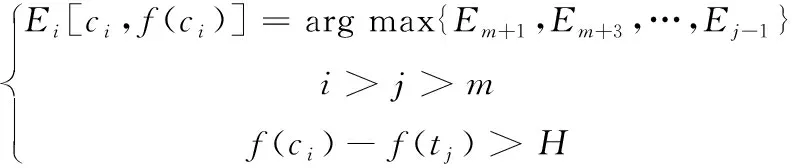
(1)
其中,波动曲线中Ei[ci,f(ci)]的后一个极小值点为Ej[tj,f(tj)],i为极大值点的序号,Ei则是波动曲线中的极大值点[8]。
这时,若Ck=Em为分割图像时的起始波峰点(或为上一个阈值条件H的波峰点),那么下一个满足波动幅度阈值条件H的波谷点Tk+1=Ej需要满足的条件如下式所示
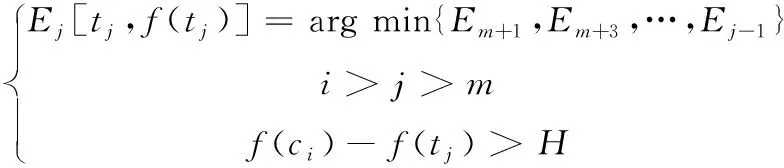
(2)
其中,Ej[tj,f(tj)]后的下一个极大值点为Ei[ci,f(ci)],j为波动中的极小值点序号,Ej则是波动中的极小值点。
利用上述超分辨率图像搜索过程持续对图像进行搜索,以此完成对图像中全部波峰点与波谷点的定位。
基于定位后的波峰点、波谷点顺序,对超分辨率图像进行局部的阈值分割。
设[Tk[tj,f(tj)],Ck+1[ci,f(ci)]]是图像需要分割的区间,给定浮动参数ξ,ξ∈[0,1],那么局部阈值ht的表示就如下式所示
ht=ξ×[f(tj)-f(ci)]+f(ci)×(1-ξ)
(3)
对于曲线p∈[tj,ci]上的点P[p,f(p)],当f(p)>ht时,P属于目标,否则P为背景。若曲线的头部和尾部存在于极值点的边界之间,便可直接与其邻近的极值一起进行处理。当曲线上所有的极值点序列搜索完毕,就完成了图像的一维阈值分割。
3 噪声识别
将分割后的超分辨率图像中的部分样本数据进行归一化处理,以此防止图像差异对识别的结果造成影响。依据以下流程对超分辨率图像的噪声进行识别:
1)不显著系数的能量比
基于小波变换原理,将超分辨率图像中的噪声信号表现在各个尺度信号的高频信号中。再利用小波变换后的高频系数直方图与曲线拟合图的不同特征来识别图像的噪声受干扰类型[9]。超分辨率图像经过小波分解后,各子带上都携带了图像中的不同特性,其中的图像噪声则主要集中在高频子带中,再对高频子带进行分析,以此识别噪声类型。
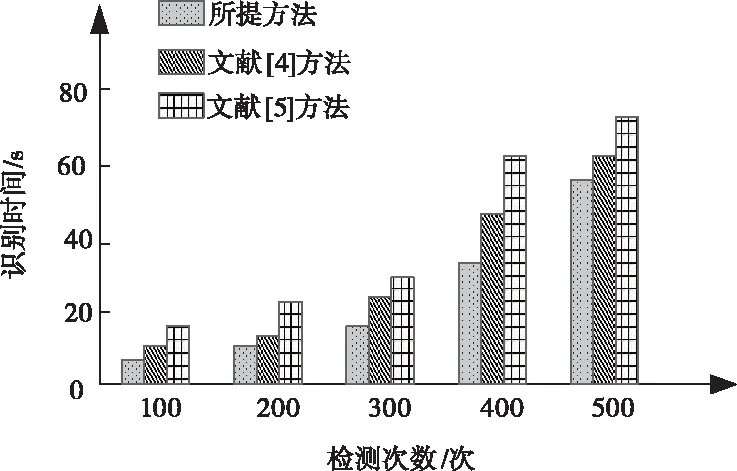
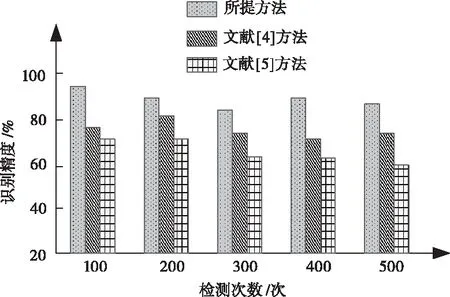
设高频子带系数矩阵为D(i,j),再按照系数幅值绝对值的大小来划分较小系数DT(i,j)={|D(i,j)|,|D(i,j)| (4) 其中,munT的目的是为了满足较小系数条件的系数个数,mun则为高频系数中高频子带的总个数。在获取该项数值时,将含有噪声的超分辨率图像的三维影像展开分为3个平面图像,并对其进行小波分解提取图像中的高频信息,以此获取高频系数的较小系数能量比。 2)图像的噪声能量熵分布 由于图像中亮度可以反映信号的强弱,信息熵可以反映图像中的信息量,所以将获取的高频系数能量比与图像能量熵相结合对图像中的信息冗余与噪声能量紊乱提供衡量指标[10]。利用噪声能量熵分布的梯度特征平面Zernike矩,提高超分辨率图像的识别效果。过程如下式所示 (5) (6) 由此,利用Terzopoulos与Gossard构建自由曲面的一般模型,对图像中噪声曲面的曲率变化率、弹性变化率、边界法矢、曲面离散率、外载荷修正量等特征值进行分析。模型为下式所示 2Wf(μ,ν)]dμdν (7) 式中,W为获取的参数(μ,ν)曲面,图像曲面沿着μ,ν方向的一、二阶偏导矢分别为Ww、Wν、Wμ、Wμμ,而它们的混合偏导矢为Wμν,α,β为材料的特性参数,而f是用来改变曲面形状的外载荷[11]。在大部分情况下,材料参数与外荷载的影响不予考虑,直接赋值即可α,β=1,f=0。 噪声曲面的曲率变化率如下式所示 (8) 其中,ei,ej为噪声曲面的主方向,ki,kj为沿着主方向的主曲率。 噪声曲面中μ,ν方向的弹性变化率如下式所示 (9) 式中,W是以μ,ν为参数的噪声曲面,噪声曲面沿着μ,ν方向的一、二阶偏导矢分别为Ww、Wν、Wμ、Wμμ,α,β为曲面中的给定参数,而f(μ,ν)则是曲面给定的矢量函数。 噪声曲面的曲面边界法矢如下式所示 (10) 式中,曲面上的任意三个点组合在一起都可成为图像的三角曲面法矢[12]。 图像中噪声曲面的曲面离散率如下式所示 (11) 式中的Sμμ(μi,ν),Sνν(μ,νj)是噪声曲面在μ,ν两个方向上的二阶导数。 曲面的外载荷修正量如下式所示 (12) 式中,曲面沿着μ,ν两个方向控制B样条曲线的分别为Bi,su(μ),Bj,sν(ν)。 最后将Ca到Ch这八组特征值整合到一起,组成一组特征向量,如下式所示 C=[CaCbCcCdCeCfCgCh]T (13) 最后将特征向量作为神经网络分类器的输入向量,对超分辨率图像中的噪声进行分类、识别,由此实现超分辨率图像噪声识别。 为了验证基于多方向阈值的超分辨率图像噪声识别方法的有效性,需要对此方法进行测试。采用的操作系统为Windows7、120G硬盘、CPU为Pentium(R)Dual-Core、内存为8G、处理器为酷睿i5,在MATLAB R2013B环境中进行仿真对比实验。分别采用所提方法、文献[4]方法、文献[5]方法进行测试; 设定检测次数为500次,利用同一型号的处理器对所提方法、文献[4]方法以及文献[5]方法的超分辨率图像噪声识别时间进行对比,对比结果如图3所示。 图3 超分辨率图像噪声识别时间对比结果 分析图3可知,随着检测次数的增加,不同方法的识别时间随之增加,当检测次数为500次时,文献[4]方法的识别时间为63s,文献[5]方法的识别时间为74s,而所提方法的识别时间为58s,由此可知,所提方法的超分辨率图像噪声识别时间较短。因为所提方法在识别噪声前,利用了多方向阈值中的灰度波动局部阈值分割法,对超分辨率图像进行了一维阈值的计算,并将获取一维阈值的图像进行了分割处理,从而缩短噪声的识别时间。 在此基础上,对所提方法、文献[4]方法以及文献[5]方法的图像识别覆盖率进行对比,对比结果如图4所示。 图4 超分辨率图像识别覆盖率对比结果 分析图4可知,所提方法的识别覆盖率明显高于文献[4]方法和文献[5]方法。这主要是因为所提方法在识别噪声初期利用一维灰度函数曲线及灰度波动曲线对图像中的波谷、波峰及局部阈值进行计算,获取图像的极值点序列,从而使所提方法在噪声识别时,能够覆盖超分辨率图像,提高识别覆盖率。 基于上述测试结果,对所提方法、文献[4]方法和文献[5]方法的图像噪声识别精准度进行测试,测试结果如图5所示。 图5 超分辨率图像噪声识别精度对比结果 分析图5可知,当检测次数为500次时,文献[4]方法的平均识别精度为78%,文献[5]方法的平均识别精度为72%,而所提方法的平均识别精度为93%,由此可知,所提方法的图像噪声识别精度高于文献[4]方法及文献[5]方法。这主要是因为所提方法利用了灰度波动曲线将波峰与波谷整合为一组序列,通过计算序列边沿点,获取图像的局部阈值并以此对图像进行分割,依据分割图像特征值,识别超分辨率图像噪声,能够有效提高噪声识别精度。 针对当前方法在噪声识别时,存在的识别时间长,精准度和覆盖率低的问题,提出基于多方向阈值的超分辨率图像噪声识别方法。多方向阈值中灰度波动局部阈值分割法对图像进行分割。将分割后的超分辨率图像中的部分样本数据进行归一化处理,分析分割后图像的特征值,并将特征值整合成一组特征向量放入分类器中进行计算,以此完成超分辨率图像的噪声识别。所提方法能够有效缩短超分辨率图像噪声识别时间,提高识别覆盖率和识别精度。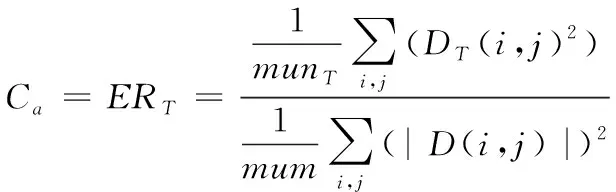
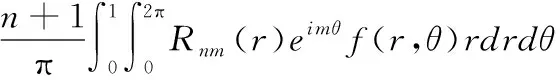
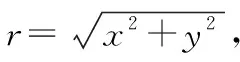
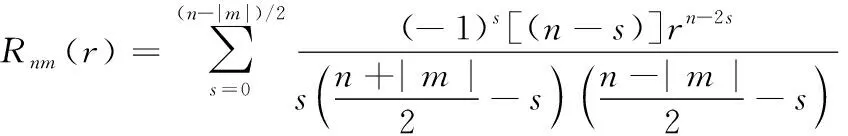
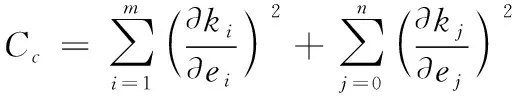
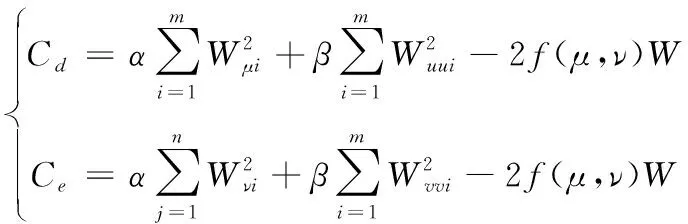
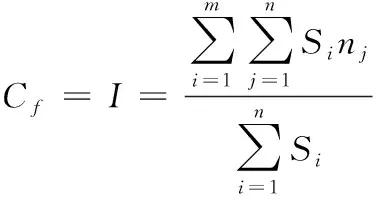
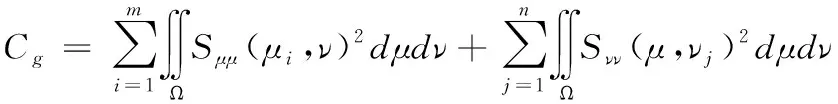

4 实验分析

5 结束语
