基于ADAMS的供氧传动机构故障诊断与优化
2022-01-22孙捷夫
孙捷夫,杨 巍,潘 海
(1.沈阳飞机工业(集团)有限公司,辽宁 沈阳 110000;2.哈尔滨工程大学,黑龙江 哈尔滨 150000)
1 引言
供氧传动机构是某型号飞机氧气系统的重要功能附件,在实际工况下,该产品将外力驱动转化为位移行程控制氧气开关的开启与闭合,若供氧传动机构的行程性能不满足设计要求,直接导致氧气开关无法正常开启或开启范围异常,使飞机驾驶舱供氧不足,对驾驶员生命安全产生严重的安全隐患。
在实际生产制造中,由于制造精度和装配误差等因素的影响,供氧传动机构的行程指标难以稳定可靠的满足公差要求。生产现场现有解决方法是对分解后的组成零件逐个测量,将实测尺寸偏极限尺寸的零件替换为实测尺寸为理论尺寸的同类零件。该方法从根本上是以提高零件的制造精度改进装配效果,不仅效率低、成本高,且缺少量化分析和指导性工艺对策,对行程指标的改进收效甚微。
关于飞机供氧传动机构或类似的飞机功能附件的故障诊断和优化研究的公开成果较少,但近年来,采用虚拟仿真技术进行产品故障诊断和优化研究取得了一定成果:解梦涛等[1]针对航空发动机放气活门机构摇臂断裂故障,利用动力学仿真软件ADAMS和有限元仿真软件ANSYS联合仿真分析,实现故障再现并给出优化改进建议;聂青等[2]基于ADAMS软件对飞行器空气舵传动环节的系统间隙进行敏感性分析,探究各零件对系统间隙的影响规律,为优化设计提供理论支撑;刘广等[3]应用ADAMS软件对单侧弹射发射系统建立刚柔耦合虚拟仿真模型,并赋予实际工程数据完成故障复现;陈材等[4]以动力学仿真软件ADAMS为平台,针对机械装备中不同的机械故障研究对应的故障注入方法,实现机械装备毁伤效果精确评估;王钰龙等[5]在ADAMS软件中建立飞机起落架虚拟样机,针对实际生产中发生的变形、卡滞等现象进行仿真故障复现,探究问题形成原因并给出改进建议;胡明等[6]基于ADAMS/insight对折叠翼展开机构进行工作可靠性的评估与分析,为故障诊断和优化改进奠定基础。上述文献均基于ADAMS软件实现不同对象的故障复现和优化设计。
本文以降低某型号飞机供氧传动机构行程指标故障率为目标,通过分析供氧传动机构运动原理提取影响行程指标的影响因素,基于ADAMS软件建立虚拟样机模型,以故障产品实际数据为基础进行故障复现,验证模型的可行性,通过单因素敏感性分析探究各设计变量对行程指标的影响规律,进行故障诊断,从以仿真为方法的优化设计和以工程实践为考虑的工艺控制两方面入手,全面降低供氧传动机构行程指标的故障率。
2 运动原理分析
供氧传动机构主要包括壳体、摇杆、凸耳、套筒、滑块、支撑块、弹簧、支座和钢丝,结构示意图如图1所示,零件之间的连接关系如图2所示。供氧传动机构主要运动原理为:外力驱动摇杆绕壳体铰接点转动,摇杆带动凸耳推动滑块在套筒中水平移动,滑块水平运动带动钢丝在水平方向产生一定位移,与其它产品配合实现供氧器的开启与闭合,支撑块、弹簧和支座起到辅助支撑作用。
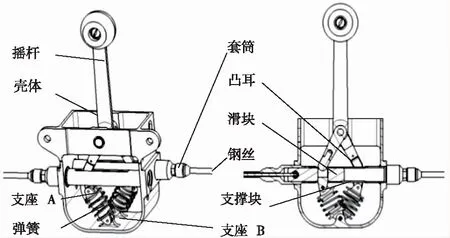
图1 供氧传动机构结构示意图
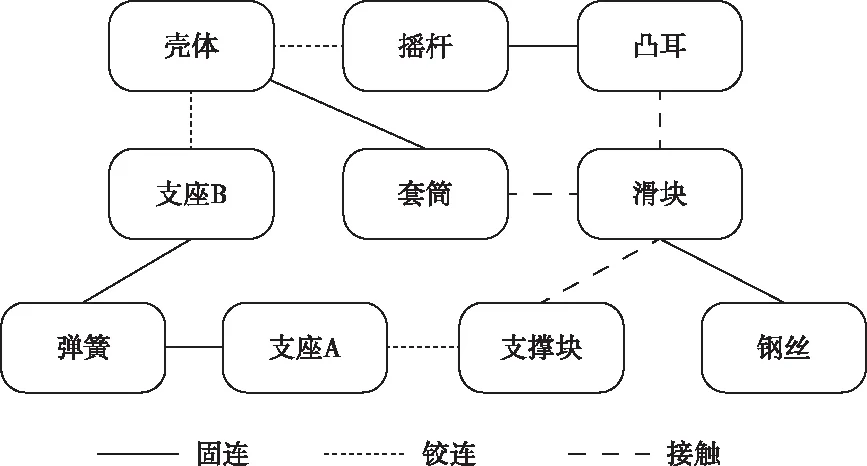
图2 供氧传动机构零件连接关系示意图
由于摇杆与凸耳为固定连接,且运动方式相同,为方便分析,后续将摇杆和凸耳的组合体统称为摇杆。供氧传动机构运动分解如表1。

表1 供氧传动机构运动分解
滑块在左右极限位置的距离即为滑块行程,为满足供氧传动机构使用性能,要求摇杆在用2s完成表1的一个中完整运动周期时,滑块行程需在(27±1)mm范围内。
滑块的运动依靠摇杆的推力驱动,摇杆与滑块的几何参数是影响滑块行程的重要因素,对滑块行程形成原理进行分析。如图3所示,O点为摇杆与壳体的铰接转动点,A为摇杆与滑块左极限位置接触点,B为摇杆与滑块右极限位置接触点,A′为滑块处于右极限位置时滑块左壁上与B点对应的位置,O′为O点在AB连线上的垂点。

图3 摇杆与滑块运动示意图
滑块的行程可按如下公式分析:
S=AA′=AB-A′B
(1)
AB=2AO′
(2)

(3)

(4)
AC=(W-2R)/2
(5)
OC=L
(6)
OO′=H-D/2+C
(7)
A′B=D1
(8)
将(2)-(8)代入(1)可得式(9)
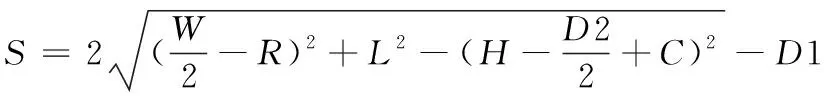
(9)
式中,S:滑块在一个运动周期内行程;W:摇杆宽;R:摇杆圆角半径;L:摇杆长;H:转动点O与滑块轴线距离;D2:滑块直径;C:滑块槽倒角直边长;D1:滑块槽长。
3 故障复现仿真分析
3.1 参数化建模
经过对供氧传动机构的运动原理分析,可知影响滑块行程的主要因素包括摇杆宽W、摇杆圆角半径R、摇杆长L、转动点O与滑块轴线距离H、滑块直径D2、滑块槽倒角直边长C、滑块槽长D1。为研究上述因素对滑块行程的影响,基于动力学仿真软件ADAMS,将上述7个参数作为设计变量,取值范围参考实际工程中的公差要求,完成摇杆和滑块的参数化建模,其余零件在第三方软件建模后导入ADAMS软件中[7],并按图2连接关系进行装配,建立供氧传动机构参数化模型。

表2 参数化模型设计变量及取值范围

图4 供氧传动机构参数化虚拟样机模型
3.2 故障复现仿真
对在生产现场的一个行程超差的故障产品进行分解,对各设计变量的尺寸进行实际测量,实测值如下表所示。

表3 故障产品实测值
从上表可知,故障产品各设计变量均满足公差要求,但滑块行程超差。将被测要素的实测值赋予参数化模型的设计变量中,仿真进行故障复现,以水平向右为正方向,滑块位移曲线如图5所示。

图5 故障产品滑块位移随时间变化曲线
图5中各关键点坐标如下:A(0,-3.5)、B(0.02,-3.5),C(0.41,-6.195),D(0.59,-6.195),E(1.46,22.995),F(1.64,22.995),G(2,1.26),图5所反映的滑块运动曲线轨迹与表1的机构运动过程基本相符,曲线最高点与最低点纵坐标之差即为仿真得出滑块在2s内的行程29.19mm,与故障产品实测行程29.22mm非常接近,完成故障复现,验证了模型与实际情况的符合性满足要求。同时由仿真得出滑块在2s使尚未回到初始位置,没有形成完成一个完整的运动周期,进一步验证了该故障产品行程超出公差上限。
3.3 可靠性仿真
在实际工程中,由于公差累计导致滑块行程会有一定概率的超差,为量化评估产品故障率,现基于ADAMS/insight模块对参数化模型进行可靠性仿真[8-9]。
基于实际生产数据,各设计变量均值为理论值,取值范围如表2所示,将滑块行程作为响应因子,仿真次数为100次,利用蒙特卡洛算法进行可靠性仿真,仿真结果统计如表4所示。
根据表4的仿真结果统计,按现有设计和加工情况,滑块实际行程相对理想行程呈现偏大趋势,供氧传动机构虚拟仿真故障率为18%。
4 故障诊断仿真分析
4.1 设计变量敏感性分析
为探究各设计变量对滑块行程的影响规律,对各设计变量对滑块行程的敏感性进行分析。基于ADAMS试验设计模块[10-11],逐个将设计变量在公差范围内取5个水平,其它设计变量取理论值进行单变量仿真分析,设计变量取值情况如表5所示。

表5 敏感性分析设计变量取值

图6 不同摇杆长度对应滑块行程
图6为摇杆长L取表5中5个水平值仿真得出的滑块行程随时间变化曲线,随着摇杆长度增加,滑块行程单调递增,在ADAMS软件中仿真得出敏感度为72.431,类似方法对其余6个设计变量进行单因素敏感性仿真计算,计算结果如表6所示。
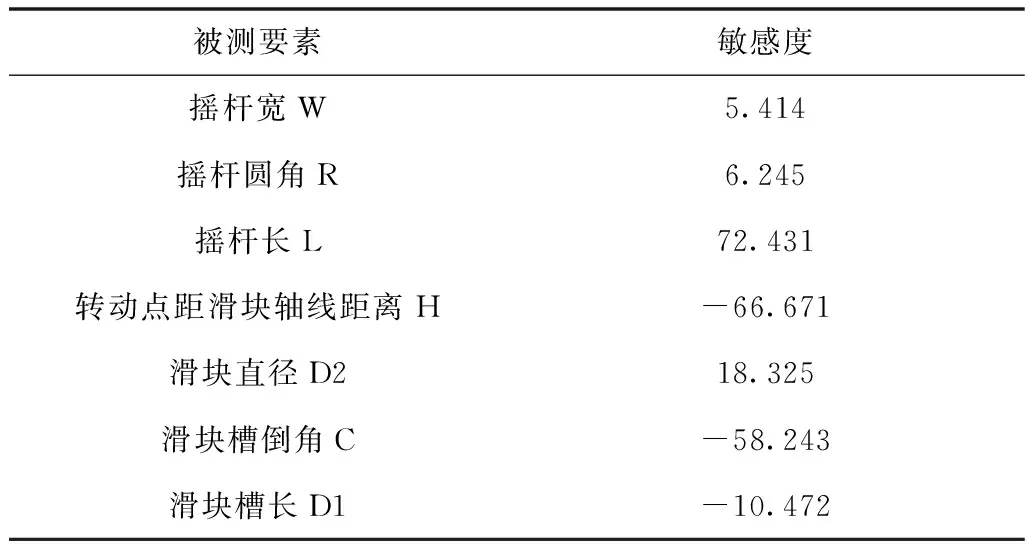
表6 设计变量敏感度分析
敏感度为正值代表该设计变量与滑块行程正相关,敏感度为负值代表该设计变量与滑块行程负相关,由表6可知,滑块行程随摇杆宽W、摇杆长L、滑块直径D2增加而增加,滑块行程随摇杆圆角R、转动点距滑块轴线距离H、滑块槽倒角C、滑块槽长D1增加而减小;同时各设计变量对滑块行程影响程度排序为:摇杆长L>转动点距滑块轴线距离H>滑块槽倒角C>滑块直径D2>滑块槽长D1>摇杆圆角R>摇杆宽W,且摇杆长L、转动点距滑块轴线距离H和滑块槽倒角C的敏感度明显大于其它设计变量。
4.2 故障诊断仿真
基于敏感性分析得知各设计变量对滑块行程的影响规律,现对表3所述的实际故障产品进行故障诊断,故障产品的行程超出设计要求的上限,且正相关变量摇杆长L的实测值大于理论值,负相关变量转动点距滑块轴线距离H和滑块槽倒角C均小于理论值,上述三个设计变量的实际加工情况均有使滑块行程变大趋势,现将这三个设计变量在参数化模型中设定为理论值,其它设计变量按表3中实测数据设置进行仿真,原故障产品的滑块行程由29.22mm降低至27.49mm,仿真结果符合设计要求。

图7 故障产品改进前后滑块位移曲线
为进一步验证改进效果,将摇杆、滑块和壳体零件的摇杆长L、壳体转动点距滑块轴线距离H和滑块槽倒角C按理论值加工,其余尺寸按表3中故障产品实测值重新制造,装配后实测滑块行程为27.54mm,该实测值与仿真结果相近且满足设计要求,因此,表3所述的故障产品行程超差的主要原因可判定为摇杆长L、转动点距滑块轴线距离H和滑块槽倒角C的偏差累计。
5 优化设计及工艺控制
为提高产品可靠性,在ADAMS/insight模块进行优化设计[12-13],设计变量为摇杆长L、转动点距滑块轴线距离H和滑块槽倒角C,约束条件按表2的公差范围设定,优化目标为滑块行程为27mm,优化方法选用ADAMS软件中集成的OPTDES-GRG算法,终止条件为与目标值差值小于等于0.02mm。
优化后设计变量优化值如表7所示,滑块行程为26.9949mm,如图8所示。
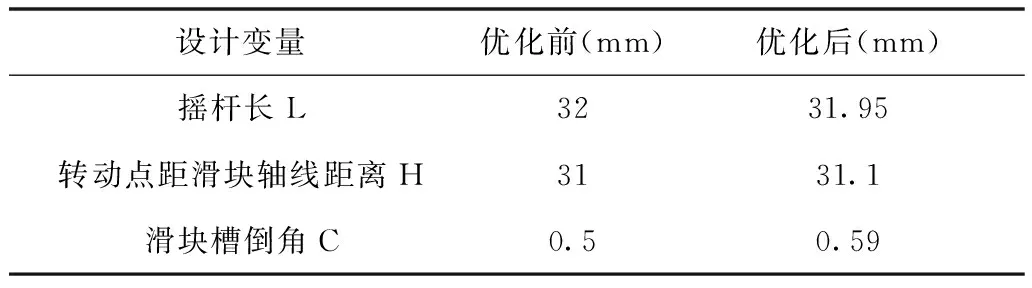
表7 优化结果

图8 优化后滑块位移曲线
为使研究成果落实到实际生产中,综合考虑公差设计原则和实际制造情况,对相应尺寸理论值及公差进行调整,同时保证调整后设计变量取值范围在原设计公差范围内,如表8所示。
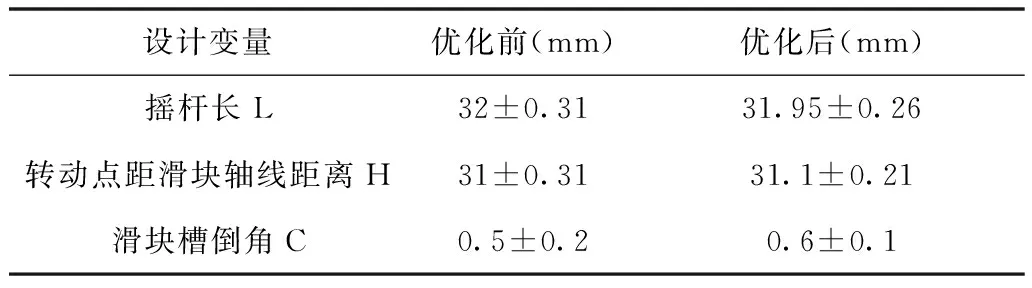
表8 尺寸理论值及公差调整
基于表8中优化后的理论值和公差范围,在ADAMS/insight模块对优化后模型进行可靠性仿真,仿真次数为100次,仿真结果统计如表9所示。

表9 优化后可靠性仿真结果统计表
优化后,产品通过可靠性仿真计算将故障率由18%降低至4%。
为进一步降低产品行程指标故障率,给出工艺控制指导方法:
1)改变结构,控制摇杆长度尺寸。将凸耳伸出摇臂长度减小2mm,在摇臂和凸耳之间增加厚度2个厚度1mm的铝合金垫片,通过调整垫片数量保证摇杆L总长,以调整滑块行程。
2)提高精度,控制转动点距滑块轴线距离。提高壳体孔的加工与转动孔之间的位置精度,以及与滑块配合的衬套的孔轴同轴度。
3)工序调整,控制滑块槽倒角尺寸。在滑块零件机加阶段,先将滑块槽倒角加工至0.5mm,允许在装配阶段根据需要配合锉修至要求尺寸。如装配后滑块行程大于上限要求,由于摇杆长度敏感度较大,通过调整摇杆垫片数量仍然难以将滑块行程控制在合格范围内,则允许锉修滑块槽倒角,以减小滑块行程至公差范围内。
6 结论
1)以某型号飞机供氧传动机构为对象,基于对其滑块行程形成原理分析结果,建立参数化虚拟样机模型,通过仿真完成故障复现,并验证了模型精度满足实际要求。
2)基于敏感性分析,得出各设计变量对行程指标的影响规律,通过仿真模拟和实际验证,得出摇杆长L、距离H、滑块槽倒角C的偏差累计是导致行程超差的主因。
3)以行程为目标对主要设计变量的取值范围进行优化设计,优化后摇杆长L、距离H、滑块槽倒角C的的取值范围分别为31.95±0.26、31.1±0.21、0.6±0.1,通过仿真分析,优化后滑块行程故障率由18%降至4%,同时针对三个主要设计变量分别给出实际工艺控制方法,具有实际工程指导意义。
