先张法预应力混凝土应力传递解析

成 晟

(泰州市公路事业发展中心，泰州 225300)

先张法预应力混凝土结构因其构筑工艺较为简单，被广泛应用于相关工程中，先张法预应力混凝土简支空心板也在我国公路中、小桥工程中普遍使用。预应力空心板的典型病害为梁底纵向裂缝，其裂缝数量明显多于普通钢筋混凝土板，但裂缝成因目前尚未明确统一。

预应力筋和混凝土的界面黏结是先张法预应力体系的基础，一般认为界面黏结力由化学黏附力、摩擦力和机械咬合力等组成，受力筋直径、初始应力以及混凝土强度等因素影响。力筋放张后，混凝土自由端未立即形成有效应力，含有一段传递长度，在传递长度内混凝土纵向应力逐渐增大，力筋与混凝土相对滑移逐渐减少，最终形成稳定黏结。

对先张法预应力结构的试验研究较多，成果多为试验数据和经验公式[1-2]，试验研究的缺点一是受成本限制，难以建立全尺寸模型；二是受测量技术限制，不易获取全部数据。由于计算机技术的发展，近年来利用有限元方法对混凝土、预应力筋以及层间黏结建模取得一定成果[3-4]，我国《公路钢筋混凝土及预应力混凝土桥涵设计规范》(JTG 3362—2018)[5]也给出了弹性收缩和传递长度的计算公式。

先张法研究总体缺乏系统的力学理论与模型，对预应力的传递和形成以及局部应力分布等认识不足，有必要建立有效的力学模型对结构受力进行解析描述。基于厚壁圆筒理论，研究采用弹性力学方法对先张法预应力结构的应力损失、传递长度、滑移距离和应力应变分布等进行解析，推导出通用计算公式，并对不同计算方法进行比较。

1 厚壁圆筒模型

已有研究者尝试用厚壁圆筒理论分析先张法预应力，Benítez等[6]给出了预应力损失的解析解，Abdelatif等[3]演示了传递长度的部分推导，并用有限元方法证明了厚壁圆筒模型的适用性。但计算所需假定条件、变量定义、初始与终止状态的界定、滑移距离和应力分布计算以及解析解的数值实现等在相关文献中有所欠缺。为理清思路，方便复现和验证，本研究从弹性力学基本理论出发，明确假设条件与变量定义，逐步推演，给出应力损失、传递长度、滑移距离和应力应变分布的全部解析解。

厚壁圆筒模型如图1所示，预应力筋为内筒，外径由r1表示，内径由a表示(因预应力筋内部无孔隙，故a→0)；混凝土为外筒，外径由b表示，内径由r1表示，b取预应力筋最小覆盖层厚度处预应力筋中心到混凝土外表面的距离。因预应力筋内部无外力作用，故内径a处径向应力恒为0；因混凝土自由表面无正应力，故外径b处径向应力亦恒为0。界面r1处内外桶的径向应力都为-p(压应力)，由对称性可知剪应力τrθ=τθr=0。

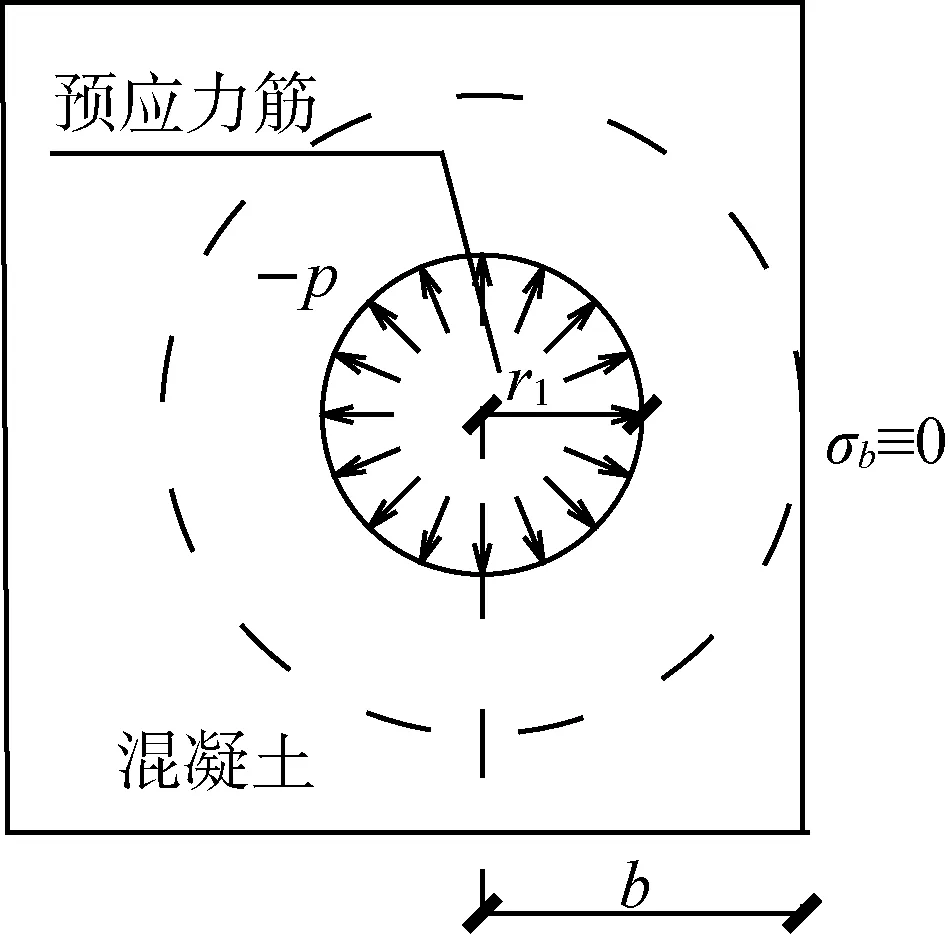
图1 厚壁圆筒模型

1.1 受力状态

放张前预应力筋和混凝土处于初始状态，放张后二者在外力作用下变形，并最终达到平衡状态。

1.1.1 初始状态

预应力筋截面积为As，半径为r1，纵向应力为0，半径a处径向应力为0。

混凝土截面积为Ac，纵向应力为0，半径b处径向应力为0。

1.1.2 平衡状态

预应力筋纵向应力σzs=-Δσ(z)，半径a处径向应力为0。

注意事项如下。

(1) 根据弹性力学小变形假设，计算时不考虑变形前后预应力筋、混凝土半径及截面积的变化，全部取初始状态值。

(2) 预应力筋初始半径r1为张拉后放张前的半径。

(3) 虽然预应力筋放张前有初始纵向应力σ0，但计算力筋放张后的变形时，只考虑变化量-Δσ，故初始应力取变化前的相对值0；而计算混凝土纵向应力时，需考虑初始应力σ0。

1.2 假定条件

用厚壁圆筒理论进行先张法预应力分析，应明确下列假定条件。

(3) 弹性力学基本假定[7]：物体连续、弹性、均匀且各向同性，位移和形变微小。

2 基本方程

系统为轴对称体系，三维应力如图2所示，坐标原点位于自由端的预应力筋圆心处，系统位于z轴正方向。

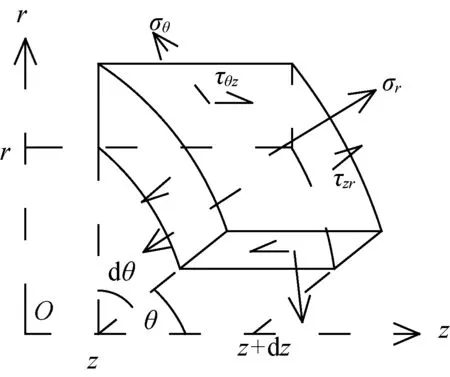
图2 三维应力

因体力为0，故径向平衡方程[7]如下：

(1)

几何方程[7]如式(2)和式(3)所示。

(2)

(3)

对式(3)求导，可得

(4)

物理方程[7]如式(5)和式(6)所示。

(5)

(6)

式中，E为杨氏模量；υ为泊松比。

由式(5)和式(6)可得

(7)

式(4)与式(7)联立可得

(8)

(9)

式(8)与式(9)联立可得

(10)

式(1)与式(10)联立可得

(11)

由式(1)可知

(12)

对式(12)求导，可得

(13)

式(13)代入式(11)可得

(14)

解微分方程式(14)，得到

(15)

式中，A和B为积分常数，可根据边界条件求得。

式(15)代入式(12)，得到

(16)

2.1 径向平衡

预应力筋和混凝土的径向受力如图3所示。

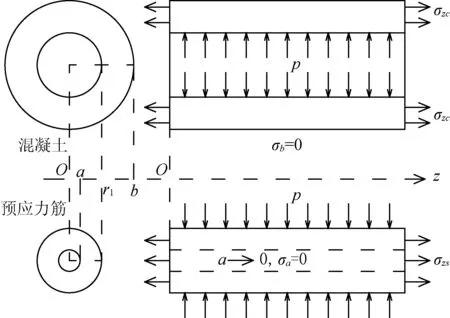
图3 预应力筋和混凝土的径向受力

对于预应力筋，利用边界条件σr|r=r1=-p，σr|r=a=0(a→0)，求得

(17)

对于混凝土，利用边界条件σr|r=b=0，σr|r=r1=-p，求得

(18)

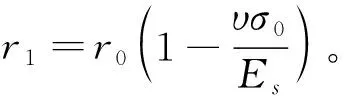
2.2 纵向平衡

预应力筋和混凝土的纵向受力如图4所示。

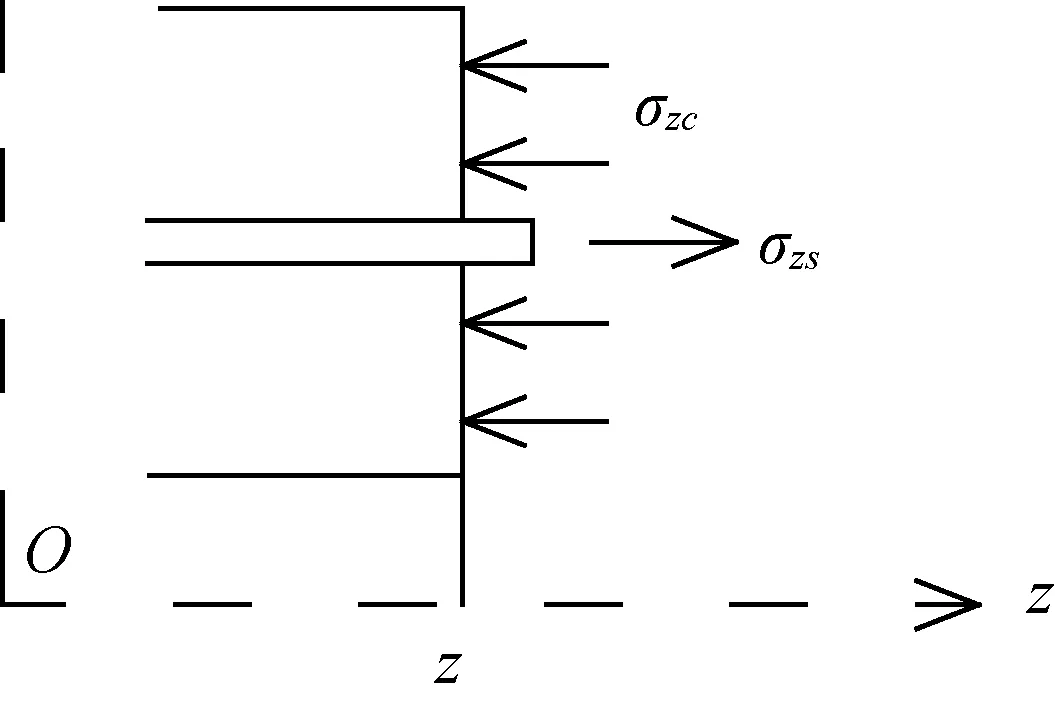
图4 预应力筋和混凝土的纵向受力

预应力筋内纵向应力放张前为σ0，放张后为σzs=σ0-Δσ(z)，混凝土内纵向应力放张前为0，放张后为σzc。则z处有纵向平衡方程：σzcAc+[σ0-Δσ(z)]As=0，解此得到

(19)

3 预应力损失

对于预应力筋，联立式(6)、式(15)、式(16)和式(17)，得到

(20)

(21)

(22)

对于混凝土，联立式(6)、式(15)、式(16)和式(18)，得到

(23)

(24)

(25)

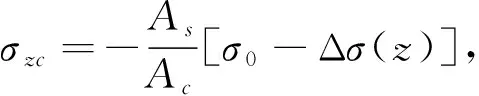
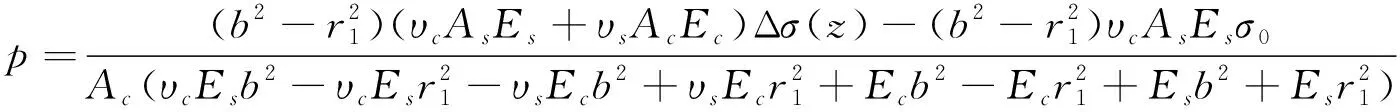
(26)

预应力筋纵向受力如图5所示。

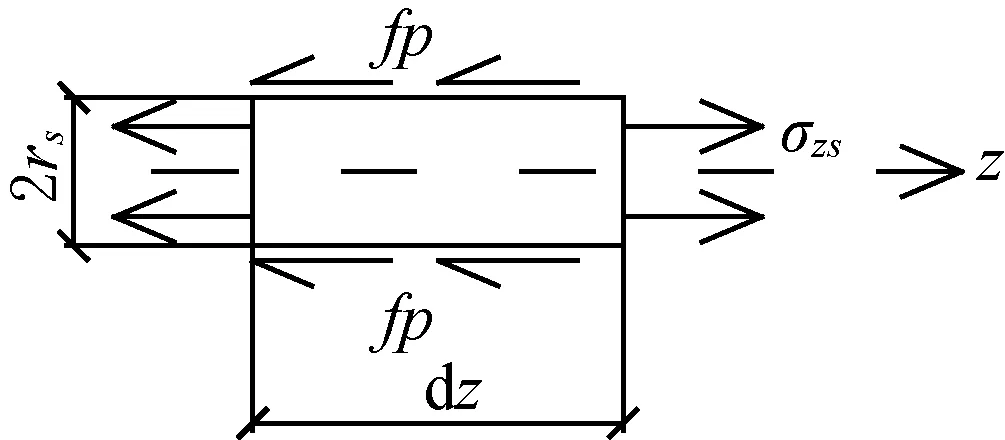
图5 预应力筋纵向受力

根据文献[3]和文献[6]，界面上的切应力主要和径向压应力有关，大致满足库仑定律τrz=f×p，f值通常为0.3～0.7，本文暂取0.4。

力筋纵向平衡方程为

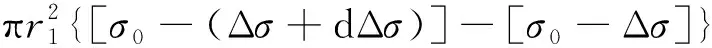
解此得到

(27)

(28)

式(28)为预应力损失计算式。

4 传递长度

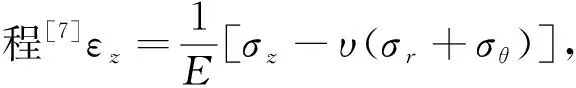
对式(28)求反函数得到

(29)

文献[3]认为可直接利用式(29)计算传递长度，即求解预应力筋Δσ=0.05σ0时对应的z值。

5 预应力筋滑移距离

取一微段构件dz，力筋与混凝土的相对滑移距离ds取决于二者的应变差：

ds=(εzs-εzc)dz

(30)

圆柱坐标纵向物理方程为[7]

(31)

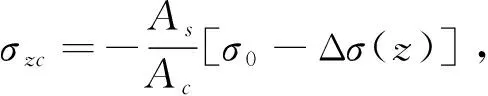
(32)

为方便计算，假定预应力筋与混凝土的相对滑动为一维应变问题，忽略径向和环向应力影响，则有

(33)

联立式(20)、式(21)、式(23)、式(24)、式(30)和式(33)，得到

(34)

联立式(28)和式(34)，并令

(35)

6 算例

6.1 传递长度计算

根据文献[2]取同样尺寸的试件和张拉力，计算预应力传递长度。试件参数如表1所示，试件截面尺寸如图6所示。

表1 试件参数

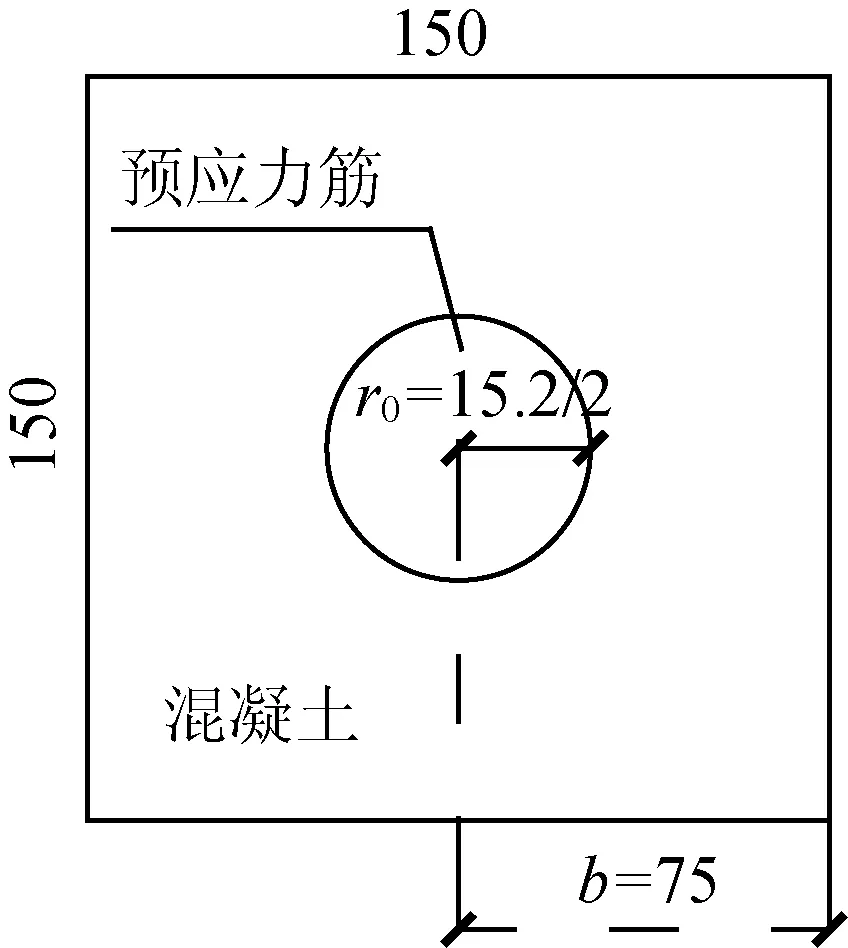
图6 试件截面尺寸(单位：mm)

分别计算混凝土95%纵向应变、钢绞线5%应力损失对应的传递长度，并与规范值和实测值进行比较，传递长度比较如表2所示。

表2 传递长度比较

计算结果表明，基于混凝土纵向应变和预应力筋纵向应力的传递长度计算结果差别较大，原因是按此模型计算时，跨中处钢绞线预应力损失不为0，致使按混凝土95%跨中纵向应变和按钢绞线5%应力损失计算的位置不一致。

此外还发现摩擦系数f对传递长度影响明显，C80混凝土在f取0.4时应变传递长度为625 mm，f取0.6时应变传递长度为416 mm。

解析解基于弹性力学假设，未考虑混凝土开裂和失效等情况，因此计算的传递长度与实测数据有差距，且与张拉力不相关。

6.2 空心板梁计算

以10 m空心板为例，采用Φs15.2钢绞线，混凝土标号C50，钢绞线距离底板外缘50 mm。在混凝土达到龄期7 d以上且设计强度90%以上后分批放松钢绞线。

空心板参数如表3所示。

表3 空心板参数

分别求得预应力损失、预应力传递长度、混凝土环向拉应力和混凝土纵向压应力的解析解，应力传递解析解如表4所示。其中εm为95%的跨中混凝土应变。

表4 应力传递解析解

接触面切应力分布如图7所示。

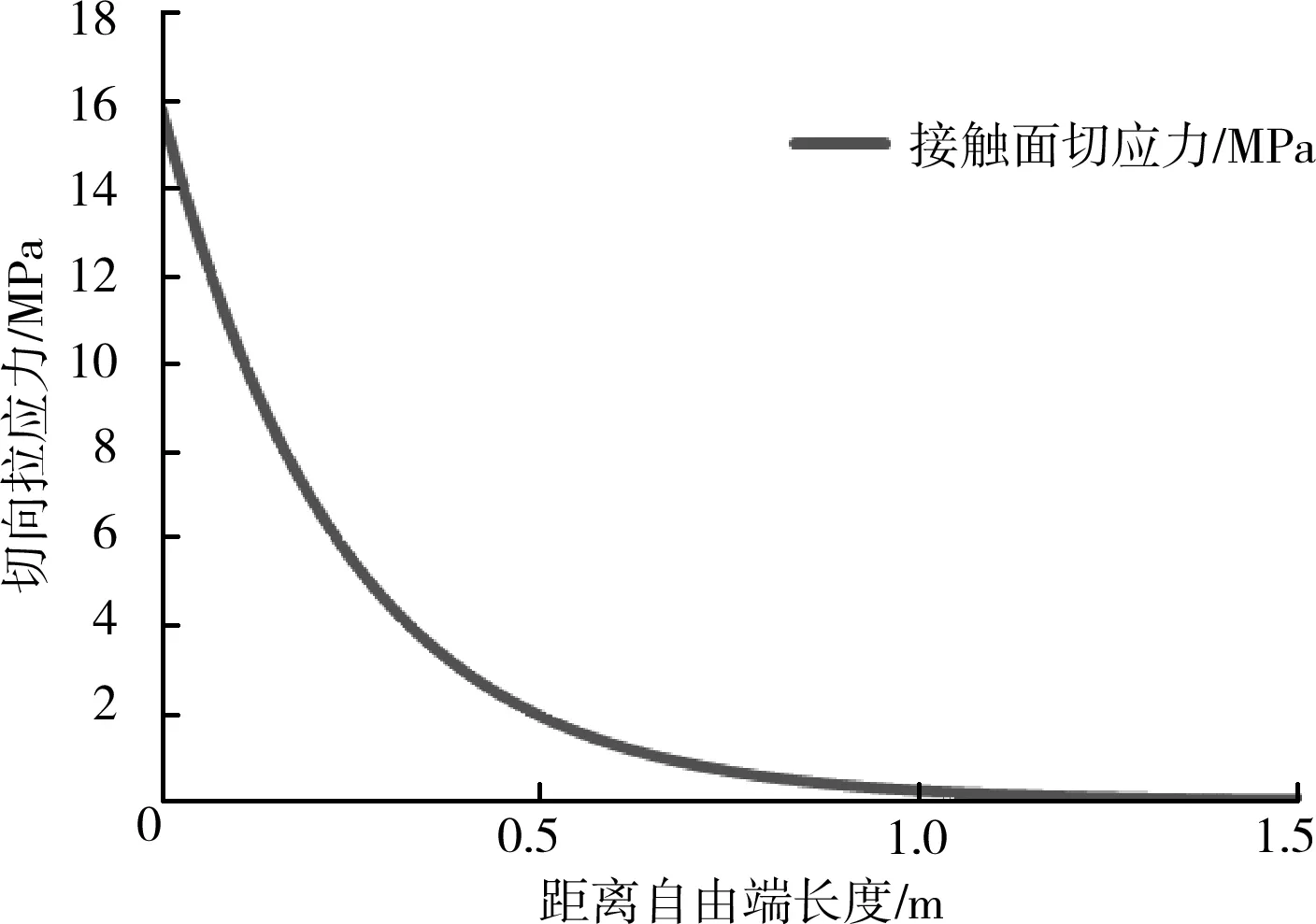
图7 接触面切应力分布

接触面附近混凝土应力分布如图8所示，接触面附近混凝土应变分布如图9所示。

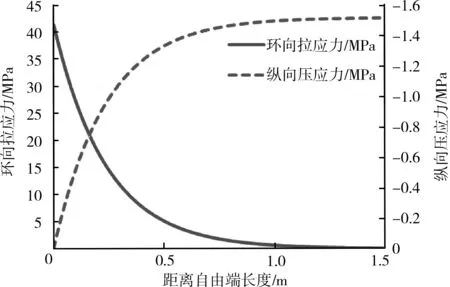
图8 接触面附近混凝土应力分布

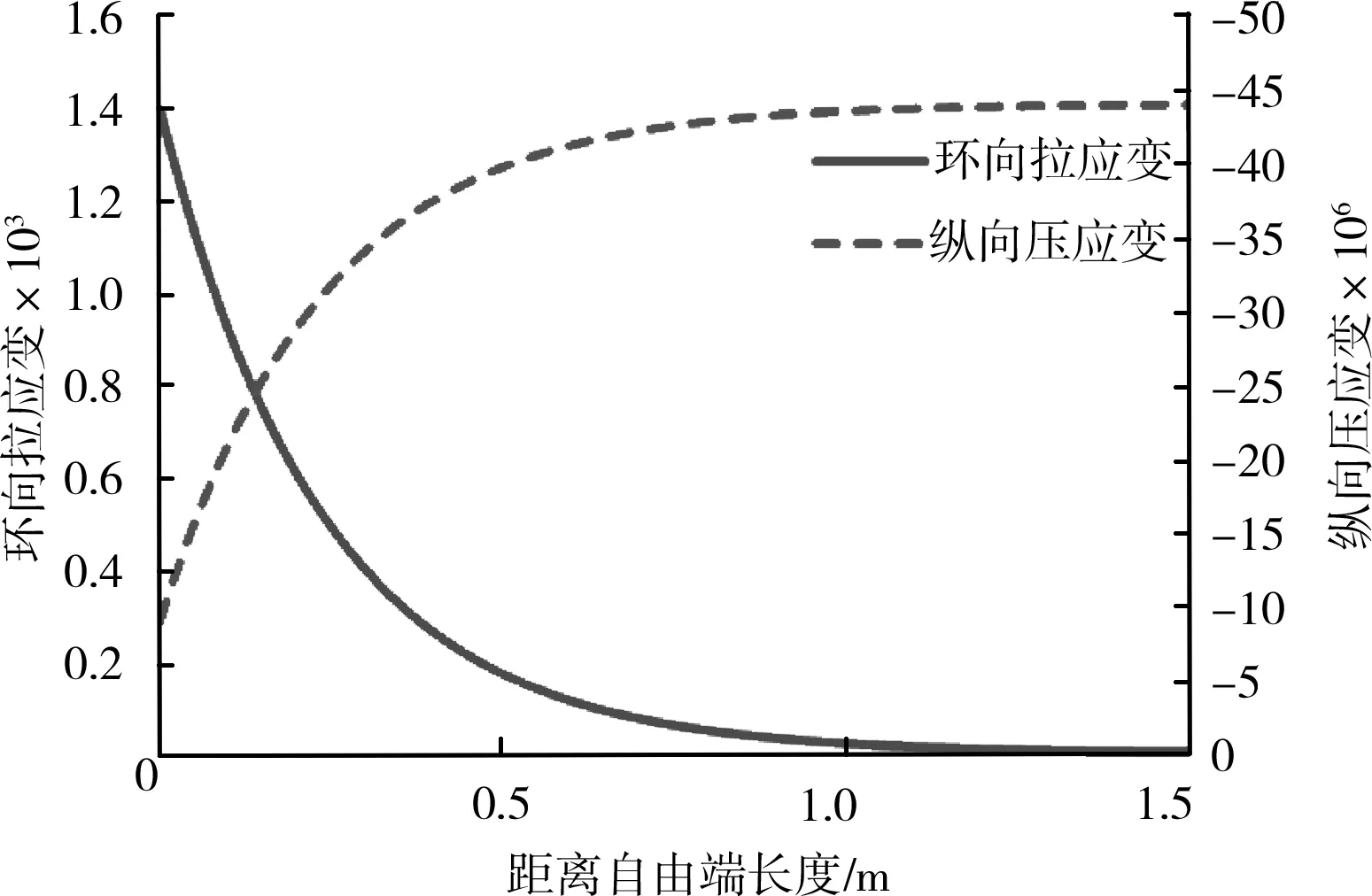
图9 接触面附近混凝土应变分布

可见端部环向拉应力和拉应变已远远超过混凝土抗拉强度和极限拉应变，如果不对该部位进行补强，混凝土开裂后握裹力降低，会导致初始裂缝沿纵向发展，影响结构安全性和耐久性。

分别用三向应力法和一维简化法计算预应力筋滑移距离，滑移距离计算如表5所示，数值解表明两者差别不大。

表5 滑移距离计算

预应力筋的应力损失和滑移距离如图10所示。

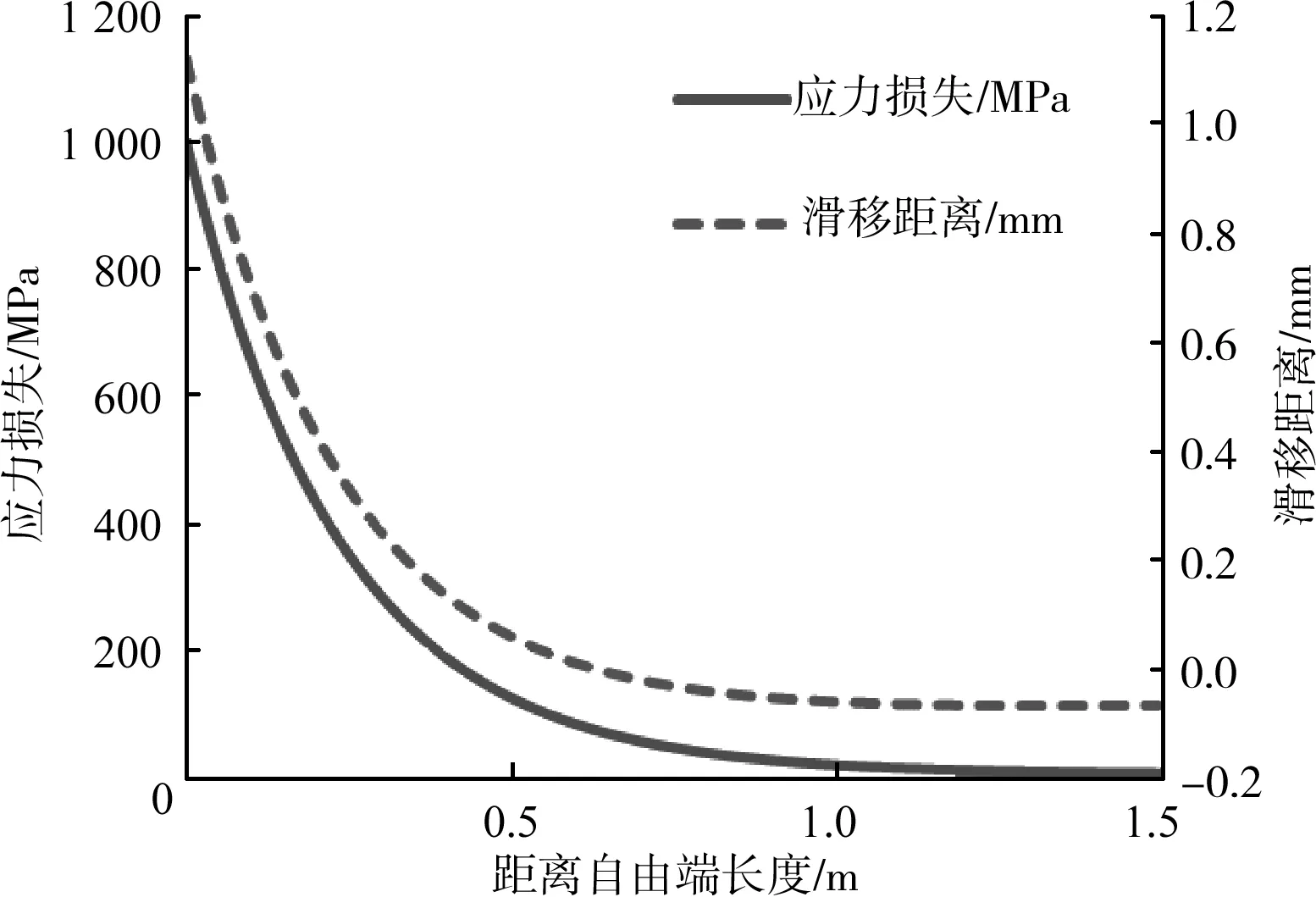
图10 预应力筋的应力损失和滑移距离

按相关规范和厚壁圆筒模型分别进行计算，应力损失、传递长度和滑移距离计算所得如表6所示。

表6 应力损失、传递长度和滑移距离计算所得

其中厚壁圆筒的应力损失值取Δσ|z=L/2。

7 结论

从弹性力学基础方程出发，基于厚壁圆筒模型，对先张法预应力混凝土结构的预应力传递、滑移和应力分布进行计算，逐步推导出应力损失、传递长度、滑移距离和应力应变分布公式，为先张法预应力研究提供理论工具。算例显示：①《公路钢筋混凝土及预应力混凝土桥涵设计规范》(JTG 3362—2018)中对应力损失和传递长度的计算比较保守；②预应力空心板的梁底纵向裂缝是由端部初始裂缝延伸形成的，预应力筋放张时，端部混凝土环向拉应力和拉应变明显超限，必须在该部位进行补强设计，防止混凝土失效导致裂缝纵向发展。