罗兰C与GNSS组合定位系统误差校正方法的研究
2022-01-21刘音华李孝辉刘长虹赵凡朱峰冯平
刘音华,李孝辉,刘长虹,赵凡,朱峰,冯平
罗兰C与GNSS组合定位系统误差校正方法的研究
刘音华1,2,李孝辉1,2,刘长虹1,赵凡1,2,朱峰1,冯平1
(1. 中国科学院 国家授时中心,西安 710600;2. 中国科学院大学,北京 100049)
GNSS(Global Navigation Satellite System)导航系统容易受电磁干扰,且易受遮挡,在复杂电磁环境和遮挡环境中的应用受限。罗兰C系统是陆基无线电导航系统,具有发射功率大、抗电磁干扰强等优势,可以把罗兰C发播台当作GNSS系统的伪卫星来进行组合定位,能大大提高导航系统的可用性和可靠性。本文从理论上分析了影响组合定位性能的因素,并提出了校正—融合的组合定位算法用以修正罗兰C系统误差,并基于实测数据研究分析了北斗和罗兰C组合定位性能。研究结果表明,基于蒲城罗兰发播台,在4~8颗可用卫星资源的情况下,采用本文提出的组合定位算法,可以达到数十米至百米量级的定位精度;北斗和罗兰C组合定位能大大优化几何精度因子;在北斗单系统GDOP值越大时,组合定位精度的改善程度也越大;在GDOP小于30的情况下,组合定位性能和北斗单系统相当。
全球卫星导航系统;Loran-C;组合定位;精度因子;系统误差校正
0 引言
GNSS(Global Navigation Satellite System)系统是目前业界公认的高精度的星基导航系统,但是基于GNSS系统的技术特征,它们在空间区段、运行与控制区段、用户区段都可能遭受敌方干扰[1-2]。此外,GNSS系统具有高频段、对大建筑物绕射能力差的特点,在大建筑物密集区域导航性能也会受到影响。因此,需要有其他导航系统进行辅助以提高GNSS系统的可用性和可靠性。罗兰C系统与GNSS系统的技术特征正好互补,罗兰C信号具有很强的抗干扰能力和对大建筑物的高绕射能力,正好弥补了GNSS系统的不足。罗兰与GNSS组合定位的优势体现在GNSS系统受到干扰和多遮挡环境下,罗兰发播台可以当作GNSS系统的伪卫星,有效改善系统的DOP(dilution of precision)值,提升系统的可用性和可靠性[3-5]。近年来,许多国家都在大力升级罗兰系统,把罗兰C系统升级为eLoran系统,也在建设差分罗兰系统,更好地为GNSS系统提供辅助增强。中国也在朝这方面努力,目前基于实测数据的研究大多都基于罗兰C系统,为罗兰C系统的升级改造提供技术支撑和积累。
但是罗兰C系统定位误差在百米量级[6-8],传统认为罗兰C系统不能与GNSS系统进行组合定位,否则会降低GNSS系统原有的定位性能。罗兰C系统定位误差主要包括AF、SF和ASF修正误差、发射和接收设备时延标定误差、罗兰C信号传播路径建模误差等等,这些都属于系统误差。因此,需要采取有效的方法对罗兰C系统进行系统误差校正,才能实现较好的双系统组合定位精度,从而充分利用罗兰C系统的优势来弥补GNSS系统的一些缺陷[9-11],增强GNSS系统的可用性和可靠性。
本文在分析罗兰C与GNSS系统组合定位原理的基础上,对影响组合定位精度的原因进行了分析。提出校正—融合的组合定位算法用以修正罗兰C系统误差。然后,采集北斗接收机和罗兰C接收机的实测数据进行组合定位解算,基于实际数据研究北斗和罗兰C组合定位性能。此外,基于同一时段数据分析了北斗单系统定位结果,对比研究组合定位和北斗单系统定位效果。最后,还对比研究了北斗和罗兰C组合定位对几何精度因子的改善情况。
1 影响组合定位性能的因素分析
以3颗GNSS卫星和一个罗兰C发播台进行组合定位为例来研究组合定位数学模型。组合定位伪距观测方程如式(1)所示。



图1 组合定位影响因素
罗兰C系统影响组合定位的误差主要包括PF、SF和ASF修正误差、发射和接收设备时延标定误差、罗兰C信号传播路径建模误差和接收机噪声等等。PF是一次相位因子修正误差,主要由信号在真空和在空气中传播速度差造成的,可以通过公式进行修正[16]。SF是二次相位因子修正误差,主要由信号在海水和空气中的传播速度差造成,也可以通过公式计算[16]。ASF附加二次相位因子的影响是主要误差源[17],为实际陆地下的时延与全海水路径下的时延偏差。很多文献表明可以通过查表法进行修正,表格的制定需要GPS定位接收机或其他定位设备进行事先标定,这样既费时费力,也会因为采样点的选取间隔导致修正精度降低。发射和接收设备时延可以标校,但需要购买昂贵的仪器设备才能进行高精度的标校,在普通民用设备中一般不进行设备时延的标校。罗兰C信号传播路径是采用椭球面进行建模的,但是地球并不是标准的椭球体,因此必然会引入建模误差。在实际应用过程中,PF和SF公式修正后的残余误差、传播路径建模误差会被组合起来,在ASF标定时统一修正,整体修正精度在微秒量级。
因此,影响组合定位精度的主要原因是与罗兰C系统相关的误差,单GNSS系统定位精度已经很高,普通伪码型接收机均能达到十米甚至米级的定位精度,如果不采取合适的方法对罗兰C观测数据进行误差修正,则会恶化组合定位性能。
PF、SF和ASF修正误差、发射和接收设备时延标定误差、罗兰C信号传播路径建模误差等都属于系统误差,系统误差具有重复性和可测量性。而且,罗兰C地波传播时延具有较好的稳定性。因此,只要找到合适的方法,就能对这些系统误差进行统一修正,这也是本文的研究重点。
2 罗兰C系统误差校正
既然是进行罗兰C与GNSS的组合定位,因此可以利用GNSS系统较高的定位精度来标校罗兰C系统的系统误差,然后再进行双系统的组合定位。本文提出校正—融合的方法来进行罗兰C系统误差的校正,采用GNSS接收机来标校罗兰C系统的系统误差,然后再进行两个导航系统数据的融合处理,得到组合定位结果。组合定位的具体工作流程如图2所示。整个组合定位解算分为两个主要过程。一个是利用GNSS接收机进行待测点的坐标预标校的过程,也是所谓的校准过程。在校正时采用GNSS单系统进行一段时间的定位,获得GNSS单系统定位结果,用该结果来修正罗兰C数据的系统误差。另一个是罗兰C系统和GNSS双系统数据融合定位解算的过程,扣除系统误差的观测数据与北斗观测数据融合,进行组合定位。组合定位坐标的求解过程是与单GNSS系统坐标求解过程类似,是一个迭代过程,直到满足一定的收敛条件。
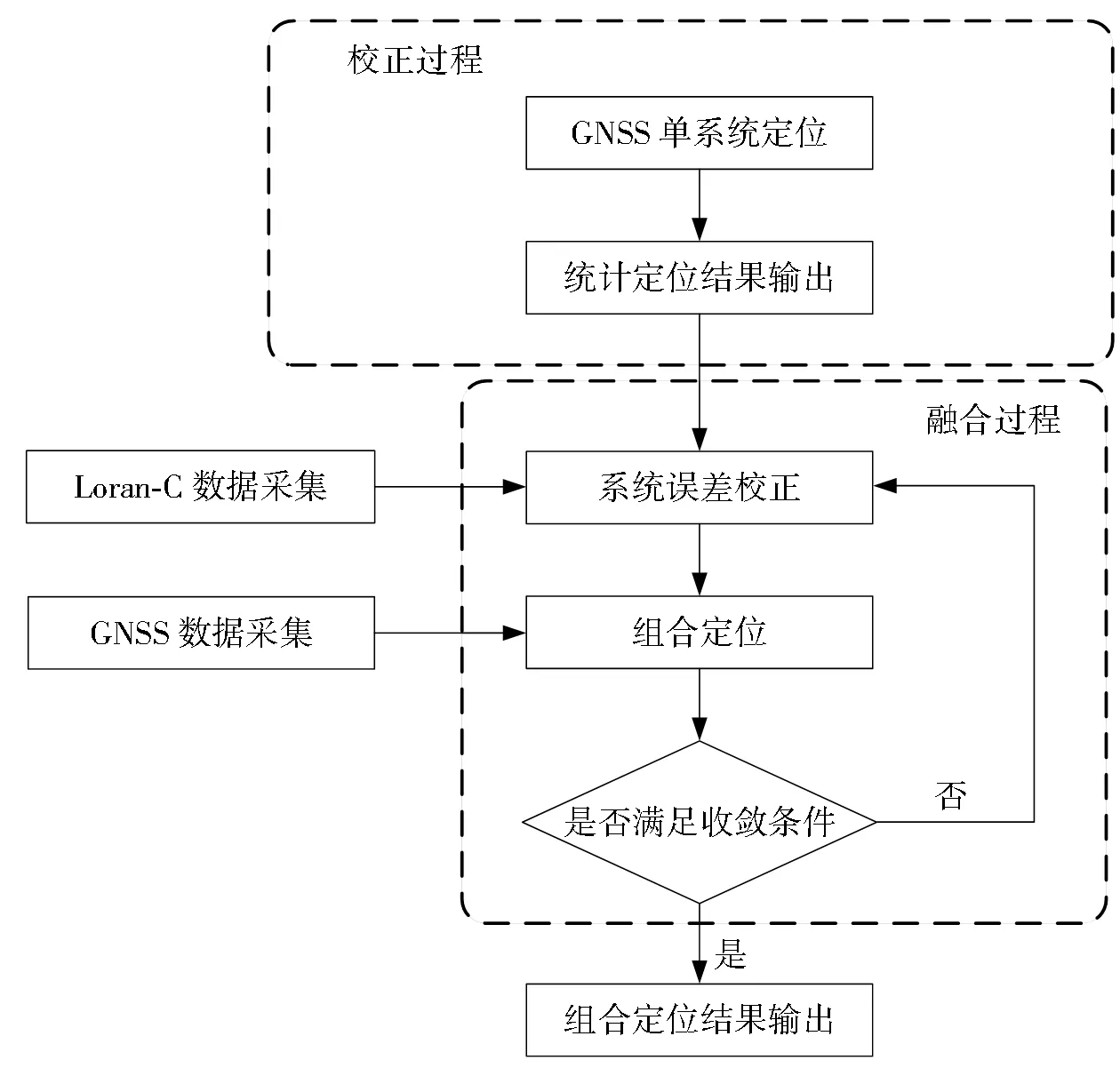
图2 组合定位工作流程
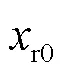



从上述系统误差的修正方法可知,在进行系统误差的修正时并不区分是哪一种系统误差,而是把所有的系统误差进行打包处理,统一修正。

图3 系统误差迭代校正过程
3 组合定位性能分析
本文基于西安临潼北斗接收机和罗兰C接收机接收蒲城罗兰C发播台的实测数据进行组合定位实验数据处理与分析,首先就双系统组合定位对几何精度因子的改善情况进行研究,然后进行双系统组合定位实验,分析组合定位性能,并与北斗单系统定位性能进行对比。
为了方便下文进行描述,对本文具体开展的实验项目进行编号,见表1所示。编号为S1至S7的实验为北斗单系统定位实验,字母S表示北斗单系统定位分析;编号为I1至I7的实验为双系统组合定位实验,字母I表示组合定位分析。表1中,1~5号星为GEO卫星,6、8、9号星为IGSO卫星。实验数据时长为1 h,数据间隔为1 s,组合定位时前半小时的数据用于校正系统误差,后半小时的数据用于评估组合定位效果。
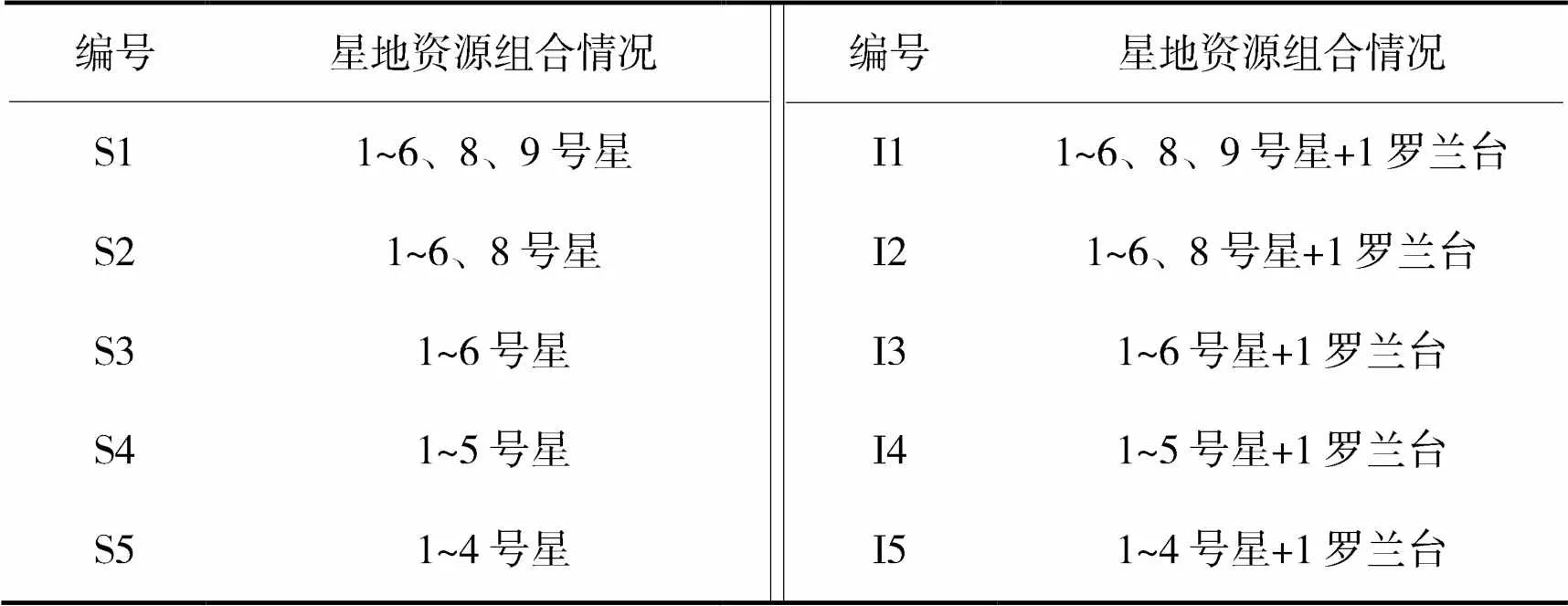
表1 组合定位实验项目编号与星地资源对应关系

续表1
3.1 几何精度因子分析
卫星导航系统的定位精度一方面由用户等效距离误差(UERE)决定,另一方面由卫星星座的几何布局决定,几何精度因子(geometric dilution of precision,GDOP)是衡量卫星星座几何布局优劣的一个物理量[8-9]。因此,本文比较了组合定位和北斗单系统定位的几何精度因子,表2为临潼GDOP、PDOP(position dilution of precision)和TDOP(time dilution of precision)的计算结果,表中的各个实验编号与表1对应。

表2 几何精度因子分析
从表2可以看出,北斗和罗兰C组合定位能优化几何精度因子,各项DOP值较北斗单系统均大大减少。将表2中组合定位DOP值相对于北斗单系统DOP值的改善量换算为百分比,得到相应的改善程度,如表2中“改善程度”列所示。从改善程度可以看出,组合定位对几何精度因子(GDOP)、位置精度因子(PDOP)和时间精度因子(TDOP)均有大程度的改善,最大的改善程度达到80%,最小的改善程度也有37%。从表2可以进一步发现,在北斗单系统DOP值越大时,双系统组合DOP值的改善程度相对来说也较大,对位置精度因子(PDOP)和时间精度因子(TDOP)均是如此。由此可见,引入一个罗兰C地面发播台,可以大大改善星座的几何精度因子,对于星座几何分布本身欠佳的情况,改善尤为突出。
3.2 组合定位效果分析
采集北斗接收机的双频伪码观测量和罗兰接收机的观测数据,按照表1的实验项目分别进行双系统组合定位和北斗单系统定位解算,分析定位误差。
图4(a)为实验项目I1的定位误差图,为8颗北斗卫星和蒲城罗兰发播台组合定位结果。从图上可知,1~6、8、9号星和蒲城罗兰发播台组合定位误差小于20 m。图4(b)为实验S1的定位误差图,仅为北斗单系统的定位结果,定位误差也小于20 m,与双系统组合定位精度相当。各个维度的定位误差统计结果见表3所示,组合定位在轴上大约有3 m的定位精度改善;但在轴上,组合定位性能有所恶化,定位误差大约增加了2.4 m;总的位置误差方面,组合定位和北斗单系统相差不大,仅为0.3 m。
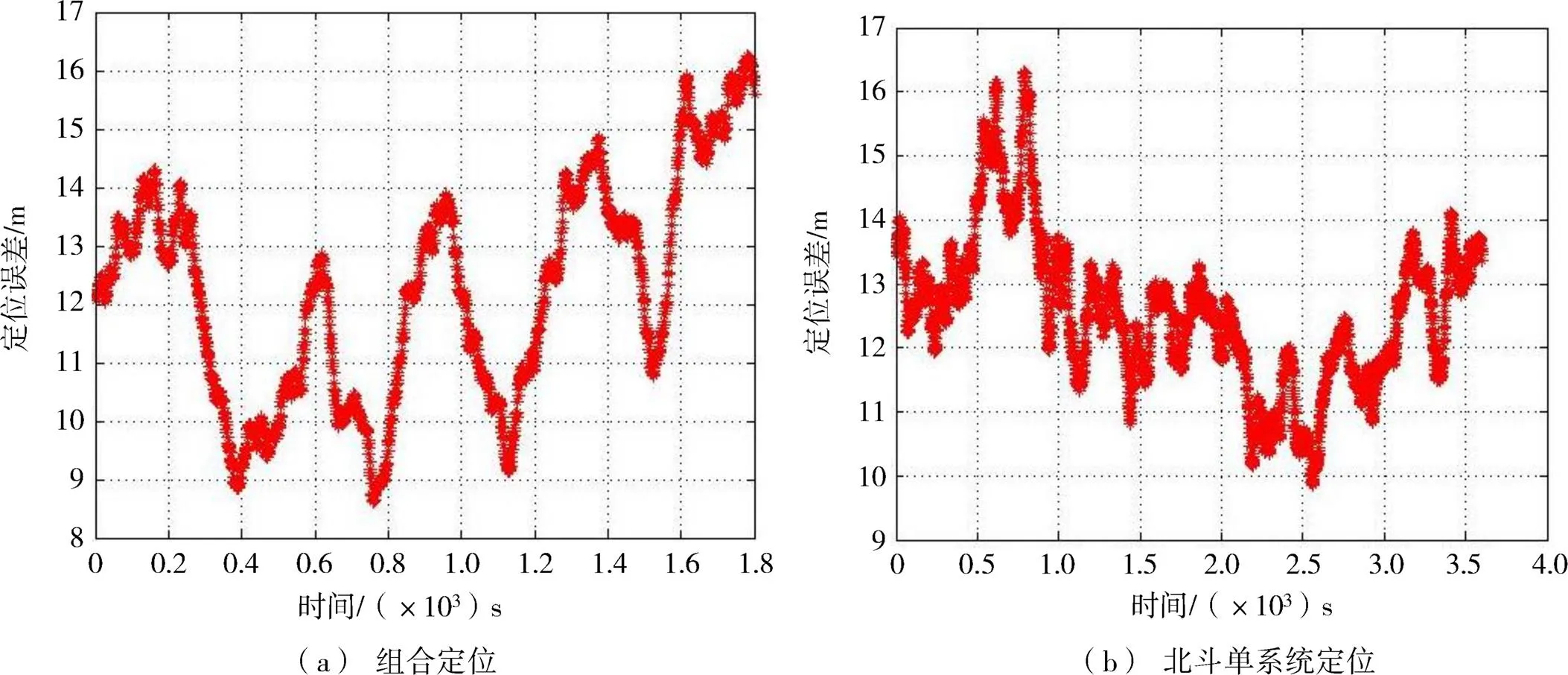
图4 实验I1与S1定位误差对比
图5(a)和(b)分别为实验项目I2和S2的定位误差图,在图4实验的基础上去掉了9号星。从图5可知,1~6、8号星和蒲城罗兰发播台组合定位误差也在20 m以内,与北斗单系统的定位精度大致相当。从表3定位误差统计结果可以看出,在轴和轴上,组合定位误差均小于北斗单系统定位,总的定位误差减少了1.8 m。粗略对比图4和图5,发现在去掉了9号星的情况下,不论是组合定位还是北斗单系统定位,定位精度并没有明显的恶化。经过分析发现,一方面是由于9号星在此数据时段高度角偏低,观测数据质量有所下降。另一方面是因为9号星对几何精度因子的改善并不明显,表2的DOP值分析结果即可说明,去掉9号星前后的DOP值相差不大。

图5 实验I2与S2定位误差对比
图6(a)和(b)分别为实验项目I6和S6的定位误差图,采用了1~3号星和8号星的观测数据。从图6可知,此时,组合定位误差在30m以内,与北斗单系统的定位精度大致相当。结合表3定位误差统计结果可知,在轴、轴和轴上,组合定位误差均小于北斗单系统定位,总的定位精度提升了2.7m。结合表2的TOP值分析结果,发现1~3号星和8号星组合时的DOP值明显优于其他8号星缺失的情况,即使可用卫星数目更多。可见,在此时的观测时段内,8号星是北斗系统的一颗关键卫星,对良好的星座几何结构构建至关重要。
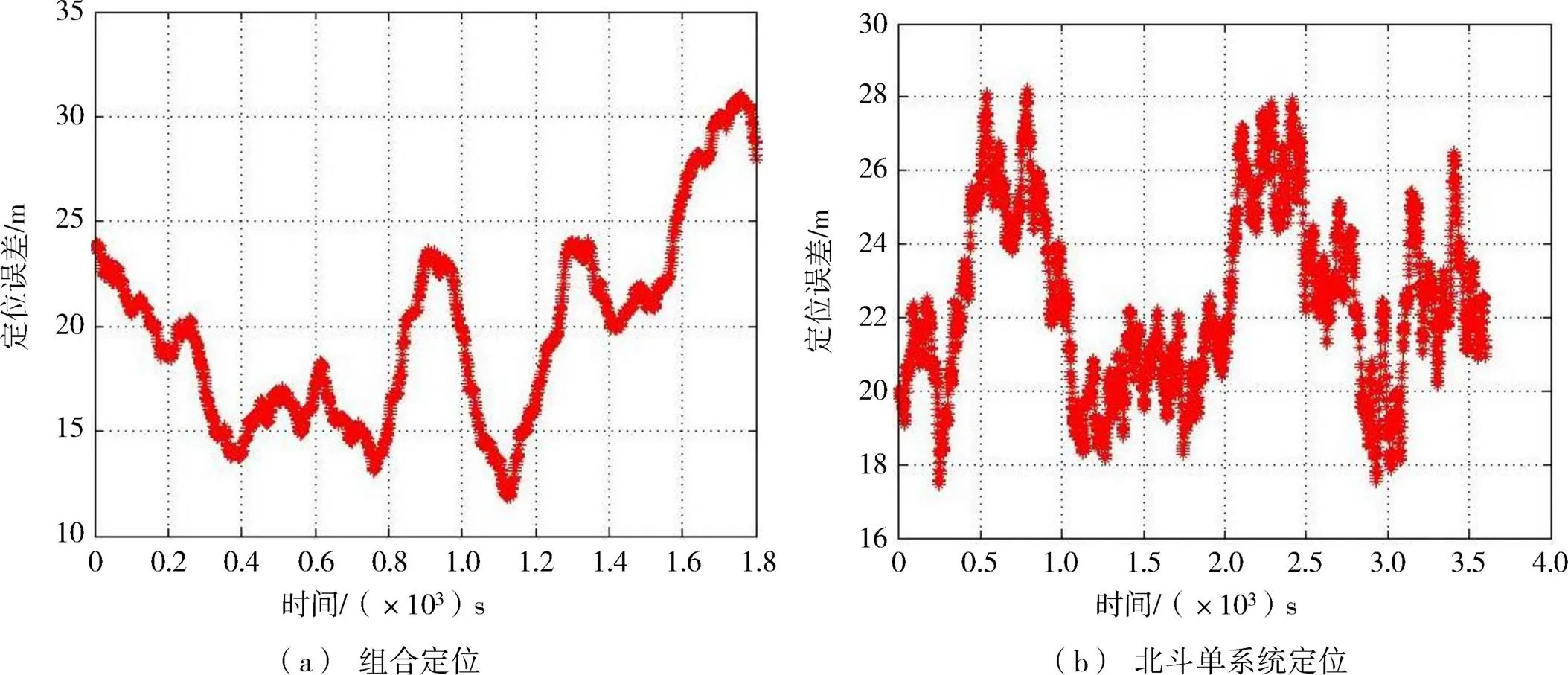
图6 实验I6与S6定位误差对比
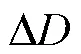
结合表3的统计数据可知,在现有蒲城罗兰发播台资源的基础上采用本文提出的校正—融合算法可以达到数十米至百米量级的组合定位精度。实验4和实验5定位精度最低,组合定位与北斗单系统定位的定位误差统计值均在百米量级。这是由于这两个实验几何精度因子较高,北斗单系统的PDOP值在60以上,组合定位的PDOP值也在10以上。除了实验3与实验7,组合定位均能减少一定程度的定位误差,实验4和实验5定位精度提升最多,达到20~30 m。实验3与实验7,尽管组合定位的几何精度因子较北斗单系统有较大优化,但北斗单系统本身的定位精度在20~30 m范围,而罗兰C观测数据本身的随机噪声也在几十纳秒量级,如果不对罗兰观测数据进行降噪预处理,组合定位性能可提升的空间并不大。
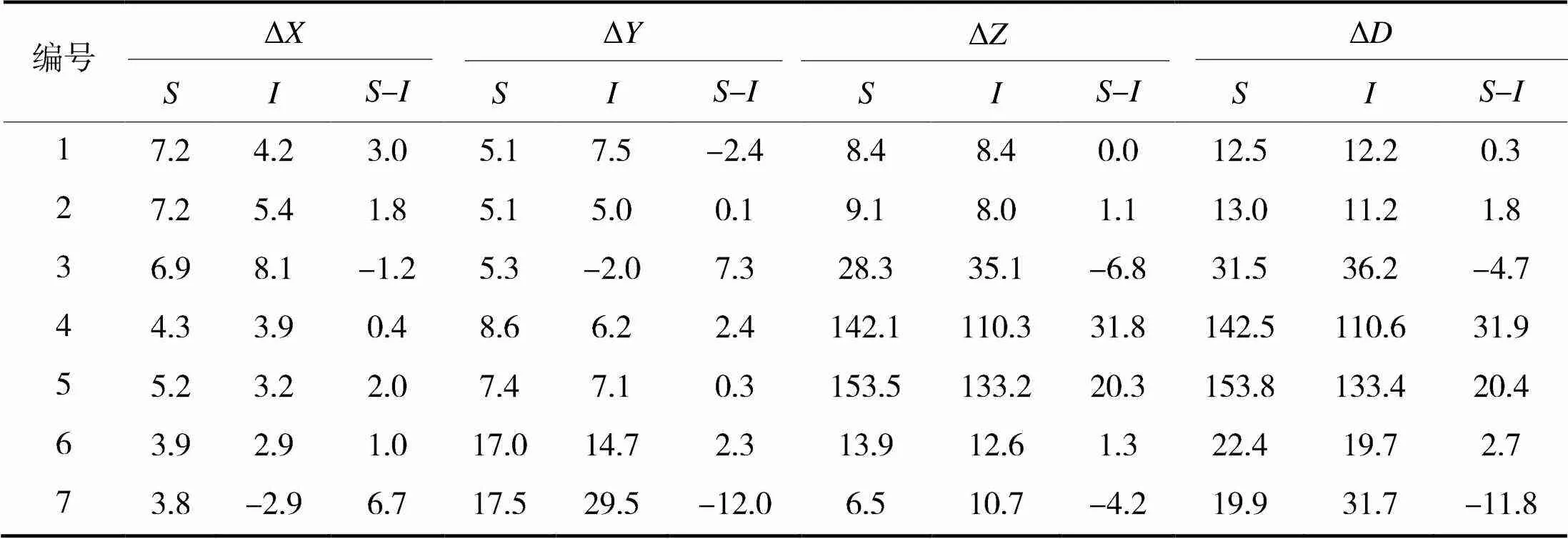
表3 组合定位与北斗单系统定位误差对比 单位:m
从各个维度定位误差的统计结果可以大致看出,不论是组合定位和北斗单系统定位,方向的定位误差所占的比重大于和方向,方向的定位误差在数米至百米量级范围内。和方向的定位误差均在十米量级的范围之内。
综合表3和表2,在北斗系统GDOP值30以下时,组合定位和北斗单系统定位精度相当,定位误差都在十米量级。当北斗单系统GDOP值急剧恶化时,例如实验4和实验5,GDOP值到了60以上,此时罗兰C与北斗组合定位性能更优。尽管组合定位能够带来几何布局的改善,但罗兰C信号传播的随机误差较大,即使对系统误差进行了校正,在罗兰C信号残余误差的影响量大于几何布局的改善量时,组合定位的性能得不到提升,例如实验1至实验3。当几何布局的改善量大于罗兰C信号残余误差的影响量时,组合定位的性能可以得到提升,例如实验4和实验5。
4 结语
分析结果表明影响罗兰C与GNSS组合定位性能的主要因素是罗兰C系统误差,提出校正—融合的组合定位算法来修正罗兰C系统误差。基于实测数据验证了所提方法的有效性,并与北斗单系统定位进行对比。基于实际研究结果,得到以下结论:
① 以蒲城罗兰C发播台和北斗系统进行组合定位,在4~8颗可用卫星资源的情况下,采用本文提出的算法可以达到数十米至百米量级的定位精度;
② 北斗和罗兰C组合定位能大大优化几何精度因子,包括PDOP和TDOP;
③ 在北斗单系统GDOP值越大时,组合定位精度的改善程度越大。在GDOP小于30的情况下,组合定位不一定能改善定位精度,定位性能和北斗单系统相当;当北斗单系统GDOP值急剧恶化至60时,组合定位性能更优。
[1] 李实锋. 罗兰-C数字化定时接收机关键技术研究[D]. 北京: 中国科学院研究生院, 2009.
[2] 张戎, 路明, 龚涛, 等. 复杂电磁环境下罗兰C系统作为GPS备份的探讨[J]. 全球定位系统, 2010(4): 43-46.
[3] 王森, 朱筱虹, 朱小辉, 等. 国外卫星导航系统的最新发展与思考[J]. 全球定位系统, 2015, 40(4): 61-64.
[4] 张风国, 欧明, 刘钝, 等. 未来潜在PNT技术综述[J]. 全球定位系统, 2015, 40(6): 27-34.
[5] WARD N, HARGREAVES C, WILLIAMS P, et al.Delivering resilient PNT[C] // 2015 International Association of Institutes of Navigation World Congress, Prague: IEEE, 2015.
[6] 曹可劲, 朱银兵, 张磊, 等. 罗兰C双台链交叉定位算法研究[J]. 海军工程大学学报, 2011, 23(3): 1-4.
[7] 华宇, 郭伟, 燕保荣, 等. 我国授时服务体系发展现状分析[J]. 时间频率学报, 2016, 39(3): 193-201.
[8] 严建华.罗兰C授时监测技术研究[J]. 现代导航, 2013(5): 331-337.
[9] 刘辛涛, 胡安平.长波导航系统拓展应用研究[J]. 现代导航, 2013(2): 116-119.
[10] 马敏.eLoran: 未来卫星导航的备份[J]. 中国海事, 2015(11): 54-56.
[11] 佟海鹏, 徐海刚, 刘兆平.复杂环境下罗兰C/北斗组合定位系统GDOP仿真分析[J]. 舰船科学技术, 2012, 34(5): 108-112.
[12] 丁晓光. 对流层延迟改正在GPS数据处理中的应用与研究[D]. 西安: 长安大学, 2009.
[13] 武文俊, 李志刚, 李孝辉, 等.IGS电离层产品在双向时间频率传递中的应用[J]. 宇航计测技术, 2012, 8(4): 51-54.
[14] LIU Y H, LI X H, ZHANG H J, et al.Calculation and accuracy evaluation of TGD from IFB for BDS[J]. GPS Solutions, 2016(20): 461-471.
[15] ZHANG Q, ZHAO Q L, ZHANG H P, et al.BDS Satellites and Receivers DCB Resolution[C] // Proceedings of the 5th China Satellite Navigation Conference, Nanjing: [s.n.], 2014: 187-197.
[16] SONG S P, CHOI H H, KIM Y B, et al.Verification of GPS Aided Error compensation method for eLoran using raw TOA measurements[C] // 2011 11th International Conference on Control, Automation and Systems, Korea: [s.n.], 2011.
[17] 杨光, 欧阳光洲, 郝巍娜, 等.CAPS/罗兰C组合定位系统的DOP值研究[C]//第四届中国卫星导航学术年会电子文集, 武汉: 第四届中国卫星导航学术年会组委会, 2013.
The study of systematic error calibration method for Loran-C and GNSS integrated positioning
LIU Yin-hua1,2, LI Xiao-hui1,2, LIU Chang-hong1, ZHAO Fan1,2, ZHU Feng1, FENG Ping1
(1. National Time Service Center, Chinese Academy of Sciences, Xi’an 710600, China;2. University of Chinese Academy of Sciences, Beijing 100049, China)
The application of Global Navigation Satellite System (GNSS) is limited in some complicated electromagnetism environment as it may be disturbed and blocked off easily. Long Range Navigation System (Loran-C) is a kind of terrestrial radio navigation system, which has the advantages of great transmitting power and strong ability of anti electromagnetic interference. Loran-C terrestrial transmitting station can be considered as a pseudo-satellite. Thus, GNSS and Loran-C can be integrated to realize positioning, it can improve the performance of navigation systems in complicated electromagnetism environment and also can realize positioning in single system blind area. In this study, the influence factors of integrated positioning were analyzed firstly, and the positioning algorithm based on calibration and fusion was presented to correct the systematic error of Loran-C data. Then, the performance of integrated positioning was analyzed based on the data collected from Beidou Navigation Satellite System (BDS) and Loran-C receivers. The positioning result of integrated systems was compared with the single BDS. Finally, the effect of integrated systems on geometric dilution of precision (GDOP) was studied. The results shown that based on the Pucheng Loran station, the positioning accuracy of tens or hundreds of meters can be achieved while used the proposed integration algorithm. The GDOP was improved greatly by the BDS and Loran-C systems integration; the improving effect of positioning accuracy was more obvious while the value of GDOP was greater, the performance of integrated positioning was in the same order of magnitude as BDS positioning while the GDOP value was smaller than 30.
Global Navigation Satellite System (GNSS); Loran-C; integrated positioning; dilution of precision (DOP); systematic error calibration
10.13875/j.issn.1674-0637.2021-04-0322-09
刘音华, 李孝辉, 刘长虹, 等. 罗兰C与GNSS组合定位系统误差校正方法的研究[J]. 时间频率学报, 2021, 44(4): 322-330.
2021-05-21;
2021-07-28
“十三五”国家重大科技基础设施资助项目(2018777)
