长期车辆荷载作用下软基路堤沉降预测研究
2022-01-21李海敏
李海敏
(广东粤路勘察设计有限公司, 广东 广州 510630)
0 前言
随着平原地区公路建设密度不断加大,目前拟建公路大多位于地质条件复杂的山地地区,呈多斜坡和软弱土层分布,此类公路在长期车辆荷载作用下,路基所形成的沉降难以预测,因此掌握其在长期车辆荷载下的沉降规律具有十分重要的意义[1]。为实现在地质、载荷等多种因素共同影响下的路基沉降预测,专家学者对此展开了深入研究。刘寒冰等[2]针对传统灰色模型的背景值误差,提出了采用非齐次指数拟合重构背景值的方法,并得到改进后的MGM(1,3)模型比传统GM(1,1)模型预测精度更高的结论;李亚峰等[3]通过自适应搜索算法分析了预测值与实测值之间的关系准则,验证了沉降预测模型的有效性;郑罗春[4]依托LSTM网络预测模型容错性高、记忆力强等特点,建立了高速公路路基长期沉降的时序化模型,并与指数曲线法预测值进行对比,证明了LSTM网络模型的准确性;洪英维[5]以某高速软土路基为例,探讨了双曲线模型、星野法模型等预测模型的路基沉降预测数据,并与实测值进行对比,得到软土路基沉降速率的波动规律。
综上所述,专家学者的研究侧重于采用不同方法实现对路基沉降的预测,但对于软基路堤在车辆荷载下的沉降趋势较少关注,基于此,本文提出一种新型的路基沉降预测模型,其基本原理是采用智能优化算法对支持向量机进行改进,通过对有限元数值计算结果的学习训练,完成车辆荷载下软基路堤的长期沉降预测。
1 有限元计算模型
某公路为双向四车道,线路斜穿山体鞍部,斜穿段地基左低右高,采取半挖半填形式。软基路堤自下而上分为地基层、软土层和路堤层3部分,软土层厚8 m,地层横断面如图1所示。几何模型宽为100 m,路堤中心线填土高4.0 m,路面宽40 m。为简化有限元软件计算的同时保证数值模型计算的收敛性和精确性,地基采用整体模拟方式,各土层均视为均质材料,考虑不规则模型分网的合理性,路面及下部土体均采用四面体实体单元,假设路堤与地基连续,对模型底部施加完全固定约束,并对模型四周分别施加法向约束,即仅考虑土体四周边界的沉降变形,不考虑侧向位移情况。有限元模型网格划分如图2所示,各土层材料的参数如表1所示。

图1 地层横断面示意图(单位: m)

图2 有限元模型
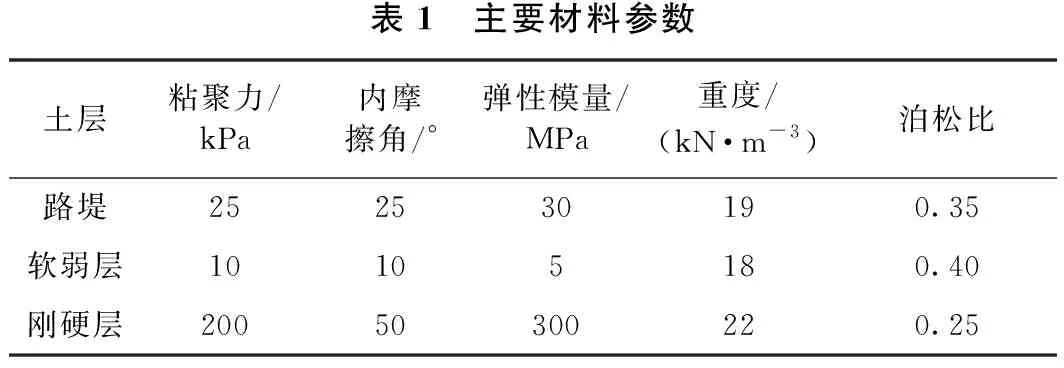
表1 主要材料参数土层粘聚力/kPa内摩擦角/°弹性模量/MPa重度/(kN·m-3)泊松比路堤252530190.35软弱层10105180.40刚硬层20050300220.25
与普通动力荷载不同,车辆荷载具备频率高、周期短等动态特点,不同车辆的荷载大小、车轮-路面耦合振动的存在使得路基受力特性极为复杂。本文采用幅值加载形式实现对车辆荷载的模拟,在路面设置2条加载带,取车速60 km/h,轴载分别125 kN为荷载工况加载7 500次进行计算。
2 基于PSO-LSSVM的路基沉降预测
2.1 最小二乘支持向量机原理
支持向量机(SVM)本质是一种基于统计方法的机器学习算法,通过输入向量从低维特征空间向高维特征空间的映射缩小样本误差,提高模型泛化能力。根据优化问题的特点,支持向量机采用对偶形式转化目标函数,其基本对偶形式如式(1)所示:
(1)
式中:α为拉格朗日乘子;x、y分别为数据集在特征空间上的坐标;K为非线性映射的核函数。
最小二乘支持向量机(Least Square Support Vector Machine,LSSVM)是在原始支持向量机中引入最小二乘的一种改进方式,其基本原理是对优化目标进行改造,采用等式约束与误差平方损失函数构建新的数学模型[6],提高计算效率。LSSVM的优化函数如式(2)所示:
式中:ω为权向量;e为松弛因子;γ为惩罚系数;b为待定参数。
对上述最优数学模型进行求解后,即可求得最小二乘向量机的回归函数,如式(3)所示:
(3)
2.2 基于粒子群算法的核参数优化
粒子群优化算法(PSO)是一种基于仿生学原理的智能群优化算法,其基本原理为利用粒子之间的信息共享不断对粒子的速度与位置进行迭代更新,直到粒子达到预定收敛条件。设D维特征空间中有m个粒子,则粒子属性的迭代更新如式(4)所示:

由上述粒子群算法寻优的基本原理,LSSVM模型核参数寻优流程如图3所示,本文对长期车辆荷载作用下软基路堤的沉降预测步骤如下:

图3 LSSVM核参数优化流程
步骤1:使用有限元软件实现对软基路堤的模拟,并计算长期车辆荷载下的路基沉降数据;
步骤2:在MATLAB工具箱中采用PSO算法对LSSVM模型的高斯核函数进行优化,种群数量为20,最大迭代次数为200次,将最优参数组合作为输入变量,利用MATLAB编写LSSVM模型;
步骤3:利用MATLAB调取有限元数值计算结果,并将前2 500次车辆荷载作用下的软基路堤沉降数据作为训练样本输入PSO-LSSVM模型进行学习,后5 000次车辆荷载作用下的软基路堤沉降数据作为基准数据与PSO — LSSVM的预测结果进行比对,验证预测模型的有效性。
3 结果分析
3.1 模型建立及预测精度评价
为验证PSO — LSSVM模型的有效性,分别使用PSO-LSSVM模型、BP神经网络预测模型和双曲线路基沉降模型进行对比分析。其中,BP神经网络模型使用MATLAB中的神经网络工具箱,双曲线沉降数学模型如式(5)所示[7]:
(5)
式中:Dt为t时刻沉降量;D0为初始沉降量;t0路堤填筑完成时刻;α、β为回归系数。
选取绝对误差、相对误差及均方误差作为模型的预测精度评价指标,计算公式分别如式(6)~(8)所示:
ε=|xi-x′i|
(6)
(7)
(8)

3.2 数值计算及预测结果分析
以500次车辆荷载作用为一期,提取软基路堤沉降数据,共计提取15期数值计算结果,使用前5期2 500组数据作为样本数据进行拟合,后10期数据与预测结果进行对比,验证不同学习模型的预测精度,各预测模型误差如表2所示,沉降曲线如图4所示。
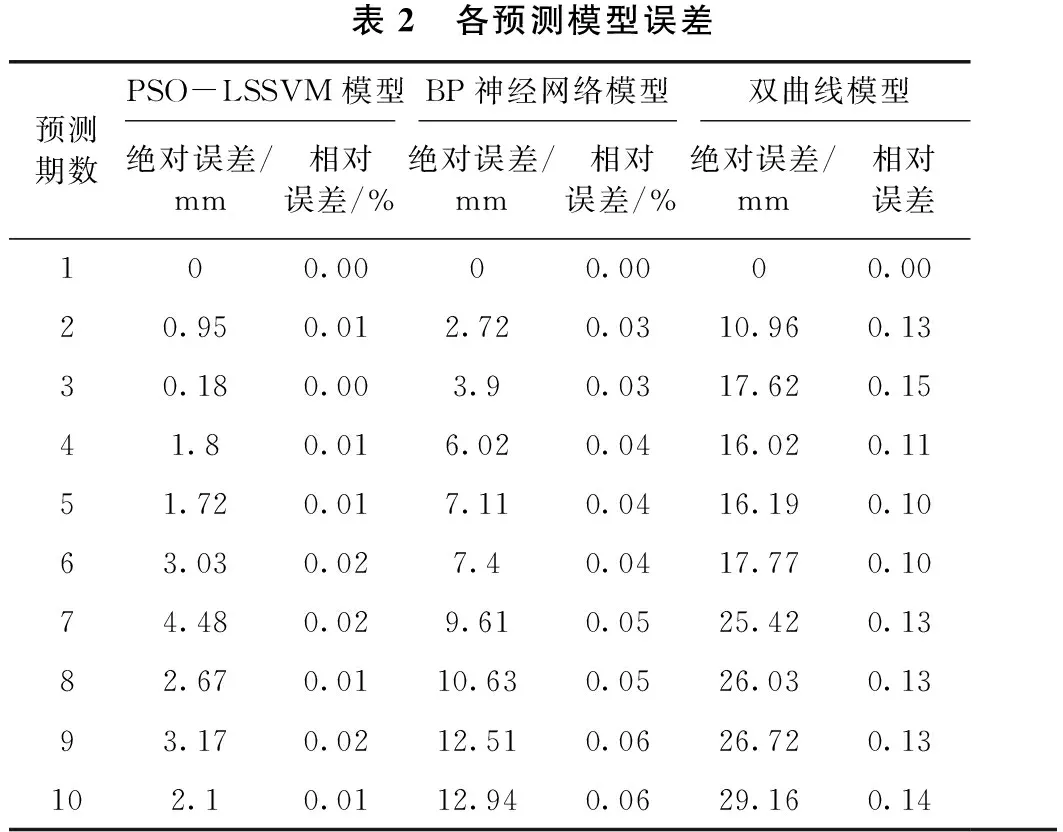
表2 各预测模型误差预测期数PSO-LSSVM模型BP神经网络模型双曲线模型绝对误差/mm相对误差/%绝对误差/mm相对误差/%绝对误差/mm相对误差100.00 00.00 00.00 20.950.01 2.720.03 10.960.13 30.180.00 3.90.03 17.620.15 41.80.01 6.020.04 16.020.11 51.720.01 7.110.04 16.190.10 63.030.02 7.40.04 17.770.10 74.480.02 9.610.05 25.420.13 82.670.01 10.630.05 26.030.13 93.170.02 12.510.06 26.720.13 102.10.01 12.940.06 29.160.14

图4 各模型预测结果对比
由表2、图4可知,经过粒子群算法优化后的最小二乘支持向量机对软基路堤在车辆荷载下的沉降变化,具有最好的拟合效果。其预测的沉降值与有限元数值计算结果基本吻合,相对误差控制在2%以内,均方根误差为2.41;BP神经网络预测模型的前5期预测结果与数值结果相差不大,但后5期预测数据逐渐偏离数值结果,且误差随预测期数增加而不断增大,最大相对误差为6%,均方根误差为8.33;双曲线模型对于软基路堤在车辆荷载下的沉降预测准确度较低,平均预测误差大于10%,均方根误差为20.38,预测精度明显低于基于机器学习的沉降预测模型。
3.3 软基路堤长期沉降趋势
在证明PSO-LSSVM模型有效性的基础上,为研究软基路堤在长期车辆荷载下的沉降趋势,使用PSO-LSSVM模型预测100 000次车辆荷载作用下沉降数据,以每10 000次车辆荷载下的沉降量为典型值进行采样,得到的长期沉降曲线如图5所示。

图5 长期车辆荷载作用下沉降预测
由图5可知,软基路堤在50000次车辆荷载作用后每期沉降值逐渐减小,并于90000次车辆荷载作用后逐渐趋于稳定,最终沉降量为520 mm左右。此外,软基路堤在长期车辆荷载作用下发生了一定的不均匀沉降,低坡侧的路基沉降量略大于高坡侧的路基沉降量,不均匀沉降差值在20 mm左右。
4 结论
软基路堤相较于普通路堤在长期车辆荷载作用下沉降量更大,且易发生不均匀沉降,影响路基的整体稳定性。本文在软基路堤有限元模型数值计算结果的基础上,建立了基于粒子群算法优化最小二乘支持向量机的路基沉降预测模型,分析了某软基路堤在长期车辆荷载作用下的沉降趋势,结论如下:
1) 采用有限元软件可以较为准确地实现车辆荷载下软基路堤的沉降计算,但计算量较大,不利于进行长期沉降分析。
2) 在训练样本有限的情况下对路基沉降的预测,采用粒子群算法优化后的最小二乘支持向量机模型效果最佳,其预测精度高于BP神经网络沉降预测模型和双曲线沉降模型,平均相对误差在2%以内。
3) 长期车辆荷载作用下某软基路堤的最终沉降量稳定在520 mm左右,高低坡存在一定的不均匀沉降差,低坡侧沉降量略大于高坡侧20 mm左右。
