纳入蠕变变形机理的宽范围应力区下P91钢本构模型

张经伟，昝静一，梁坤，刘康林

(福州大学石油化工学院，福建 福州 350108)

0 引言

随着化工、电力等工业的发展，长期处于超高温和复杂载荷条件下的结构，受蠕变变形、应力松弛、应力再分布等宏观行为的影响，微观上体现出微裂纹、微空隙以及其他微观缺陷的萌生和扩展等[1-2].大量实际案例表明高温结构的主要失效模式是蠕变裂纹扩展引起的结构破坏，在过去的100年中，蠕变裂纹扩展失效引起的化工事故占国际化工事故的一半以上[3].目前实际工程中广泛应用的高温结构蠕变寿命评估的技术方法包括Larson-Miller参数法、Manson-Haferd参数法等，这些方法都是基于线性外推法，由高应力下材料的短时蠕变试验数据线性外推得到低应力下高温构件的长时蠕变数据.但材料在低应力区和高应力区的蠕变变形机理不同，使得不同应力区下材料的蠕变变形行为不同，因此，从高应力区向低应力区线性外推获得的结构蠕变寿命评估结果往往与实际结构的断裂寿命相差甚远[4].

大量试验表明，合金材料的蠕变变形机理与应力水平相关[5].在低应力区，蠕变变形机理是扩散蠕变或Nabarro-Herring(N-H)蠕变，主要受晶格扩散作用的影响；在高应力区，蠕变变形机理是幂律蠕变，主要是位错攀移-滑移到仅有位错滑移过程；在过渡应力区，蠕变变形机理是扩散蠕变和幂律蠕变同时发生[6-8].因此在高温结构蠕变寿命评价时，需要发展一种能够在宽范围应力区(低应力区、过渡应力区、高应力区)描述材料蠕变变形行为的本构模型.

此外，材料的长期热老化会导致材料的微观结构变化并产生M23C6沉淀物，进而导致材料劣化，使得材料抗蠕变性能下降[9-11].因此，在构建宽范围应力水平下材料的蠕变本构模型时，不仅要考虑不同蠕变变形机理的影响，还需要纳入材料热老化的影响.本研究对不同应力区蠕变变形机理进行分析，构建一个基于宽范围应力区的蠕变本构模型，并通过已有P91材料试验数据确定模型参数，将该模型编写成有限元子程序，并嵌入到有限元中通过模拟单轴蠕变拉伸试验来验证模型的准确性.本研究可为后续宽范围应力区材料蠕变变形行为的预测以及高温结构蠕变寿命评价工作提供模型支撑.

1 基于蠕变变形机理的CDMWRS本构模型构建

在高温条件下，材料的蠕变变形机理为扩散蠕变占主导[12].Nabarro首次提出了扩散蠕变机制的理论方程，Herring对其进行了改进并提出了N-H蠕变方程，Coble认识到晶界扩散的作用, 也提出相应的蠕变方程，晶格扩散和晶界扩散均独立地引起蠕变[8].因此总的蠕变应变速率为晶格扩散产生的蠕变应变速率和晶界扩散产生的蠕变应变速率之和，结合Arrhenius方程，扩散蠕变对应的蠕变应变速率表达式如下

(1)

在高应力区回复蠕变理论研究的是纯金属材料的位错运动微观机理，位错蠕变变形机理由Harper和Dorn首次提出[8].根据Orowan机制，位错蠕变的蠕变应变速率方程写为

(2)

试验研究表明，在高温下，由于原子扩散较快，材料中的贝氏体会加速消失，原始微观结构中的M7C3和M23C6碳化物全部转化生成M23C6沉淀[13-14]，这使得P91钢材料的蠕变强度降低，进而造成材料蠕变应变速率增加，断裂时间相比之前未服役的材料减小.由于M23C6沉淀物数量密度和尺寸对孔洞成形有影响，主要表现为M23C6析出物的数量密度与位错运动的阻力呈正相关，尺寸和位错运动的阻力呈负相关，这导致材料的断裂时间减小和蠕变应变速率增大[13].因此有必要考虑M23C6沉淀的弥散强化影响，引入门槛应力σth[11]，其相应本构方程为

(3)

其中：A为材料常数；m为有效应力指数；σ为施加应力；σth为门槛应力；σ0为参考应力；Q为蠕变活化能；T为开氏温度；R为通用材料常数. 参数m与材料的温度无关[8]. 参数m值确定后，根据试验数据，门槛应力值σth可以在不同温度下进行调整和确定[11].

通过上述分析可知，材料在低应力区发生扩散蠕变，蠕变应变速率与应力呈线性关系；在高应力区发生幂律蠕变，蠕变应变速率和应力呈幂函数关系；此外在整个蠕变过程中还存在发生热老化现象，则需考虑门槛应力σth.因此，高温结构随着时间的推移，其经过低应力区、过渡应力区、高应力区以及热老化的影响，则材料蠕变变形的总蠕变应变速率可以写为

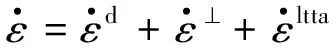
(4)

其中： ⊥代表位错蠕变过程；d代表扩散蠕变过程；ltta代表长期热老化过程.把式(1)～(3)代入式(4)可得

(5)

当温度一定时，Arrhenius方程为一个具体数值，因此可以将式(5)简化为

(6)

其中：σ0是参考应力，表示从线性蠕变到幂律蠕变行为的过渡；m和n是应力指数；Ai是材料参数.由于位错蠕变的蠕变应变速率方程在形式上与长期热老化的蠕变应变速率方程相似，位错蠕变项和长期热老化项合并为一项，因此式(6)可以进一步简化为

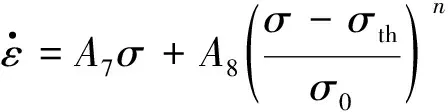
(7)

当σth=0时，表示不考虑某些合金材料的长期热老化影响，适用于分析短期服役材料.对于长期工作的设备组件(例如P91钢制成的设备组件在600 ℃下持续服役100 000 h[10])，则不能忽略门槛应力σth.基于蠕变变形机理的CDMWRS本构模型，得到的材料总蠕变应变速率是基于几个蠕变过程的蠕变应变速率加和，因此接下来探究这些蠕变过程之间的影响，以及对总蠕变应变速率的影响.

2 本构模型分析

2.1 变形机理对本构模型的影响

对于宽范围应力水平下服役的设备结构，材料的蠕变变形机理与应力水平相关.低应力区发生扩散蠕变或N-H蠕变，蠕变应变率与应力之间存在线性关系，应力指数n为1；高应力区发生幂律蠕变，蠕变应变率与应力之间存在幂函数关系，应力指数n为3～7甚至更高；宽范围应力区发生热老化，产生的M23C6析出碳化沉淀物会削弱材料的蠕变强度，并减小材料的断裂时间.

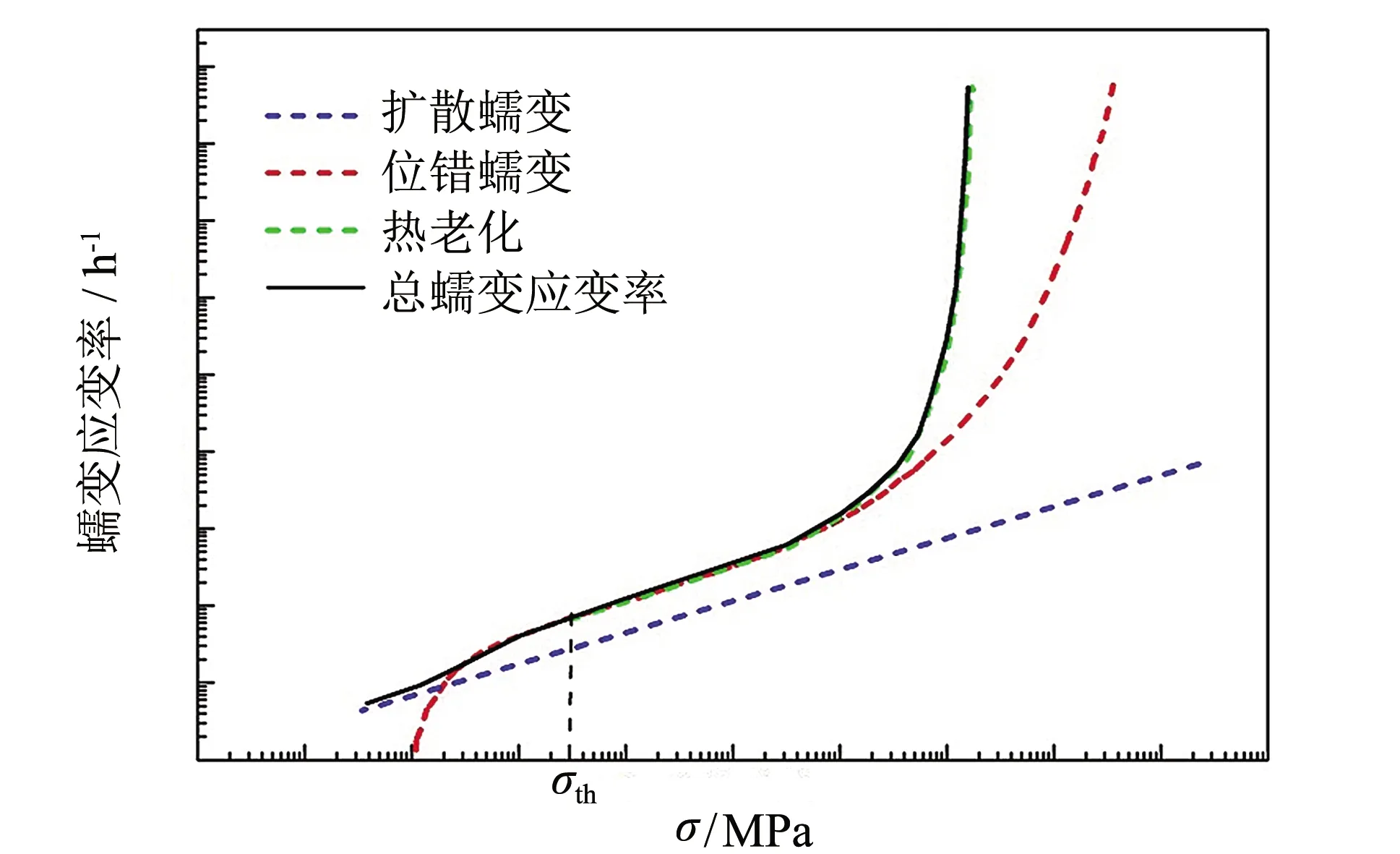
图1 P91钢的宽范围应力区蠕变应变率趋势图Fig.1 Trend diagram of creep strain rate in wide range of stress areas for P91 steel

不同应力区的蠕变变形机理如图1所示，图中的4条曲线分别表示总蠕变应变速率、扩散蠕变、位错蠕变和热老化.在低应力区，应力指数为n=1的扩散蠕变在蠕变变形过程中占主导，扩散蠕变控制的蠕变应变速率大于位错蠕变控制的蠕变应变速率；随着应力水平增大，蠕变变形过程中应力指数n>>1的位错蠕变占主导，此时位错蠕变控制的蠕变应变速率大于扩散蠕变控制的蠕变应变速率；随着蠕变时间的增加，材料组织发生变化，此时热老化对蠕变裂纹扩展速率产生显著影响.与不考虑热老化过程的材料相比，热老化过程中M23C6碳化物的产生和沉积导致材料的蠕变强度降低，蠕变应变速率增加，以及断裂时间缩短.因此，高温结构从开始服役到最终的断裂，其蠕变变形是上述不同变形机理作用下产生的蠕变变形量的综合体现.基于以上分析可以得到，这些蠕变过程之间不可否认会有一定影响，但是在不同应力区这些蠕变过程相互的影响又几乎是可以忽略的，因此叠加后这些蠕变过程互相之间的综合影响可以忽略，接下来进一步讨论前面构建的CDMWRS模型与已有本构模型的差别，并进一步通过有限元模拟验证CDMWRS模型的准确性.

2.2 本构模型参数的确定

以600 ℃下P91钢为对象，选择Norton模型、2RN模型、双曲正弦函数模型以及本文构建的CDMWRS本构模型进行研究.为了获得不同本构模型参数，基于文献[11, 15]的试验数据，对Norton模型、2RN模型、双曲正弦函数模型以及CDMWRS本构模型分别进行拟合，结果如图2所示，不同本构模型参数见表1.

从图2可以看出, 单机理本构Norton模型对高应力区的试验数据拟合较好，但是无法表征低应力区蠕变应变率与应力关系.双曲正弦模型通过拟合从单轴蠕变试验得到的蠕变应变速率-应力数据获得蠕变本构方程，虽然对高应力区的数据拟合较好，但对过渡应力区的数据拟合较差，并且无法对低应力区的数据进行较好的拟合.双机理本构2RN模型，是对高应力区和低应力区分别采用不同参数值的Norton模型进行拟合，但不同应力区存在一个转折点，而实际不同应力区的划分时很难准确区分，此外转折应力的不同会导致过渡应力区的数据拟合十分不准确.基于蠕变变形机理的CDMWRS本构模型克服了上述模型的不足，在宽范围应力区和试验数据能进行很好的关联.

表1 不同蠕变本构模型参数

图2 不同本构模型参数的拟合Fig.2 Fitting of various constitutive models parameters

3 CDMWRS本构模型的有限元验证

3.1 有限元模型

有限元模型采用单轴蠕变圆棒试样，600 ℃下P91钢材料的杨氏模量E和泊松比λ分别为121 GPa和0.3，真应力-应变曲线参见文献[16]中的图2.圆棒直径为10 mm，尺寸如图3(a)所示.

有限元网格划分如图3(b)所示，载荷通过RP参考点加载，该参考点与圆棒左端外表面耦合，以近似模拟试验过程中的螺纹加载.有限元模型网格采用三维八节点缩减积分单元C3D8R，总共包含3 135个节点及2 520个单元.将CDMWRS本构模型写入CREEP子程序，嵌入ABAQUS软件中来模拟单轴蠕变拉伸试验.

3.2 结果讨论

为对比不同应力水平条件下试验结果，分别模拟4组100、120、160和200 MPa与试验相同载荷水平单轴蠕变拉伸试验.模拟数据去掉弹性阶段，如图4所示，可以看出尤其是在低应力条件下，有限元模拟得到的蠕变应变-时间数据曲线和试验数据在蠕变第一阶段和第二阶段吻合较好.但蠕变第三阶段模拟结果与试验数据差别较大，主要原因是因为该本构中未纳入损伤的影响，即忽略了材料中微观腔洞的成形、生长和扩展引起的材料强度、刚度和韧性降低以及蠕变寿命大大缩短[17]，因此模拟得到的应变-时间曲线在低、中应力区与试验数据吻合较好.

图3 单轴蠕变圆棒试样Fig.3 Uniaxial creep round bar sample

图4 不同应力条件下的P91钢蠕变曲线Fig.4 Creep curve of P91 steel under different stress levels

图4中的对比可以说明，该本构模型可以很好地反映高温P91钢结构在不同应力水平条件下的蠕变变形行为，且拟合得到的CDMWRS本构模型参数对高温P91钢具有较好的可靠性和适用性.若将该本构应用于其他材料，则需部分实验确定CDMWRS模型参数即可.此外，结合相应的损伤方程可将该模型用于高温结构的蠕变裂纹扩展寿命评价.

4 结论

以P91钢为研究对象，通过分析不同应力水平下材料的变形机理，构建适用于宽范围应力区的基于蠕变变形机理的CDMWRS本构模型，并通过对比已有文献数据进行模型验证，主要结论如下:

1) 宽范围应力区材料的蠕变变形机理与应力水平相关，在低应力区的蠕变变形机理是扩散蠕变，在高应力区是位错蠕变，在长期热老化过程中碳化沉积物也会增大材料的蠕变应变速率，综合考虑其影响后构建了CDMWRS模型，根据相关试验数据确定CDMWRS模型参数.

2) 采用ABAQUS软件，结合构建的CDMWRS模型模拟不同载荷水平下的单轴蠕变拉伸试验，模拟结果与试验数据在蠕变第一阶段和第二阶段吻合较好，验证了CDMWRS模型的准确性和可靠性.由于模型未考虑损伤的影响，蠕变变形第三阶段与试验数据相差较大.