一类具有强弱奇性的Duffing方程周期正解的存在性
2022-01-20宋娟王振辉程志波
宋娟, 王振辉, 程志波
(河南理工大学数学与信息科学学院, 河南 焦作 454003)
1.引言
近些年来, Duffing方程在物理、化学、机械、经济和电子技术中有着广泛的应用.一方面工程实际中的许多非线性振动问题的数学模型都可以转化为该方程来研究, 如船的横摇运动、结构振动、化学键的破坏、微弱周期信号检测、电力系统周期振荡分析、横向波动方程的轴向张力扰动模型等[1-3]; 另一方面在经济领域的混沌研究中, Duffing方程作为刻画系统状态的重要模型在分析中有着广泛应用.例如A.Bernabe等基于混沌理论, 利用Duffing方程对原油价格的动力学性质进行了研究[4-6].因此, Duffing方程的研究引起了国内外学者的广泛关注, 有很多学者把研究重点放在了半线性Duffing方程解的性态研究, 如周期解、有界解、拟周期解、解的个数以及解的稳定性的研究; 然而, 这些研究主要是集中在强奇性微分方程, 而对于具有弱奇性Duffing方程的研究却没有涉及.直到2007年以来, 国内外学者开始利用Leray-Schauder选择原理与锥压缩锥拉伸等不动点定理来证明相关问题.[7-9]近些年来, 有很多学者把研究重点放在了奇性Duffing方程周期解的研究.[10-14]例如, 在文[13]中, 王在洪研究了Duffing方程

其中g ∈C(R,R),e ∈C(R,R)是一个T-周期函数,g(x)满足半线性条件
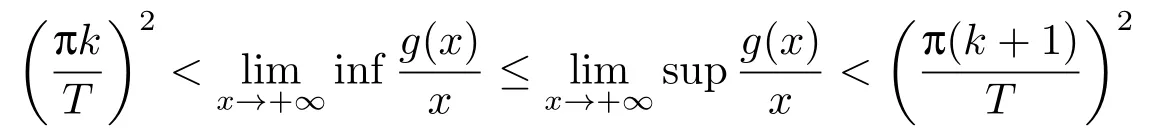
并且g(x)满足强排斥型奇性, 即
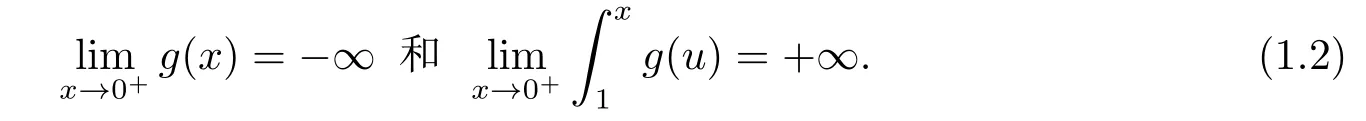
上述文章主要讨论了强排斥型奇性Duffing方程周期正解的存在性, 而如果方程(1.1)强弱奇性同时存在, 如果方程(1.1)具有吸引型奇性, 这些问题有待进一步的研究.本文, 我们利用Manasevich-Mawhin连续定理, 研究方程(1.1)在强弱奇性同时存在下正周期解的存在性.
2.主要结论
首先, 我们给出Manasevich-Mawhin连续定理, 对于T-周期的边值问题
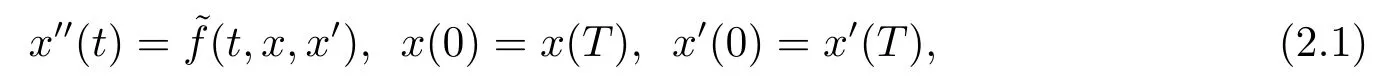
引理2.1[15]令Ω是在:={x ∈C1(R,R), x(t+T)≡x(t), ∀t ∈R}上的有界开集.并且满足下列条件:
(i) 对每一个λ ∈(0,1)
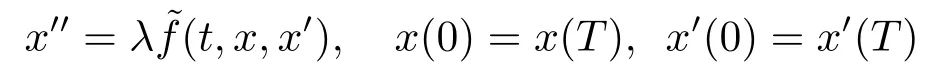
在∂Ω上没有解;
(ii) 方程
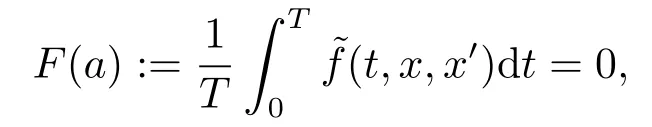
在∂Ω ∩R上没有解;
(iii)F的Brouwer度
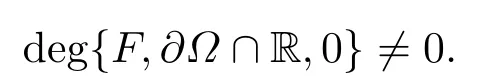
接下来, 利用引理2.1, 我们得到下面的结论.
定理2.1假设下列条件成立:
(H1)g(x)是单调递增函数;
(H2) 存在正常数a,b使得对所有的x ∈(0,+∞), 有g(x)≤ax+b;
(H3) 下列不等式成立
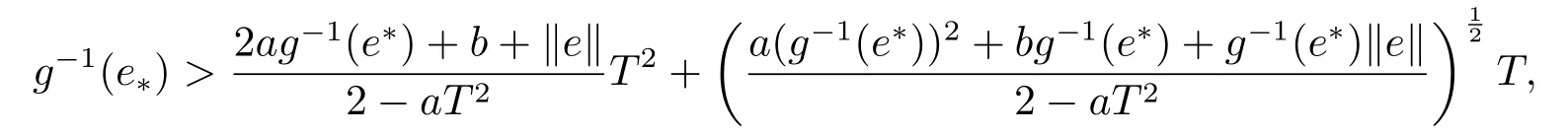

由(H1)条件, 我们得
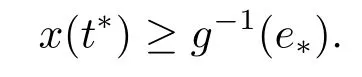
同理, 我们有
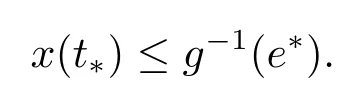
自x(t)的连续性, 则我们知道存在ξ ∈(0,T), 使得

由(2.3), 我们有
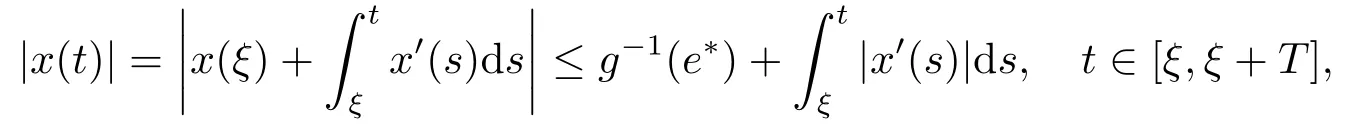
并且
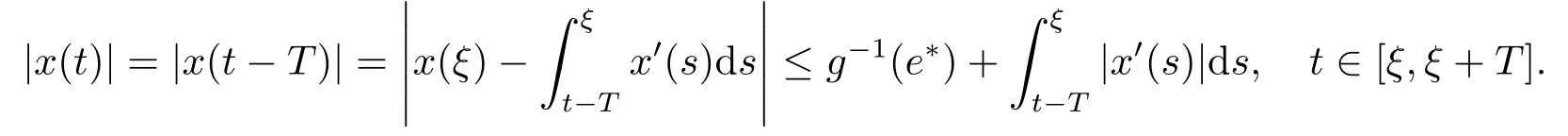
结合上面两个不等式, 我们得到
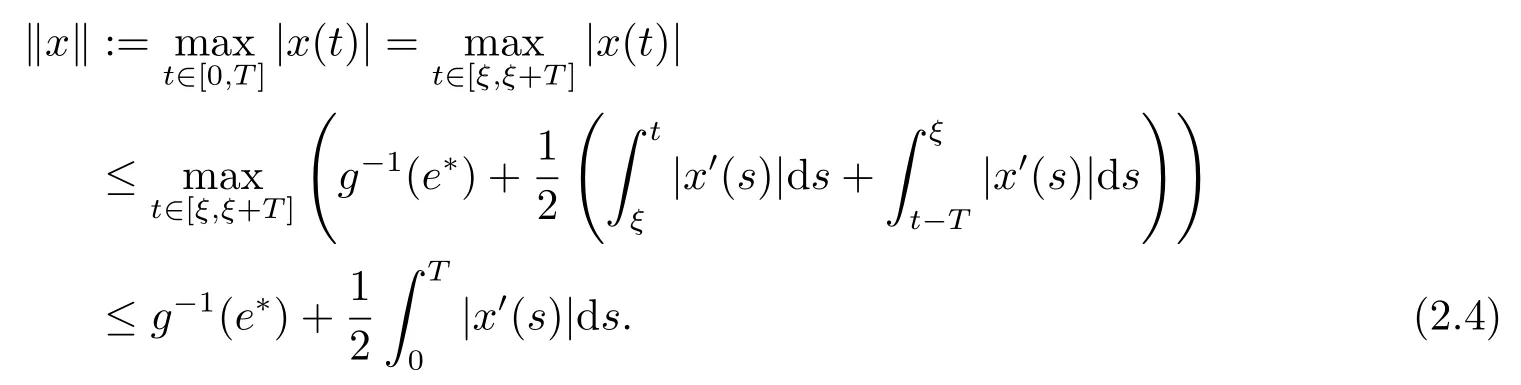
方程(2.2)左右两边同乘以x(t) 并进行0到T的积分, 我们有


这里g+(x)=max{g(x),0}.
由式子(2.5)和(2.9), 我们有
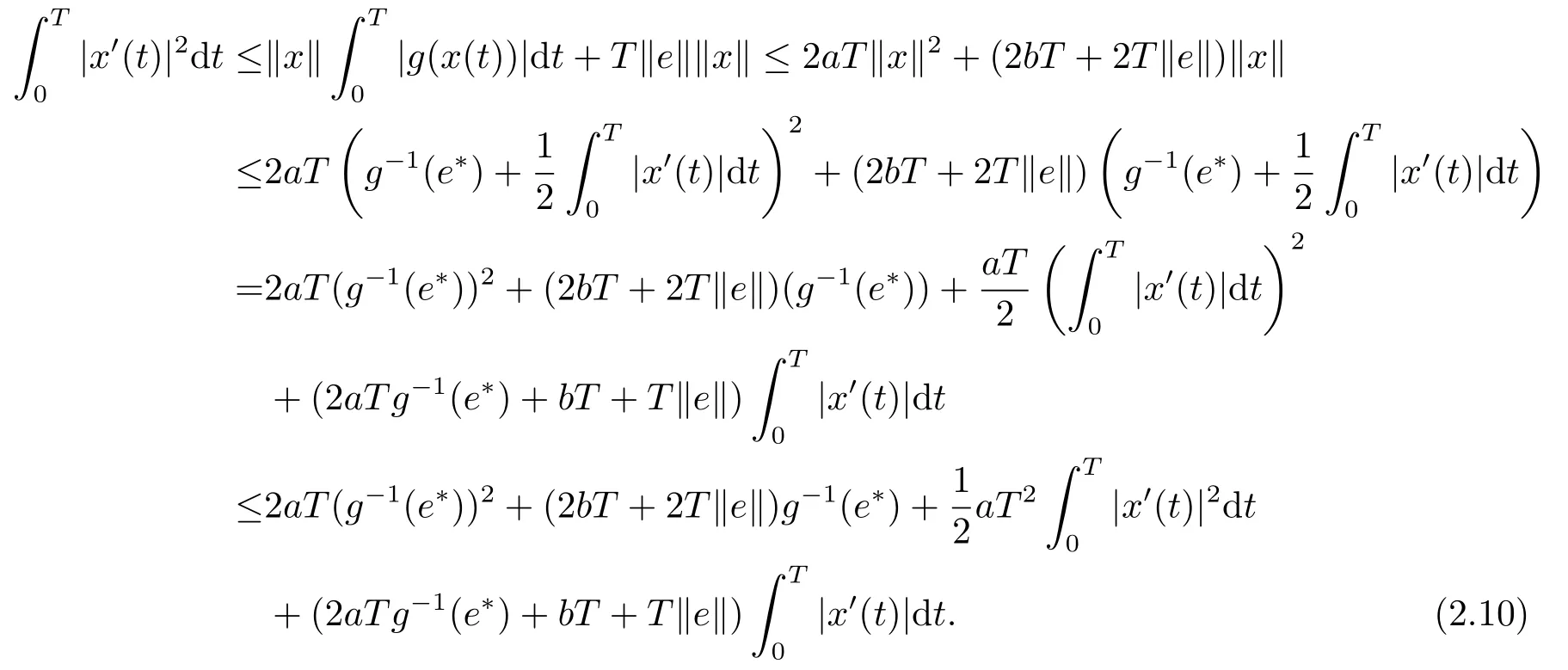
更进一步, 我们得
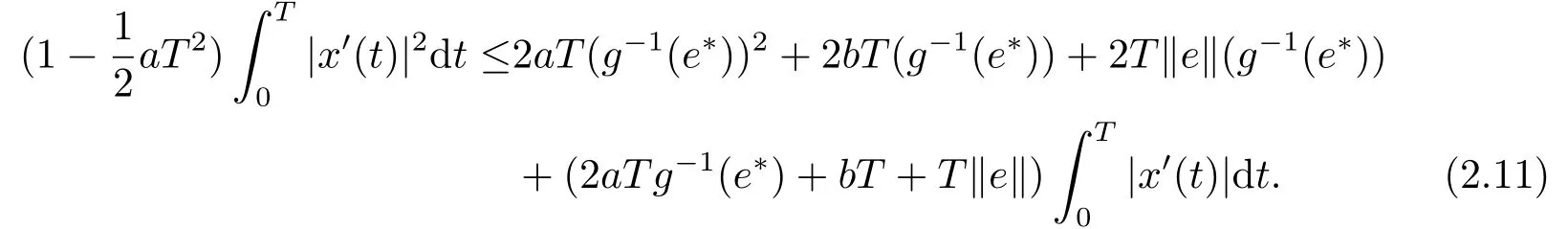

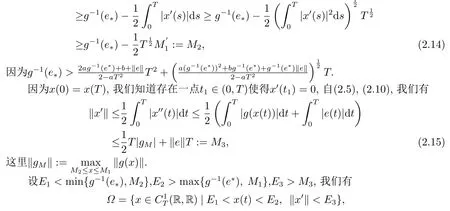
我们知道对于λ ∈(0,1), (2.2)在∂Ω上没有解并且当x(t)∈∂Ω ∩R, x(t)=E2或x(t)=E1.存在E使得
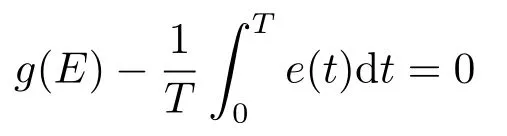
且满足E ∈(E1,E2).则引理2.1的条件(i)和(ii)成立.
接下来, 我们考虑引理2.1中的条件(iii).自(H1), 我们得到

定理2.2假设下列条件成立:
(H4)g(x)是单调递减函数;
(H5) 存在正常数a,b使得对所有的x ∈(0,+∞), 有-g(x)≤ax+b;
(H6) 下列不等式成立
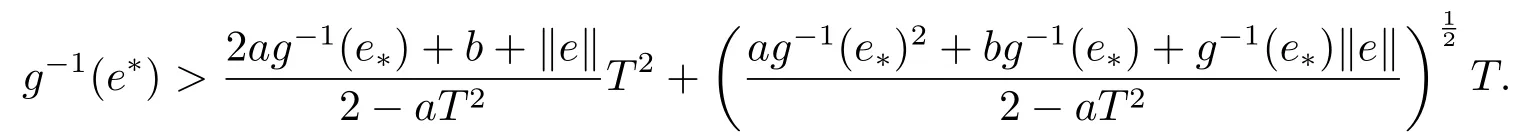
通过下面的例子来阐明我们的定理.
例2.1考虑下面带阻尼的奇性Duffing方程

