纵向数据下非参数带测量误差的部分线性变系数模型的估计
2022-01-20王鹏鹏肖燕婷
王鹏鹏, 肖燕婷
(西安理工大学理学院应用数学系, 陕西 西安 710054)
1.引言
纵向数据广泛应用于医学、生物学、社会学、金融学和经济学等诸多领域.它是指对同一个受试个体在不同时间点上重复观测若干次, 从而得到的由截面数据和时间序列数据结合在一起的数据.纵向数据的最大特点是对不同个体观测数据是独立的, 但对同一个观测个体所得到的数据往往具有相关性.因此, 在分析纵向数据时, 需要充分考虑个体内的相关性, 如果忽略这种相关性, 会对兴趣参数的估计造成偏差, 从而降低统计推断的可靠性.LIANG和Zeger[1]提出的广义估计方程(GEE)方法, 通过估计工作相关矩阵中的调谐参数, 可以得到模型中参数的相合估计, 但当工作相关矩阵被错误指定时, 调谐参数的矩估计使得对感兴趣参数的估计并不是最优的.为此, QU等[2]提出了二次推断函数(QIF)方法, 该方法不仅可以提高估计的效率, 还能得到比GEE方法更加有效和稳健的结果.
部分线性变系数模型作为一类重要的半参数模型, 不仅具有参数模型的可解释性, 又具有非参数模型的灵活性, 在实际应用中有着广泛的适用性.一经提出, 就得到了众多学者的广泛关注.该模型的研究已经取得了一系列丰硕的成果, 主要集中在模型中参数和系数函数的估计、变量选择及相关检验等方面.考虑纵向数据下的部分线性变系数模型

其中Yij ∈R和(Xij,Zij)∈Rp ×Rq分别为第i个个体的第j次观测的响应变量和协变量,εij ~N(0,Σ2)且εij与(Xij,Zij)相互独立.β= (β1,β2,··· ,βp)T为p维未知参数向量,α(t) =(α1(t),α2(t),··· ,αq(t))T为q维未知函数向量.E(Yij|Xij,Zij,tij)=μij,Var(Yij|Xij,Zij,tij)=V(μij), 其中μij为Yij的条件均值,V(·)为已知方差函数.针对模型(1.1), ZHAO和XUE[3]提出了一种组经验似然方法处理纵向数据的相关性; TIAN等[4]结合基函数近似和二次推断函数, 提出了模型的变量选择方法; WANG和LIN[5]提出了一种稳健的变量选择方法;ZHAO和YANG[6]提出了一种基于正交分解技术的参数估计方法.
在实际数据分析中, 经常会遇到协变量不能精确观测的情形, 直接忽略测量误差往往会导致估计量不再是无偏估计.因此, 对测量误差的纠偏成为统计学的研究热点之一.针对部分线性变系数模型, 早期的研究主要集中在参数协变量X不能精确观测, 带有可加型测量误差的情形, 如YOU和CHEN[7]在测量误差协方差阵已知情形下, 给出了模型中参数和非参数的估计; WANG等[8]利用经验似然方法, 构造了模型中参数的经验似然置信域估计; TIAN和XUE[9]在纵向数据下, 提出了偏差修正的的参数估计和变量选择方法.然而,除了参数协变量不能精确观测以外, 在现实中, 还会遇到非参数部分带有测量误差的情形, 即Z带有可加型测量误差,X和U可以精确观测.针对非参数协变量Z带有测量误差的部分线性变系数模型, FENG和XUE[10]提出了参数分量的局部纠偏剖面最小二乘估计方法; 冯三营等[11]和FAN等[12]基于经验似然方法研究了模型中参数和系数函数的置信域估计;FAN等[13-14]将模型推广到高维情形, 分别基于惩罚经验似然和惩罚最小二乘方法给出了模型的估计.但以上成果研究的都是横截面数据, 针对纵向数据下非参数部分带有测量误差的情形,还少有研究.
本文主要研究非参数部分带有可加型测量误差时, 纵向数据下的部分线性变系数模型, 提出模型中未知参数和系数函数的估计方法, 证明估计量的大样本性质, 并用模拟试验和实际算例说明所提方法对测量误差的纠偏是有效的.
2.估计方法
考虑纵向数据下非参数部分带有测量误差的部分线性变系数模型, 形式如下

由于某些原因, 协变量Zij不可观测, 真正观测到的是替代变量Uij, 测量误差ξij满足E(ξij)=0,Cov(ξij)=Σξ.
记B(t) = (B1(t),B2(t),··· ,BL(t))T为M阶的B样条基函数, 其中L=K+M,K为B样条内节点的个数, 根据HE等[15]的思想, 系数函数αk(t),k= 1,2,··· ,q,可表示为αk(t)≈B(t)Tγk,其中γk为L×1维未知B样条回归系数向量.
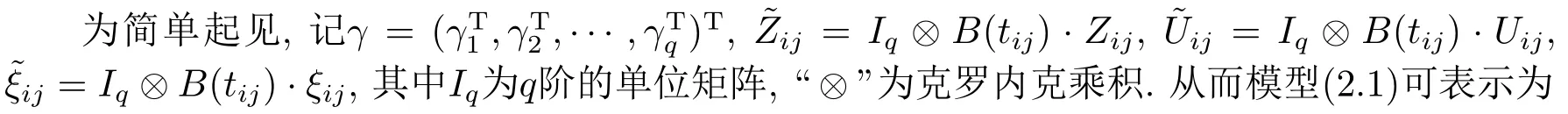
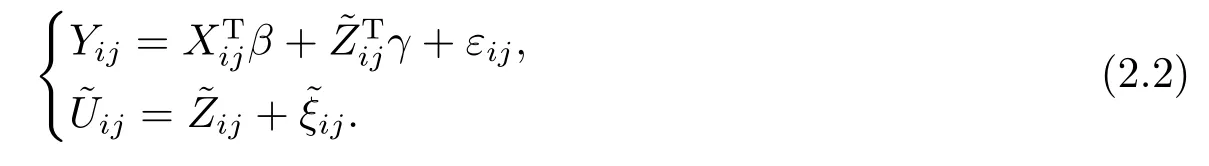
基于模型(2.2), 利用LIANG[16]提出的纠偏思想, 定义如下未知参数的偏差修正的广义估计方程(GEE)




其中Mk为已知的基矩阵,ak为未知参数.将(2.4)式带入(2.3)式, 得到新的偏差修正的广义估计方程为

这里, 并不需要估计未知参数ak, k=1,2,··· ,s.按照QU等[2]的思想, 可以定义如下的扩展得分向量Gn0(θ)为


基于(2.8)式, 关于θ的基于二次推断函数的偏差修正目标函数为


最终, 系数函数αk(·)的估计为


3.主要渐近性质
本节讨论上述估计结果的相关性质, 首先给出一些基本的假设.


结合假设4和假设6可知,∀a ∈Rp+qL, 满足aTa= 1, E(aTNi) = 0, supiE(‖aTNi‖)≤‖a‖supi‖Ni‖3, 其中aTNi满足中心极限定理

证假设δ=n-r/(2r+1), 令β=β0+δΔ1,γ=γ0+δΔ2, Δ = (ΔT1,ΔT2)T.下证∀ε >0,∃C >0, 使得
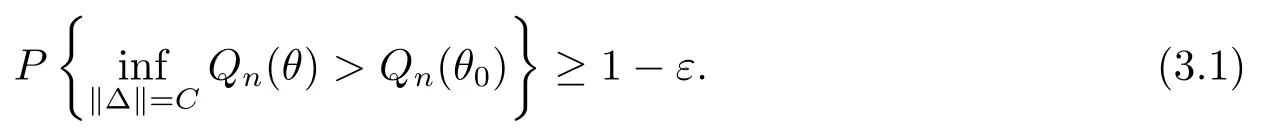
对Qn(θ)在θ0点泰勒展开, 可得,

由引理1和2可知

和

故有


通过计算可得


4.模拟试验
本节通过模拟试验来验证所提估计方法在有限样本下的具体表现.数据生成过程为

其中参数向量β= (1.5,0.8,2)T, 系数函数向量α(u) = (α1(u),α2(u))T,α1(u) = 5.5 +0.1exp(2u -1),α2(u) = sin(2πu).协变量Xij ~N(2,I3),Zij ~N(2,I2),tij ~U[0,1],模型误差向量εi ~N(0,Corr(εi,ρ)), Corr(εi,ρ)为已知的相关矩阵, 这里取一阶自回归矩阵(AR-1)和可交换矩阵(EX)两种不同的相关矩阵, 相关系数ρ= 0.2,0.5,0.8分别表示低度相关、中度相关和高度相关.测量误差ξij ~N(0),Σξ= 0.2,0.4分别代表两种不同情形的测量误差,i= 1,2,··· ,n,j= 1,2,··· ,5.样本容量分别取为n= 150,200,300, 重复200次模拟试验.
为了评价本文所提方法对参数分量的估计效果, 考察参数估计偏差(Bias)和均方误差(MSE)两个指标.表1和表2分别给出了当相关系数取中度相关ρ=0.5时, 不同相关结构下参数估计的效果, 其中, “QIF”表示偏差修正的二次推断函数方法, “NQIF”表示忽略测量误差的二次推断函数方法.

表1 AR-1 相关结构下参数估计的偏差和均方误差

表2 EX相关结构下参数估计的偏差和均方误差
表1和表2结果表明: 1)修正偏差的二次推断函数方法(QIF)下的偏差(Bias)和均方误差(MSE), 都要比忽略测量误差方法(NQIF)下的小, 说明偏差修正方法是有效的; 2)两种估计方法的均方误差差别不大, 这可能是由于非参数部分存在测量误差, 而参数部分没有测量误差导致的; 3)随着测量误差的减小, 两种方法估计的偏差和均方误差都变小; 4)随着样本量的增大, 两种方法的偏差和均方误差显著减小, 且QIF较NQIF方法估计的结果更加稳定.
进一步, 利用均方误差平方根(RASE)来评价非参数函数的估计效果,其中

其中ut(t= 1,2,··· ,M)为(0,1)区间上等距的格子点,M= 200.表3和表4分别给出了两种不同相关结构下系数函数的估计效果.

表3 AR-1相关结构下非参数估计的RASE

表4 EX相关结构下非参数估计的RASE
通过表3和表4可以看出: 1)在大部分情形下, 偏差修正的二次函数方法(QIF)下的RASE值都比忽略测量误差方法(NQIF)下的值要小, 说明所提偏差修正方法是有效的; 2)随着测量误差的减小, 两种方法的估计效果都变的更好, 尤其是QIF方法表现甚佳; 3)随着组内相关程度的增大, 两种方法的估计效果均有变弱的趋势; 4)随着样本容量的增大, 两种方法的估计效果都变得更好, 且QIF方法的估计效果较NQIF方法的估计效果更佳.
5.实例分析
本节分析1984年到1991年期间感染HIV的185名同性恋患者的艾滋病(AIDS)群体研究数据.赵培信[18]采用部分线性变系数模型分析了该数据, 杨宜平和李佳[19]利用变系数EV模型分析了该数据.数据包含观测时间, 记为tij; 吸烟情况, 记为X1ij, 取值为0表示感染HIV后不吸烟, 取值为1表示感染HIV后吸烟; 患者感染HIV时的年龄, 记为X2ij; 感染HIV以前血液中CD4细胞含量的百分比, 记为Zij; 目前血液中CD4细胞含量的百分比, 记为Yij.利用该数据建立如下的部分线性变系数模型

类似于杨宜平和李佳[19]的研究, 假定非参数协变量Zij含有测量误差, 即Uij=Zij+ξij.
测量误差ξij服从N(0假定的取值分别为= 0,= 0.17, 和= 0.34三种情况.这里, 组内相关结构选取为AR-1结构.
表5给出了两种不同测量误差及不考虑测量误差时参数的估计效果, 说明吸烟状况对血液中CD4细胞的百分比含量表现显著, 并且为正相关; 而年龄因素不是特别显著; 若协变量数据带有测量误差, 本文所提的纠偏方法是有效的.图1给出了各种情形下非参数函数α(t)的估计,可以看出感染前血液中CD4细胞含量的百分比对目前的CD4细胞含量的百分比有着较强的相关性.

表5 AIDS 数据不同测量误差下的参数估计
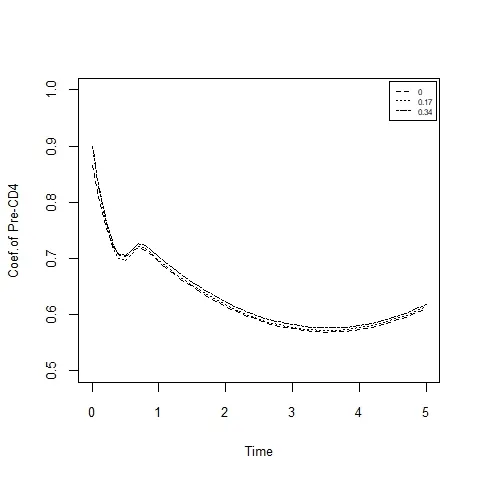
图1 AIDS数据不同测量误差下α(t)的估计
6.结论
部分线性变系数模型融合了参数模型的可解释性和非参数模型的灵活性, 是一类重要的半参数模型, 可以描述许多实际问题, 有较强的解释能力.纵向数据具有个体间独立、个体内相关的特征, 同时综合了截面数据和时间序列数据的特点.测量误差数据在一些实际问题中比较常见.本文研究的纵向数据下非参数部分带有测量误差的部分线性变系数模型的估计问题具有一定的理论价值和现实意义.利用B样条基对模型中的变系数函数进行近似, 构造了偏差修正的二次推断函数, 得到了模型中回归参数和变系数函数的估计.在一定的假设条件下, 证明了估计量的大样本性质.模拟试验和实例分析说明了本文所提方法的有效性.
