浅谈某城市应急物流中心选址问题

文/苏静静 朱晓溶

近几年我国经济不断发展，城市化进程加快，城镇化水平也日益提升。但在城市正常发展的背后，一旦发生重大突发事件，会对城市造成严重威胁。城市成为了重大的灾害发生区域，也成为了国家和社会大力防灾减灾的重中之重。在这样的背景下，与一般的物流服务以总成本极小化作为目标不同，应急物流服务要求以时间效率极大化和尽可能满足受灾区域为目标。在这种情况下，本文以2008年5月12日四川省汶川地震受灾区域数据进行研究，根据不同的灾情严重程度地区进行分类，通过聚类分析方法设置应急物流设施服务中心的位置[1]。

1.引言：

地震灾害具有突发性、瞬时性等特点，我国地震预报目前尚未可以做出临震预报。最近几年，我国地震大频率的发生，严重影响社会的日常运作[2]。2020年的新冠疫情事件，各地封村封路，物资调配不及时，一定程度反映着我国应急管理建设的不足。类似上述这种重大突发事件的情况，我国政府逐渐开始注重应急管理的建设，而应急物流作为应急管理体系中不可或缺的部分，承担着保障突发事件应急处理过程中的物资需求的重任[3]。对应急物流服务设施中心选址问题成为了应急物流系统研究中的一个重点[4]。本文针对灾害损失程度相对分类的应急物流服务设施中心选址[5]，运用无监督学习的聚类方法对受灾点的进行分类，将受灾区域程度较严重的受灾点作为应急物流服务设施节点，在应急物资一定的条件下满足应急物流对效率性和公平性的要求[1]。

2.相关理论概念

2.1 地震等级划分。地震有烈度和震级两大因素，烈度用来表示地震的破坏力度，震级用来表示地震自身的大小。我国地震局将地震划分为天然地震、人工地震和脉动，将经济损失与受伤和死亡人数为指标用于区别地震灾害等级。例如，将具有重大经济损失且直接经济损失不超过该省上年生产总值1%、伤亡人数在50-300人，震级在6.5级-7.0级划分为重大地震。

2.2 聚类分析理论。聚类分析方法是对于事先不清楚数据集合中每一个数据的类别且没有其他的先验知识的背景下，根据数据特征进行无监督的分类[1]。聚类分析方法属于无监督学习[6]。通俗的来说，聚类分析就是无监督的根据集合中数据的特征使集合中具有相似特征的数据聚集一起，不相似的数据进行分离。k-m eans算法以数据间的距离作为数据对象相似性度量的标准。常用计算距离的方式有：余弦距离、欧式距离、曼哈顿距离和欧式距离公式[1，7]。

3.算法设计

3.1 灾难相对分类。根据每个受灾区域的伤亡人数和经济损失数据通过聚类分析方法对不同程度的受损区域进行分类，以选取出灾损程度较严重的受灾点[5，8]。假设类wi和wj类之间的距离是d（wi，wj），则两类之间的最近距离是类wj中所有样本与类中所有样本间的最小距离。d（wi，w ）j=m in d（X，Y） （X∈wi，Y∈wj）

通过python对各受灾区域数据进行聚类分析设计，总结可知将灾区分为两类[9]。第一类(重大灾区)：汶川县、青川县、绵竹市、平武县、北川县与成都市等。第二类（严重灾区）：彭州市、茂县、江油县、理县、雅安与眉山等。根据百度百科对汶川地震受灾区域的划分相对比[10]，聚类分析进行分类差异不大。

3.2 对受灾区域进行距离聚类。所有受灾区域按坐标利用k-means方法进行聚类分析[1]。首先对所有受灾区域进行坐标统计，利用Jupyter Notebook得出聚类结果。将受灾区域按距离进行分类，可分成三类。由于其实际情况，进行应急物流配送时，可将三类归为两类进行配送。根据灾难程度分类和距离坐标聚类分析，在这两类中选取两个特征共同最明显的两个区域（汶川、理县）。故而，可以将汶川、理县两处受灾区域作为初步的应急物流服务中心点。

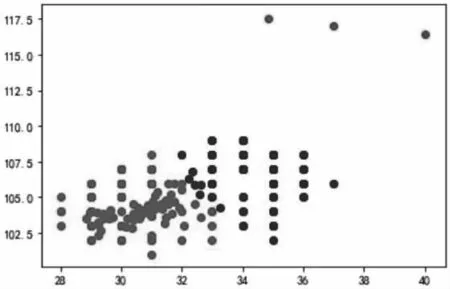
图一 受灾区域聚类分析

4.结论：

传统的应急物流服务设施选址方法很少有考虑灾情破坏程度的因素，为此本文运用聚类分析方法将不同灾害损失程度的受灾点进行分类，选取灾害损失程度较严重的受灾点作为服务设施节点[1]，为设置应急物流服务设施提供良好的决策辅助。本文希望能给研究学者提供一些理论支持。上述分析虽然对汶川地震应急物流中心的选址做了初步定位，鉴于本人的能力水平、学术经验等各方面因素，该论文仍存在一些需继续改进与完善之处。