带齿轮和液力变矩器的透平机械轴系扭振特性研究
2022-01-20冯国益
高 进, 冯国益
(东方电气集团东方汽轮机有限公司, 四川德阳 618000)
齿轮箱和液力变矩器被广泛应用于大型透平机械的启动[1]或驱动系统[2],以调节转速、功率和扭矩。
带齿轮和液力变矩器透平机械轴系扭振分析的关键是建立齿轮副和液力变矩器的扭振力学模型。齿轮副的扭振力学模型为:(1)根据齿轮副速比得到的等效模型,该模型忽略齿轮副啮合刚度[3];(2)考虑齿轮副速比和啮合刚度的传递矩阵或有限元模型[4]。液力变矩器通过液力柔性地传递扭矩, 可将其等效为一个阻尼单元[5],通过实验或性能参数计算得到阻尼单元的阻尼。
为了便于工程上利用ANSYS软件分析带齿轮和液力变矩器透平机械轴系的扭振特性,首先采用用户自定义Matrix27刚度单元模化齿轮副的扭转刚度,该Matrix27刚度单元可考虑齿轮副啮合刚度,同时采用用户自定义Matrix27阻尼单元模化液力变矩器泵轮和透平轮的连接阻尼,最后通过典型的算例验证所提出的方法,研究带齿轮和液力变矩器的透平机械轴系的扭振特性。
1 齿轮副和液力变矩器扭振力学模型
先通过齿轮副的法向接触刚度计算得到齿轮副的啮合刚度,进而可以得到齿轮副的扭转刚度,然后采用用户自定义的两节点Matrix27刚度单元模化齿轮副的扭转刚度。而液力变矩器泵轮与透平轮的连接阻尼可由液力变矩器泵轮传递到透平轮间的能量损失进行计算,然后采用用户自定义的两节点Matrix27阻尼单元模化液力变矩器泵轮与透平轮的连接阻尼。
1.1 齿轮副扭振力学模型和单元设置
1.1.1 扭振力学模型
图1为齿轮副啮合刚度模型[4],其中:K1、K2分别为齿轮1和2的法向接触刚度;r1、r2分别为齿轮节圆半径。
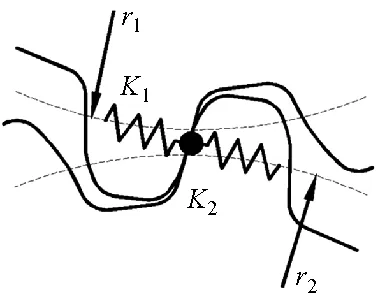
图1 齿轮副啮合刚度模型
扭转刚度矩阵的计算公式[4]为:
Ke=K1K2/(K1+K2)
(2)
式中:Kspur为扭转刚度矩阵;Ke为啮合刚度。
1.1.2 齿轮副扭振单元设置
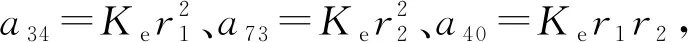
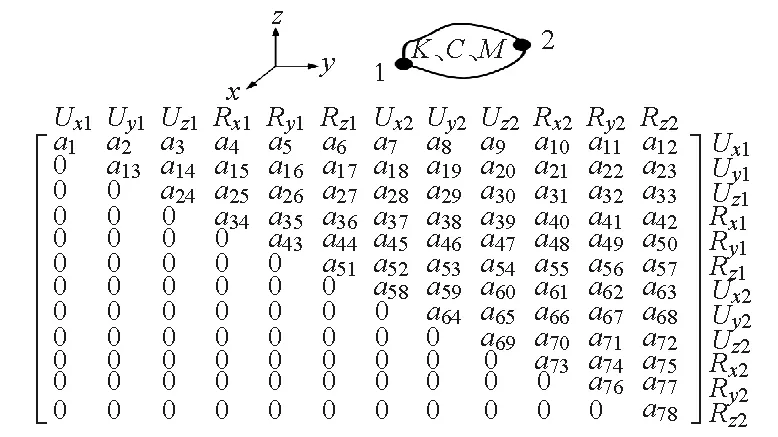
图2 Matrix27对称矩阵形式
对于有多个齿轮副的行星齿轮,太阳轮、行星轮、行星支架和齿圈的齿轮副刚度矩阵的计算公式[4]为:
式中:Kplanet为齿轮副刚度矩阵;u1~u14为矩阵中的非零元素[4]。
可将式(3)分解为6个齿轮副刚度矩阵,具体为:
(4)
图3为Matrix27非对称矩阵形式。
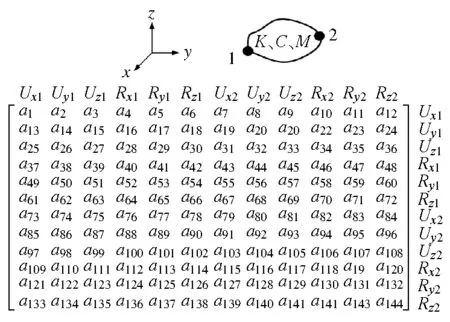
图3 Matrix27非对称矩阵形式
式(4)中6个齿轮副刚度矩阵可分别用Matrix27非对称矩阵表示。若轴线为x方向,则设置a40、a46、a112和a118分别为式(4)中扭转刚度矩阵中相应值即可。
1.2 液力变矩器扭振力学模型和单元设置
1.2.1 液力变矩器扭振力学模型
图4为某大功率液力变矩器结构示意图和力学模型,其中:JP、MP、θP分别为泵轮的转动惯量、输入扭矩、扭转角;JT、MT、θT分别为透平轮的转动惯量、输入扭矩、扭转角;CTC为液力变矩器泵轮与透平轮的连接阻尼。液力变矩器泵轮与透平轮的连接可用阻尼单元等效。
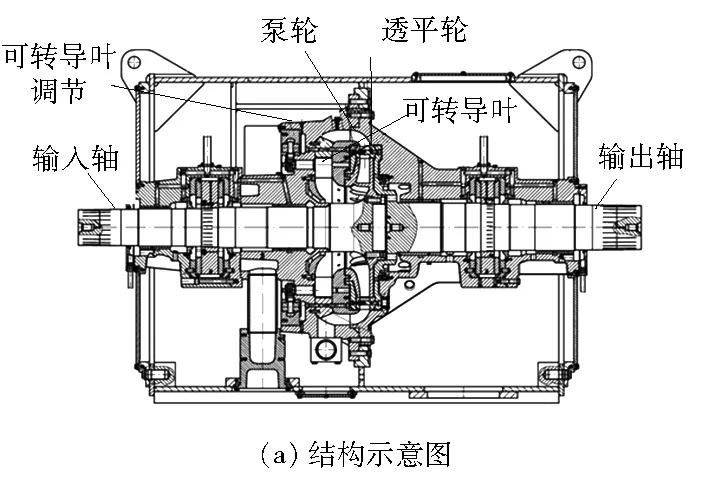
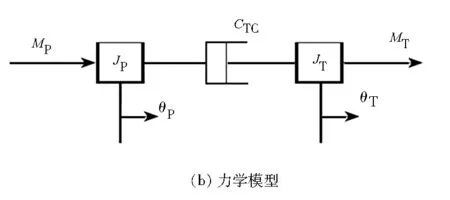
图4 大功率液力变矩器结构示意图和力学模型
CTC可由液力变矩器泵轮传递到透平轮间的能量损失进行计算,其计算公式为:
式中:PP、PT分别为泵轮和透平轮的功率;ωP、ωT分别为泵轮和透平轮的转速。
液力变矩器的阻尼矩阵C为:
1.2.2 液力变矩器扭振单元设置
在ANSYS软件中,液力变矩器阻尼单元可通过Matrix27阻尼单元进行模化。C为对称矩阵,可通过Matrix27对称矩阵表示。若轴线为x方向,则设置a34=a73=CTC,其他元素为零。
2 计算实例
2.1 平行轴齿轮轴系
图5为平行轴齿轮轴系的扭振力学模型[6],其中:J1、J2、J3、J4、J5分别为节点1、2、3、4、5的转动惯量,J1=0.248 1 kg·m2、J2=0.119 7 kg·m2、J3=0.942 0 kg·m2、J4=0.019 4 kg·m2、J5=0.089 7 kg·m2;K1-2、K2-3、K4-5分别为节点1-2、2-3和4-5轴段扭转刚度,K1-2=K2-3=1.573×105N/m,K4-5=1.180×105N/m。转动惯量用集中质量单元MASS21模化,K1-2、K2-3和K4-5用弹簧单元COMBIN14模化,节点3和节点4间为齿轮副,节点3与节点4位置齿轮的节圆半径比为3,其扭转刚度用Matrix27刚度单元模化,齿轮副啮合刚度取为1.0×106~1.0×109N/m。
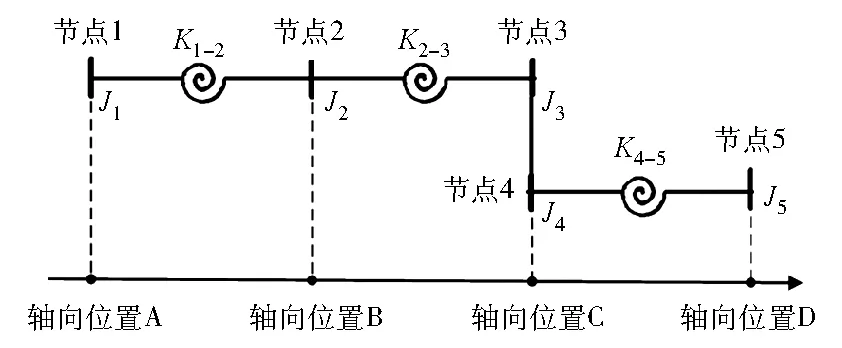
图5 简单平行轴齿轮轴系扭振力学模型
简单平行轴齿轮轴系的计算扭振频率与齿轮副啮合刚度的关系见图6。由图6可得:当齿轮副啮合刚度为1.0×109N/m时,计算得到前3阶扭振频率分别为90.5 Hz、238.2 Hz和280.6 Hz,接近不考虑齿轮副啮合刚度的前3阶扭振频率(90.5 Hz、238 Hz和281 Hz)[6]。轴系各阶扭振频率随齿轮副啮合刚度的增加而趋于定值。
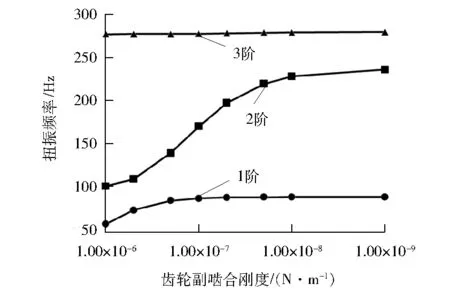
图6 平行轴齿轮轴系扭振频率计算结果
图7为简单平行轴齿轮轴系扭振归一化振型计算结果。由图7可得:轴系2阶扭振振型在齿轮副处的归一化扭转角变化量最大,所以齿轮副啮合刚度对该阶扭振频率影响最大。

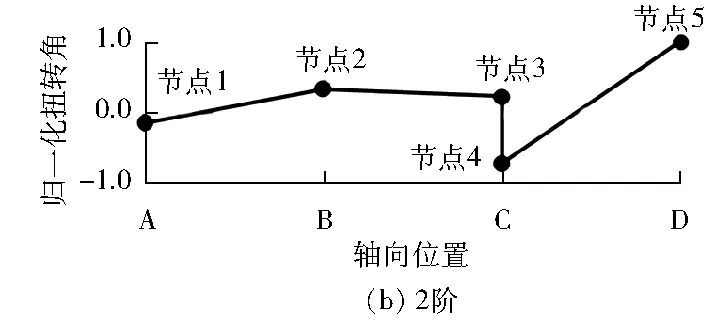
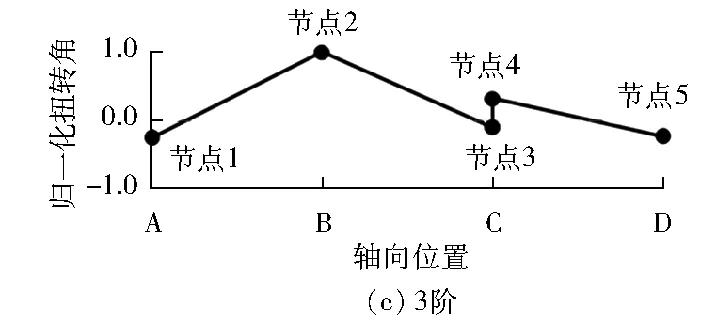
图7 简单平行轴齿轮轴系扭振振型计算结果
2.2 燃气轮机满负荷试验台轴系
燃气轮机满负荷试验台轴系由电动机、液力变矩器、齿轮箱、压气机和燃气轮机组成。该轴系中液力变矩器的阻尼根据式(5)计算,计算结果见图8,可见其阻尼随转速升高而增加。
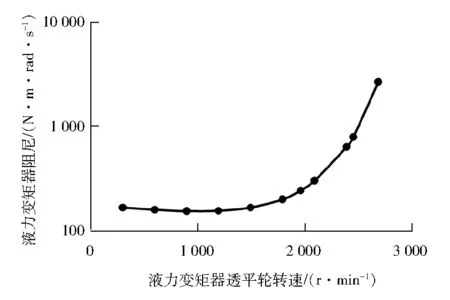
图8 燃气轮机满负荷试验台液力变矩器阻尼
燃气轮机满负荷试验台轴系扭振力学模型见图9。转子本体用梁单元Beam188模化,其中液力变矩器泵轮和透平轮的连接阻尼采用Matrix27阻尼单元模化,计算模型中阻尼取液力变矩器输出轴额定转速(2 448 r/min)时对应的阻尼(790 N·m·rad/s)。齿轮副的扭转刚度采用Matrix27 刚度单元模化,低速端和高速端齿轮副的啮合刚度分别为5.8×108N/m和4.6×108N/m。

图9 燃气轮机满负荷试验台轴系扭振力学模型
图10为计算得到轴系前4阶扭振频率和振型,其中:云图为ANSYS软件直接输出的扭振归一化振型,振型曲线为提取各个节点振型数据绘制。
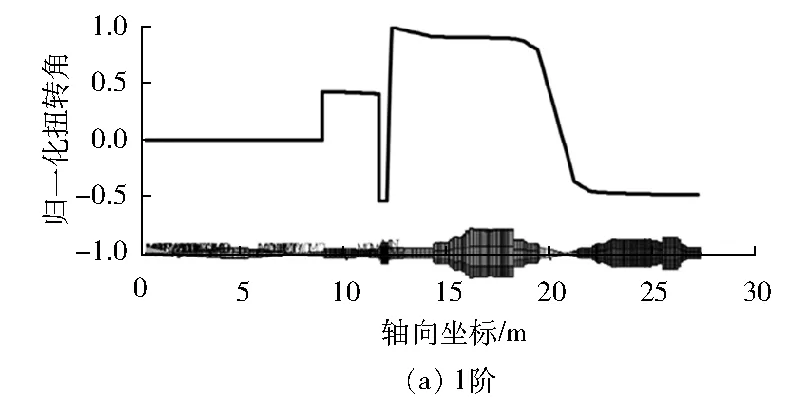
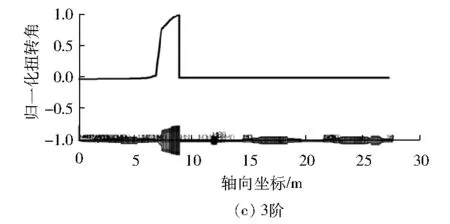
图10 燃气轮机满负荷试验台轴系扭振前4阶振型
表1为各阶扭振频率计算值和对比值,对比值是阻尼为790 N·m·rad/s时采用传递矩阵法的计算结果。
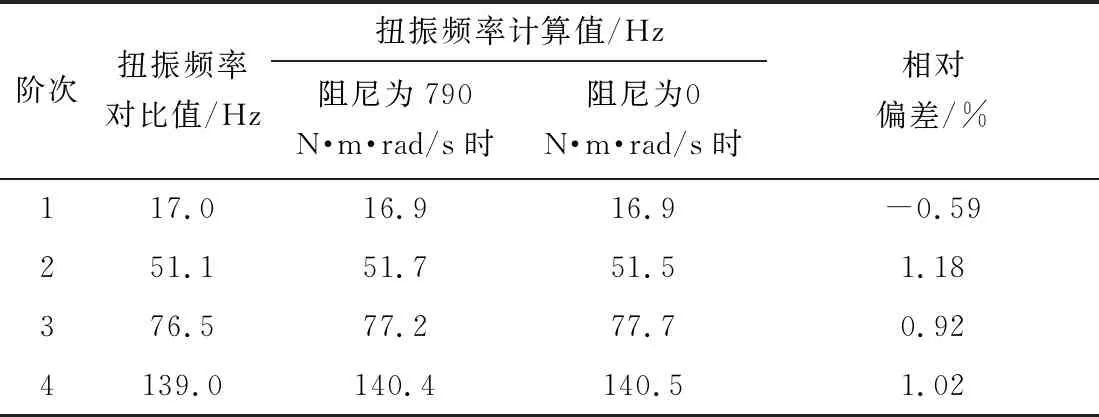
表1 各阶扭振频率计算值和对比值
由表1可得:阻尼为790 N·m·rad/s时的计算值和对比值的最大相对偏差仅为1.18%,计算结果吻合程度较高。同时,液力变矩器阻尼分别为0 N·m·rad/s和790 N·m·rad/s时,前4阶扭振频率的偏差分别为0 Hz、-0.2 Hz、0.5 Hz、0.1 Hz,说明液力变矩器阻尼对轴系扭振频率的影响较小。
轴系2阶扭振频率非常接近电动机的工频,不满足轴系扭振频率的避开率要求,需要对其扭振稳态响应进行分析,以评估轴系扭振的安全性。
在电动机轴中部施加幅值为5 749.2 N·m(10%电动机额定扭矩)、频率为45~65 Hz的激励扭矩,模态阻尼比取为0.005,计算轴系的谐响应。图11为压气机-齿轮箱间联轴器处扭矩响应。由图11可得:最大扭矩响应在压气机-齿轮箱间的弹性联轴器处,该处在51.7 Hz的扭矩响应为224.7 N·m,轴系扭振响应非常小,仅为激励扭矩的4%,这是因为液力变矩器通过液力柔性地传递扭矩,对电动机的扭振激励有很好的隔离作用。
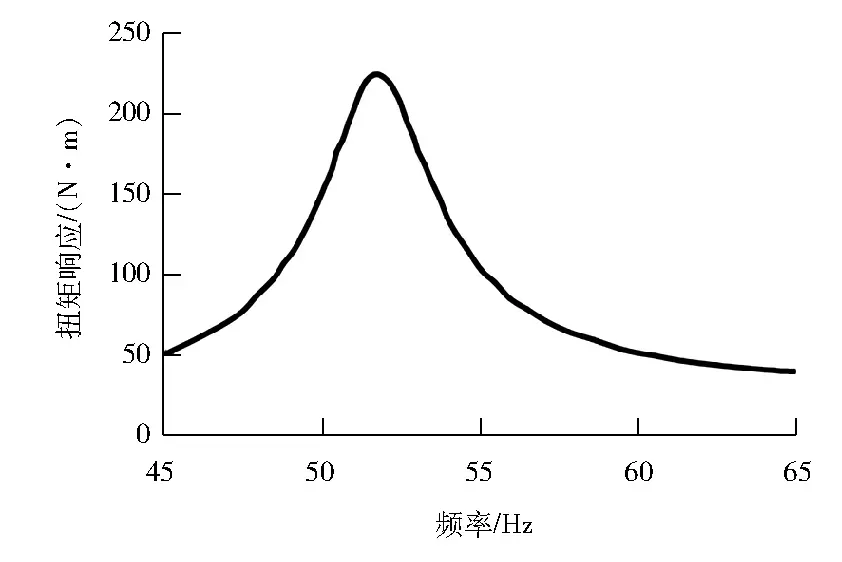
图11 压气机-齿轮箱间联轴器处扭矩响应
3 结语
分析了齿轮副和液力变矩器的扭振计算模型,给出了便于工程上利用ANSYS软件分析带齿轮及液力变矩器透平机械轴系扭振的方法,主要结论为:
(1) 齿轮副的扭转刚度可采用Matrix27刚度单元进行模化,液力变矩器泵轮和透平轮间的连接阻尼采用Matrix27阻尼单元进行模化。
(2) 轴系各阶扭振频率随齿轮副啮合刚度的增加而趋于定值。
(3) 液力变矩器泵轮与透平轮的连接阻尼对轴系扭振频率影响很小,说明液力变矩器对轴系扭振激励有很好的隔离作用。
