求解最小包容球问题的一类光滑逼近算法

李 尧， 蒋 毅*， 柏雪婷

（1.四川师范大学 数学科学学院，四川 成都 610066；2.四川师范大学 可视化计算与虚拟现实四川省重点实验室，四川 成都 610066）

在Rn空间中，令闭集合

Bi∶＝｛x∈Rn：‖x-ci‖≤ri，i ＝1，2，…，m｝，它是以ci为球心，ri≥0 为半径的球.给定一组球

最小包容球问题是找一个能够包容B 中m个球且半径最小的球，简称SEB 问题.该问题可以表述为非光滑凸优化问题

由于函数f（x）是严格凸的，所以问题（1）的解存在且是唯一的.

最小包容球问题应用于位置分析、军事行动等方面，它本身也是计算几何学中的一个有趣的问题［1-5］.当维数n≤30 时，文献［5-7］中的方法在理论和数值实验中都能得到令人满意的结果；然而，这些方法在处理维数n ＞30 时的效率比较低下.

近年来，许多学者考虑n ≥100 的情况.Pan等［8］首先将具有一定组合性质的问题（1）转化为一个包含极大值函数φ（t）＝max｛0，t｝的确定非光滑问题，然后使用CHKS 光滑函数［9-10］来逼近φ（t），由此建立了一个全局收敛的拟牛顿算法.Zhou等［11］利用对数指数光滑逼近［12］的思想提出了一种有效求解最小包容球问题的算法.基于此类方法的启发，本文提出了一类光滑逼近算法.

在本文中所有向量都是列向量.设Id表示d ×d单位矩阵，co（S）是集合S⊆Rn的凸包.对于凸函数f：Rn→R，∂f（x）表示f在x处的次微分.

1 光滑逼近

首先，问题（1）中的f（x）可由线性优化问题重新定义如下：

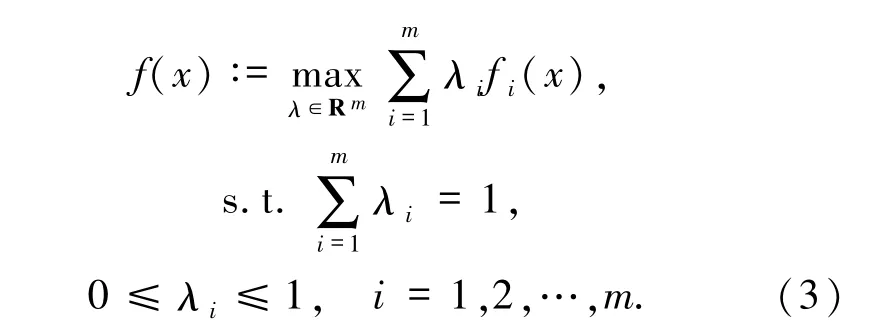
问题（3）满足强对偶定理，对于任意x∈Rn，其最优值与对偶线性规划的最优值相同.因此，有

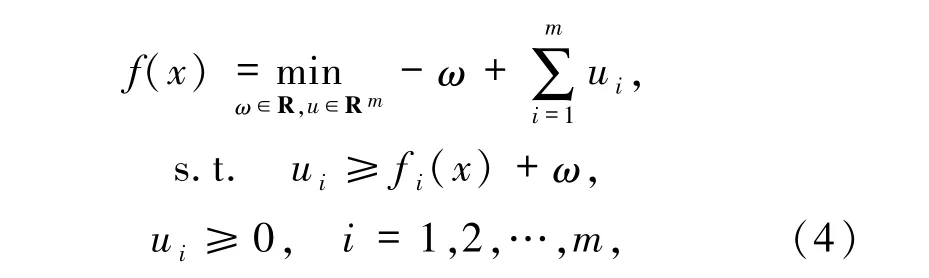
其中，ω和ui是与约束和λi≤1（i ＝1，2，…，m）相关的拉格朗日乘子.由于

且ui≥0，令

将上式代入（4）式的目标函数，消除变量u，可以得到

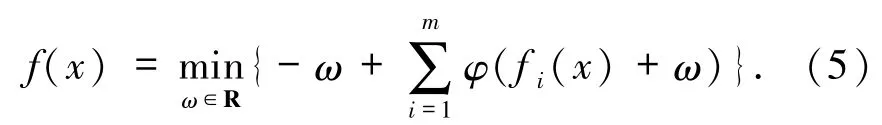
因此，原问题（1）转化为了非光滑优化问题，具体如下：

因为φ（fi（x）+ω）是不可微的，所以本文利用光滑函数对其进行逼近.应用的光滑函数如下：

文献［13-14］证明函数φ（t；p）满足如下性质.

引理1.1对任意p∈（0，1］，函数

满足：

（i）φ（t；p）是严格凸的可微函数，且

根据光滑函数φ（t；p），定义如下函数

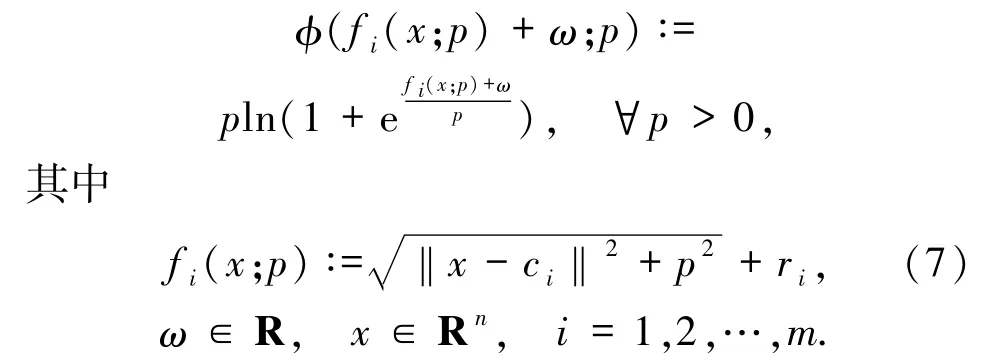
下面考虑光滑无约束优化问题

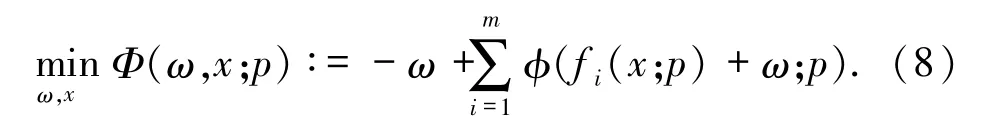
首先，证明函数Φ（ω，x；p）的相关性质.

引理1.2问题（8）中定义的函数Φ（ω，x；p）具有以下性质：

（a）对任意ω∈R，x∈Rn和0 ＜p1＜p2，则

（b）对任意ω∈R，x∈Rn和p ＞0，则

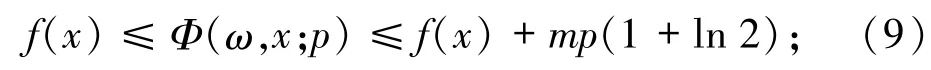
（c）对任意p ＞0，Φ（ω，x；p）是连续可微且严格凸的.

证明（a）对任意p ＞0，t∈R，有

又因为fi（x；p）随p 严格增加，对于任何0 ＜p1＜p2，则有

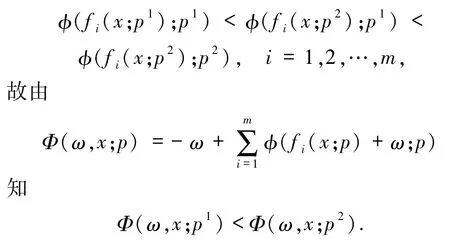
（b）经过简单的计算，可以得到

对任意ω∈R，x∈Rn和p ＞0，由上述等式可推出如下不等式关系成立：

上述2 个不等式相加，可以得到

又根据Φ（ω，x；p）的定义得

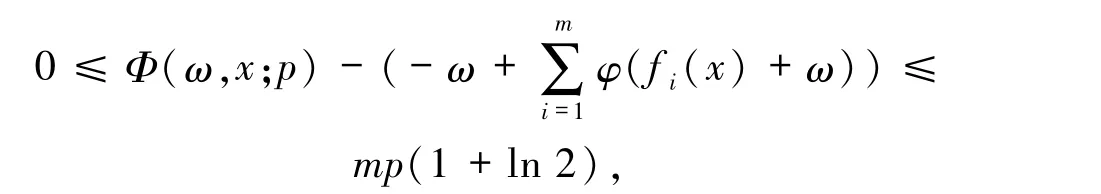
故不等式

成立.

（c）对任何p ＞0，显然Φ（ω，x；p）是连续可微的.下面证明Φ（ω，x；p）是严格凸的，由（8）式可得

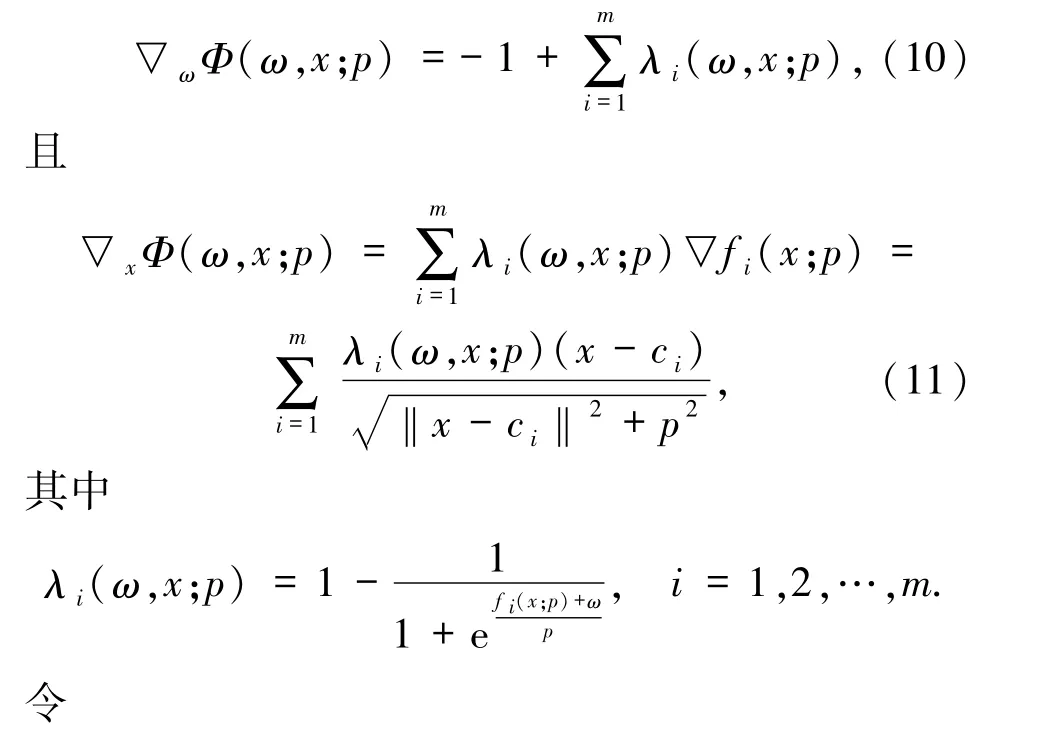
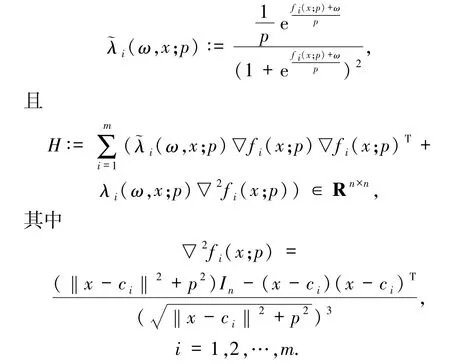
由（10）和（11）式得

其中第一个不等式是由λi（ω，x；p）的非负性和▽2fi（x；p）的表达式得到的，第二个不等式是由Cauchy-Schwartz不等式得到的.这表明对任意p ＞0，Φ（ω，x；p）是ω和x的联合严格凸函数.

2 光滑逼近算法

由引理1.1 和1.2 可知问题（8）是问题（6）的光滑逼近.因此，给出如下光滑逼近算法.

算法A步骤1令σ∈（0，1），（ω0，x0）∈R×Rn，∊1，∊2＞0 和p0＞0.

步骤2k 取值0，1，2，…，序列（wk，xk）按如下方式产生：使用有限内存BFGS 算法求解光滑无约束优化问题

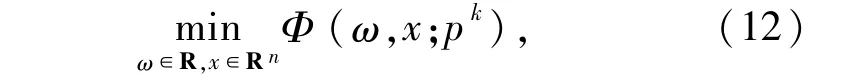
得到相应的最优解记为（ωk，xk），且满足

步骤3若pk≤∊1，则停止计算，输出（ωk，xk）；否则，转步骤4.

步骤4令pk+1＝σpk，更新k ∶＝k+1，转步骤2.

算法A采用有限内存BFGS方法求解问题（12），它能有效地求解维数较大的最小包容球问题.接下来，将证明算法A的收敛性以及求出的最优解就是问题（1）的最优解.

引理2.1设｛ωk，xk｝k≥1为算法A 产生的点序列，则｛xk｝k≥1的极限点为问题（1）的最优解.

证明设｛ω*，x*｝为｛ωk，xk｝的极限点，并假设当k→+∞时，｛ωk，xk｝→｛ω*，x*｝.由于｛ωk，xk｝是问题（12）的解，则

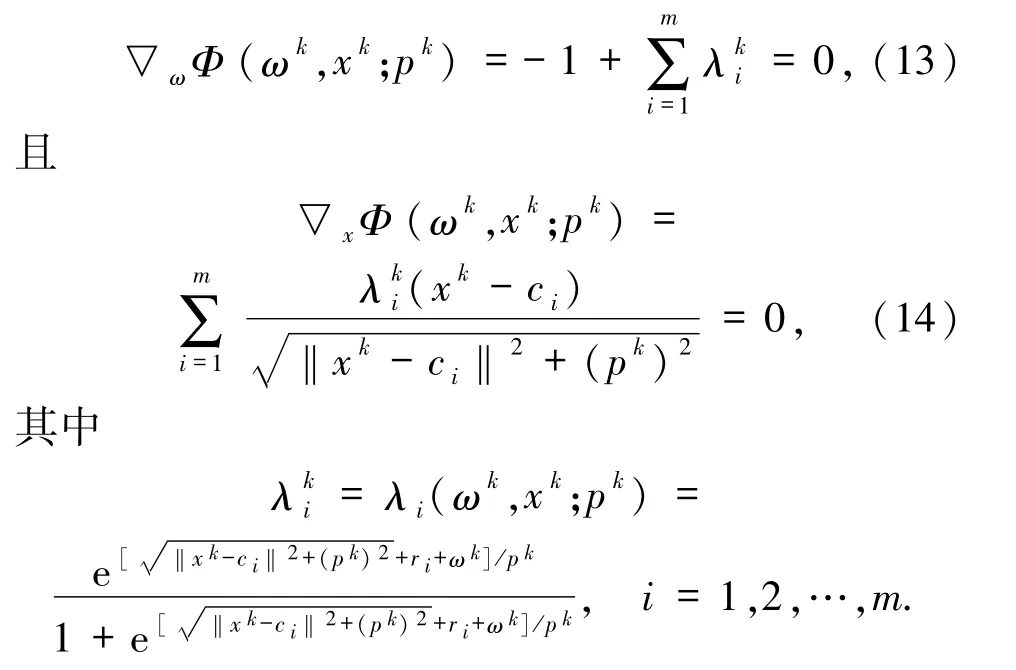
此外，由（1）和（6）式，可以推断出

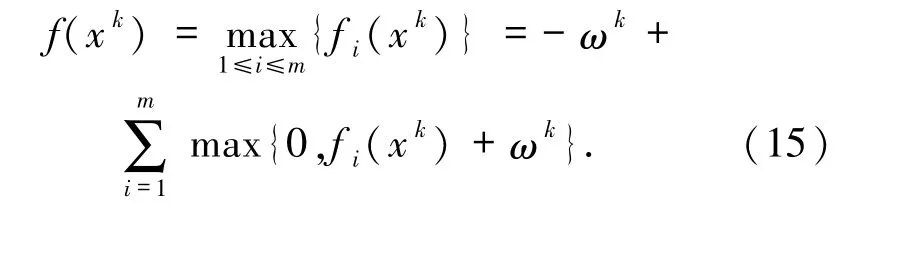
定义指标集如下：

由（15）式，fi（x）和max｛0，t｝的连续性，可以得到

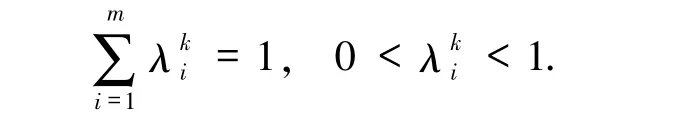
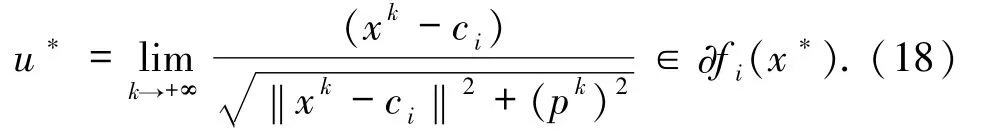
由（14）式可以得到

则（18）和（19）式表明

0∈co｛∂fi（x*），i∈I（x*）｝＝∂f（x*）.从而，x*是问题（1）的最优解.因此，要完成引理2.1的证明，只需要证明（20）式成立.

首先，由（17）式可以很容易地推断出

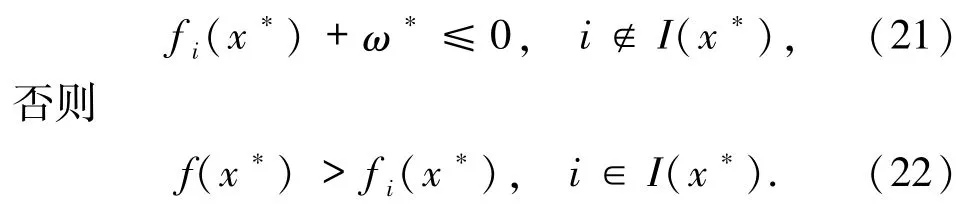
现在，分别考虑|I（x*）| ＝1 和|I（x*）| ＞1 的情况，其中| I（x*）|表示集合I（x*）中的元素个数.

情形1如果|I（x*）| ＝1，则假设

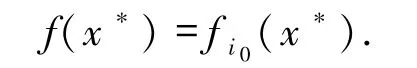
由（21）式可以推断出，对于足够大的k，有

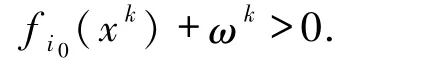
结合λi（ωk，xk；pk）的定义有

又由（13）式可以得到

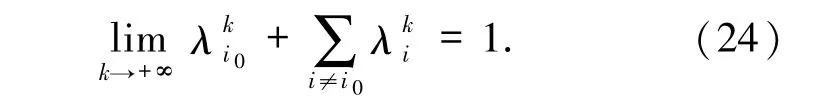
由（23）和（24）式可以得到（20）式成立.

情形2如果|I（x*）| ＞1，则很容易证明（21）式严格成立，即

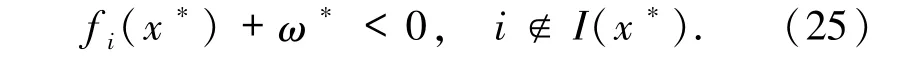
否则，一方面有

另一方面，（17）式表明

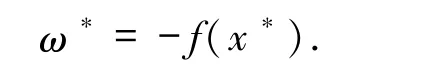
它表明（20）式成立.因此，引理2.1 的证明完成.

定理2.2设｛xk｝为算法A产生的点序列，如果x*是问题（1）的唯一最优解，则

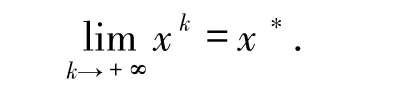
证明对于任何k≥1，通过引理1.2 和算法A，可以看出

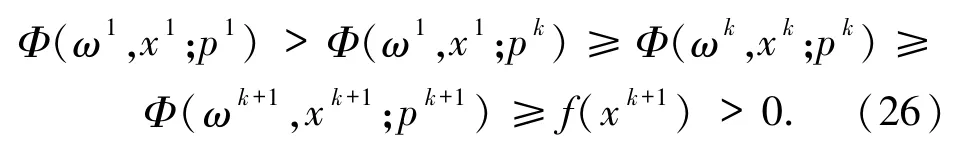
由f（x）是强制的，可知水平集

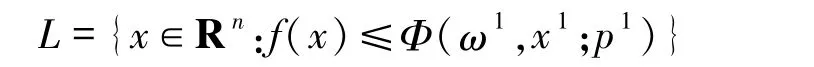
是有界的.结合（26）式，有｛xk｝⊂L.因此，｛xk｝在Rn中有界.如果x*是问题（1）的唯一最优解，则引理2.1 表明

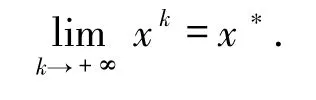
3 数值实验

下面给出数值实验结果.使用Core i7 2.4 GHz个人电脑，在Matlab 环境下，运用算法A 和文献［8］中的算法求解最小包容球问题.算法中的参数定义如下：

采用文献［8］的随机序列

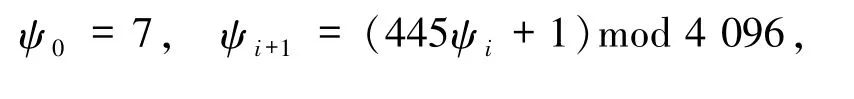
球的半径ri和球心ci（i ＝1，2，…，m）依次设置为，…，顺序如下：

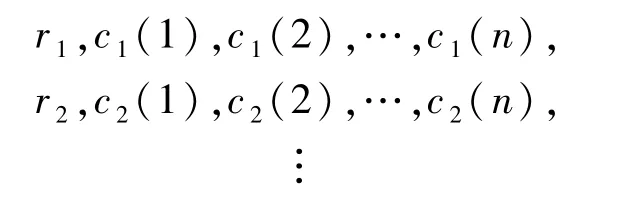
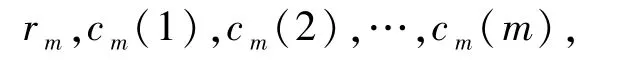
初始点设为ω0＝0 和x0＝0.

数值结果汇总在表1 和表2 中，欧几里德空间的维数和球的个数分别用n 和m 表示，平均CPU时间用时间（单位：s）表示，平均迭代次数用迭代次数（单位：次）表示.

表1 n固定时，算法A与文献［8］中算法的比较Tab.1 Performances of Algorithm A and that used in reference［8］with fixedn

表2 m固定时，算法A与文献［8］中算法的比较Tab.2 Performances of Algorithm A and that used in reference［8］with fixedm

对于每对（m，n），用437、441、445、449 和453代替整数445，对（27）式中产生的5 组数据分别运行本文的算法.表1 和表2 中的结果均取平均数.当球的个数m 增加时，本文所给算法A 的平均CPU时间比文献［8］中的算法快的优势越明显，并且当维数n增加时，算法A具有同样的优势.

与文献［8］中算法相比，算法A有2 个优点：一是在处理的数据逐渐增大时，算法A具有计算的速度优势；二是它的迭代次数比文献［8］中的算法要少.因此，本文所给的算法A 对于求解最小包容球问题是有效的.