基于消费强度分析的钢材需求预测

□ 刘光明

一、引言

钢铁工业是国民经济的基础工业，其生产和消费与国民经济发展密切相关。当前，我国经济发展已经从高速发展阶段步入高质量发展阶段，在“双碳”目标约束下，钢铁行业也将进入减量提质阶段。因此，为更好地研究新常态下钢材需求变化，除了要研究宏观经济发展变化的影响外，更要对钢材消费强度进行分析。

黄永强等（2007）结合我国钢材消费强度变化及原因的定性分析，预计未来的钢材消费强度情况，并据此对钢材需求进行了预测[1]。张群、张超等（2011）基于派生需求理论，构建了钢材消费强度的超越对数模型，通过模型发现GDP对钢材消费的拉动作用呈现减弱的趋势[2]。瞿云华、张焕成等（2016）构建了钢材消费强度的曲线拟合模型、时间序列模型和灰色预测模型，并以2005—2014年的钢材消费强度数据为样本，对2015—2020年的钢材消费强度进行了预测[3]。陈程、管志杰等（2019）结合近年来国内生产总值、固定资产投资与钢材消费量之间的系数关系，对2025年钢材需求量进行了预测[4]。

本文以1982—2011年的钢材消费数据为样本，建立钢材消费强度预测的ARIMA模型和多元回归模型，并基于2012—2020年的数据为测试样本对模型进行评估和比较，选择较优模型对“十四五”时期的钢材消费强度进行估计，进而对我国钢材表观消费量进行预测。

二、模型建立与分析

1.钢材消费强度

本文中的钢材消费强度指的是单位GDP的钢材消费量，定义如下：

式（1）中IUt为钢材消费强度，Dt为钢材表观消费量，GDPt为国内生产总值，t表示年份。其中，钢材表观消费量数据来源于世界钢铁统计年鉴，GDP来源于国家统计局网站数据。根据式（1）计算得到近年来我国钢材消费强度情况如图1所示。

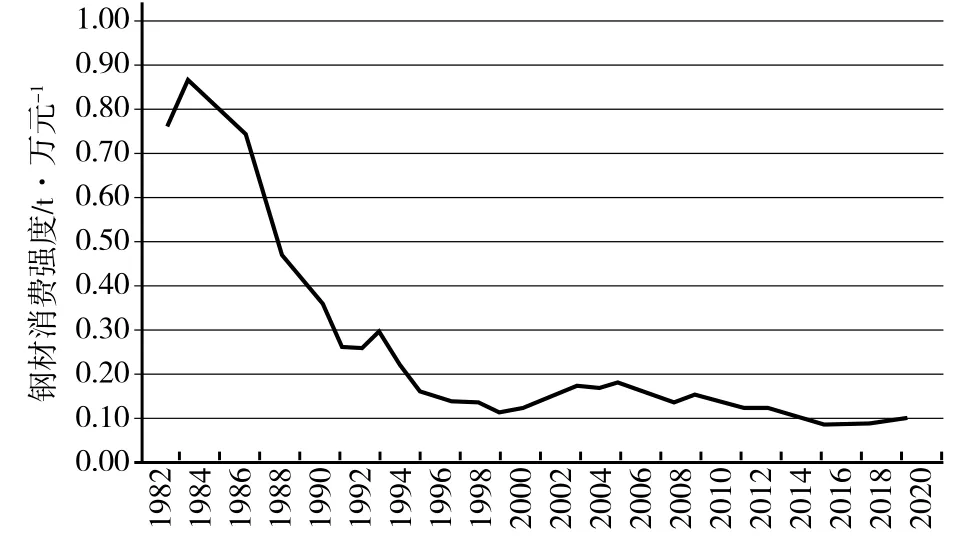
图1 近年来我国钢材消费强度变化

2.ARIMA模型

（1）数据准备

本文以1982—2020年的钢材表观消费和国内生产总值（GDP）数据计算得到钢材消费强度序列数据，在本文中以y表示。其中以1982—2011年的数据为训练样本进行模型拟合，以2012—2020年的数据为测试样本进行模型评估。

（2）模型识别和定阶

从近年来我国钢材消费强度变化可以看出，钢材消费强度序列存在着明显的下降趋势，为非平稳的时间序列。因此，本文通过差分处理来消除序列的不平稳性，并通过ADF单位根检验进行判断，结果如表1所示。

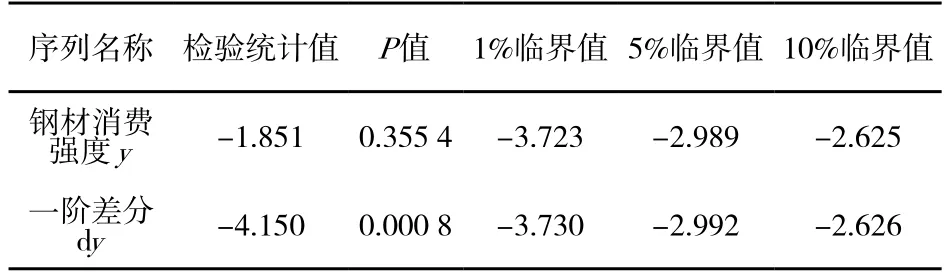
表1 ADF单位根检验结果

可见，一次差分后的序列dy的检验统计值都小于各临界值，且P=0.0008﹤0.05，因此拒绝原假设，即不存在单位根，序列为平稳时间序列。因此，模型中差分的阶数d=1。

对于模型参数自回归项数p、滑动平均项数q，可以通过观察自相关和偏自相关图确定，也可利用信息准则函数法来确定，本文选择根据不同参数组合的AIC值来选择最优的模型参数。其计算结果如表2所示，可以看到模型ARIMA(1,1,1)的AIC和BIC值最小，因此p=1、q=1、d=1为ARIMA模型最优参数。

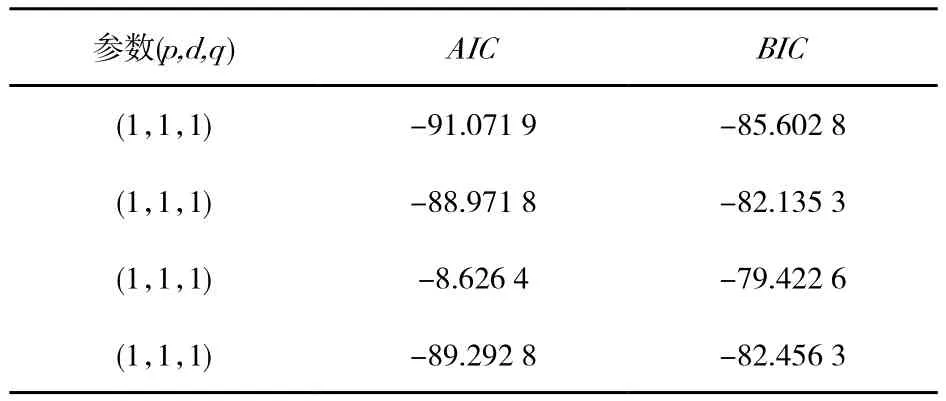
表2 不同参数组合的AIC值比较

（3）模型预测

通过对模型预测结果进行差分还原，得到测试区间2012—2020年的钢材消费强度预测数据，并与实际测试样本数据进行对比（见图2）。可以看出，模型整体预测效果较好；同时，ARIMA模型短期预测效果较好，随着预测时间周期的加长，预测效果也逐步下降。

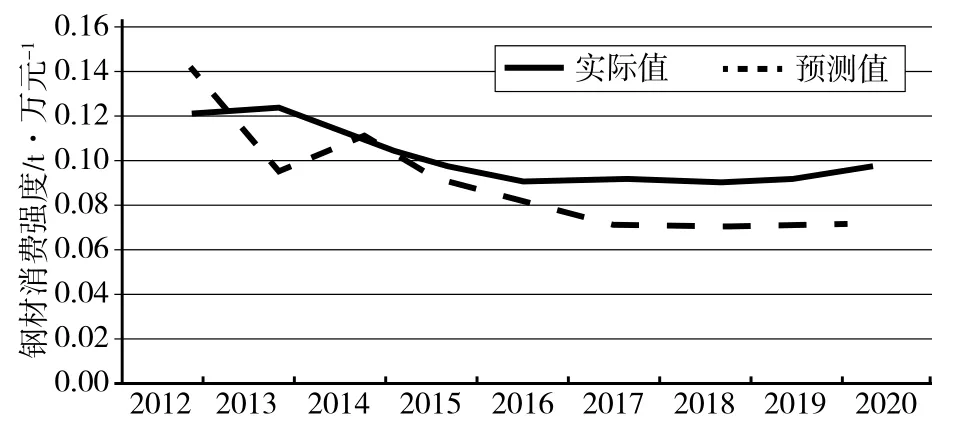
图2 ARMA模型预测效果评估

3.多元回归模型

（1）数据准备

本文选择了人均GDP、城市化水平和第三产业占比分别作为自变量x1、x2、x3，探究其对钢材消费强度的影响，同样以钢材消费强度作为因变量y。在分析预测前，本文对指标数据进行取对数处理，这样做一方面可以减少指标数据量纲的影响，另一方面可以使得线性趋势更加明显。

（2）相关性分析

分别绘制因变量和各自变量的散点图并计算其相关系数，对数处理后序列相关图见图3。可见，钢材消费强度与各变量之间存在着较强的相关关系，可以通过建立回归模型进行分析预测。

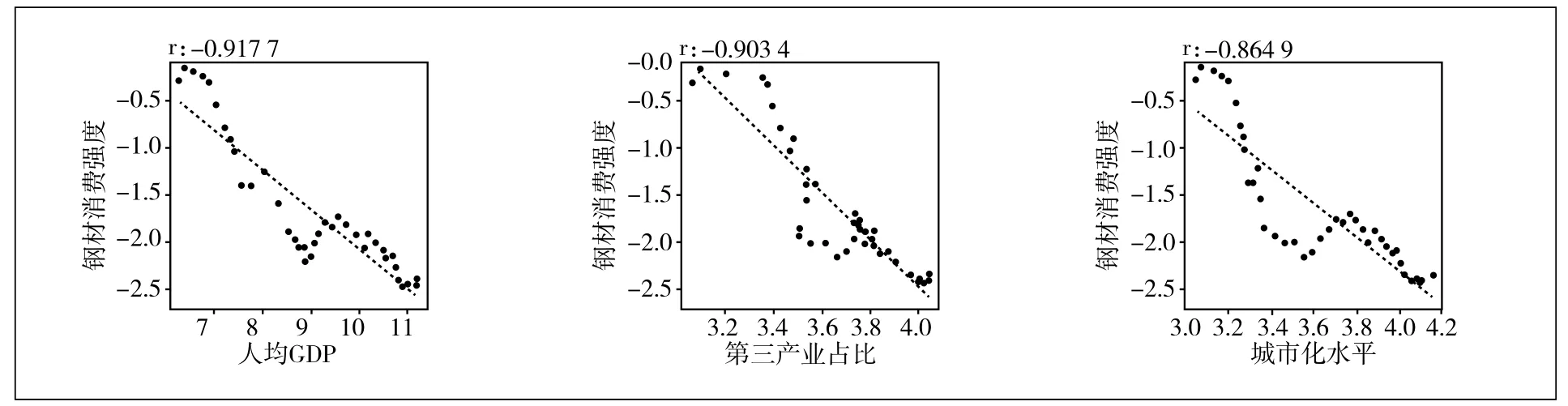
图3 钢材消费强度与各自变量的散点示意

（3）模型建立与分析

本文利用1982—2011年的样本数据，通过统计分析软件对相关数据进行回归分析，回归分析结果分别见表3和表4。

表3 回归结果统计

表4 回归分析

回归分析结果表明，人均GDP、第三产业占比、城市化水平对钢材消费强度存在显著的影响，回归方程总体显著，且拟合效果较好。因此，确定的回归模型为：

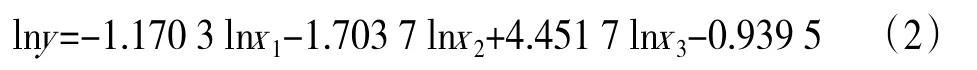
式（2）中，lny为钢材消费强度的对数；lnx1、lnx2、lnx3分别为人均GDP、第三产业占比和城市化水平的自然对数。

（4）模型预测

通过对模型预测结果进行指数运算还原，得到测试区间2012—2020年的钢材消费强度预测数据，并与实际测试样本数据进行对比（见图4）。可以看出，模型整体预测效果较好。

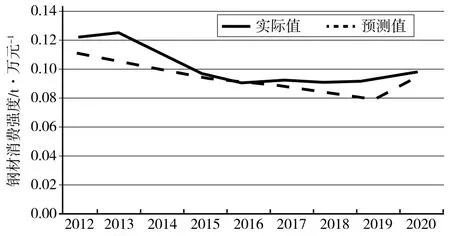
图4 多元回归模型预测效果

4.模型比较

本文建立了钢材消费强度预测的时间序列ARIMA模型和多元回归模型，其预测效果比较如下：从图5可以直观看出，回归模型的整体预测效果要优于ARIMA模型；从评估指标看，ARIMA模型和回归模型的平均绝对误差（MAE）分别为0.0169和0.0086，均方根误差（RMSE）分别为0.0189和0.0104，回归模型的评估指标要优于ARIMA模型。因此，回归模型对钢材消费强度的预测效果较好。

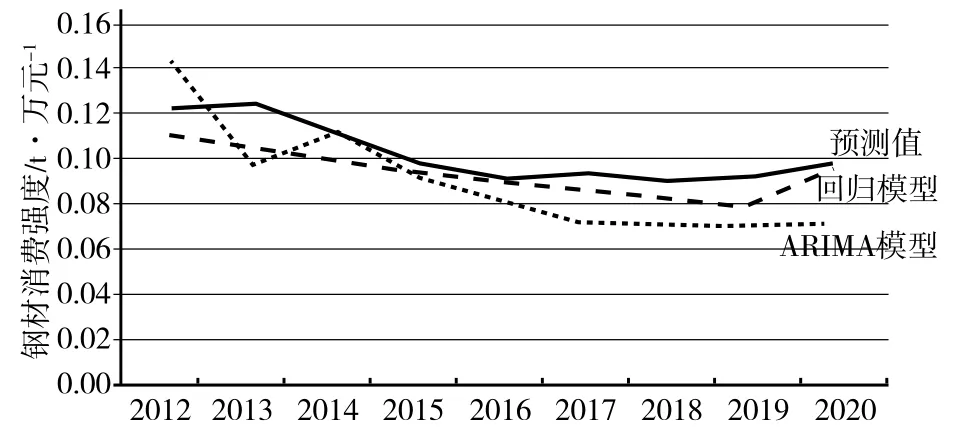
图5 模型预测效果比较

三、钢材需求预测

通过上述分析，本文选择回归模型对钢材消费强度进行预测，进而实现对钢材需求的预测。

首先，结合权威结构预测数据对自变量值进行估计，按照国际货币基金组织的预测，中国2021年经济增速在8.4%左右、2022年在5.6%左右，假设2022—2025年保持5.6%的增长速度，到2025年我国GDP约1369497.72亿元。另外，根据联合国发布的2025年人口预测数据，可估算出我国人均GDP将达到91000元左右。

中国社会科学院农村发展研究所、中国社会科学出版社联合发布的《中国农村发展报告2020》（以下简称“报告”）预计，到2025年中国城镇化率将达65.5%。随着我国经济步入高质量发展阶段，我国经济结构将继续优化，预计未来第三产业占比将保持平稳增长，到2025年将达到60%左右。

基于以上数据，根据模型估算2025年我国钢材消费强度约为0.07，钢材表观消费量将在96000万吨左右。

四、结论与建议

本文建立了钢材消费强度预测的ARIMA模型和多元回归模型，在此基础上选择了较优模型对2025年钢材消费强度进行了估计，进而实现了对钢材消费量的预测。可以看到，随着我国经济步入高质量发展阶段，产业结构持续优化，城市化进程加快，我国钢材消费强度将趋于下降。根据模型预测结果，到2025年我国钢材消费强度约为0.07，钢材表观消费量将在96000万吨左右。

可以预见，未来中国钢材需求总量虽然保持高位，但与目前相比存在下降的趋势，钢铁行业发展将从数量增长转向质量提升阶段。面对这一趋势，建议钢铁企业转变发展思路，加快产品升级和结构调整，适应新发展阶段市场需求变化，助推钢铁行业高质量发展。