基于曲轴轮廓误差分析的随动磨床轴性能预测*

房小艳 盛晓伟 孙以泽

(①东华大学机械工程学院，上海 201620；②上海机床厂有限公司上海磨床研究所，上海 200093)

曲轴是汽车发动机的关键部件，其加工质量直接影响发动机的性能和可靠性，因此曲轴加工在汽车工业中起着重要的作用。在大规模汽车发动机曲轴生产线上，为了满足加工精度和效率要求，数控曲轴随动磨床已被广泛使用[1-2]。曲轴随动磨削是通过控制工件的回转轴(C轴)和砂轮的横向进给轴(X轴)即C-X两轴联动的方式保持砂轮外圆和曲轴连杆颈始终相切[3-6]。随动磨削方法比需要适当夹具和反复调整回转中心的传统磨削方法具有更高的加工效率，更高的柔性和更高的精度[1]。依据随动磨削工艺的特点，曲轴轮廓误差中包括随动磨床C轴和X轴的位置控制误差信息，而曲轴轮廓误差又是曲轴生产现场随机抽检最直观的数据。因此，如果能够找出曲轴轮廓误差和随动磨床C轴、X轴位置控制误差之间的对应关系，就能够通过曲轴轮廓误差分析去预测随动磨床C轴和X轴的性能，对于曲轴随动磨床的可靠性维护具有重要意义。

曲轴轮廓误差中蕴含着随动磨床的性能信息，砂轮的状态信息和曲轴材料的特征信息[7]。传统的轮廓误差信号分析方法大多以积分变换为基础，如傅里叶变换、小波变换等，需要根据轮廓误差信号特征人工设计选择合适的基函数，匹配信号特征分量。积分变换方法对人工先验知识依赖性较强，在分析处理实际的复杂多变信号时缺少自由度和自适应性，难以同时兼顾并有效提取信号中的各种变化特征。自从Huang N E等提出经验模态分解(empirical mode decomposition, EMD)方法[8]和集总经验模态分解(ensemble empirical mode decomposition, EEMD)方法[9]以来，吸引了众多学者的关注。近年来出现了多种新的信号分解方法，比如局部均值分解(local mean decomposition, LMD)方法[10]、本质时间尺度分解(intrinsic time-scale decomposition, ITD)方法[11]、经验小波变换(empirical wavelet transform, EWT)方法[12]、变分模态分解(variational mode decomposition, VMD)方法[13]和自适应局部迭代滤波(adaptive local iterative filtering, ALIT)方法[14]等。以上信号分解方法无需根据先验知识设计基函数，分解是后验的，完全由数据驱动，对信号变化具有自适应能力，因此该类分解方法统称为自适应模态分解方法。各种自适应模态分解方法各有优劣，适用于不同类型的复杂信号分解。本文作者在文献[7]中提出基于EEMD的曲轴轮廓误差分析方法，虽然该方法可以分解出与随动磨床C轴和X轴相对应的分量，但是无论在方便性、快速性还是分解质量上都与本文提出的方法有所差距。

本文首先给出由随动磨床轴位置控制误差计算曲轴轮廓误差的方法。其次提出基于VMD的曲轴轮廓误差分析方法。最后采用提出的计算和分析方法，找出曲轴轮廓误差与随动磨床C轴和X轴位置控制误差之间的对应关系，从而实现由曲轴轮廓误差分析对随动磨床轴性能的预测。

1 由轴位置控制误差计算曲轴轮廓误差的方法

曲轴随动磨床结构简图及所研究误差数据来源如图1所示，曲轴磨削后可测量曲轴各连杆颈的轮廓误差。曲轴随动磨床的数控系统具有跟踪功能，可实时采集C轴和X轴的位置控制误差。

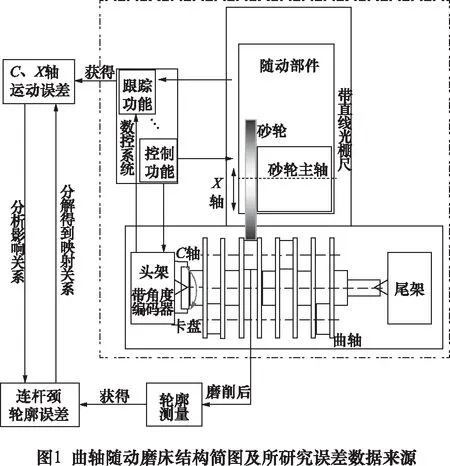
在随动磨削过程中，砂轮总是与曲轴连杆颈相切，曲轴连杆颈的轮廓是由砂轮的往复运动跟随曲轴的回转运动形成的[7]。在理想情况下，曲轴连杆颈的轮廓是一个标准的圆，此时随动磨床的C轴和X轴满足磨削运动理论控制方程。然而，在实际加工中，C轴和X轴的运动控制均有误差，因此，实际磨削得到的曲轴连杆颈并不是一个标准的圆。对实际加工得到的曲轴连杆颈轮廓采用最小二乘拟合可以获得基圆，实际轮廓和基圆的差就是轮廓误差[7]。在位置控制中，实际值和理论值的偏差是不可避免的，因此，导致曲轴连杆颈轮廓误差的主要根源就是C轴和X轴的位置控制误差。由C轴和X轴位置控制误差计算曲轴轮廓误差的过程如图2所示。

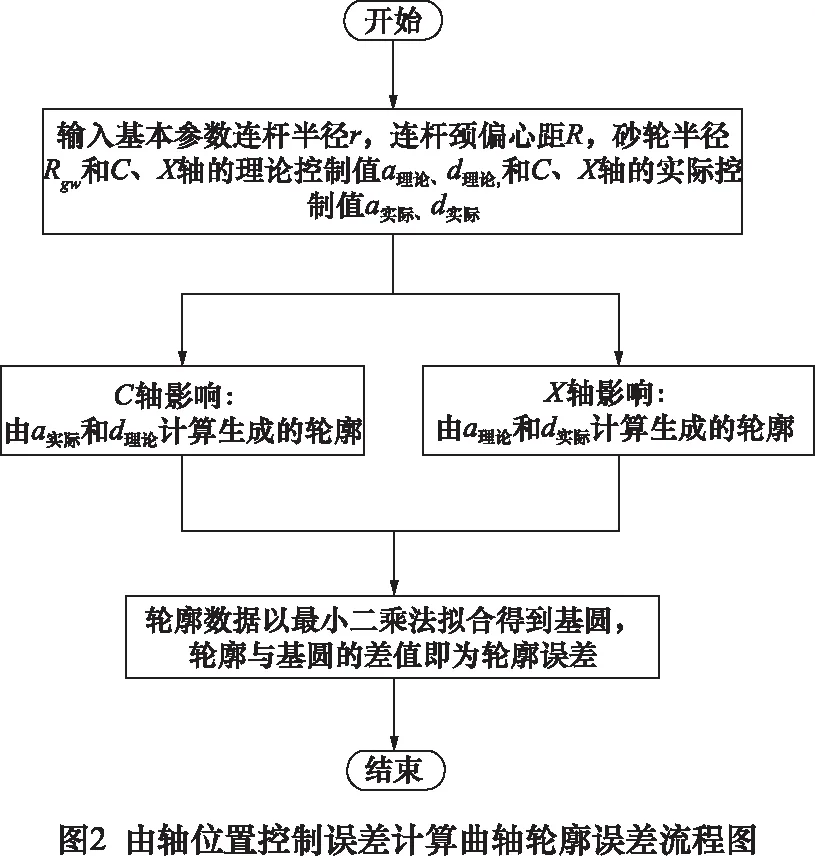
2 基于VMD的曲轴轮廓误差分析方法

VMD方法是一种非递归分解方法，它能够自适应得将复杂多分量信号分解为调幅-调频分量，而且对噪声稳定[13]。VMD将分解后的本证模态函数(intrinsic mode functions, IMFs)定义为解析的调幅-调频模型，将调幅-调频模型参数与IMF带宽关联。根据IMF的窄带性质，通过带宽最小化求解调幅-调频参数，从而获得IMF。同其他自适应模态分解方法相比，VMD具有严密的数学理论基础支持[15]。当使用VMD方法分解信号时，约束变分优化问题为：

(2)

式中：uk(t) 为第k个IMF；ωk为对应的中心频率；K为分解的数目；x(t)为待分解信号。

为了将式(2)的约束变分优化问题转化为无约束问题，需要引入二次惩罚因子α和Lagrange乘子λ，以便快速收敛并增强约束。通过引进这两个参数，增广的Lagrange表达式如下所示：

L[{uk(t)},{ωk},λ(t)]

式中：〈,〉表示内积。

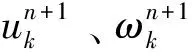
VMD的完整算法如下：

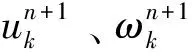
(4)

(5)

λn+1=λn+

(6)

(3) 检查收敛条件：

(7)

式中：ε为收敛终止条件，如果满足条件，则停止分解，否则令n=n+1，返回步骤(2)。

3 磨削实验及误差数据分析结果

3.1 磨削实验

一台数控随动磨床用来加工曲轴连杆颈，该机床型号是上海机床厂有限公司研制的H405-BF数控曲轴随动磨床，磨削实验布局如图3所示。数控系统是西门子840D，在曲轴磨削过程中，使用具有跟踪功能的数控系统实时采集C轴和X轴的位置控制误差。磨削完成后，测量曲轴连杆颈的轮廓误差，如图4所示。磨削采用CBN砂轮，砂轮半径299.970 mm。磨削曲轴是来自上汽通用LTG发动机生产线，连杆颈直径48.040 mm，偏心距49.000 mm[7]。

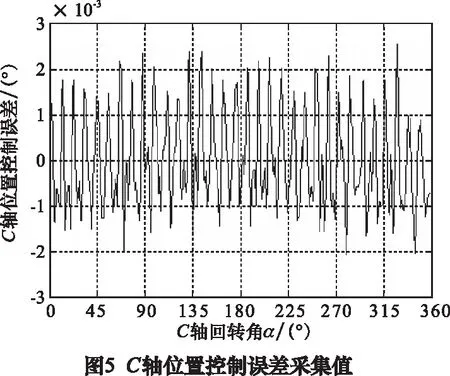
C轴和X轴位置控制误差的采样周期是4 ms，采集结果如图5和图6所示。曲轴磨削后，使用ADCOLE 1200SH综合测量仪测量曲轴连杆颈轮廓误差，测量数据经过截止频率为50 UPR的高斯滤波，轮廓一周360°，测量1 440个点，测量结果如图7所示。

3.2 由轴位置控制误差计算曲轴轮廓误差的结果

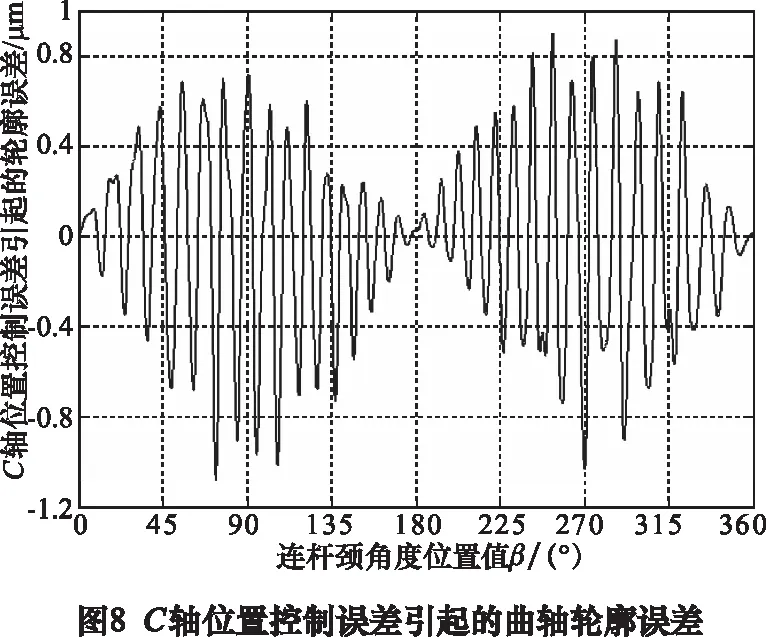
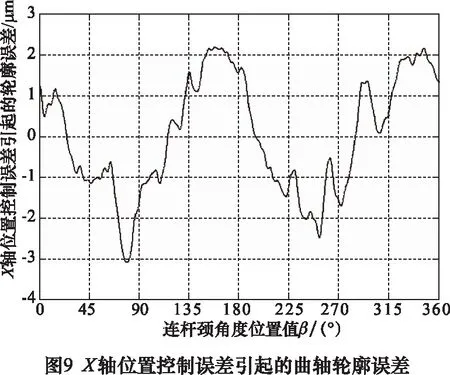
忽略数控曲轴随动磨床砂轮架、砂轮和砂轮主轴的变形，C轴和X轴的位置控制信息等价于砂轮中心的轨迹信息。由于在测量曲轴连杆颈轮廓误差时，使用了截止频率为50 UPR的高斯滤波，因此在由轴位置控制误差计算曲轴轮廓误差时，为具更好的可比性，使用了相同的滤波处理。按照图2方法计算的由C轴位置控制误差和X轴位置控制误差引起的曲轴轮廓误差分别如图8和图9所示。

3.3 基于VMD的曲轴轮廓误差分析结果

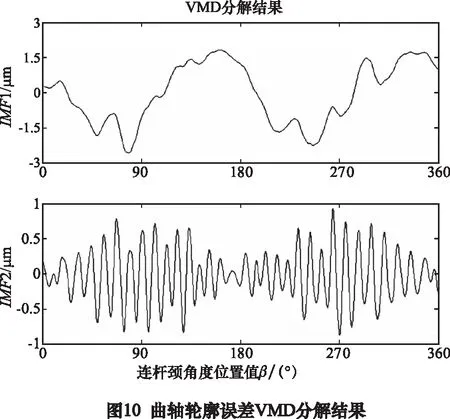
使用VMD进行曲轴轮廓误差分解，必须提前确定分离的IMF数量K。根据第1部分的描述，曲轴轮廓误差主要受到随动磨床C轴和X轴的影响，因此将数量K设置为2，即将原始轮廓误差实验数据分解为2个分量，分解结果如图10所示。

4 讨论

4.1 基于VMD曲轴轮廓误差分析结果讨论

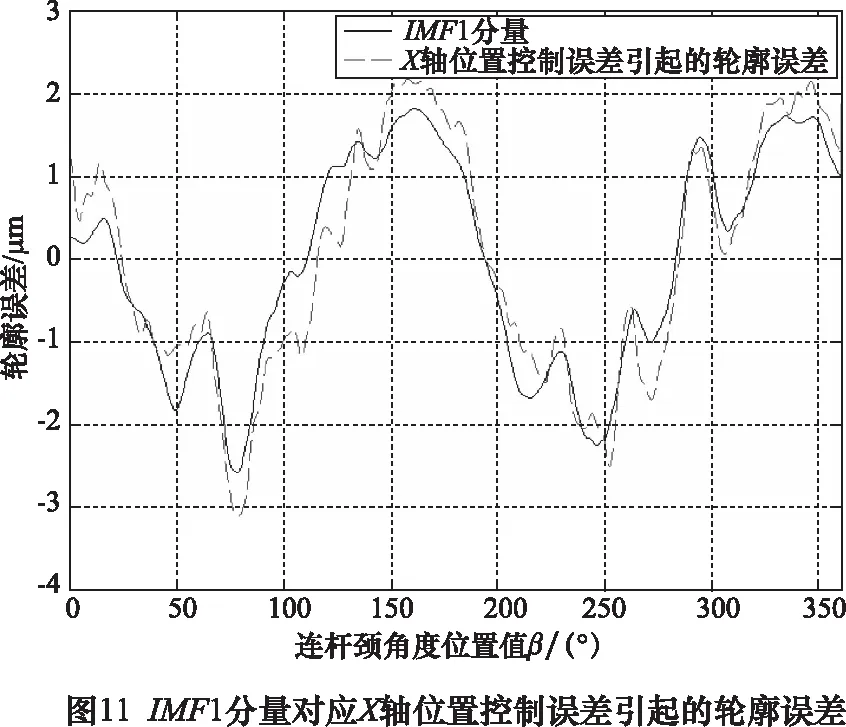
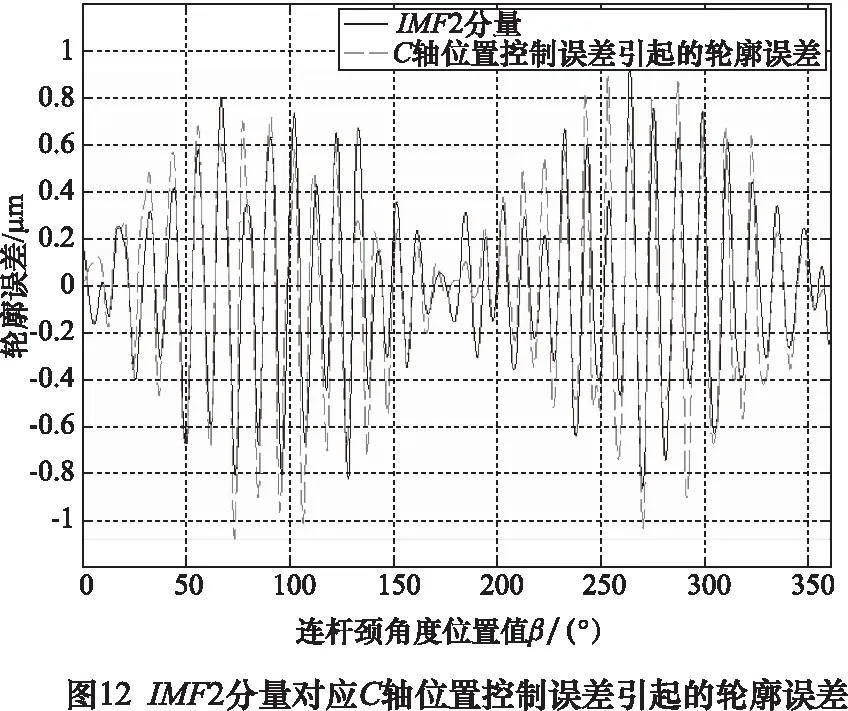
将图10曲轴轮廓误差VMD分析结果分别与图8C轴位置控制误差引起的轮廓误差和图9X轴位置控制误差引起的轮廓误差进行比较，明显可以看出图10中的IMF1分量、IMF2分量分别对应X轴位置控制误差引起的轮廓误差和C轴位置控制误差引起的轮廓误差。该对应关系可由图11和图12进行验证，在图11中IMF1分量基本上与X轴位置控制误差引起的曲轴轮廓误差相同，同样在图12中，IMF2分量基本上与C轴位置控制误差引起的曲轴轮廓误差相同。以上分析和讨论表明，可以通过VMD曲轴轮廓误差分析去预测随动磨床C轴和X轴的性能或性能变化趋势。

4.2 VMD和EEMD轮廓误差分析方法比较

本文提出的基于VMD的轮廓误差分析方法和作者在文献[7]中提出的基于EEMD的轮廓误差分析方法，虽然都能分离出与数控曲轴随动磨床C轴和X轴相对应的分量，从而可以通过这些分离出的分量去分析判断C轴和X轴的性能。两种分析方法相互比较，VMD方法更加方便，更加快速，分解效果也更好。首先，VMD方法没有EEMD方法的边界效应问题和模态混叠问题，EEMD虽然是对EMD方法的改进并用于消除模态混叠，但从实际轮廓误差的分析结果来看，并没有完全消除。其次， EEMD需要在每步EMD之前添加高斯白噪声，因此效率不如VMD。最后，VMD方法可以直接分离出对应C轴和X轴的轮廓误差分量，而EEMD方法不仅在分解前需要对边界做周期拓展，在分解后还需做一些后续的处理和高低频分量的对比分析。

5 结语

本文给出了由数控随动磨床C轴、X轴位置控制误差计算曲轴连杆颈轮廓误差的方法，为找出C轴、X轴位置控制误差与曲轴轮廓误差的对应关系提供了计算依据。

提出了基于VMD的轮廓误差分析方法。通过磨削实验，从数控系统中采集C轴和X轴位置控制误差数据，并测量磨削后的曲轴连杆颈轮廓误差数据。由采集的C轴和X轴位置控制误差数据分别计算其对轮廓误差产生的影响，作为进行轮廓误差分析的对比依据。对测量的曲轴轮廓误差数据进行基于VMD的轮廓误差分析，获得2个IMF分量。

将基于VMD的轮廓误差分析结果与C轴和X轴位置控制误差引起的轮廓误差进行对比分析和验证，得出的结论如下：IMF1分量对应的是X轴位置控制误差引起的轮廓误差，IMF2分量对应的是C轴位置控制误差引起的轮廓误差。将VMD方法和EEMD方法进行对比，基于VMD的轮廓误差分析方法更方便，更快速，分解效果更好。

通过曲轴轮廓误差分析，找出其各分量与数控随动磨床C轴和X轴的对应关系，为从随动磨削工件轮廓误差预测机床关键功能部件性能提供了可能，可以作为关键功能部件预防性维护的依据。对于通过抽检监控方式改进曲轴自动化生产线的效率和加工精度具有重要意义。