基于ABAQUS软件的CFRP筋混凝土梁受力模拟分析**

周逸群

（安徽三联学院机械工程学院，安徽 合肥 230601）

1 概述

在我国当前的建筑行业中，钢筋混凝建筑中质量以及结构设计要求越来越高[1]。钢筋混凝土是建筑工程和行业中最常用和最重要的材料之一。当今建筑工程设计大部分采用钢筋混凝土结构。在我国，钢筋混凝土结构也是使用最广泛的结构形式，占总数的绝大多数，而且中国也是世界上在该地区使用钢筋混凝土结构最多的国家。我国基础建筑设施的建设起步比国外晚，自20世纪80年代起逐渐存在钢筋锈蚀问题[2]。在腐蚀环境中，极易出现因钢筋锈蚀而导致结构或构件损伤严重，降低结构或构件使用年限的同时还带来了昂贵维修费用，不利于可持续发展目标的实现[3-6]。因此，非常有必要研究耐腐蚀的新型材料，以此来解决钢筋锈蚀问题，延长建筑设施使用年限。

建筑材料发展日新月异，国内外有研究者找到一些基本可以克服钢筋锈蚀问题的建筑材料，如纤维增强复合材料（FRP）筋，其具有质量轻、强度高、耐腐蚀性强、绝缘性强等特点[7-9]。纤维增强复合材料主要包括碳纤维增强复合材料（CFRP）、玻璃纤维增强复合材料（GFRP）、芳纶纤维增强复合材料（AFRP）和玄武岩纤维增强复合材料（BFRP）[10]。耐锈蚀是取代钢筋重点考虑的优越性能之一，FRP材料主要是由非金属的纤维材料组合而成，其较小的导电性抑制了材料的电化学过程，对于威胁结构的酸碱腐蚀介质，有良好的抵御性[11-12]。同类材料中，CFRP 耐腐性能高于其他两种。

国内的CFRP筋材料研究项目起步较晚[13-14]，其配筋、型材以及应用于结构的力学性能还有待研究。近年来，国内一些高校和研究院所，如同济大学、东南大学等都对CFRP筋材料及其建筑工程应用进行了深入的研究，并且已经有一些比较完善的成果转化和规范制定。本研究结合以上情况，在ABAQUS平台上，初步建立钢筋混凝土梁结果模型，分别对普通钢筋混凝土梁和带有复合材料CFRP筋混凝土梁进行静态试验，得到基本受力性能模拟值。同时，研究了选用两种不同材料受力的影响，最终模拟结果对于材料的选用和后续的研究具有一定理论指导意义。

2 模型建立及参数设置

2.1 建立几何模型

ABAQUS/CAE是大型有限元分析软件的交互式图形环境，支持三维立体和二维平面的建模空间，也支持可变形部件以及离散刚体、解析刚体等模型类型。可以通过特征化建模，包括将部件通过拉伸、旋转、扫略等方式进行建模，也可通过导入草图、部件、模型或者装配的方式进行建模。本研究采用部件拉伸方式进行建模，类型为指定深度，考虑到实际情况，数值设为2 000。部件的类型为可变形，模型空间为三维，形状为线性，特征类型为平面。

2.2 定义材料属性

在完成建模后，为生成的模型进行定义材料属性。针对CFRP材料的特点，本次模拟主要定义弹性属性，各参数如表1所示。这里不考虑与温度相关的数据。梁桁架截面的面积分别设为113.09和78.53。

表1 弹性属性参数

2.3 定义初始边界条件

在ABAQUS/CAE中，根据需求选择ABAQUS/Standard或者ABAQUS/Explicit进行有限元分析。其中，ABAQUS/Standard作为软件的通用分析模块，应用于各种简单线性及复杂非线性问题的分析场合中，也可进行静力学、动力学、热力学等分析。本研究以ABAQUS/Standard分析模块创建分析步，开始分析过程。得到的分析结果可作为初始条件，采用ABAQUS/Explicit分析模块继续分析，从而解决后续更复杂的工程仿真分析过程研究。将计算过程分成很多增量步，最大增量步默认为100，其值对模型是否收敛影响可以忽略不计。该过程属于自己难以收敛的非线性分析问题，需要不断减小初始增量步，将分析步时间乘以0.01，最小为1E-05，最大为1。后一个增量步利用前一个增量步的计算结果为初始条件继续求解，逐步计算出结果。

由于钢筋是嵌入混凝土的，所以在施加相互作用时采用内置区域来创建约束，权系数舍入误差为1E-006，在分析过程中，绝对外部容差为0，外部百分比容差为0.05。部件初始边界条件如图1所示，部件的初始边界条件。为了提高计算收敛性，荷载加载方式为位移加载，在梁跨中施加沿Z轴负方向的位移，大小为100 mm。

图1 部件初始边界条件

2.4 划分网格

在划分网格之前，首先为每个部分指定网格单元格的类型。网格划分是对几何模型进行的离散化处理，使得在计算机辅助下求解大型非线性偏微分方程组成为可能。网格划分的质量在一定程度上决定仿真分析的精度和时间，网格划分得越粗略，所需要的时间就越短，但是分析精度就会越低；反之，网格划分得越细，计算结果就会越精确，但是使用的计算时间会越长。网格划分单元的形状包括六面体、四面体以及楔形三种。本研究采用六面体单元形状划分网格。六面体单元可以减少部件所划分单元格的数量，提高计算效率。利用六面体单元形状划分网格时，可以采用中性轴（Medial Axis）和进阶（Advancing Front）两种不同算法。本研究中部件网格的划分采用中性轴算法。使用中性轴算法能够得到单元形状比较规则的网格。网格划分图如图2所示。钢筋混凝土梁模型如图3所示，类型为C3D8R（八结点线性六面体单元、减缩积分，沙漏控制）。钢筋骨架模型如图4所示，单元类型为T3D2，即两结点线性三维桁架单元。

图2 网格划分图

图3 钢筋混凝土梁模型

图4 钢筋骨架模型

3 复合材料CFRP钢筋混凝土梁受力过程模拟

CFRP材料Hashin损伤参数如表2所示，其中损伤演化参数如表3所示。损伤稳定性中，纵拉伸方向、纵压缩方向、横拉伸方向和横压缩方向的黏性系数均为0.001。弹性类型为单层板，各参数数据如表4所示，其余参数保持不变。由于替换了带有复合材料CFRP钢筋混凝土梁，因此，建立4层常规壳复合层，以部件全局坐标系中的Z轴作为法线方向，分别旋转0、45°、-45°和90°。在分析过程中进行截面积分。厚度积分规则有Simpson和高斯两种。这里采用Simpson规则。ABAQUS/Explicit作为软件的动力显式分析模块，计算速度较快，稳定性较好。静力通用分析通常使用较多。带有复合材料CFRP钢筋混凝土梁受力过程采用静力通用分析来完成，分析步总时长为1 s。该受力过程属于复杂的非线性问题分析，增量步数应远远大于100，这里最大增量步数为10 000，其他保持不变。由于带有复合材料CFRP筋，因此，约束类型为绑定。施加沿Y轴负方向的位移，大小为50 mm。网格布局有两种类型：边界布局和全局布局。对于规则部分，选择后者。每个组件的全局大小为10，大小控制取决于预期的模型精度和整体大小。这里可以进行很多优化。网格划分通常在需要研究的区域较为精确，在不涉及研究的区域进行粗略划分，以提高计算速度。该单元不同类型为S4R，即四结点曲面薄壳或厚壳，减缩积分，沙漏网络控制，有限膜应变。

表2 CFRP材料Hashin损伤参数

表3 损伤演化参数

表4 弹性数据

4 不同材料受力性能仿真模拟结果与分析

将划分好网格后的模型进行提交作业，可在进行数据分析后，监控运行过程，并且在可视化模块可以直观地看到有限元分析的结果。如图5所示，带有复合材料CFRP钢筋混凝土梁应力场分布，图（a）为受力第1道次，即开始受力应力场分布，图（b）为受力第11道次受力结束应力场分布。由图可知，在外力作用下，外轮廓逐渐变形。在集中力作用处应变值较大，其余部位相对较小。

图5 带有复合材料CFRP钢筋混凝土梁应力场分布图

如图6所示，两种材料应力分析对比图，图（a）为普通钢筋混凝土梁，图（b）为带有复合材料CFRP钢筋混凝土梁。由图可以很直观地看出，采用先进的材料进行优化后，应力分布幅值由优化前的8.411×103变为4.719×103，而且应力幅值的分布也有所变化，说明优化效果明显，即采用带有复合材料CFRP钢筋混凝土梁，可以显著减少变形地方的应力。

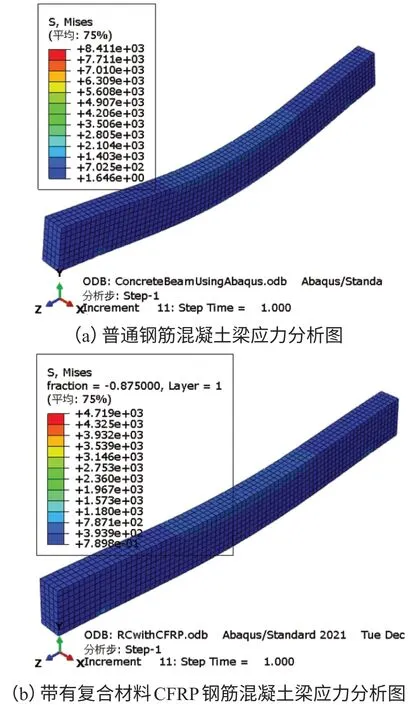
图6 两种材料应力分析对比图

两种材料位移分析对比图如图7所示，图（a）为普通钢筋混凝土梁，图（b）为带有复合材料CFRP筋混凝土梁。从图可知，普通钢筋混凝土梁位移分布幅值为1.172×102，带有复合材料CFRP筋混凝土梁位移分布幅值为5.855。因此，从结果看出，梁的受力过程基本符合理论计算和试验研究，误差在允许的范围之内，体现了新型材料的优势和特性。本研究采用的建模方式具有一定可靠性，受力性能仿真模拟过程为后续相关更深入的研究提供一定的参照和基础。在实际工程的应用中可以通过建立正确的模型，先对结构进行受力分析。

图7 两种材料位移分析对比图

5 结语

本研究对普通钢筋混凝土梁和带有复合材料CFRP筋混凝土梁的受力性能开展初步研究，利用ABAQUS对受力过程进行建模仿真模拟，得到带有复合材料CFRP筋混凝土梁的优化效果，通过对这些结果的分析可以为后续的工艺设计等提供可靠的仿真依据。如CFRP筋混凝土梁的挠度研究，尤其是长期挠度的研究分析。CFRP筋虽然能够有效地克服普通钢筋的锈蚀问题，但也存在一系列缺点。如弹性模量较低，会导致构件刚度不足，裂缝过大。因此，还要对CFRP筋混凝土梁裂缝宽度展开具体的计算。在实际的工程应用中，如何以经济效益为主，合理地配置钢筋，是今后努力的方向。