大气层内固体火箭实时轨迹优化方法

郝泽明,张 冉,王嘉炜,李惠峰

(北京航空航天大学宇航学院,北京 100083)

0 引 言

固体火箭能量管理是指通过调整固体火箭的飞行程序角,使固体火箭对剩余燃料进行消耗,并在燃料耗尽关机时满足指定的终端状态。文献[1]早期提出了一种能量管理方案,通过在主动段进行姿态调制消耗多余的能量。但该方法适用的飞行时间短,且需要离线设计,难以控制终端速度大小。文献[2]提出了交变姿态控制能量管理方法(Alternate attitude control energy management,AEM),文献[3]提出了一般能量管理方法(General energy management,GEM)。文献[4]在传统能量管理方法基础上,提出了一种闭环动态逆能量管理方法,得到更有利于姿控系统执行的控制指令。这几种方法均在真空段对固体火箭进行能量管理,且难以严格满足终端高度、速度与倾角的约束。文献[5]提出了一种多约束制导方法,其可以对固体火箭速度进行管控,但仍只能在真空段进行管理。文献[6]提出了样条能量管理方法(Spline energy management,SEM),该方法综合了AEM与GEM方法,能够处理一些大气层内过程约束。文献[7]对传统能量管理方法进行了改进,提出了一种新的视速度模量计算方法,能够适应低弹道多约束的能量管理问题。

大气层内固体火箭需要在满足过程约束情况下机动飞行以达到指定的终端状态,因此如何严格满足过程约束与终端约束是大气层内能量管理问题的关键。上述方法多数在真空段进行能量管理,仅有少数方法可用于大气层内的能量管理,且难以严格满足全部约束。同传统能量管理方法相比,轨迹优化方法可以严格满足过程与终端约束,但能量管理问题只需得到一条可行轨迹,不存在明确的性能指标。因此本文构造了性能指标,将能量管理问题转化为轨迹优化问题,并采用轨迹优化方法进行在线求解,既对固体火箭进行了能量管理,同时也满足了各项约束。针对轨迹优化问题的求解,常见的方法主要是将问题建模为最优控制问题进行求解,包括两点边值求解算法[8-9]、非线性规划求解算法[10-13]、凸规划[14-15]等方法。大气层内固体火箭能量管理问题需要有较高的实时性,而凸规划方法有不依赖初始猜想、收敛性稳定、求解速度快等特点[16],尤其是对于特定形式的凸规划问题,如线性规划、二阶锥规划和半正定规划问题,其求解算法成熟可靠并已具备在嵌入式系统上运行的能力。上述特点使凸规划方法能够满足航天任务中对轨迹优化算法在可靠性、实时性与适应嵌入式系统等方面的要求。然而,在解决实际问题的过程中,并非所有的问题都能够直接建模成凸形式,往往需要对原问题模型进行凸化处理。在基于凸规划的火星着陆轨迹优化中[17],提出了无损凸化方法,其利用变量代换与凸松弛技术对非凸动力学进行凸化,并应用极大值原理证明了凸规划问题与原问题解的等价性,该无损凸化方法已广泛应用于多种场景的轨迹优化问题中[18-19]。

对于大气层内上升段问题,固体火箭飞行受气动力影响,且飞行过程中存在攻角、动压、过载等过程约束,使原轨迹规划问题具有较强的非线性。气动力与火箭推力不同,其通常与攻角、马赫数等直接有关,而这两者又与状态量和控制量直接耦合,因而尚无成熟完备的无损凸化技术可以处理强非线性动力学与过程约束。针对这种情况,通常在给定参考轨迹的情况下对非线性动力学与约束进行线性化处理,并根据求解结果更新参考轨迹进行迭代求解,这种方法被称为序列凸规划方法[20-22]。对于固体火箭,其推力与秒耗量通常为时间的函数,即飞行过程中任意时刻的推力幅值与质量均为已知。由于这种推力不可调的特性,在气动力与过程约束存在的情况下,传统的无损凸松弛技术[17]难以满足,可能会导致问题的求解结果不满足真实动力学。

本文的主要创新点在于采用轨迹优化的思路求解固体火箭能量管理问题,其能够系统的处理约束并增强算法的适应性。在将能量管理问题转化为轨迹优化问题时,通过规则化方法主动构造了性能指标,并采用邻近-牛顿-康托维奇凸规划、控制平滑以及虚拟控制等技术,改善了算法性能：首先,在性能指标中引入推力方向的邻近规则化项,显著提高了算法的收敛性；然后,在优化问题中加入了推力方向变化角速率约束与控制平滑指标,并在离散系统中通过数值微分表示推力方向的变化,同传统方法相比,该方法避免出现奇异弧并提高了求解速度；最后,在推力方向幅值约束与动压约束中引入虚拟控制变量并在性能指标中对其进行惩罚,保证了凸规划子问题在迭代过程中的可行性,降低算法对初始猜想的依赖。仿真实例表明,采用所提出的轨迹优化方法求解能量管理问题是有效的,能够严格满足各项约束并实现高精度终端；此外,算法在地面平台具有百毫秒级的运算速度,具有优异的实时性,能够满足能量管理对求解速度的要求。

1 大气层内固体火箭能量管理问题描述

本文研究固体火箭上升段在纵向平面内的质心运动,假设发动机推力始终沿体轴方向,发动机推力幅值和秒耗量全程已知,忽略地球自转并采用球形重力场。定义平面大地坐标系OXYZ：以发射点为原点O,X轴指向火箭发射方向,Y轴沿铅锤方向指向天空,Z轴由右手定则确定。固体火箭在平面大地坐标系下无量纲化(下文中的变量均为无量纲化的)运动学方程为：

(1)

式中：r∈3表示位置；V∈3表示速度；T表示发动机推力幅值;m表示固体火箭质量,其均为时间的函数且已知；1T∈3表示发动机推力方向并满足3为纵向平面内与1T垂直的单位矢量；A与N分别表示轴向气动力大小与法向气动力大小；g∈3表示火箭所受重力加速度；轴向气动力大小与法向气动力大小的表达式如下：

(2)

式中：ρ(r)表示r处的大气密度；Sref表示参考面积；V表示速度模值;Cx与Cy分别为轴向力系数与法向力系数,其均为马赫数Ma与攻角α的二元函数。以位置与速度作为状态量,定义：

(3)

以推力方向作为控制量,将运动学方程写为紧凑形式：

(4)

固体火箭上升段在飞行过程中应严格满足过程约束,包括攻角约束、动压约束以及法向过载约束,其表示方法如下：

|α|≤αmax

(5)

(6)

(7)

式中：αmax表示允许的最大攻角；qmax表示允许的最大动压；nmax表示允许的最大法向过载。值得注意的是,由于攻角可以表示为推力方向与速度的函数：cosα=VT1T/V,因此攻角范围约束可以表示为：

VT1T≥Vcosαmax

(8)

本文考虑的终端约束包括终端高度范围约束、终端两轴速度范围约束,其可以表示如下：

(9)

综上所述,本节定义了大气层内上升段固体火箭能量管理问题。解决此类问题一般采用开环姿态调制或闭环能量管理的方法,此类方法通常难以处理过程约束,因而一般选择在真空段进行能量管理。轨迹优化方法能够满足严格的过程约束与终端约束,其可以用于解决大气层内上升段问题。因此,本文在下一节中将固体火箭能量管理问题转化为轨迹优化问题进行求解。

2 大气层内固体火箭能量管理轨迹优化问题建模

针对传统能量管理方法难以严格满足大气层内过程约束的不足,本节提出一种对控制量模值积分进行惩罚的规则化方法,该方法主动构造了一个性能指标,将大气层内固体火箭上升段能量管理问题转化为了轨迹优化问题。

(10)

并通过规则化[23-24]方法构造性能指标：

(11)

式中：t0为飞行初始时刻；tf为飞行终端时刻；γ1>0为惩罚因子。因此,大气层内固体火箭上升段轨迹优化问题为：

问题1:大气层内固体火箭上升段轨迹优化问题

(12)

式中：t0为飞行初始时刻；tf为飞行终端时刻；fa(α,Ma)为气动合力,其只与攻角α和马赫数Ma相关；r0为初始位置；V0为初始速度。

该规则化方法对控制量的等式约束进行了松弛,将非凸控制约束转化为了凸约束,易于轨迹优化问题的求解。同时,当惩罚因子γ1足够大时,可以证明这种松弛方式是无损的。

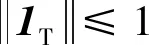
证.大气层内固体火箭上升段轨迹优化问题是一个最优控制问题,其Hamiltonian函数为：

(13)

根据极大值原理,有:

(14)

不妨设协态变量λV与控制量1T的夹角为Θ1,与气动合力fa的夹角为Θ2,则其示意图如图1所示。

图1 控制变量与协态变量示意图Fig.1 Illustration of control variables and costate variables

则问题1的Hamiltonian函数可以表示为：

(15)

当惩罚因子γ1足够大时,有:

(16)

3 邻近-牛顿-康托维奇凸规划方法

根据Newton-Kantorovich迭代方法[25],对问题1的运动学方程进行广义泰勒展开,得到：

(17)

考虑推力方向变化角速率约束,其可以在后续离散化过程中直接处理；而对于攻角约束,由于迭代过程中固体火箭的状态量变化相对剧烈,而控制量变化相对平缓,因此为保证问题的收敛性,仅对控制量进行广义泰勒展开。定义x(i)为当前迭代对应的广义泰勒展开点,则攻角约束为：

(18)

考虑除上述约束外的过程约束,将其表示为紧凑形式：

ψp(t,x,1T)≤0

(19)

终端不等式约束的紧凑形式为：

ψf(tf,xf)≤0

(20)

将上述约束进行广义泰勒展开,得到：

(21)

对性能指标进行广义泰勒展开,得到：

(22)

在性能指标中加入邻近项,形成邻近-牛顿-康托维奇子问题：

问题2：邻近-牛顿-康托维奇子问题

(23)

式中：γ2>0为邻近项对应的惩罚因子。

邻近-牛顿-康托维奇凸规划方法的广义泰勒展开点更新方式如下：

x(i+1)=x(i)+δx

(24)

(25)

若邻近-牛顿-康托维奇子问题的迭代求解收敛,则其可收敛至原轨迹优化问题的局部最优解。将大气层内固体火箭上升段轨迹优化的最优控制问题转化为邻近-牛顿-康托维奇子问题迭代求解,可以将强非线性的运动学方程与约束条件转化为线性形式,便于采用凸规划方法实时求解。

4 实时轨迹优化算法实现

本节介绍邻近-牛顿-康托维奇凸规划的具体实现方法。首先,采用等时间间隔离散方法：

(26)

运动学方程的离散采用一阶保持器,其假设控制量在相邻两离散点间是线性变化的,即:

(27)

因此,离散后的动力学方程为：

(28)

其中,状态转移矩阵Φ(tk+1,tk)满足：

(29)

(30)

式中：

(31)

针对过程约束,其离散形式为：

(32)

针对性能指标,采用欧拉法进行数值积分得到离散化的性能指标：

(33)

在实际工程应用中,轨迹优化所得结果应易于被姿态控制系统跟踪,因此考虑加入推力方向变化角速率约束,使得优化所得推力方向不会出现较大的跳变。针对该约束,通常在连续系统中以推力方向的导数(或变化角速度)为控制量,以推力方向为状态量建立最优控制问题。然而这种处理方式增加了问题的维度,并且引入了额外的状态约束,使问题的求解变得更加困难。本文的处理方式是在离散系统中以数值微分对推力方向进行约束,在引入规则化方法的情况下,其可以避免奇异弧且具有更快的求解速度,类似的处理方式也出现在文献[26] 中。离散系统中的推力方向几何示意图如下：

图2 推力方向几何示意图Fig.2 Geometry schematic of thrust direction

根据图中几何关系,有：

(34)

式中：ωφ为推力方向变化角速率。因此,推力加速度变化加速度约束可以表示为：

(35)

其为二阶锥约束,可以采用凸优化方法直接求解。

此外,为使优化所得推力方向变化尽可能平滑,设计如下性能指标：

(36)

因此,离散化后的子问题为：

问题3:离散Proximal-Newton-Kantorovich子问题

(38)

根据邻近-牛顿-康托维奇凸规划迭代求解方法,需要给定初始轨迹以开始迭代。而由于原问题具有较为严苛的过程约束,因而任意给定的初始轨迹易使问题出现不可行,从而导致迭代终止。因此,在控制约束和过程约束中引入虚拟控制变量κ1、κ2：

(39)

并在性能指标中加入相应的惩罚项：

maxJ2=-γ4κ1-γ5κ2

(40)

式中：γ4,5为正实数。二阶锥规划问题为：

问题4:二阶锥规划问题

maxJ=J1+J2

(41)

从数学角度考虑,引入的虚拟控制变量实际上是一种精确罚函数,其具有如下性质：

性质1.若原问题存在可行解,且γ4与γ5足够大时,虚拟控制变量κ1与κ2的收敛解为零,引入的虚拟控制变量对原问题的求解结果无影响。该性质的证明如下。

(42)

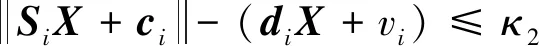
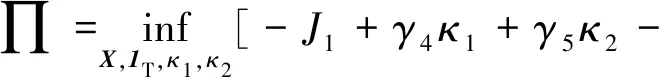
(43)

式中：

(44)

为使Lagrange对偶函数有界,需要满足：

(45)

因此,当γ4与γ5满足：

(46)

则虚拟控制变量κ1与κ2的为零。

文中描述的二阶锥规划问题,其可以采用ECOS软件[27]求解。针对上述算法设计迭代终止条件为：控制量增量与虚拟控制变量小于容许误差,即

σ2≤ε1,κ1,2≤ε2

(47)

式中：ε1为控制量增量容许误差；ε2为虚拟控制变量容许误差。

5 仿真校验

本节采用大气层内固体火箭上升段轨迹优化问题的具体实例对所提出的基于邻近-牛顿-康托维奇凸规划的轨迹优化方法进行仿真校验。本文所采用的仿真数据为：地球半径为6371004 m,地球引力常数为3.986005×1014m3/s2,大气密度模型和声速模型拟合自美国标准大气1976；固体火箭的初始质量为5400 kg,发动机推力为130 kN,秒耗量为50 kg/s,参考面积为0.5 m2,飞行时间为75 s,轴向力系数和法向力系数为：

(48)

式中：

(49)

固体火箭初始时刻以10 m/s的速度垂直起飞；在飞行过程中,要求飞行攻角绝对值全程不大于10°,终端攻角绝对值不大于1°；飞行过程中的动压不超过70 kPa,法向过载不超过4。在用凸规划求解该问题时,取离散点数量N为40,控制量增量容许误差ε1取1×10-1；虚拟控制变量容许误差ε2取1×10-4。仿真选择如表1所示的三种工况,其分别表示能量管理能达到的最小、中间及最大终端速度,这三种工况的仿真结果如下。

表1 仿真工况Table 1 Chemical composition of experimental alloy

图3给出了固体火箭三种工况下的纵向平面内的位置与速度曲线。从图中可知,固体火箭能够严格满足终端高度约束与终端两轴速度约束。图4分别给出了固体火箭飞行过程中的俯仰角与攻角曲线。从图中可知,固体火箭在工况一情况下需要达到较小的终端速度,因而轨迹优化方法优化得到了摆动形式的姿态角。轨迹优化所得结果与传统能量管理方法的姿态调制结果相似,但能够严格满足终端约束,并且无需人为设计调制方式,在大气层内上升段其终端速度具有约10%的调节能力。

图3 纵向平面内位置与速度轨迹Fig.3 Position and velocity trajectories in longitudinal plane

图4 俯仰角与攻角曲线Fig.4 Pitch angel and angel-of-attack

图5表示三种工况下的过载与动压曲线。从图中可知,固体火箭飞行全程均满足过载与动压约束,表示轨迹优化方法所得轨迹满足过程约束。同时,为了验证轨迹优化方法的优化精度,根据三种工况下轨迹优化所得俯仰角曲线,对其进行开环数值积分,得到如表2所示的优化误差。从表中可知,轨迹优化方法所得的终端高度与速度均具有米级精度,表示轨迹优化方法所得结果满足动力学约束。

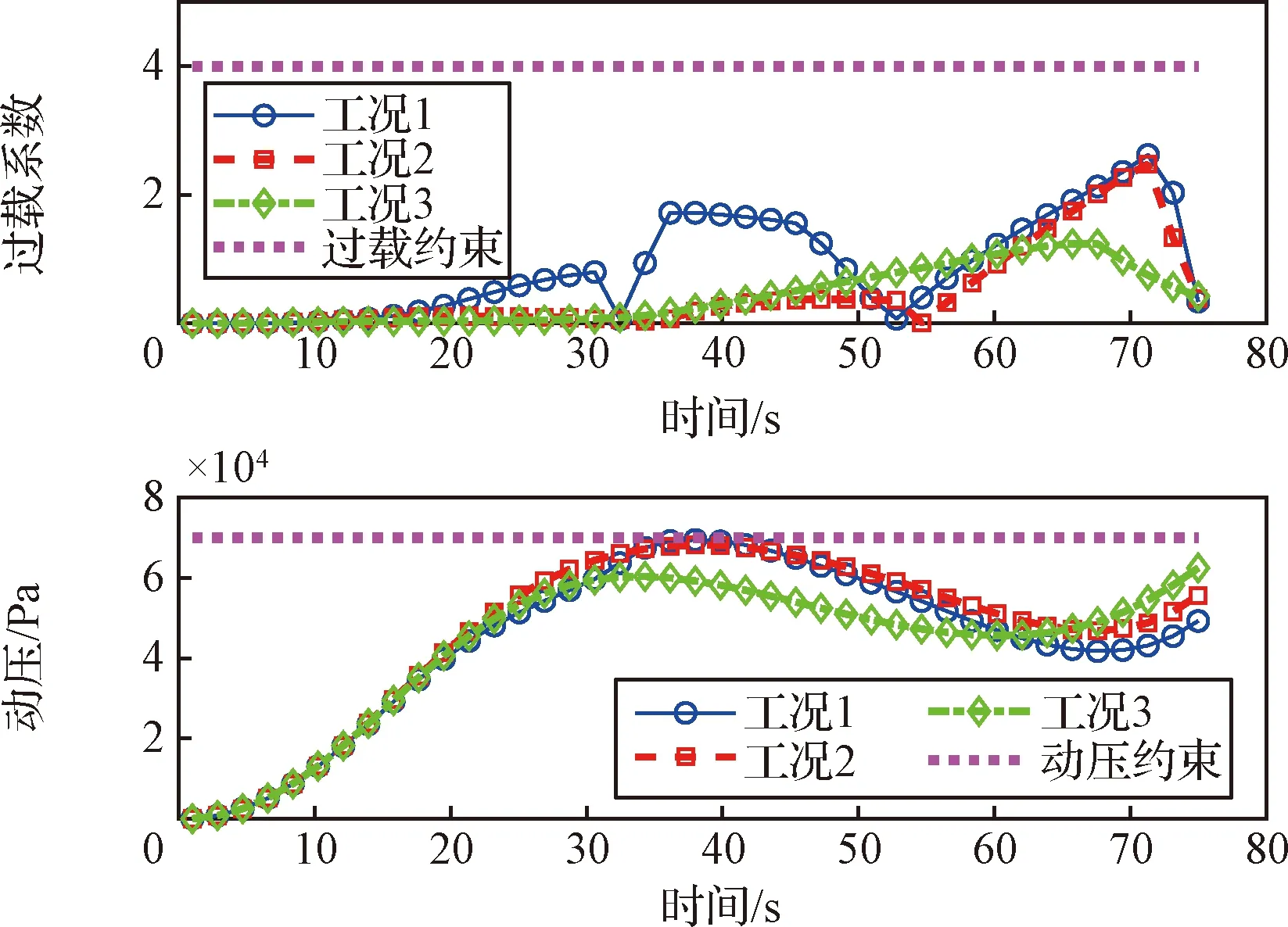
图5 过载与动压曲线过载系数Fig.5 Overload and dynamic pressure

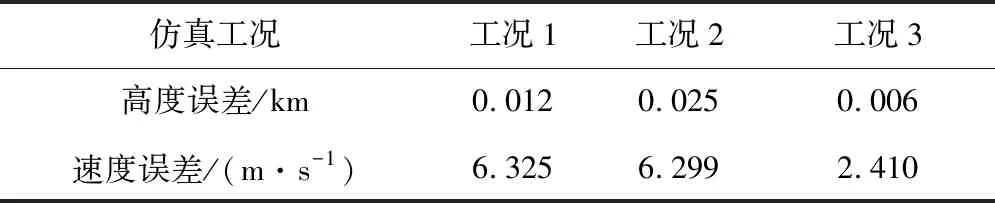
表2 轨迹优化误差Table 2 Trajectory optimization errors

为进一步验证本文所提出轨迹优化方法的正确性与有效性,以工况1为例进行仿真与对比。图6所示为攻角与动压对比结果。首先考虑本文提出的控制平滑方法,从图中可知,加入了控制平滑指标的飞行攻角相比未加入的更为平滑,这是由于控制平滑指标是在离散系统中对推力方向二阶差分模值积分进行了惩罚,这种处理方式在连续系统中相当于最小化推力方向二阶导数的变化率。因此在这种处理方式下,推力方向的变化更为平缓,这在飞行攻角曲线上的体现为：加入了控制平滑指标的攻角曲线其拐点较少,而不加入该指标的攻角曲线拐点较多,且加入了控制平滑指标的曲线拐点两侧攻角变化角速度突变更小。从数学角度考虑,光滑函数要求函数无穷阶连续可微,而离散系统中的拐点表示该点连续但不可微,因此可以认为拐点较少的攻角曲线其光滑程度更好。从实际工程角度考虑,拐点前后的攻角角速度若具有较大的突变,姿态控制系统在跟踪该指令时,其跟踪效果会受到较大影响。若轨迹优化所得攻角曲线具有较多拐点且拐点前后攻角角速度具有较大突变,则该轨迹在实际工程中不利于姿态控制系统跟踪。因此,本文考虑的控制平滑指标可以提高轨迹优化所得控制量的光滑程度,使其在实际应用中更易于被姿态控制系统跟踪。

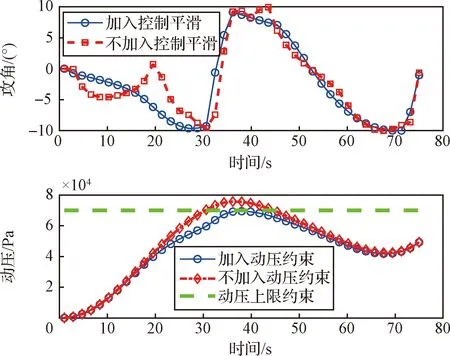
图6 攻角与动压对比Fig.6 Comparison of angle-of-attack and dynamic pressure

考虑固体火箭上升段需要满足的过程约束。以动压约束为例,从图6中可知,在不加入动压约束情况下,飞行过程中的最大动压约为75 kPa,高于任务要求的70 kPa。在加入动压约束情况下,固体火箭全程动压均不超过动压上限约束,表明动压约束产生实际作用,本文提出的轨迹优化方法能够严格满足过程约束。

图7给出了轨迹、攻角与虚拟控制变量的部分迭代过程。从图中可知,初始轨迹与最终收敛轨迹的差异较大,但本文所提出的轨迹优化方法能够在初始轨迹偏差较大的情况下使轨迹收敛。值得注意的是,第一次迭代中的虚拟控制变量均不为零,表示初始轨迹偏差较大,若不加入虚拟控制变量则问题无可行解,导致迭代无法进行。

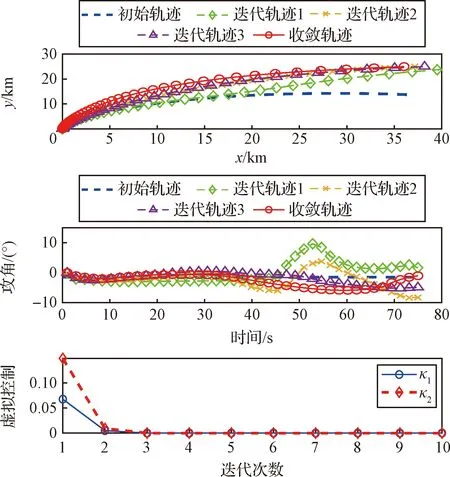
图7 轨迹、攻角与虚拟控制变量的迭代过程Fig.7 Trajectory,angle-of-attack and virtual control variables in iterations

传统能量管理方法多数为制导方法,通常其难以直接处理过程约束,且多数在固体火箭三级进行能量管理。本文采用轨迹优化则与之不同,其能够直接对过程约束进行处理,并能够在固体火箭一级进行能量管理。因此为验证所提出轨迹优化方法的性能,以工况1为例,采用伪谱法求解能量管理问题得到可行轨迹,与本文的轨迹优化结果进行对比。

本文以纵向平面内的为位置、速度、俯仰角以及俯仰角速率作为状态量,以俯仰角角加速度作为控制量,分别以最小化俯仰角角加速度模值积分为性能指标,采用GPOPS软件[28]求解轨迹优化问题,其仿真对比结果如图8所示。

从仿真结果可以看出,采用伪谱法能够求解本文所提出的轨迹优化问题,实现了对固体火箭的能量管理,同时满足了动压、过载等过程约束。这表明本文通过构造性能指标将能量管理问题转化为轨迹优化问题的方法是正确可行的。从仿真对比结果可以看出,伪谱法优化所得结果与本文优化结果存在差异,这是由于能量管理问题存在多个局部最优解,两种不同的非线性规划方法可以得到不同的可行解。最终,在i7-8565 CPU 1.8 GHz环境下,利用GPOPS软件求解能量管理问题,其离散点数量为329,求解时间为6.79 s；与此相比,在同一环境下运行本文所提出的轨迹优化算法,其平均计算耗时为83 ms。因此,本文所提出方法在对固体火箭进行能量管理的同时,具有良好的收敛性与更快的计算速度。

6 结 论

本文提出一种邻近规则化技术,将固体火箭能量管理问题转化为轨迹优化问题,并提出一种邻近-牛顿-康托维奇凸规划的轨迹优化方法,实时求解了大气层内固体火箭上升段轨迹优化问题。结论包括：

本文提出的规则化技术将固体火箭能量管理问题转化为轨迹优化问题,并应用最优控制理论对其进行了理论分析,证明轨迹优化问题的解是能量管理问题的可行解；本文提出一种邻近-牛顿-康托维奇凸规划方法,避免算法求解出现奇异弧、提高了求解速度并保证了凸规划子问题在迭代过程中的可行性。数值仿真结果表明,采用该方法求解轨迹优化问题能够满足动力学与各项约束,优化所得控制量易于被姿态控制系统跟踪,算法具有良好的收敛特性与实时性且对初始猜想不敏感。