变电站巡检定位跟踪的智能化应用研究
2022-01-17陈再胜王颜霞
杨 娜,陈再胜,王颜霞
(1.商丘工学院信息与电子工程学院,河南 商丘 476000;2.西京学院机械工程学院,陕西 西安 710199)
0 引言
随着现代化进程的加快,广大人民群众的日常生产生活对电力的需求愈加旺盛,因此智能变电站相关技术得到不断的发展[1]。为了保障电力的正常、稳定供应,智能变电站需要优化其运行维护工作的相关技术,因此智能变电站定位跟踪技术的重要性愈加凸显[2]。由于传统的人工巡检具有一定的滞后性和欠稳定性,采用巡检机器人进行相关的定位跟踪任务势在必行[3]。基于卡尔曼滤波跟踪算法的相关技术具有较强的可操作性。该技术可帮助巡检机器人对障碍物进行识别并躲避,准确地定位巡检目标点,规划巡检的工作路径,高效、智能地完成巡检任务[4]。鉴于此,本文将以卡尔曼滤波跟踪算法等相关技术作为研究重点,挖掘更优质的智能变电站定位跟踪技术。
1 卡尔曼滤波跟踪算法
卡尔曼滤波跟踪算法的本质是一种线性系统状态方式,通过系统输入观测数据,对存在噪声的输入与观测信号进行处理,进而对系统的状态进行最优估计,即滤波[5]。卡尔曼滤波跟踪过程可表述为两种形式:其一为根据已知运动状态方程,在线性空间中对目标随后的状态进行预测;其二为分布确定且均值为零的随机过程。卡尔曼滤波的基本方程中,设在(k+1)时刻,其估计状态可表述为x(k+1)。同理可知,k时刻的状态表示为x(k)。状态方程为:
x(k+1)=F(k+1,k)x(k)+V(k)
(1)
式中:V(k)为系统噪声序列;F(k+1,k)为k时刻的一步转移矩阵。
基于此,卡尔曼滤波的观测矩阵如式(2)所示。
Z(k)=C(k)x(k)+W(k)
(2)
式中:C(k)为观测矩阵;W(k)为跟踪过程中存在的观测噪声序列。
V(k)与W(k)在一般情况下满足式(3)~式(5)。
(3)
式中:Q(k)为系统中的噪声方差矩阵。
(4)
式中:R(k)为观测噪声方差矩阵。
E[V(k)W(j)T]=0
(5)
卡尔曼滤波的初始条件包含一步预测的状态向量估计、一步预测状态误差的相关矩阵、输入的观测向量序列等。为了更加透彻地理解卡尔曼滤波原理,可以举例进行详细阐述:假设一辆汽车在马路上正常行驶,则该辆汽车的状态可用其实时位置与行驶速度来表示,如式(6)所示。
xt=[ptvt]T
(6)
式中:pt为该辆汽车在t时刻下的位置;vt为t时刻的行驶速度。
汽车的速度不是一成不变的,具有一定的可控性与可变性。驾驶员可通过踩油门、换挡、踩刹车等方式对汽车的速度进行控制。设控制量为ut,则有:
(7)
vt=vt-1+ut×Δt
(8)
由于式(7)与式(8)中的输出变量均为相关输出变量的线性组合,表明了输入状态与输出状态中存在线性组合关系,因此可将其表示为以下矩阵形式。
(9)
式(9)可简化为如式(10)所示的卡尔曼滤波中的状态预测公式。
(10)

(11)
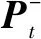
2 基于卡尔曼滤波的匹配定位跟踪技术
2.1 智能变电站定位技术分析
在智能变电站中可以运用巡检机器人来保障电力设备的稳定运行。该过程中需要用到全球定位系统(global positioning system,GPS)/航位推算(dead reckoning,DR)组合导航定位技术。该技术具有较强的高效性与实时性,可以即时、准确地实现对巡检机器人的定位[6]。其中,GPS导航的原理是一种基于卫星的距离修正。当用户需要定位时,通过GPS将卫星的位置作为已知的参考位置点,随后测量用户与参考卫星之间的距离,进而推算出用户自身的准确位置。然而不可避免的是,在定位过程中,接收器有一定的概率会产生定位精度上的误差,甚至在计算距离时可能会出现延迟误差等干扰情况,最终导致定位结果不够准确。另一方面,DR指的是一种基于二维空间的导航定位技术,其本质为通过数字分析与推算来锁定目标巡检机器人的位置。
航位推算原理如图1所示。

图1 航位推算原理图Fig.1 Schematic diagram of DR
图1中表示的是DR将陀螺仪与里程计结合在一起,对巡检机器人的角度值、路径、路程进行测量与规划。图1中:横坐标轴表示的是地理方位中的东方;纵坐标轴则表示朝向为北方。在系统运行开始时,巡检机器人在这两个方位坐标下的初始位置的相关信息及数据是已知的,根据陀螺仪与里程计实时测量出其位姿信息,即其航向角θn与里程Sk。在k时刻,巡检机器人的位置信息与航向信息的计算式分别如式(12)与式(13)所示。
(12)
(13)
DR技术的优势在于其定位精度具有一定的稳定性,不会受到其他干扰因素的影响。但不可避免的是,该技术也存在一些弊端。当获取位姿信息时,传感器存在累积误差,且该误差会随着时间的延长而持续累积。因此,该技术仅适用于短时间内的导航定位,具有短时性。鉴于此,此次研究将GPS与DR两种定位技术进行有机的结合,并将其应用到智能变电站的巡检机器人定位中,使其自身所处的位置信息与时刻累积后的位置变化信息都能够被获取,且精度较高。在综合运用GPS/DR技术时,为了融合二者输出的导航数据、有效地排除累积误差及其他干扰因素的影响,采用卡尔曼滤波器对数据进行融合处理。GPS/DR系统的数据融合如图2所示。
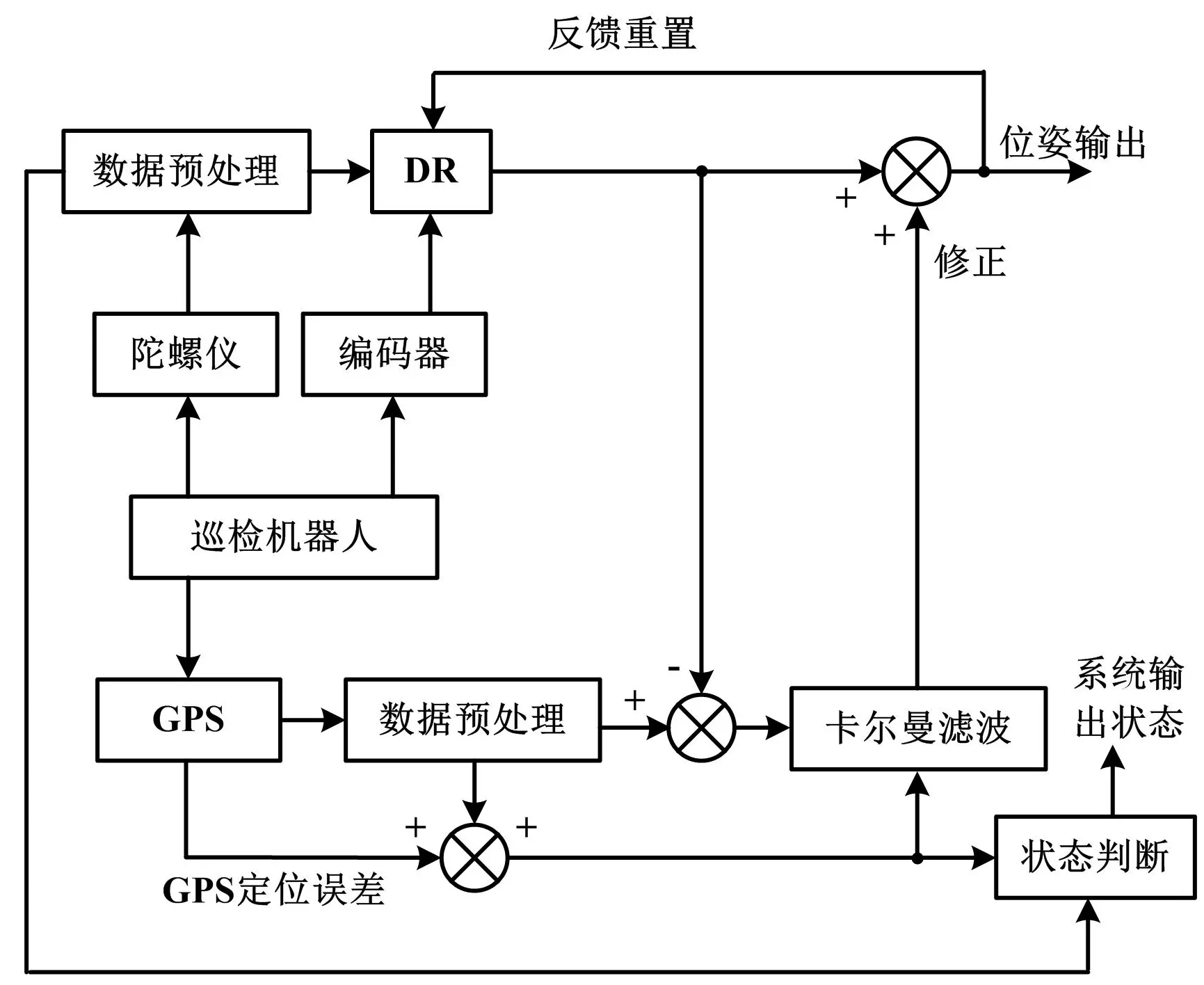
图2 GPS/DR系统的数据融合Fig.2 Data fusion of GPS/DR system
由图2可知,智能变电站中的巡检机器人利用GPS/DR导航技术。通过卡尔曼滤波器对智能导航系统的输出状态进行估计。在此基础上,采用该估计值对导航的数据进行持续不断的修正,进而完成两个导航系统输出数据的有机融合。此外,还需从运动学的角度入手,对智能变电站中巡检机器人的运动模式进行分析。智能变电站巡检机器人的运动模型如图3所示。
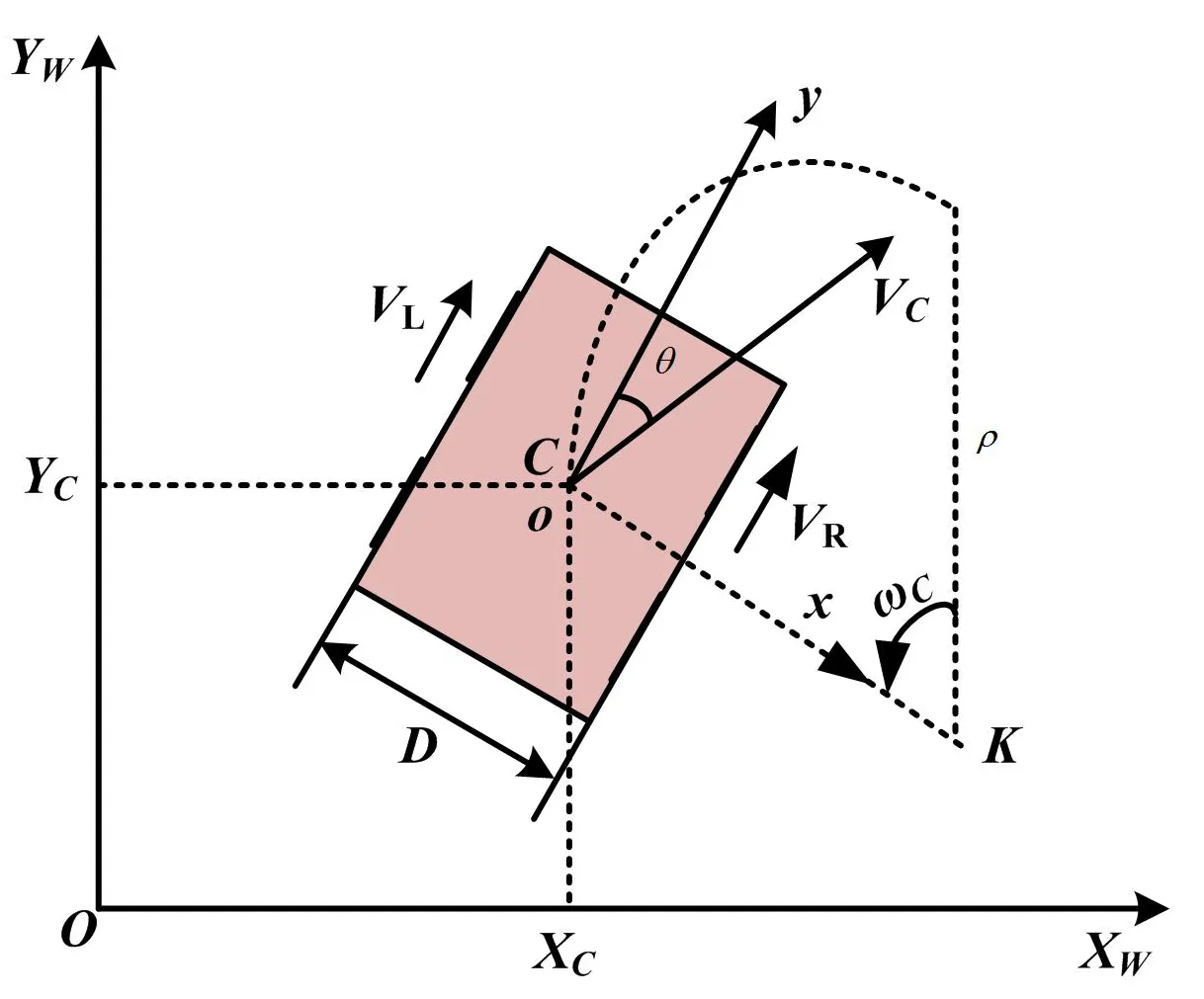
图3 智能变电站巡检机器人运动模型Fig.3 Motion model of intelligent substation inspection robot
由图3可知,巡检机器人的运动控制主要是通过左右两轮之间速度的差值来完成的。巡检机器人在运动过程中,其车轮与地面不可避免地产生摩擦,且不同的车轮有着不同的行驶速度,因此会导致巡检机器人出现侧滑,进而使定位的结果出现一定的偏差。基于此,可以令图3中巡检机器人的质心C在平面坐标系XWOYW中的投影坐标为(XC,YC),θ为坐标系xoy中机器人运动方向与纵坐标的夹角(即姿态角)。则机器人的运动学方程为:
(14)
式中:D为该巡检机器人的车身宽度;ωC为C的角速度;VC为线速度。
机器人左右车轮的速度不同,分别用VL、VR表示,再将其与角速度和线速度的计算式相结合。则巡检机器人的运动学方程为:
(15)
通过式(15)可知,要避免侧滑甚至定位误差、改变机器人的位姿或者其行驶的方向,只需改变该机器人的VL、VR即可。
图3中,ρ为机器人的曲率半径,其计算式为:
(16)
式(16)表明:机器人是作直线运动还是作旋转运动,由VL和VR的取值决定。
2.2 基于扩展卡尔曼滤波的跟踪
当卡尔曼滤波在非线性系统中进行应用时,需要将非线性系统近似线性化处理,再采用卡尔曼滤波对系统的状态进行最优估计。该方法被称为扩展卡尔曼滤波法[7]。在估计过程中,首先需要构建离散模型,如式(17)所示。
(17)
式中:f为非线性方程;W为系统运行过程中的噪声。
P为该系统的协方差矩阵,需要利用式(18)对其进行更新。
(18)
式中:F为系统的矩阵形式;Q与式(11)中的含义相同,代表着测量噪声。
对卡尔曼增益进行计算,算式为:
(19)
在计算出卡尔曼增益后,可以结合该项数据对当前状态的最优估计值进行计算,则有:
(20)
在此基础上,可以得到扩展卡尔曼滤波后对系统的相关测量值与估计值。将其与真实值进行对比分析,即可计算出误差,进而判断出扩展卡尔曼滤波的准确性[8]。巡检机器人的系统方程为:
(21)

令观测量为z=[rα]T,δr、δα为白噪声的误差,则观测方程为:
(22)
随后计算系统矩阵F、测量矩阵H。
(23)
(24)
将式(22)~式(24)代入式(17)~式(21)中,得到障碍物运动的实际值等,进而达到巡检机器人预估的效果。
3 试验与分析
根据对卡尔曼算法及基于卡尔曼滤波的匹配定位跟踪技术的研究,本文针对巡检机器人的运动控制,设计了模糊推理控制系统。该系统的控制规则为:对被控对象或过程进行模糊推理。其输出量为K,即斥力增压[9-10]。由于推理所得结果是一个较为模糊的量,被控对象(即巡检机器人)不能将其直接应用到巡检工作中,因此需要采用恰当的解模糊方法,以期将较为模糊的结果转变为一个较为精确的量。该模糊控制器的斥力增压K输出曲面如图4所示。

图4 斥力增压K输出曲面图Fig.4 Output surface of repulsive pressure boosting K
由图4可知,被控对象巡检机器人与障碍物之间存在互相排斥的力。这是由于进行了模糊推理,使得巡检机器人能够有效避免障碍物,进而不受干扰或影响地完成工作任务。当巡检机器人与障碍物、巡检目标点位于不同路线或环境时,其运动路径及工作时间等均会产生变化。
本文研究所进行的巡检机器人路径仿真试验结果如图5所示。
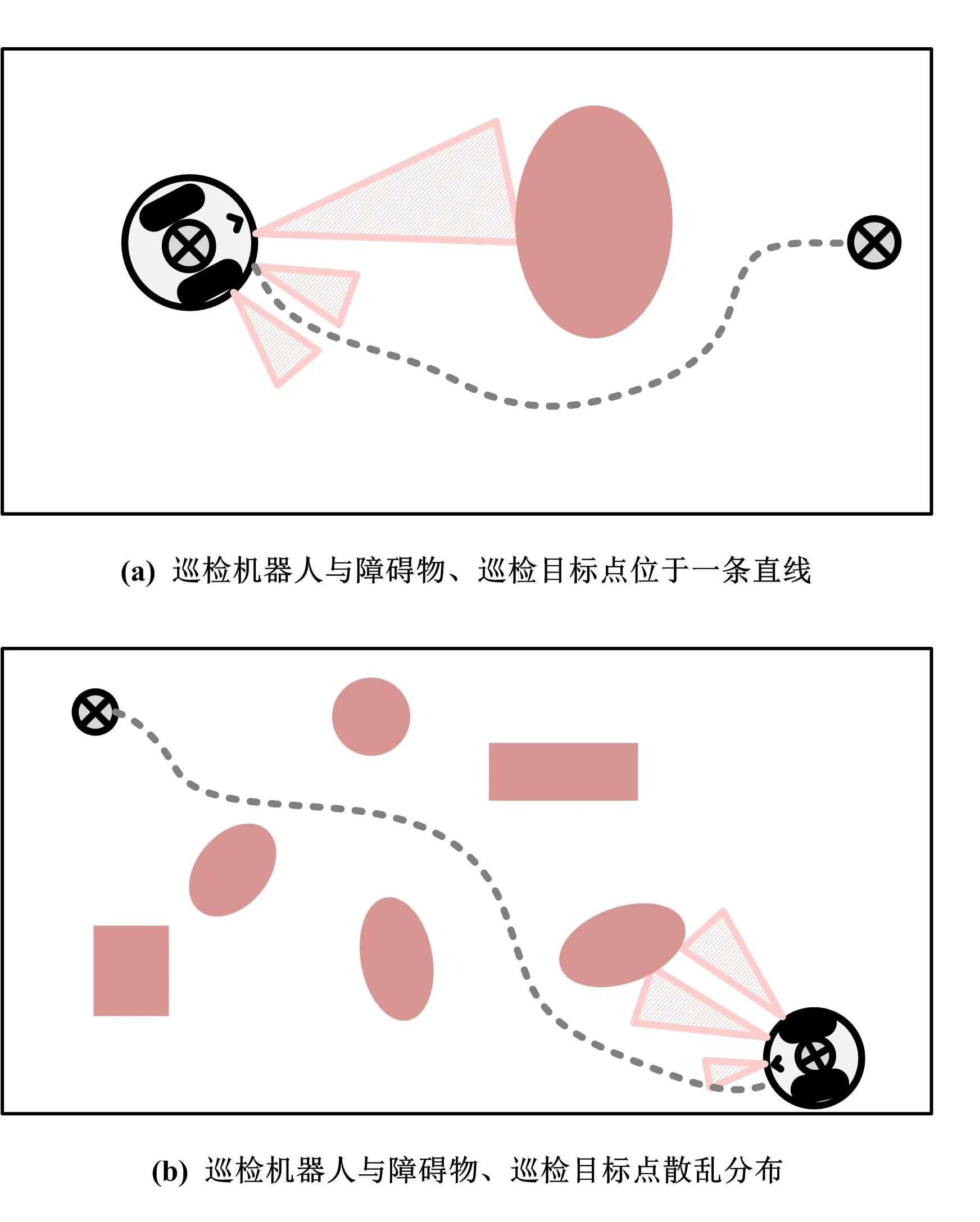
图5 巡检机器人路径仿真试验结果Fig.5 Simulation results of inspection robot path
图5(a)是巡检机器人与障碍物、巡检目标点三者位于一条直线时的情况。图5(b)则是障碍物较多且不规则出现的情况。当巡检机器人开始工作时,会受到巡检目标点对其的引力以及障碍物对其的斥力,必须在斥力的作用下进行紧急避障,改变自身的行进方向及路径,远离障碍物。巡检机器人在面临这两种情况时均能准确地对巡检目标点进行定位,并顺利完成巡检任务。为了进一步验证仿真效果,应用控制器进行仿真试验。自适应参数的仿真结果如图6所示。

图6 自适应参数的仿真结果Fig.6 Simulation results of adaptive parameters
从图6所示的仿真结果可知,当时间到达2 s左右时,系统可以达到稳定状态。使用基于卡尔曼滤波跟踪算法的巡检机器人跟踪定位技术具有较好的控制效果。该控制曲线的收敛速度较快,具有较强的鲁棒性[11]。该机器人能实现的功能主要涵盖了五个方面。①巡检机器人具有对周围所处的环境信息进行感知的能力,包括障碍物的数量、位置等。在此基础上,巡检机器人可以确定自身在智能变电站中的位置、自身的工作状态以及任务完成度等。②巡检机器人可以对导航定位信息进行处理,识别出自身与路径之间的距离和角度等关系,通过卡尔曼滤波技术进行高效且准确的导航控制,以减少完成巡检任务时的资源消耗。③巡检机器人能够控制自身完成动作行为,实时监测自身工作执行的状况,即是否完成目标巡检任务,以及在完成巡检的过程中有无差错等。④巡检机器人具有获取探测装置信息的能力,能够对检测装置进行动作控制,进而达到完成工作任务所需的位姿。⑤巡检机器人具有远程操作性,可通过控制中心远程对巡检机器人下达命令。巡检机器人在接收到工作命令后,可以立即调整行进路径和巡检目标。
4 结论
现代科学技术的持续发展,促使智能变电站的各项技术都在不断提升。为了完成智能变电站的高效、准确定位跟踪与巡检任务,进而保证电力的稳定供应,本文围绕着智能变电站定位跟踪等相关技术进行了深入的分析。本文研究通过对基于卡尔曼滤波跟踪算法的分析、对该技术的优化扩展以及相关的仿真试验等方法,得出以下研究成果。基于卡尔曼滤波跟踪算法的智能变电站定位跟踪技术具有较强的优越性,可使巡检机器人高效、准确地完成工作,维护电力设备与供应的稳定性。本文研究尽管取得了一定的成果,但仍然存在一些不足。后续研究将以更加全面、科学的仿真试验分析,进一步提升基于卡尔曼滤波算法的定位跟踪技术的性能。
