EKF和UKF在惯导初始对准中的运用
2022-01-17陈治国
陈治国
(中国空空导弹研究院,河南 洛阳 471000)
0 引言
对于惯导系统而言,滤波估计是其重要过程之一或功能实现的流程,故而非线性滤波和导航技术密切关联在一起;非线性滤波对惯导技术的发展能提供强大的动力,而导航系统性能的进步也对非线性滤波提出更多、更高的要求。当下,可供选择的非线性滤波方法较多,这样选出适用于惯导系统非线性问题的算法,或依照系统要求提出相配套的滤波算法,为国内外导航领域研究的共同问题之一[1]。
在小角度误差工况下,应用卡尔曼滤波能实现对可观测系统状态的最优估计。但若方位误差角偏大,系统模型是非线性时,推荐用EKF。因 Jacobian矩阵维数较高且存有正交项,故而增加了测算难度且错差率较高。20世纪末期,国外有学者提出UKF方法,其直接应用非线性模型,显著提升了滤波精准度。
1 EKF滤波算法
分析如下的非线性系统[2]:
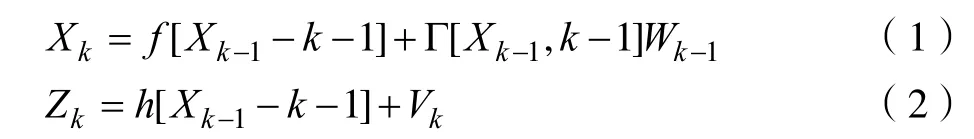
在上式内,Wk1-与kV是零均值白噪声序列,可用下式表示其统计属性:

EKF法紧扣滤波值^Xk展开非线性函数f[•]与h[•],使其成为泰勒级数且省略了去二阶以及以上项去进行线性化的方法所得的风险性系统相配套的线性化模型。其中状态方程(1)经以上操作后,有[3]:

那么状态方程可以表示成:

估测误差方差阵[4]:

2 UKF滤波算法
对于非线性系统而言:

在上式内,xk是nk维的系统状态向量,yk是ny维的系统观测向量;vk代表的系统噪声,其对应的协方差矩阵是vP。kn是观测噪声,协方差矩阵是nP。
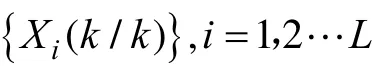

3 基于惯导系统初始对准的非线性误差模型
惯导初始对准的目标是诱导计算地理系和现实的地理系相互重合,假定两者之间的不对准角是小角度Eφ、Nφ与Uφ。那么有惯导基本方程能推导出速度误差方程[5]:

在静基座工况下,外部提供惯导系统所处地理方位的精准值,顺着计算地理系z轴方向速度是零,那么此时可简化静基座惯导初始对准系统的误差模型[6]:

可以将系统量测方程设定为[7]:

在上式内,Eη、Nη是量测噪声,设定是零均值高斯白噪声。
4 仿真分析
系统状态x的初始值x(0)取值为0,陀螺仪常值漂移的对应值是0.02(°)/h 随机漂移0.01(°)/h,三个不同方向的加速度计的原始偏差都取定为1×10–4g,随机偏差是0.5×10–4g,水位速度误差都是0.1m/s,东向、北向水平误差角与方位误差角分别是3°、2°、2°。假定静基座管道系统所处位置的地理唯独是L=45°,则有:
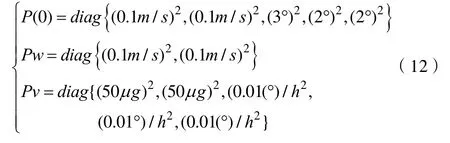
依次用EKF和UKF算法进行对准,设定仿真时间是1200s,便能顺利获得惯导系统初始对准的姿态误差角Eφ、Nφ与Uφ,并分析了以上三项指标的仿真情况[8]。不难发现,应用以上两种算法获得的估计结果十分相近,相比之下,UKF滤波法收敛速度相对较快速。
5 结语
本文在阐述 EKF、UKF算法各自原理、操作流程及优越性的基础上,把以上这两种算法分别用于惯导系统的初始对准范畴中,对比分析了仿真以后的结果,发现 EKF、UKF算法能较好的提升滤波的收敛速度。和EKF做比较,UKF算法直接应用了非线性模型,规避引进线性化误差,并且很容易实现,方法简单可靠,在处理非线性滤波问题方面能取得较好成效。
