基于复合摆线轨迹的四足机器人稳定性分析

张良安，唐 锴，李鹏飞，桂文珺，赵永杰，王孝义

(1.安徽工业大学 机械工程学院，安徽 马鞍山 243002；2.汕头大学 工学院，广东 汕头 515063)

足式机器人相较于传统的轮式和履带式机器人能够灵活调整行走时的位姿和步态，因此更适合在野外等非结构环境中进行移动[1].足式机器人一般可分为双足、四足和六足，而四足机器人由于具有较好的稳定性和较低的结构复杂度[2]，近年来成为机器人领域研究的热点之一.四足机器人常用步态主要有walk步态、trot步态、跳跃步态和奔跑步态[3]，其中由于trot步态具有快速且低功耗的特点[4]，使其被广泛应用于机器人的研究中.

研究发现四足机器人在以trot步态行走时，质心在支撑平面内的投影不总是在支撑对角线上[5]，造成机体绕支撑对角产生翻转，从而影响了机器人运行时的稳定性和可靠性.国内外学者对怎样提高四足机器人的稳定性进行了大量研究.韩宝玲等[6]针对对角步态行走过程中容易失稳的问题，提出通过改变对角步态中支撑足的初始位姿来改善运动稳定性，但未考虑其运动过程中质心波动带来的步态累积误差.雷静桃等[7]建立了具有变拓扑机构、非连续约束等特征的四足机器人非线性动力学模型，为四足机器人在非结构环境中的动态稳定性提供了参考.谢惠祥等[8]在理论分析翻转原因的基础上提出利用支撑腿的髋部侧摆关节力矩来平衡机体翻转的姿态控制方法，在一定程度上提高了四足机器人的稳定性.以上研究在不同方面对四足机器人的稳定性进行了分析，但并未进一步考虑在目标轨迹下适当调整步态周期对四足机器人稳定性的影响.因此，文中基于复合摆线轨迹对不同步态周期下的四足机器人稳定性进行研究.

为进一步提高已有四足机器人的稳定性，文中将机体翻转角作为主要性能评价指标，首先采用复合摆线法确定其目标轨迹，并结合运动学模型将得到的相关驱动函数导入到ADAMS中进行动力学仿真，然后适当调整步态周期对四足机器人的稳定性进行分析，最后用物理样机试验对结果进行验证.

1 四足机器人结构设计

参考国内外文献[9]，对四足机器人结构进行了设计，具体结构如图1所示.

图1 四足机器人结构图

所设计的四足机器人主要由机体和4条对称布置的腿部机构组成.腿部机构采用前后肘式的拓扑结构，对称布置在机体四周.其单腿具有3个转动关节，包括侧摆关节、髋关节和膝关节，并在侧摆关节和髋关节处配备减速器，以增大其驱动力矩.大腿内部电动缸做直线运动，该运动通过曲柄滑块机构带动小腿绕膝关节转动.四足机器人在直线行走时，主要通过大腿与小腿间的相互协调以及各腿部之间的连续步态来实现其运动.

2 运动学分析

由图1可知四足机器人单腿为3自由度铰链结构，运用D-H法建立其单腿D-H模型，如图2所示.

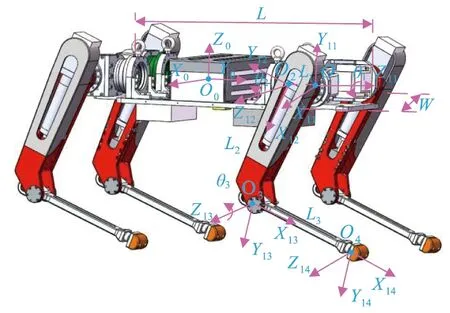
图2 四足机器人单腿D-H模型

图2中，O0X0Y0Z0、O1X11Y11Z11、O2X12Y12Z12、O3X13Y13Z13和O4X14Y14Z14分别表示机体坐标系、侧摆关节坐标系、髋关节坐标系、膝关节坐标系和足端坐标系，简称为坐标系0，1，…，4，其中坐标系0建立在机体几何中心位置.L为机体长度，W为机体宽度，θ1、θ2、θ3分别为侧摆关节转角、髋关节转角和膝关节转角，L1、L2、L3分别为髋部杆长、大腿杆长和小腿杆长.根据各坐标系间的关系列出D-H参数表，如表1所示.i为坐标系代号,i=0,1,2,3,4.

表1 D-H连杆参数表

根据齐次变换矩阵理论，坐标系{i}和其相邻坐标系{i-1}之间的D-H变换矩阵为

(1)

(2)

式中：R表示足端坐标系相对于机体坐标系的旋转矩阵；P=[PxPyPz]T表示足端在机体坐标系中的位置坐标.通过式(2)计算得到

(3)

式中：c1和s1分别表示cosθ1和sinθ1；c2和s2分别表示cosθ2和sinθ2；c23和s23分别表示cos(θ2+θ3)和sin(θ2+θ3).

为了对四足机器人进行轨迹规划和控制，对其进行逆运动学分析.通过式(3)可分别求出各关节转角函数，具体如下：

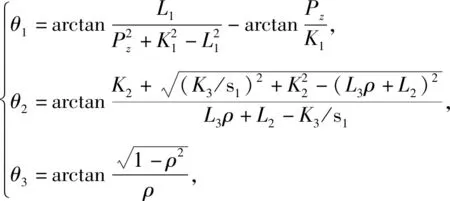
(4)

3 足端轨迹规划

文中在离线对角小跑步态下对四足机器人不同步态周期的稳定性进行研究，因此规划一条合理的、能够满足任务要求的足端轨迹显得尤为重要[10].根据一些以往的研究发现，在对四足机器人进行轨迹规划时，复合摆线轨迹能够减小足端与地面的冲击.因此，文中采用复合摆线法对其进行轨迹规划，并依据关节速度和加速度连续性要求推导出轨迹方程.

根据四足机器人完成任务要求，对步态参数进行了设置，其中步长S=0.2 m，步高h=0.08 m，单腿步态周期为T=1 s，四足机器人摆动相与支撑相在T0=T/2时进行切换，则在0～T0时段，足端处于摆动相，在T0～T时段,足端处于支撑相.设水平方向为Y0方向，竖直方向为Z0方向，足端与地面接触点为轨迹规划的起始点，且在髋关节质心正下方.机体质心到地面的高度为H=0.6 m,单腿运动时间为t，在机体坐标系中建立足端轨迹方程：Y0方向上约束方程为

y|t=0=L/2,y|t=T0=S+L/2,y|t=T=L/2,

(5)

Z0方向上约束方程为

z|t=0=-H,z|t=T/4=h-H,z|t=T/2=-H,

(6)

(7)

支撑相函数为

(8)

则整个复合摆线的运动轨迹如图3所示.

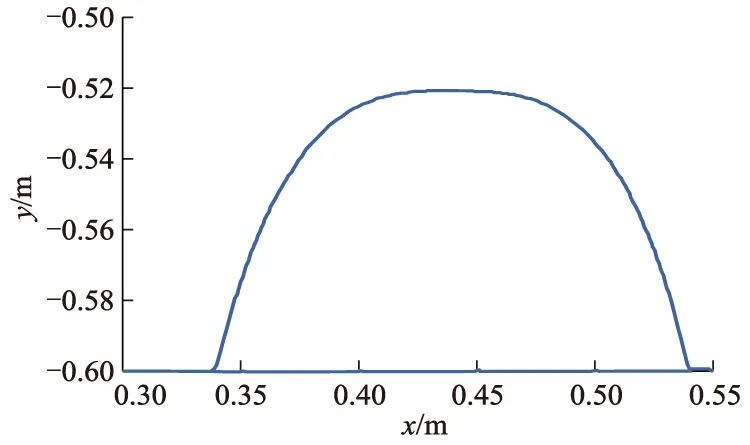
图3 复合摆线轨迹

4 仿真验证

为确保后续试验的准确性和有效性，文中对所规划的轨迹进行了仿真验证，令L1=0.12 m，L2=0.34 m，L3=0.32 m，将各步态参数和式(7)、(8)代入到式(4)中，得到各关节驱动函数，将其导入到ADAMS模型中，并设置相关约束和力以驱动机器人进行直线行走，行走过程截图如图4所示.

图4 四足机器人行走过程

通过ADAMS仿真可测得四足机器人进行直线行走时单腿各关节运动曲线，如图5所示.

图5 各关节运动曲线图

由图5可见，四足机器人在一个运动周期内速度和加速度连续，且在启动和结束时各关节加速度近似为0，减小了足端与地面的冲击，从而验证了所推导复合摆线轨迹的有效性.

5 试验分析

由文献[5]可知，四足机器人稳定性主要由机体翻转角决定，因此将机体翻转角作为主要性能评价指标，并在给定目标轨迹下通过调整步态周期来进一步提高四足机器人的稳定性.

文中以前述复合摆线轨迹作为基准，在其步态周期附近进行连续采样，随后结合式 (4)、(7)、(8)，通过MATLAB进行数值计算得到各关节驱动函数，将其导入到ADMAS模型中进行动力学仿真试验，测得不同步态周期下的四足机器人试验数据，如表2所示.

表2 不同步态周期下的四足机器人试验数据

通过表2分析可知，当四足机器人步态周期为1.3 s时，机体最大翻转角达到最小，较优化前下降1.014°，且质心(机体的几何中心)波动范围也随之减小，从而提高了四足机器人的运动稳定性，其优化前后一个周期内的机体翻转角如图6所示.

图6 优化前后机体翻转角

由图6可见，优化后机体翻转角在机体左右两侧翻转，相较于优化前机体的向一侧偏转，在一定程度上减少了步态累积误差；并且优化后机体翻转角幅值波动范围较小，也降低了机器人trot步态下足端对地面冲击.其中在0.5～0.6 s时，优化后机体翻转角波动明显是由于机体从一侧翻转到另一侧造成，但其整体幅值仍小于优化前.

为了进一步验证文中所提方法的有效性，通过物理样机对所提方法进行了验证，其具体结构参数见表3，物理样机(主材料为铝合金)行走测试过程如图7所示.

表3 四足机器人结构参数表 m

图7 物理样机trot步态下的行走过程

测试结果表明，优化前四足机器人物理样机在行走到第87个步态周期后机身开始出现明显抖动，而优化后机器人在行走到第132个步态周期后机身才开始出现明显抖动.这进一步证明了当四足机器人在给定目标轨迹下，通过适当调整步态周期可使机体最大翻转角降低，且保持在一个较小的范围内波动，从而有效减小了步态累积误差，提高了四足机器人的稳定性.

6 结 论

1)为提高四足机器人的稳定性，文中基于复合摆线对不同步态周期下的四足机器人稳定性进行了研究，并将机体翻转角作为主要性能评价指标，通过仿真和物理样机试验对所提方法进行了验证.

2)采用复合摆线法对四足机器人进行了轨迹规划，并结合运动学模型得到各关节驱动函数，将其导入到ADAMS进行动力学仿真，验证了轨迹规划的有效性.

3)基于给定目标轨迹，通过适当调整步态周期对四足机器人的稳定性进行了分析，试验结果表明在一定的范围内适当整步态周期可提高其运动稳定性，从而验证了文中所提方法的有效性.