泥岩掉块层位还原技术研究与应用

2022-01-16王建立刘少峰李亚男

录井工程 2021年4期

丁冬王建立陈卓刘少峰李亚男

(①中海油能源发展股份有限公司工程技术分公司；②中海石油(中国)有限公司天津分公司)

0 引言

锦州25油田位于渤海辽东湾中部海域，是一个有利的油气成藏区带[1-3]，受作业条件的限制，开发井以大位移井为主[4]，且东营组普遍发育厚层泥岩，斜深厚度平均为1 000 m。该油田东营组泥岩以湖相、深湖相沉积为主，时间跨度为23～32 Ma，同时受构造运动、沉积速率的影响，泥岩的矿物成分存在差异，但岩屑录井反映的是灰色、深灰色泥岩，测井曲线近乎直线状，难以区分不同井段泥岩的差异性。

在钻井作业中东营组泥岩地层井壁坍塌失稳现象频发[5-6]，造成了多口井起下钻困难、卡钻等复杂情况。钻井现场一般通过循环、捞样，肉眼观察泥岩掉块的大小及数量，凭借经验，根据泥岩掉块的颜色及形状等判断井壁失稳层位及程度，进而优化钻井液性能及井身结构等，但效果参差不齐，影响了钻井安全和时效。

在地质工程一体化理念的指引下[7]，笔者在钻井需求和录井、测井技术特点结合的基础上，提出了利用元素录井获取泥岩段和掉块的矿物成分，并借助数学算法的快速处理能力，实现了定量化、智能化地快速还原泥岩掉块深度，从而确定坍塌井段位置和程度，为钻井施工方案提供数据支持。本方法在锦州25油田得到成功应用，为其他油田高效钻井施工提供借鉴，为渤海油田上产4 000×104t积淀技术。

1 研究思路

本文以锦州25油田为靶区，将元素录井与数学算法有效结合，形成了一套泥岩掉块层位还原的判定流程(图1)，最终实现坍塌井段及坍塌程度的识别评价，为工程方案制定提供数据支撑。其具体研究思路可分为以下五部分：

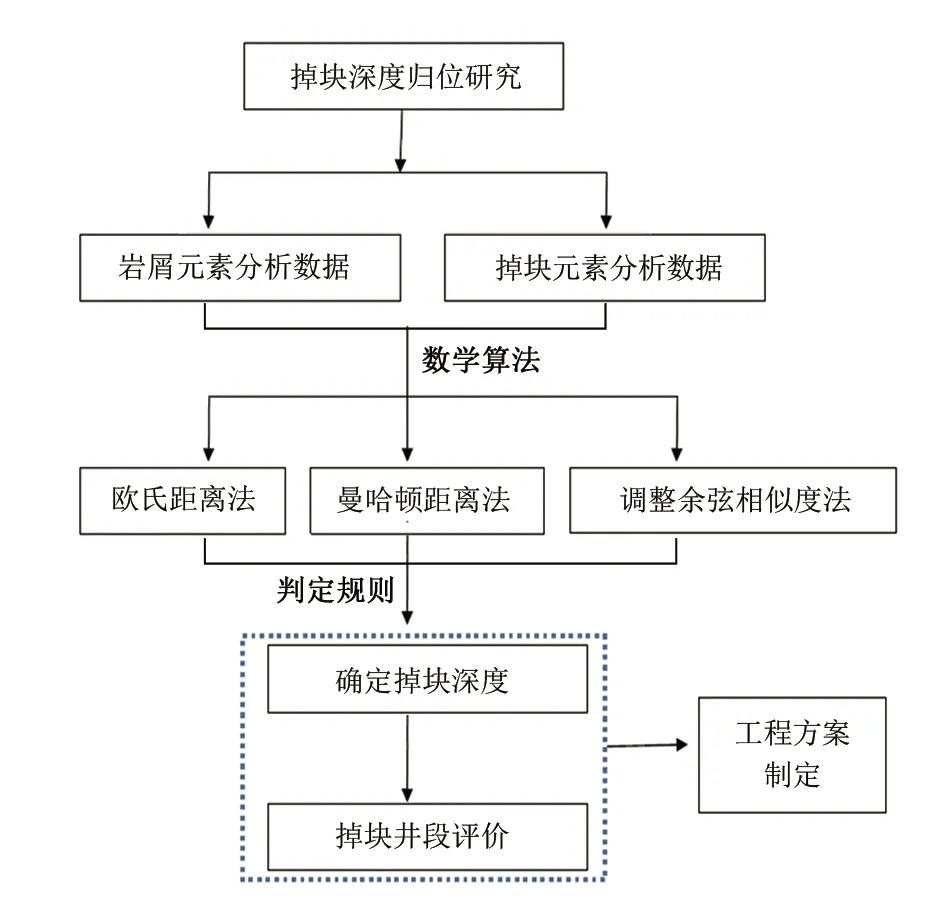
图1 泥岩掉块层位还原流程

(1)采集全井段岩屑元素录井数据，创建单井元素地层剖面。

(2)收集掉块并进行元素录井数据采集。

(3)利用数学算法计算掉块深度，实现定量化确定掉块层位还原。

(4)根据掉块的分布情况确定坍塌井段并进行坍塌程度评价。

(5)制定合理的工程施工方案。

2 地层信息获取

2.1 全井元素数据分析

根据地质设计要求的取样间隔捞取岩屑样品，按照元素录井操作流程将样品进行烘干、粉碎、压片、分析[8]，以获取原始元素录井剖面数据，如锦州25油田X 1井(表1)，此过程需确保岩屑数据的全面性及准确性，从而建立起基于矿物成分的泥岩段元素剖面。

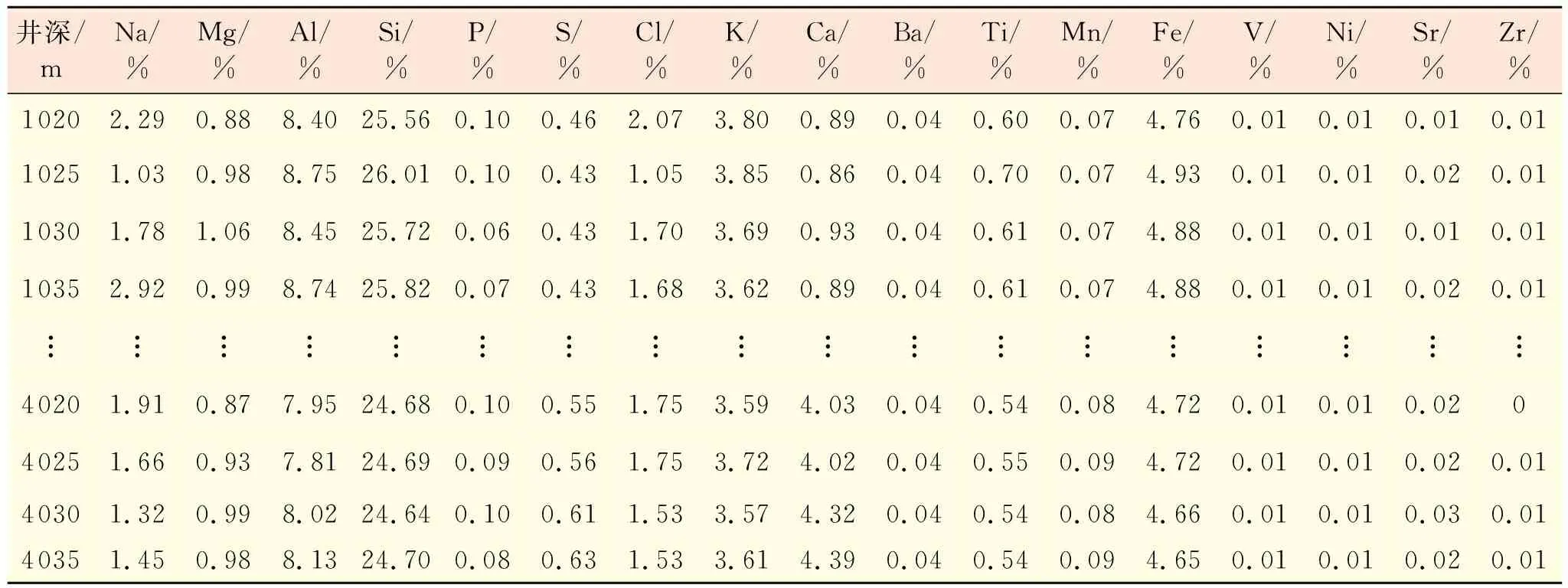
表1 锦州25油田X 1井元素数据

2.2 泥岩掉块元素分析

不同油田由于其泥岩段失稳程度差异，地层破碎程度也存在一定差异，返出泥岩掉块大小、形态也呈现不同的特征(图2)。为准确地对失稳性泥岩掉块进行归位，掉块取样要求为：(1)以钻井液单次循环返出的掉块为一深度单元；(2)泥岩掉块大小超过2 cm×2 cm×1 cm可直接对单个掉块取样分析；(3)对掉块小于2 cm×2 cm×1 cm，选取颜色一致、磨圆度相近的多个掉块同时分析。取样结束后，按元素录井操作流程对样品进行处理、分析，最终获取泥岩掉块的元素数据。

图2 失稳性泥岩掉块

3 泥岩掉块归位精准分析模型

3.1 数据归一化

为了提高模型的收敛速度，避免不同元素值的绝对值差异影响数据分析结果，对元素数据进行归一化处理。本文采取的归一化处理方法为将某一样品的特定元素除以该样品所有元素和，形成新的元素数据值，处理后该样品单个深度点的所有元素值总和为1。

(1)

式中：Xi′为第i个元素的归一化元素值；Xi为第i个元素的初始元素值；n为样品含有的元素数量。

3.2 基于相似度评价的数学模型

相似度评价法是运用模糊综合评判原理[9]，根据数据与标准值的相似度来评价个体间的差异大小。为提高数据分析的可靠性，本文同时引入3种常见的相似度评价算法(欧氏距离法、曼哈顿距离法、调整余弦相似度法)分析样本之间的相似性。

3.2.1 欧氏距离法

欧氏距离是指在多维空间向量中两点之间的距离，当两个样品的元素值在空间距离越短时，判定这两个样品之间的相似度越高，其公式如下：

(2)

式中：d1kl为第k个掉块样品元素值与第l个全井样品元素值之间的欧氏距离；Xi′k为第k个掉块样品的第i个元素的归一化元素值；Xi′l为第l个全井样品的第i个元素的归一化元素值。

当d1kl最小时，第k个掉块样品和第l个全井样品最为相似，那么第k个掉块的深度可归位为第l个全井样品的深度。

3.2.2 曼哈顿距离法

与欧氏距离相似，曼哈顿距离表征掉块样品与全井样品相同元素之间的距离绝对值，所有元素的距离绝对值累加之和即为曼哈顿距离，当曼哈顿距离最小时，判定两个样品最为相似，其公式如下：

(3)

式中：d2kl为第k个掉块样品元素值与第l个全井样品元素值之间的曼哈顿距离。

当d2kl最小时，第k个掉块样品和第l个全井样品最为相似，那么第k个掉块的深度可归位为第l个全井样品的深度。

3.2.3 调整余弦相似度法

调整余弦相似度法是用向量空间中两个向量夹角的余弦值作为衡量两个样本差异大小的度量。两个样本向量的夹角余弦值越接近于1，两个样本越相似，其公式如下：

(4)

式中：d3kl为第k个掉块样品元素值与第l个全井样品元素值之间的夹角余弦值。

当d3kl越接近于1时，第k个掉块样品和第l个全井样品最为相似，那么第k个掉块的深度可归位为第l个全井样品的深度。

3.3 深度确定准则

通过引入欧氏距离等3种数学算法，可以获得某一掉块的3个计算深度，利用表2中的匹配准则来确定掉块最终的匹配深度：(1)当3种算法所计算的深度为同一值，掉块匹配深度就为该深度值；(2)当有两种算法所计算的深度一致，另外一种算法计算深度不一致时，掉块匹配深度取两种算法一致的深度；(3)当3种算法所计算的深度各不相同时，对该掉块深度不予深度判定，认为该掉块分析数据超出了正常录井要求的岩屑分析段。

表2 掉块深度判定规则

为更加直观利用掉块深度位置评判井壁失稳井段和失稳程度，建立了掉块深度归位图，如图3所示，从纵向上可快速、简洁进行井眼实时评价，及时为钻井施工及其方案制定提供依据，提高作业效率。

图3 掉块深度归位图

4 应用效果

在使用元素录井和数学算法相结合实时还原泥岩掉块深度方法前，锦州25油田已钻5口井的钻井工期与设计相比平均滞后2.3 d；在应用该方法后，通过实时还原泥岩掉块，并准确对井壁失稳程度做出判断，及时调整施工方案，在该油田新钻探4口井的钻井工期与设计相比平均提前1.2 d，表明该方法在本油田应用中发挥了应有作用。

利用欧氏距离法等3种模型分别对锦州25油田A 1井和A 2井泥岩掉块进行层位还原(表3)，从表中数据可以看出，A 1井10个泥岩掉块中有效还原9个深度点，在2 965～2 990 m井段泥岩掉块占比达67%；A 2井8个泥岩掉块中有效还原8个深度点，掉块还原深度分布较为分散。A 1井泥岩掉块集中于2 965～2 990 m井段，说明该井段井壁坍塌较为严重，不满足继续钻进的条件，需要尽快中完；A 2井掉块比较分散，现场需要适当增加钻井液密度及短起钻频次，从而防止井壁失稳进一步扩大，支持继续正常钻进。