中低速磁浮列车速度对直线感应电机牵引力影响

王 滢，刘学龙，刘方麟，刘世杰，陈绍宗，卢卫国

（西南交通大学磁浮技术与磁浮列车教育部重点实验室，四川成都611756）

磁浮列车牵引力主要由直线电机产生，该电机结构通常被认为是由普通旋转电机剖分延展而形成的。中低速磁浮列车一般采用短定子直线感应电机（LIM）。LIM的直线开断结构不可避免地产生端部效应，并且随着运行速度的提高，电机涡流阻力增大，电磁推力减小，不能满足高速状态下的牵引力要求［1］。为研究中低速磁浮列车用LIM的特性，徐伟等［2］利用绕组函数法求解初级、次级的电机参数，建立电路方程以分析LIM不同速度下的推力特性；邓江明等［3］基于场路复功率相等建立LIM的T型等效电路，分析了速度与推力的关系。然而，上述文献均未考虑气隙磁场与速度畸变的关系。张宏等［4］通过理想数学模型定性分析了高速状态下LIM的端部效应，但未考虑LIM实际应用中初级双层叠绕式绕组的端部半填充槽结构产生的影响，而且未定量分析端部效应产生的涡流对牵引力的影响。

基于电磁场理论推导LIM的气隙磁场方程，研究速度对LIM牵引力的影响，并与端部全填充槽LIM进行对比，为改善电机的性能以及高速化应用提供理论基础。

1 LIM气隙磁场模型

1.1 模型建立

以中低速磁浮列车用LIM为原型，建立初级双层叠绕式绕组、端部为半填充槽结构的LIM模型（见图1）。半填充槽LIM分成5个区域，区域1为入口区域，区域5为出口区域，区域2、区域4为“半填充槽”的正对区域，长度均为Y1，区域3为电机的全填充槽结构主体区域。图1中，2pτ+Y1为LIM初级总长度，τ为电机极距，p为极对数，δ为电机气隙，d为次级感应板厚度，vx为列车运行速度。

电机初级绕组正对的次级感应板区域被称为有效区域（包括区域2、区域3、区域4）。采用准一维理论进行建模分析，作出如下假设［5］：

（1）各场量都是时间的正弦函数。

（2）初级铁芯相对磁导率无限大，即不考虑铁芯磁场饱和的影响。

（3）行波电流层代替初级绕组，初级绕组的磁动势在空间正弦分布。

（4）初级和次级电流只有z轴分量。

（5）次级感应板材料各向同性。

考虑到初级齿槽效应和气隙漏磁通的影响，分别用卡氏系数Kc、系数Kl对气隙长度进行修正；考虑到次级感应板电流集肤效应的影响，引入修正系数kf，使次级体电导率进一步减小［6］。因此，等效气隙长度δ′=KlKcδ，等效次级体电导率σe=σd/kfδ′，其中σ为次级体电导率。

由文献［7-8］中对瞬态涡流场的分析可知，低频电机磁场可作为一个准静态磁场。由于电机的初级电流频率较低，可不考虑位移电流。符合短定子LIM理论分析的麦克斯韦方程组［9］为

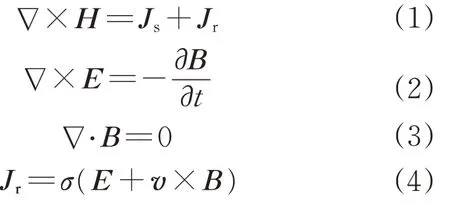
式中：H为磁场强度；Js为初级体电流密度；Jr为次级体电流密度；E为电场强度；B为磁感应强度；v为次级相对于初级的速度。

磁势的线密度即为电流面密度，所以初级绕组的电流面密度

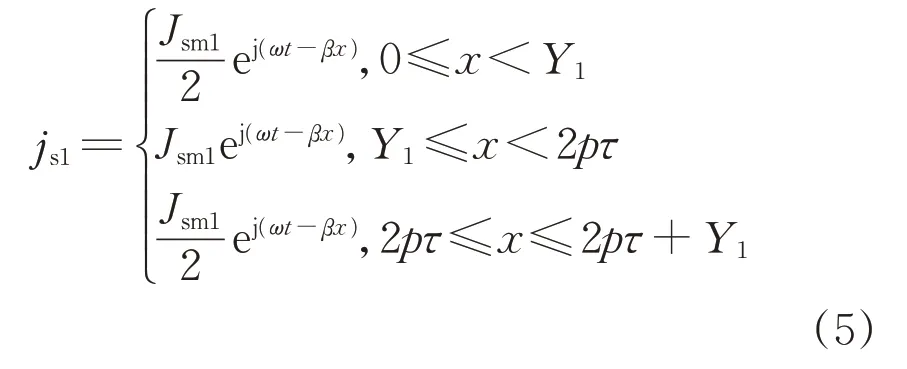
式中：Jsm1为次级体电流密度幅值；β=π/τ；ω为初级绕组电流频率。将式（4）和式（5）代入式（1），得到区域2（0≤x＜Y1)和区域4(2pτ≤x≤2pτ+Y1）的气隙磁场表达式，如下所示：

式中：Hy为磁场强度的y轴分量；μ0为真空磁导率。区域3(Y1≤x＜2pτ)的气隙磁场满足下式：

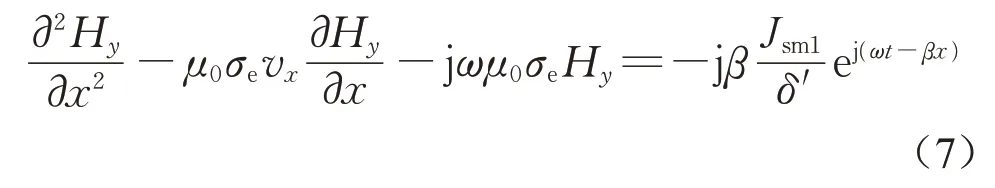
1.2 模型求解

式（6）和式（7）的特征方程相同，故有相同的特征根γ1和γ2。式（6）和式（7）的特解分别为

式中：Hy1、Hy2、Hy3、Hy4、Hy5分别为区域1、区域2、区域3、区域4、区域5的磁场强度y轴分量；M1、M2、M3、M4、M5、M6、M7、M8为待定系数。

根据磁场强度和次级体电流密度在x=0、x=Y1、x=2pτ、x=2pτ+Y1处连续的边界条件，可以得到8个方程，如下所示：

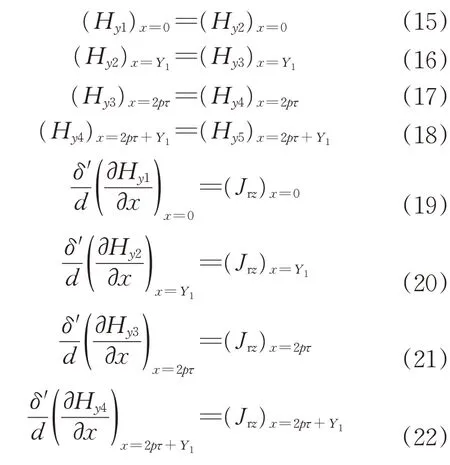
式中：Jrz为次级体电流密度z轴分量。联立式（15）～（22），得到各待定系数，如下所示：

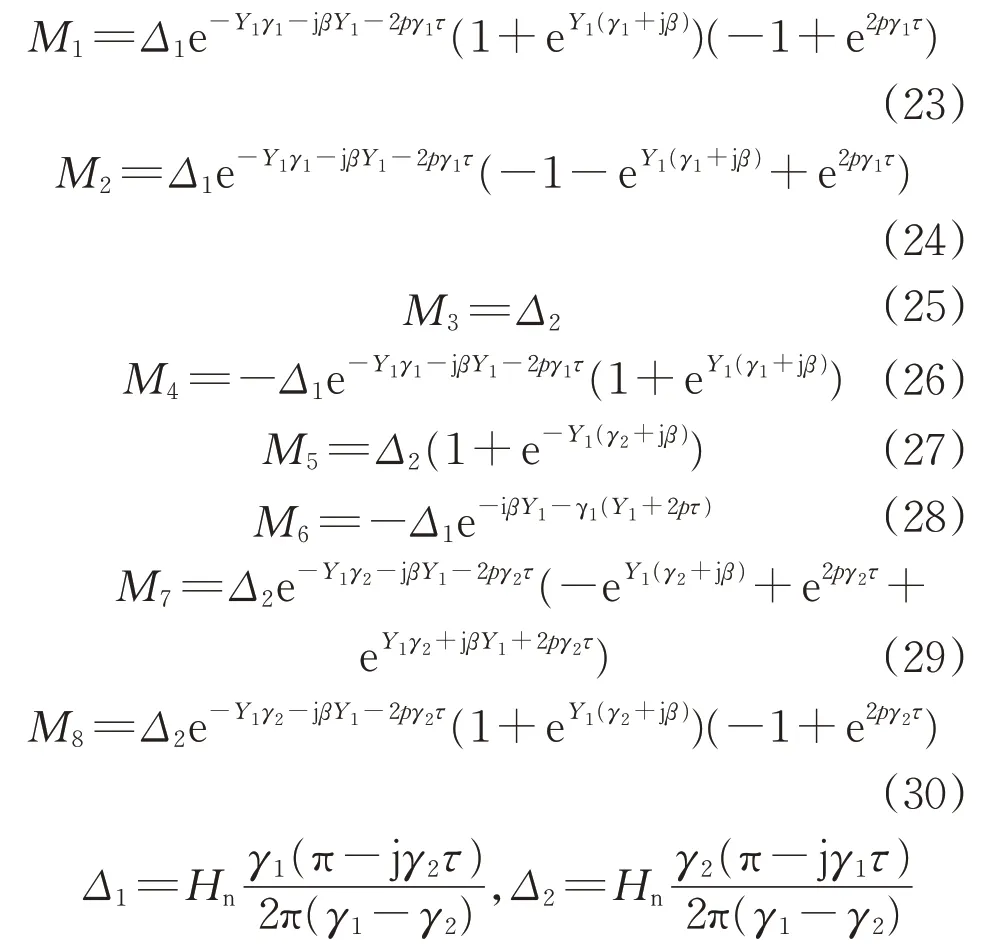
将所求系数分别代入式（10）～（14），可以得到各区域的一维气隙磁场解析表达式。

2 速度对LIM气隙磁场的影响分析

图2为中低速磁浮列车所用的LIM，该电机的结构参数如表1所示。

图2 中低速磁浮列车用LIMFig.2 LIM on medium-low speed maglev train

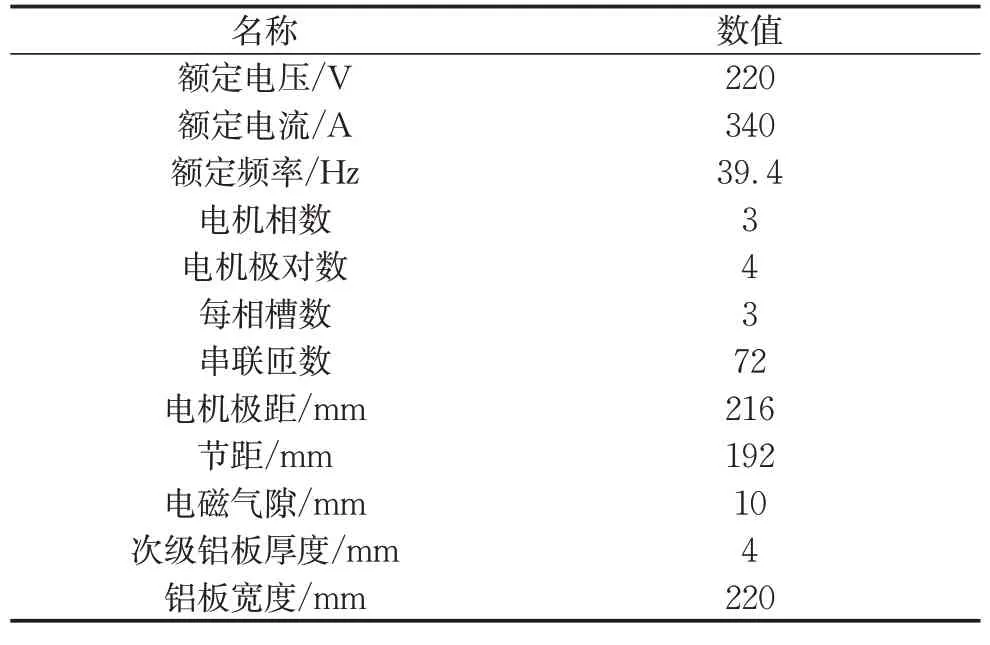
表1 LIM结构参数Tab.1 Structural parameters of LIM

2.1 一维气隙磁场分析

LIM的开断结构，使得气隙中既存在正常的行波磁场，也存在附加磁场［9-10］。附加磁场对电机的影响称为端部效应。文献［11］中对端部效应做了详细的划分，电机运动过程中入端区域和出端区域的电瞬态现象被称为纵向动态端部效应。根据式（11）～（13）可知，有效区域的气隙磁场解析式由ejωt+γ1x、ejωt+γ2x、ej(ωt-βx)3种模态组成，其中第一项为后退端部效应波、第二项为前进端部效应波、第三项为初级激励产生的正常行波。以电机运行速度100 km·h-1、初级电流有效值189 A的半填充槽LIM为例，根据式（10）～（14）给出区域1到区域5的一维气隙磁感应强度曲线，如图3所示。

从图3b可知，半填充槽LIM在速度为100 km·h-1时有效区域气隙磁场发生畸变，LIM出端区域磁场明显增强，并沿电机运动的反方向衰减，该部分行波磁场又称拖尾效应波。拖尾效应波是由初级行波磁场向前运动时在次级感应板上产生的涡流效应所致。由解析式和图3a可知，区域3内后退端部效应波从出端侧侵入有效区域约10 mm左右，对正常行波的影响较小；区域3内的前进端部效应波与正常行波波长相近、相位相反，使得前进端部效应波削弱正常行波。拖尾效应波增强延续了电机出端区域气隙磁场，最终形成电机整体气隙磁场的畸变。

2.2 速度对端部效应的影响

由于前进端部效应波对气隙磁场端部效应波的影响较大，因此进一步研究速度与前进端部效应波的关系。根据式（12）并结合图3a可知，某时刻有效区域内前进端部效应波是一束振荡衰减波，其数学表达式为M5eγ2x。因此，气隙磁场特征方程根γ2的虚部决定着前进端部效应波的半波长le=π/|Im(γ2)|。Im(γ2)计算式如下所示：

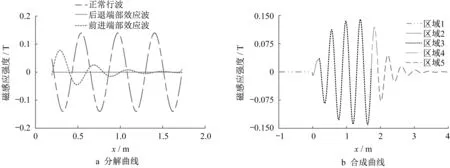
图3 半填充槽LIM的一维气隙磁感应强度Fig.3 One-dimensional air-gap flux density of half-filled slot for LIM

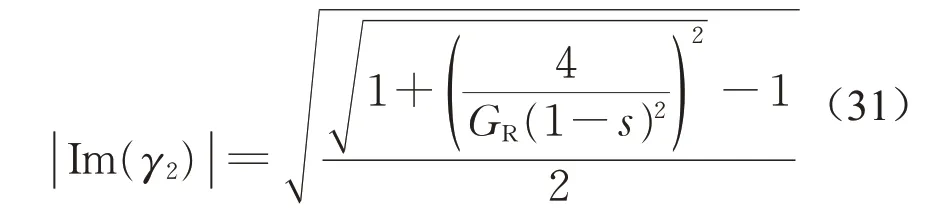
式中：GR=G/kfKlKc，其中G为实际品质因数。气隙磁场前进端部效应波系数与特征方程根γ2的实部共同决定着前进端部效应波的影响范围Re，如下所示：

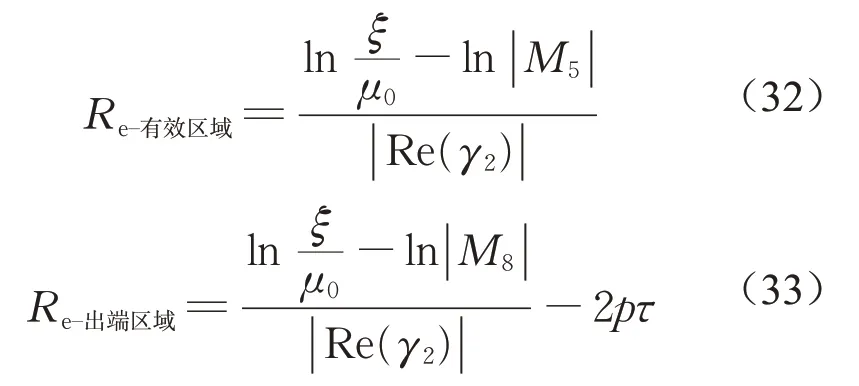
式中：ξ为大于零的最小常数，ξ=10-4。

当LIM运行速度为160 km·h-1时，前进端部效应波的半波长le=0.206 m，略小于电机极距τ=0.216 m。前进端部效应波半波长le、影响范围Re随速度的变化如图4所示，前进端部效应波的半波长随着速度增大先快速减小后增大。当速度大于90 km·h-1后，前进端部效应波的半波长逐渐增大，并且逐渐逼近电机极距τ，而前进端部效应波的影响范围随速度呈近似线性增加。由此可见，当LIM高速运行时，在有效区域内靠近入端的2个极距范围内，有效区域的正常行波磁场将被前进端部效应波削弱，直线电机的第一对极对总的牵引力贡献较小。

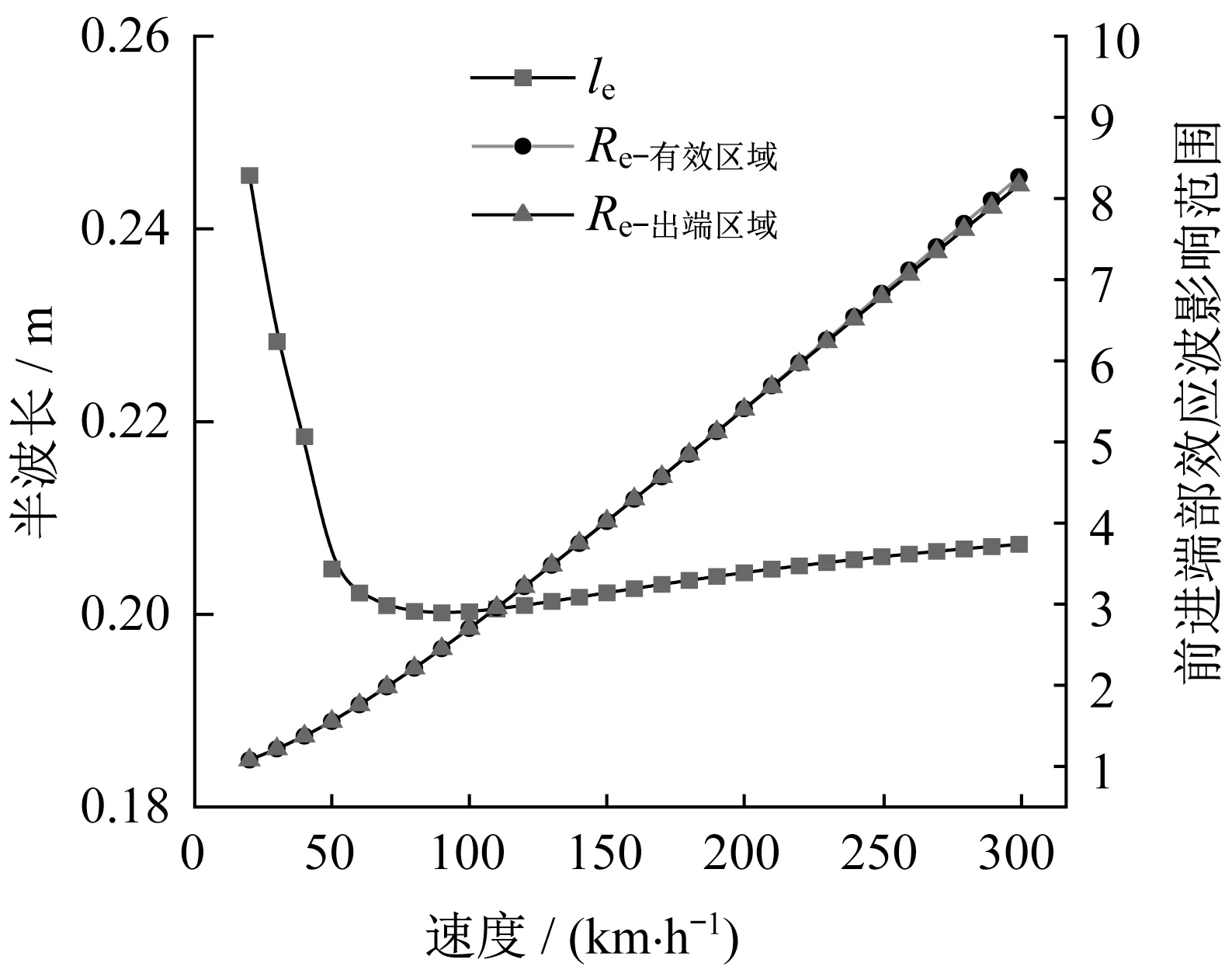
图4 前进端部效应波半波长和影响范围随速度的变化Fig.4 Variation of half-wavelength and influence range of LDEE with speed

为了对比LIM初级绕组端部半填充槽和全填充槽的动态端部效应特性，结合文献［12］对全填充槽LIM磁场的分析，用kγ表示2种填充槽结构LIM有效区域的前进端部效应系数之比，如下所示：

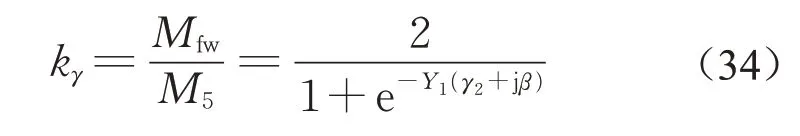
式中：Mfw为全填充槽LIM有效区域气隙磁场的前进端部效应系数。式（34）表明，kγ的取值与半填充槽区域宽度Y1直接相关，临界情况下Y1=0、kγ=1，即端部半填充槽区域宽度趋于零时，全填充槽和半填充槽的端部效应影响一致，进一步验证了气隙磁场数学模型的正确性。

图5给出了kγ与速度之间的关系。kγ随着速度增加而逐渐增大，表明全填充槽LIM的前进端部效应波系数提升幅度更大，致使kγ逐渐增大。然而，kγ的值始终小于1，说明高速时半填充槽结构LIM受端部效应的影响仍然比全填充槽结构LIM更大。

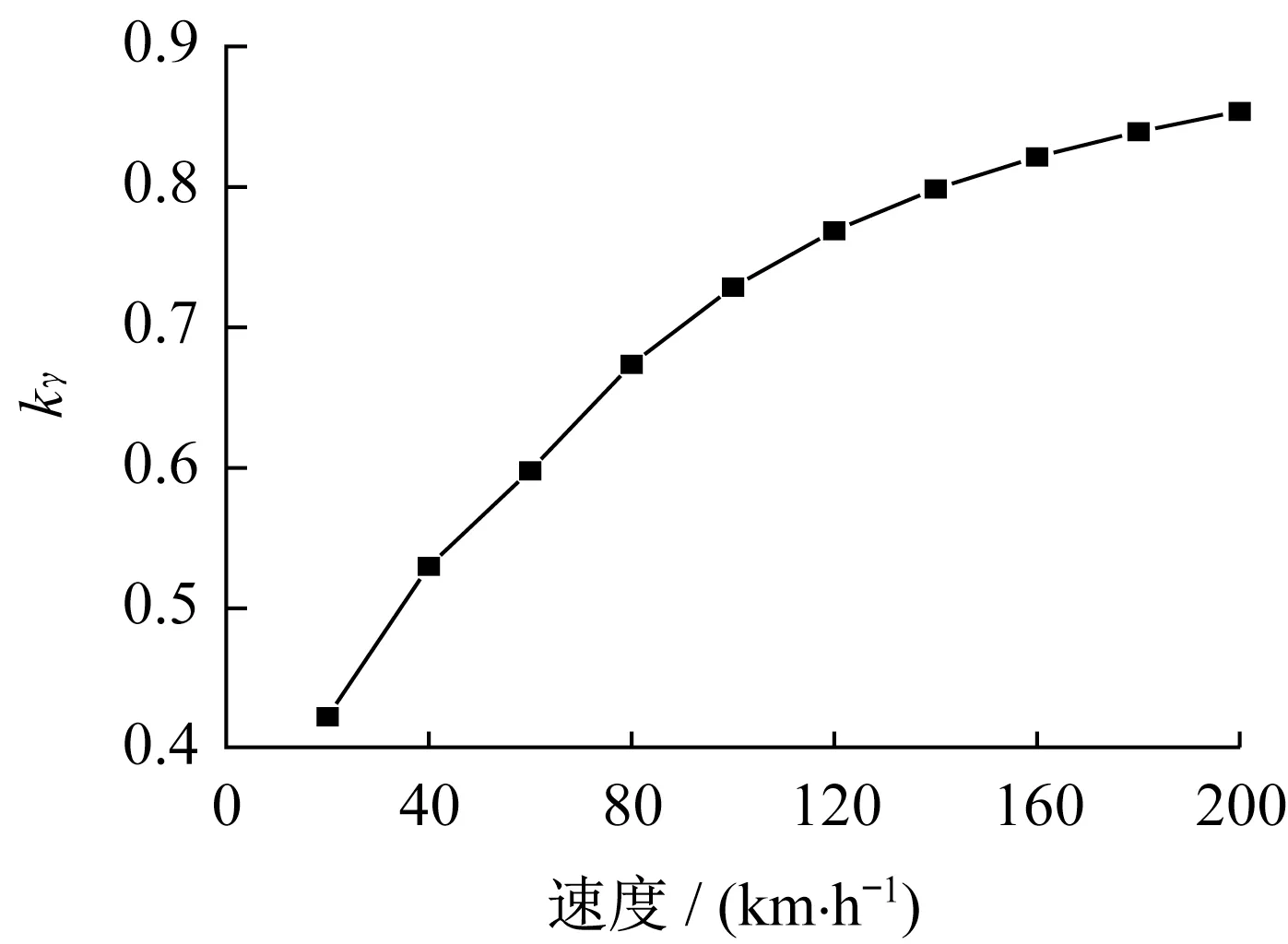
图5 kγ随速度变化Fig.5 Variation of kγwith speed

3 速度对LIM牵引力的有限元仿真分析

结合表1中的结构数据，建立有限元分析模型，如图6所示。图6中，a表示电机定子铁芯厚度的一半。在仿真分析中，设置次级感应板相对初级运动，以初级左侧为原点建立坐标系。电机初级范围为0～1.728 m。结合文献［13］对单边LIM的滑差频率优化控制研究，采用恒电流、恒转差频率策略，在仿真中采用的转差频率为13.5 Hz，同时考虑到高速情况下端压过高等因素，将初级绕组电流设置为189 A。

图6 LIM三维模型Fig.6 Three-dimensional model of LIM

3.1 气隙磁场

根据第2节分析可知，中低速磁浮列车高速运动时，气隙磁场受动态端部效应影响而产生畸变，导致牵引力减小。如图7所示，结合表1中低速磁浮列车LIM结构参数，分析速度为20 km·h-1、60 km·h-1、100 km·h-1和160 km·h-1时的气隙磁场分布。

根据图7分析可知，仅在电机入端区域仿真结果与解析结果存在细微差别，整体气隙磁场仿真结果与解析结果拟合度较高，由此验证上述数学模型的有效性。电机出端区域磁场范围和幅值随速度增加而增加，电机入端区域磁场幅值随速度增加而减小。列车高速运行时，入端区域磁场被削弱而出端区域磁场被增强，使得整体气隙磁场发生畸变。

3.2 次级涡流

为了进一步说明速度与纵向动态端部效应的关系，在距离电机入端1 m处的次级感应板上，沿纵向作长度为5 m的采样线，并以速度为20 km·h-1和100 km·h-1的次级感应板涡流为例进行说明。图8为vx=20 km·h-1、t=0.396 s时的LIM感应板涡流曲线。图9为vx=100 km·h-1、t=0.150 s时的LIM感应板涡流曲线。

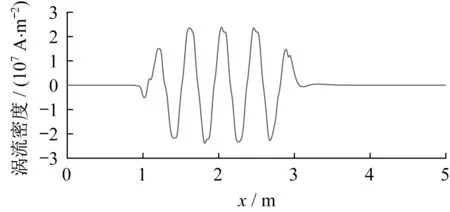
图8 vx=20 km·h-1时感应板涡流密度Fig.8 Eddy current density when vx=20 km·h-1

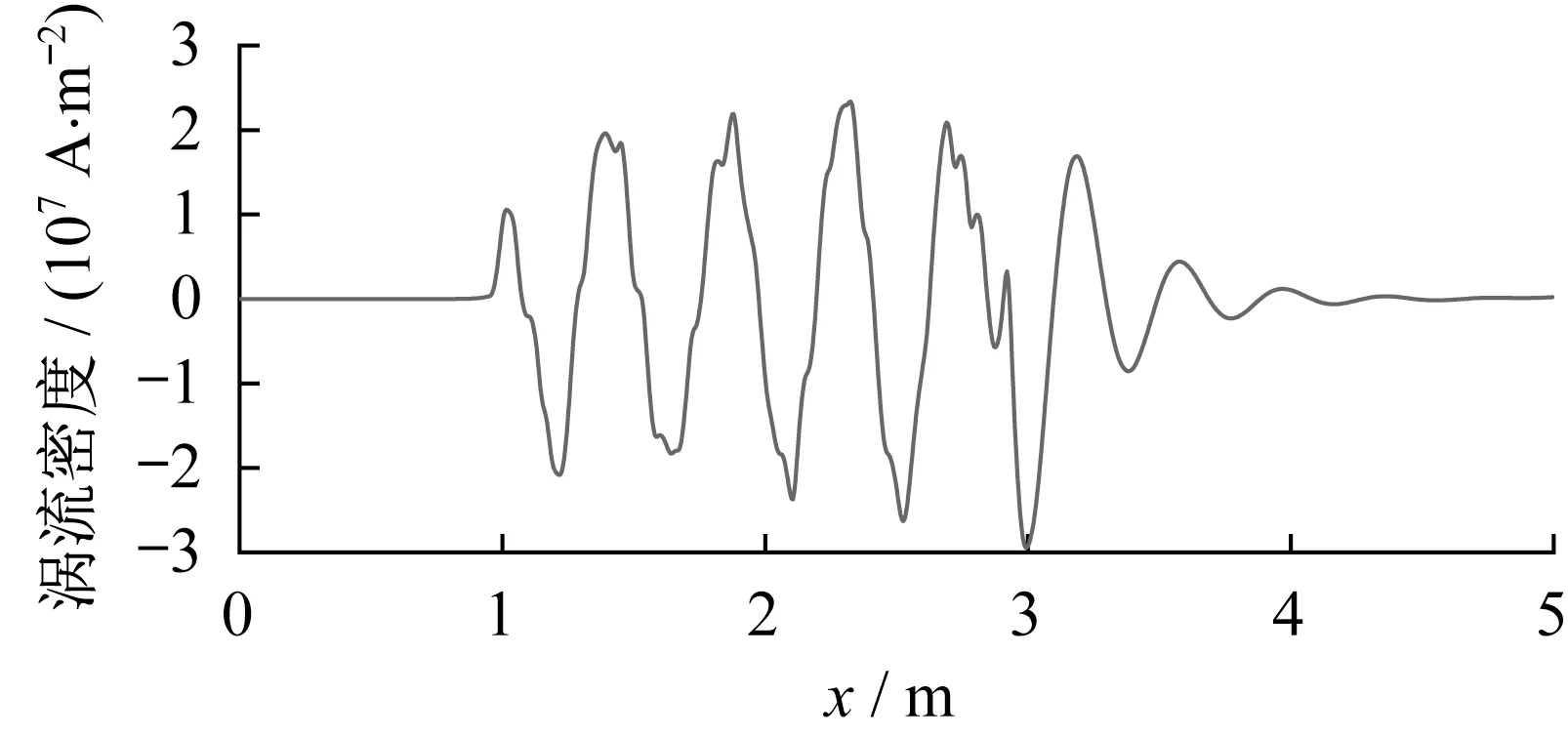
图9 vx=100 km·h-1时感应板涡流密度Fig.9 Eddy current density when vx=100 km·h-1

100 km·h-1时感应板上出端涡流范围明显比速度为20 km·h-1时的更大。LIM的涡流范围随着速度的增加而增加，导致电机的涡流损耗、铁损增加，电机的输出功率随之减小。

3.3 牵引力

图10给出了不同速度下牵引力仿真结果，并与通过气隙磁场和初级体电流密度求得的解析结果进行比较。在恒电流、恒转差频率控制下，随着速度的增加，LIM的牵引力逐渐下降。因为后退端部效应波对于电机有效区域的透入深度较小，所以有效区域内后退端部效应波基本不起作用。端部效应波力为电机有效区域内前进端部效应波产生的电磁力，该力随速度增加而增加。根据上述分析，LIM高速运行时，电机入端区域的磁场被前进端部效应波削弱而导致整体气隙磁场发生畸变，使得端部效应产生的电磁阻力逐渐增大，电机整体牵引力下降。

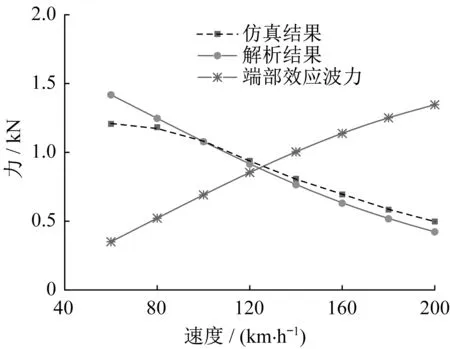
图10 不同运行速度下牵引力和端部效应波力Fig.10 Traction and end effect wave forces at different operating speeds

为了对比半填充槽LIM和全填充槽LIM的牵引力随速度变化情况，仿真了恒电流、恒转差频率时2种填充槽结构的LIM在不同速度下的牵引力。图11为电流120 A、滑差频率13.5 Hz时2种填充槽LIM牵引力随速度的变化。

由图11可知，半填充槽LIM牵引力始终小于全填充槽LIM，但速度在40～100 km·h-1时，两者牵引力差距相对较小。因此，为了横向比较半填充槽LIM和全填充槽LIM在不同速度下的牵引力减小程度，引入端部半填充槽结构的LIM相对于全填充槽结构的牵引力下降系数，计算式如下所示：

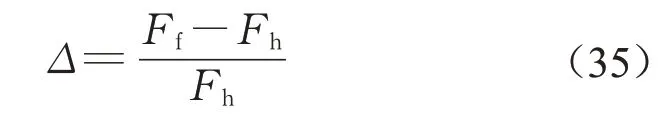
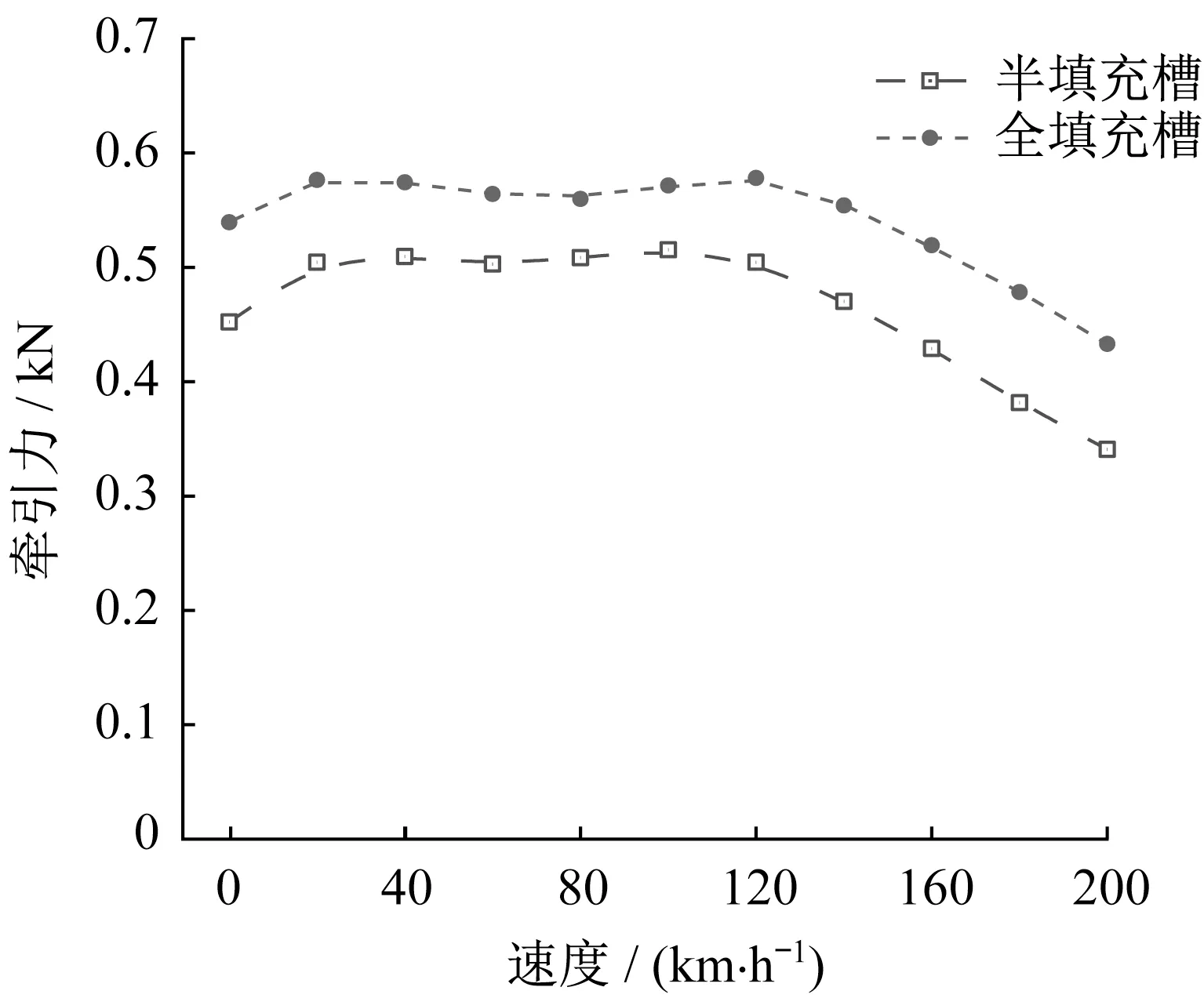
图11 2种端部填充槽LIM牵引力Fig.11 Traction of LIM for two end filled slots

式中：Ff、Fh分别为全填充槽LIM、半填充槽LIM在相同速度下的牵引力。考虑到列车实际运行时，电流并非恒定值，结合工况选取初级电流120 A、189 A和340 A进行仿真。由图12中Δ与速度的变化曲线可知，3种绕组电流趋势基本一致。半填充槽LIM在低速和高速下牵引力下降幅度相对较大，而在速度约为80 km·h-1时牵引力下降幅度最小。

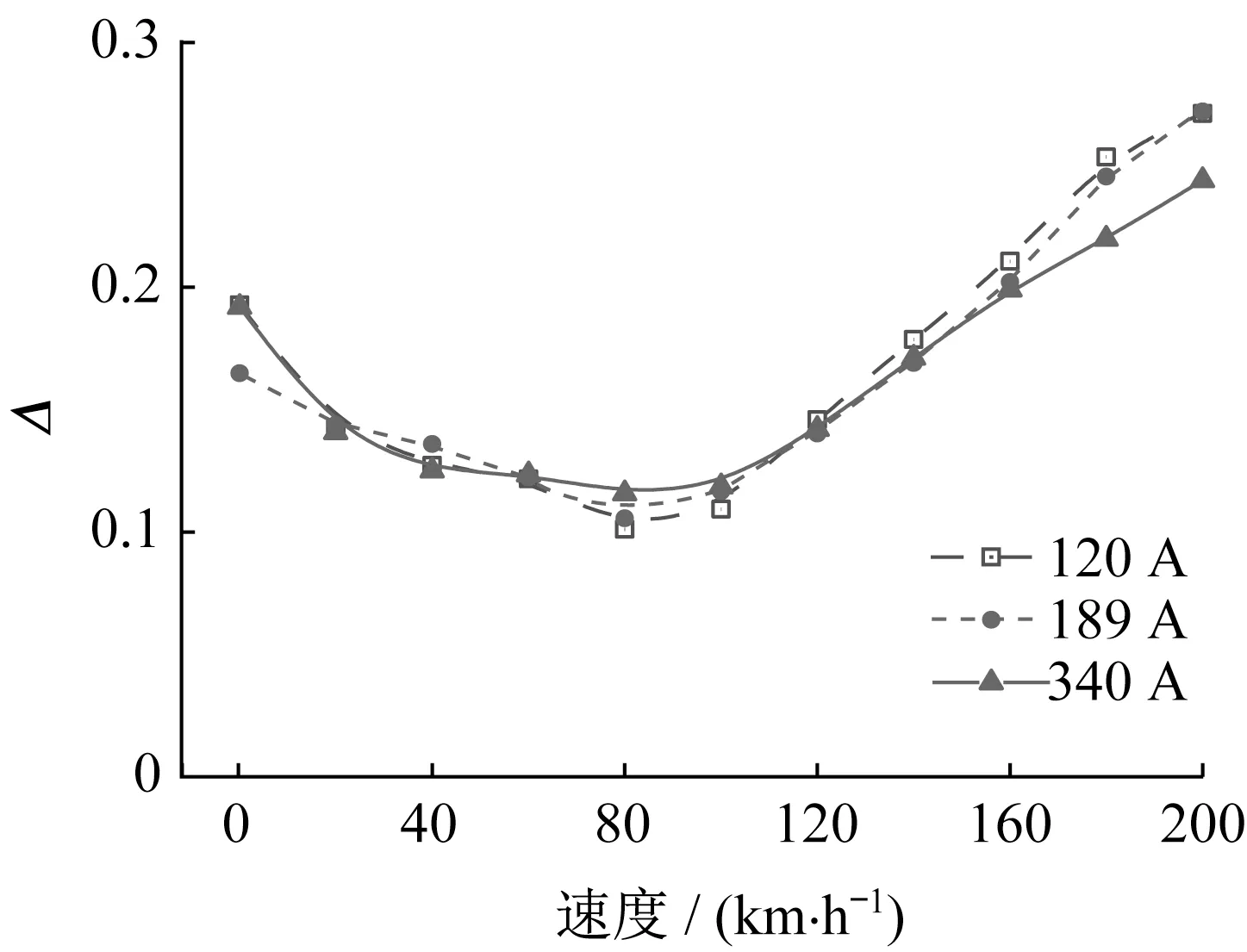
图12 Δ随速度变化Fig.12 Variation ofΔwith speed

综上可知，当列车低速运行时，纵向动态端部效应产生的气隙磁场端部效应波衰减快、影响范围小，半填充槽LIM和全填充槽LIM的气隙磁场基本一致，牵引力下降的原因主要是由缺少首尾部各一个节距内的绕组引起的；当列车高速运行时，牵引力下降大的原因是半填充槽LIM受纵向动态端部效应影响相比全填充槽LIM更大。由此说明，中低速磁浮列车采用端部半填充槽LIM在高速情况下电机牵引力衰减更大。

4 结语

以中低速磁浮列车用LIM为原型，建立一维气隙磁场数学模型，从气隙磁场角度分析了运行速度与端部效应的关系。LIM的纵向动态端部效应随着速度增加对电机影响增大，气隙磁场受端部效应影响畸变愈加剧烈，使得电机出端区域、入端区域的涡流阻力急剧上升，电机的牵引力随速度的增加而下降，电机效率下降。结合半填充槽LIM参数建立了有限元仿真模型，分析了速度与LIM的气隙磁场、牵引力和次级感应板涡流的关系，验证了理论模型的科学性，并对比了2种填充槽LIM牵引力下降情况，发现半填充槽结构在高速下电机牵引力衰减更为显著。