物理矛盾与四大分离原理
2022-01-15颜惠庚
颜惠庚 李 弘
(常州市技术创新方法研究会,江苏 常州 213031)
矛盾理论是TRIZ 九大经典理论之一。TRIZ 创始人阿奇舒勒认为:“每个伟大发明的结果就是解决一个或多个矛盾”。因此,从某种意义上来讲,技术创新的本质就是发现并解决技术系统中存在的矛盾。
前两讲中已经介绍过,阿奇舒勒将技术系统中的矛盾分为技术矛盾和物理矛盾两大类。在技术系统中,两个不同参数之间产生的矛盾叫技术矛盾,同一个参数有不同的要求而产生的矛盾叫物理矛盾。之所以这样分类,是因为解决这两类矛盾的途径和方法有所不同。
本讲将着重讨论物理矛盾的解决方法。
1 常见的物理矛盾
在国防、日常生活和工农业生产活动中,物理矛盾几乎无处不在。例如:侦察机应飞行得很快,以便尽快离开被侦察的地区,但在被侦察的地区上空又应飞行得很慢,以便多收集资料。
飞机的机翼应有大的面积以便起飞与降落,但又要较小以便高速飞行。
飞机发动机罩既应该加大直径,以便吸入更多的空气,但又应该减小直径,以增加该罩与地面的距离。
汽车应该尽量减少自重,这样既能减少油耗又能提高速度,但是这样做,汽车自身的安全性能又会降低。
钓鱼杆应该足够长,以满足使用要求,但最好也要足够短,以方便携带。
咖啡应尽可能热,以保持其味道,但又不能太热,以防止烫伤饮用者。
钢笔的笔尖应该细,以使钢笔能够写出较细的文字,同时钢笔的笔尖又应该粗,以避免锋利的笔尖将纸划破。
根据物理学中常用的参数,物理矛盾又可以从几何类、材料及能量类、功能类三个角度进行表述,如表1 所示。

表1 常见物理矛盾的具体参数
2 物理矛盾的解决途径
相对技术矛盾而言,物理矛盾是一种更为尖锐、更为本质的矛盾。如图1 所示,解决物理矛盾的核心思想是实现矛盾双方的分离。TRIZ 理论在总结解决物理矛盾的各种研究方法的基础上,提出了四大分离原理,即空间分离、时间分离、条件分离、整体与部分分离。
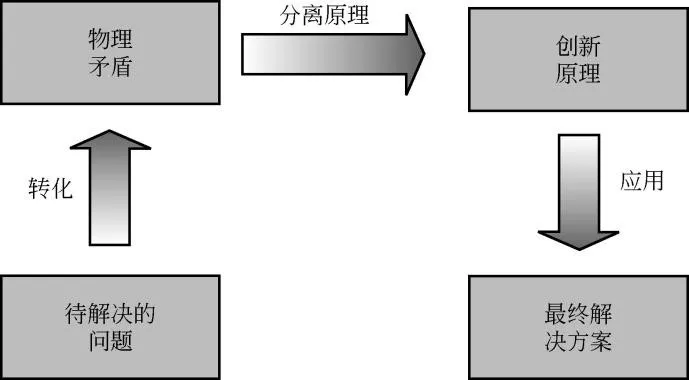
图1 物理矛盾的解题模式与流程
分离原理是TRIZ 针对物理矛盾的解决而提出的,其核心思想就是将矛盾双方进行分离,分别构成不同的技术系统,以系统与系统之间的联系代替内部联系,将内部矛盾外部化。
当分离原理确定后,还是必须借助40 个发明原理来为我们提供解决问题的思路,表2 列出了四大分离原理与40 个发明的关系。

表2 分离原理与发明原理关系
3 应用分离原理解决物理矛盾
3.1 空间分离原理
空间分离的应用条件:系统的某个参数出现相反(或不同)的要求,但又并不出现在同一个空间。这时,可以将矛盾双方在不同的空间上分离开来,以获得问题的解决或降低问题的解决难度。
案例5-1:玻璃杯。
玻璃杯中的水要热,以使茶叶的色香味得到充分展现,但又不能热,否则会导致手指烫伤,如图2 所示。

图2 玻璃杯
设问:何处要热——杯子内,何处要冷——杯子外。
判断:空间不重迭,符合空间分离的条件。
发明原理:03 局部质量原理 杯体加装隔热层
07 嵌套原理 真空保温杯
案例5-2:立交桥。
为防止交通事故的产生,就必须解决道路交通中车辆有序通行的问题,保证东西方向的道路和南北方向的道路都能畅通无阻。
设问:何处需要通行——东西方向的道路,何处需要停止——南北方向的道路。
判断:空间不重迭,符合空间分离的条件。
发明原理:17 空间维数变化原理
根据这一原理,设计了立交桥,如图3 所示。类似的案例还有鸳鸯火锅、电冰箱、快餐盒等。

图3 立交桥
3.2 时间分离原理
时间分离的应用条件:系统的某个参数出现相反(或不同)的要求,但又并不是同时出现。这时,可以将矛盾双方在不同的时间上分离开来,以获得问题的解决或降低问题的解决难度。
案例5-3:折叠式自行车。
在骑自行车的时候,希望自行车体积要大,以便能够载人或者载物,但是在停放自行车的时候,又希望自行车体积要小,以便节省停车场的空间。
设问:何时要大——骑行时,何时要小——停放时。
判断:时间不重叠,符合时间分离的条件。
发明原理:01 分割原理
根据这一原理,折叠式自行车解决了这一物理矛盾,在使用的时候展开自行车,在停放或携带的时候,折叠起来,如图4 所示。

图4 折叠式自行车
案例5-4:狂风超音速战斗机。
对于飞机的机翼而言,为了具有更好的承载能力,以提高更大的升力,我们希望它大一些,但是为了在航空母舰有限的面积上多放飞机,我们又希望它小一些。矛盾集中在几何尺寸的既想大又想小的物理矛盾上。
设问:何时要大——飞行时,何时要小——停放时。
判断:时间不重叠,符合时间分离的条件。
发明原理:01 分割原理
采用折叠式机翼可以实现机翼面积的时间分离,用以解决这一物理矛盾。飞行的时候展开机翼,停放的时候让机翼折起来,如图5 所示。

图5 狂风超音速战斗机
该飞机能够得到平直翼和三角翼的优良飞行特性,极大地节约了在起飞、降落过程和高速飞行过程中的能量消耗。
案例5-5:交通信号灯(红绿灯)。
城市交叉路口为防止交通事故的产生,就必须解决道路交通中车辆有序通行的问题,保证东西方向的车辆和南北方向的车辆都能有序通行。
设问:何时可以通行——其他车辆停止时,何时需要停止——其他车辆通行时。
判断:时间不重迭,符合时间分离的条件。
发明原理:19 周期性作用原理
根据这一原理,设计采用红绿灯,如图6 所示。

图6 红绿灯
类似的案例还有:钓鱼杆、露营帐篷、折叠伞等。
3.3 条件分离原理
条件分离的应用条件:系统的某个参数出现相反(或不同)的要求,而且时间和空间有交叉但无法使用时间分离或空间分离来解决物理矛盾时,应该考虑采用条件分离的手段。
条件分离是将矛盾双方在不同的条件下分离开来,以获得问题的解决或降低问题的解决难度。
案例5-6:跳水池。
跳水池里的水要软,以减轻水对运动员的冲击伤害,但又要求水必须硬,以支撑运动员的身体,水的软硬取决于跳水者的入水速度。
设问:什么情况下需要硬——入水时,什么情况下需要软——入水时。
判断:由于时间和空间都重迭,不符合时间、空间分离的条件,所以考虑采用条件分离原理。
发明原理:03 局部质量原理
35 物理或化学参数改变原理
解决的方法是采用局部充满气泡的跳水池,以解决这一物理矛盾,实现条件上的分离,如图7 所示。

图7 跳水池
案例5-7:交通环岛。
城市交叉路口采用红绿灯,固然可以解决交通安全的问题,但这是在牺牲一定的通行效率的前提下获得的,是否可以采用别的更高效的办法?
设问:什么情况下需要通行——同一地点的任何时间,什么情况下不能通行——同一地点的任何时间。
判断:由于时间和空间都重迭,不符合时间、空间分离的条件,所以考虑采用条件分离原理。
发明原理:14 曲面化原理
根据这一原理,人为设置所有车辆必须逆时针方向进入环岛和条件,从“面”实现了车辆的分离,如图8 所示。

图8 交通环岛
类似的案例还有:汽车安全带、混合液体的蒸馏(或分馏)、高速公路超速监测、不合格产品的检测等。
3.4 整体与部分分离原理(也称系统级别分离)
所谓整体与部分分离原理,是将矛盾双方在不同的层次分离,以解决问题或降低解决问题的难度。当矛盾双方在关键子系统的层次只出现一方,且该方在子系统、系统或超系统层次内不出现时,可以进行整体与部分分离。
案例5-8:轮船与声呐探测器的分离。
在利用轮船进行海底测量工作时,早期是把声呐探测器安装在轮船上的某个部位,这样在实际测量时,轮船本身就会成为干扰源影响到测量的精度和准确性。
当物理矛盾无法用时间、空间、条件达到分离目的时,应当考虑采用整体与部分分离原理。对应问题:需要及不需要状况下,是否可以将系统与子系统分开?
设问:需要声纳作为海底测量的部件,但轮船本身并不需要此部件,则部件与轮船可以分离吗?
判断:可以分离。
发明原理:02 抽取原理
一种解决方法是轮船利用电缆拖着声呐探测器,以在黑暗的海洋中感知外部世界的信息,如图9 所示。因此,被拖拽的声呐探测器与产生噪声的轮船之间在空间上就处于分离状态,互不影响,实现了矛盾双方的分离。

图9 声呐探测器
案例5-9:交通枢纽大型立交桥。
在交通流量巨大的交通枢纽地区,要保证车辆不积压、不造成交通阻塞,就必须将各方向的车辆进行分流。
设问:道路上的车辆总是需要转向、掉头,但并不是所有车辆都在同一地点、同一时间需要转向、掉头,可以分离吗?
判断:可以分离。
发明原理:02 抽取原理
12 等势原理
17 空间维数变化原理
在大型立交桥的设计中,可以把各个方向上所有的转向、掉头都从主干道上作为子系统分离出去,如图10 所示。

图10 大型立交桥
类似的案例还有:空中加油机、分体式空调机、电脑移动硬盘(U 盘)、电脑鼠标等。
通过以上四大分离原理及其案例的介绍,我们可以知道解决物理矛盾的基本逻辑是:首先要确认问题是否属于物理矛盾(同一个工程参数出现相反或不同的要求),其次判断适用哪种分离原理,然后选择适当的发明原理进行思考,最后形成概念解。
4 其他案例
接下来,将通过案例5-10,进一步介绍如何应用分离原理解决实际问题。
案例5-10:打桩问题。
在把混凝土桩打入地基的过程中,人们希望桩头比较锋利,以便使桩容易进入地面,同时又不希望桩头过于锋利。因为,在桩到达指定的位置后,过于锋利的桩头,不利于桩承受较重的负荷而保持稳定。
应用空间分离原理解决混凝土打桩的问题,如图11 所示。在桩的上部附加一个锥形的圆环,并将该圆环与桩牢牢地固定在一起,从空间上将矛盾进行分离。这样一来,既保证了混凝土桩容易打入地基,同时又可以使混凝土桩能够承受较大的载荷。
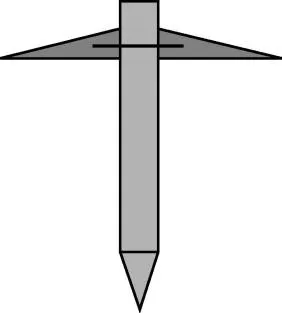
图11 应用空间分离原理解决打桩问题
应用时间分离原理解决混凝土打桩的问题,如图12 所示。在混凝土桩的导入阶段,采用锋利的桩头将桩打入地面,当桩到达指定的位置后,将桩头分成两半或者采用内置的爆炸物破坏桩头,使得桩头有较大的面积而可以承受较大的载荷。

图12 应用时间分离原理解决打桩问题
应用条件分离原理解决混凝土打桩的问题,如图13 所示。在桩身上增加一些螺纹结构,当把桩旋转起来时,桩就向下运动;如果桩不旋转,桩就保持静止,从而解决了方便导入桩与桩承受较大载荷之间的矛盾。

图13 应用条件分离原理解决打桩问题
应用整体与部分分离原理解决了混凝土打桩的问题,如图14 所示。将原来一根较粗的桩,用一组较细的桩来代替,从而方便地解决了导入桩与桩承受较重载荷之间的矛盾。

图14 应用整体与部分分离原理解决打桩问题
5 技术矛盾转换为物理矛盾
技术矛盾是技术系统中两个参数之间存在的相互制约,物理矛盾是技术系统中一个参数无法满足系统内相互排斥的需求。然而,无论是物理矛盾还是技术矛盾,都反映的是技术系统的参数属性。因此,它们之间又是相互联系的。
例如:为了提高技术系统中一个参数A 的效率,需要对系统中这个参数A 进行加热,但是加热会导致技术系统中另一个参数B 由于温度太高而降低功能,因此这是一对技术矛盾。同样,这样的问题还可以用物理矛盾描述为既希望温度高又希望温度低。温度高可以提高A 的效率,但是恶化了B 的功能;而温度低又无法提高A 的效率,但是也不会恶化B 的功能。因此,技术矛盾和物理矛盾之间是可以相互转化的。
因此,在作为技术矛盾出现的问题没办法解决时,可以转化为物理矛盾,也许这样能解决问题。接下来将通过案例5-11 来介绍如何将技术矛盾转换为物理矛盾。
案例5-11:安瓿瓶的密封问题。
制药企业生产液体针剂较多采用如图15 所示的安瓿瓶作为定制包装,当药液装入安瓿瓶后,需要通过高温迅速将安瓿瓶进行封口。

图15 安瓿瓶
这里产生的矛盾表现为一个典型的技术矛盾,即:我们希望通过较高的温度使安瓿瓶口快速熔融密封(优化参数A:生产率),但高温产生的热量会通过瓶体传导给药液,对药物产生有害影响(恶化参数B:物体产生的有害因素)。
现在需要寻找一个控制参数C,并要求参数C 必须要高,同时参数C 还要低;或者参数C 必须存在,而且参数C 不能存在,如图16 所示。

图16 寻找控制参数C
将该问题转变成为物理矛盾,选温度作为控制参数C。物理矛盾可描述为:温度C 增加,生产率A 提高,产生的有害因素B 增加;反之,生产率A 降低,有害因素B 减少;温度既应该高,以提高生产率;又应该低,以减少有害因素的产生。
至此,我们就将一个技术矛盾完全转化成了一个物理矛盾。至于如何解决这个物理矛盾,当然是用四大分离原理、再用发明原理来提供解决思路。
