断面形状对虹吸式出水流道水力特性的影响

2022-01-15陈曜辉冯建刚钱尚拓佟宏伟

水利水电科技进展 2022年1期

陈曜辉，徐辉,，冯建刚，钱尚拓，佟宏伟

(1.河海大学水利水电学院，江苏南京 210098； 2.河海大学农业科学与工程学院，江苏南京 210098；3.西藏农牧学院水利土木工程学院，西藏林芝 860000; 4.上海城投水务工程项目管理有限公司，上海 201103)

泵站虹吸式出水流道由于停机断流方便，在泵站工程中有着广泛的应用。由上升段、驼峰弯管段及下降段组成，其中上升段连接水泵出口的过渡弯管段，下降段连接出水池。当水泵起动后，水泵抽排的水体首先填充流道上升段的空间，水面逐渐上升，然后翻过驼峰向下降段溢流，在此过程中原本占据流道的空气，受流道内涌入水体的驱动排出。下降段形成水气混合出流，管道内的空气在水流的挟带下逐渐排出，最终在管道内形成满管稳定虹吸。从机组启动到管内空气排尽的整个过程称为虹吸形成过程。可以按照排气方式不同，将该过程划分为三个阶段：水力驱气、水力挟气和虹吸稳定流[1-2]。虹吸形成过程中，管壁压力和水泵扬程等随着时间的变化亦发生复杂的变化，不少实测资料都反映该时段的扬程、管壁压力值较稳定后的正常工作扬程、压力值大得多。若虹吸形成时间过长甚至最终未能形成满管流，或者虹吸形成过程中水力损失过大，则会造成扬程偏高、机组震动等危害，影响泵站的安全、高效运行[1]。

对于虹吸式出水流道的研究国内外学者已做了较多的工作。Babaeyan-Koopaei等[3]对虹吸式溢洪道开展了水工模型试验以分析其水力性能，发现驼峰段的滞留气囊会降低虹吸管的排泄流量。王晓升等[4]采用欧拉多相流模型与RNGk-ε湍流模型对某泵站虹吸式出水管虹吸过程中的气液两相流进行了数值模拟，并分析虹吸形成过程中的压力变化规律。徐磊等[5]比较了某大型低扬程泵站不同湍流模型的定常数值计算结果，认为二方程湍流模型在虹吸式出水流道计算上具有优越性。王芃也等[6]使用CFX软件进行了包含水泵的泵站装置模型全模拟，着重分析了虹吸式出水流道内部流态、水头损失、以及不同截面的涡量。雷瑶等[7]运用VOF模型及RNGk-ε模型模拟了卫生洁具内的气液两相流动，分析了管道内部结构对虹吸性能的影响。李琳等[8]采用FLUENT软件中VOF方法的标准k-ε模型和对虹吸式输水管中的虹吸流动过程进行了数值模拟，得到其过流能力、速度场、压降随水头的变化规律。冯建刚等[9]采用RNGk-ε模型模拟了某泵站虹吸式出水管，研究了虹吸形成时间特性及其改善措施。谭淋露等[10]利用RNGk-ε模型对虹吸式出水管进行了数值模拟，分析其内部水力特性，并通过改变主要参数进行了水力优化。张雪[11]采用标准k-ε模型对虹吸式出水流道进行了数值模拟，对虹吸式出水流道进行了优化设计。李秀萍[12]采用RNGk-ε模型对虹吸式出水流道进行了数值模拟研究，分析了导叶出口剩余环量对流道水力性能的影响以及关键流道参数对泵装置扬程和效率的影响。

综上所述，RNGk-ε湍流模型能够很好地模拟虹吸式出水流道的虹吸形成过程。研究者们常应用VOF方法模拟虹吸式出水流道内部水气两相流，但很少考虑气体的可压缩性，基本认为气体不可压缩且密度为常数，而虹吸过程中管内压力变化极大，气体的可压缩性不可忽略[13-14]。此外，研究者们关注的重点多是虹吸式流道内部气液两相流的模拟以及泵站虹吸式出水流道的参数结构对其水力特性的影响及其优化设计等，例如上升角、下降角、驼峰段面高宽比等，关于断面形状变化对虹吸式出水流道内部流动变化的影响鲜有研究。本文采用VOF方法结合RNGk-ε湍流模型对虹吸式出水流道进行模拟，分析不同断面形状对虹吸式出水流道水力特性的影响。

1 模型构建

1.1 虹吸式出水流道概况

研究对象的原型为上海市某取水泵站虹吸式出水流道，由过渡弯管段、上升段、驼峰段、下降段及出水池5个部分组成，其中，过渡段进口为与水泵出口连接的圆形断面，流道进口到驼峰段前均是圆变方的过渡变化，驼峰段各断面为稍扁平的矩形断面，驼峰段出口到出水池断面均为矩形，宽度不变、高度渐扩，具体结构布置如图1所示。其中，虹吸式出水流道进口直径D=200 mm，进口弯管包角α1=58°，上升角α=34°，驼峰段包角α2=67°，驼峰段高度H=114 mm，驼峰段宽度B=380 mm，下降角β=37°，进口至驼峰顶水平长度L1=661 mm，驼峰顶至出口水平长度L2=817 mm。图2为计算区域三维模型图。

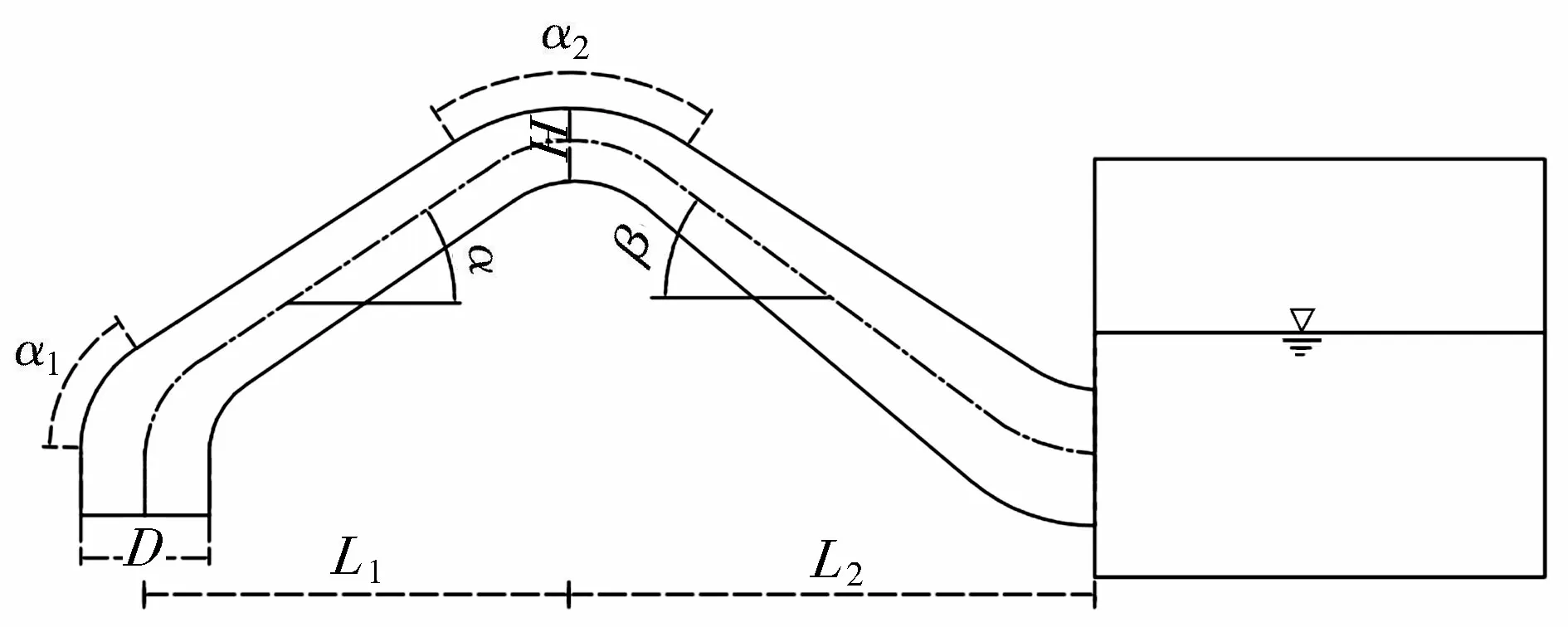
图1 虹吸式出水流道示意图

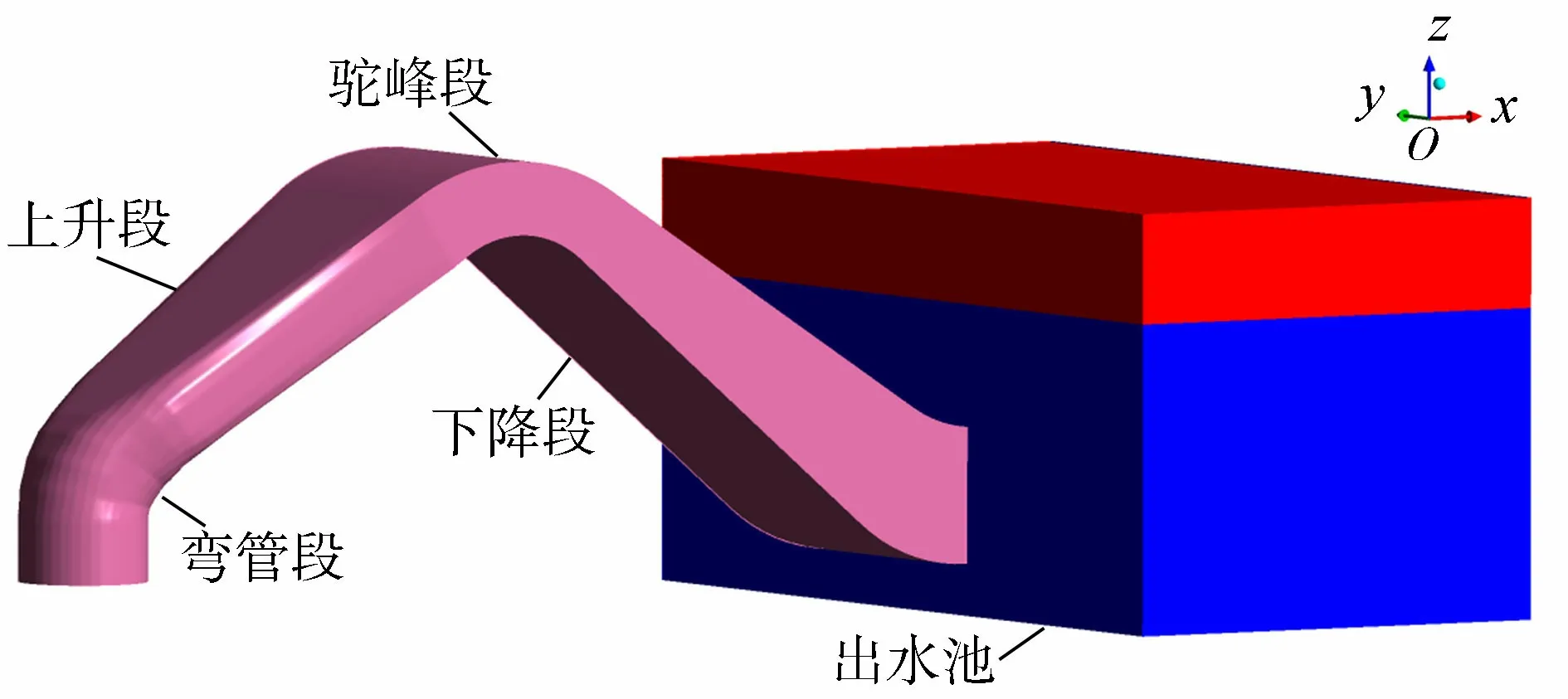
图2 虹吸式出水流道三维模型

断面变化的渐变体型虹吸式出水流道被广泛应用于工程量较大的大流量低扬程水泵机组，但施工难度相对增大。城市排水泵站使用的流道断面变化相对简单，沿程断面变化不大，便于施工。本文以渐变断面虹吸式出水流道为基础，在保证管道进口面积、沿流道中心线不变的前提下，将渐变断面流道简化为理想化的等截面圆形和方形断面流道，即沿程各个断面形状均与进口断面相同的圆管和方管，以此来对比不同断面形状对流道水力特性的影响，图3为等截面圆管和方管的虹吸式出水流道三维模型。

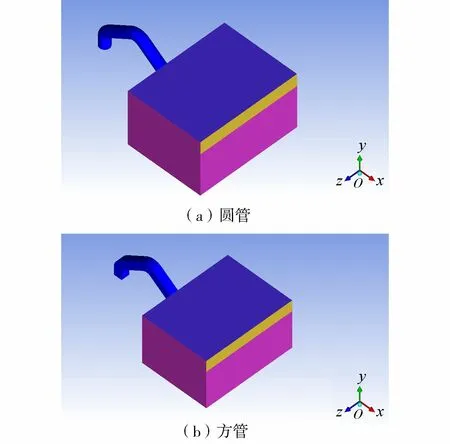
图3 等截面的虹吸式出水流道三维模型

1.2 控制方程与湍流模型

虹吸式出水流道的虹吸形成过程是复杂的气液两相流，基本流动控制方程如下：

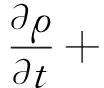
(1)

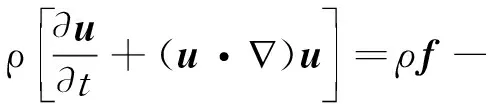
(2)

式中：ρ为流体密度；u为流体速度；t为物理时间；p为流体微单元所受压力；f为质量力；μ为动力黏度系数。

对于理想气体，考虑其可压缩性，其密度表达式可以写为

(3)

描述多相流混合的k-ε控制方程为

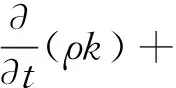
(4)

(5)

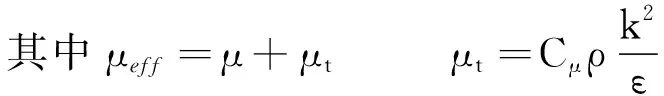
Gk=μt[∇u+(∇u)T]∇u

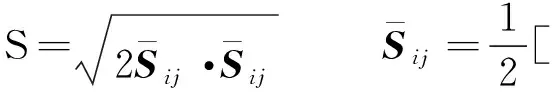
式中：k为湍动能；ε为耗散率；μeff为有效混合黏度；μt为涡黏系数；Gk为由于黏性力导致的湍动能产生项；S为平均应变率张量系数；常数项Cμ=0.084 5，C1ε=1.42，C2ε=1.68，σk=σε=0.75，η0=4.38。

采用VOF方法对含有自由液面的虹吸式出水流道进行气液两相流模拟。分别定义αw和αa为计算流道内水和气体所占的体积分数，则气体的体积分数可以用下式表示：

αa=1-αw

(6)

αw=0表明该网格内全是空气，0<αw<1表明该网格内既有液体也有空气，即存在自由液面，此时网格内水气混合物的密度和黏度分别为

ρ=αwρw+(1-αw)ρa

(7)

μ=αwμw+(1-αw)μa

(8)

1.3 计算网格与边界条件

网格质量直接影响数值模拟的精度与收敛速度，本文使用六面体结构化网格对计算区域进行划分。此外由于流道截面整体从圆形渐变至方形，还采用O形网格剖分方式对计算域作结构化网格处理。对于含有自由液面的出水池，在水面附近处的网格进行了加密处理。图4所示为虹吸式出水流道网格划分示意图。本文对已划分的计算域网格运用理查德森(Richardson)外推法进行网格精度验证，经对比5套粗细不同网格方案，最后确定网格单元数为1 363 996个。近壁面y+最大为166.603，最小5.21，均值55.11。

图4 虹吸式出水流道网格划分示意图

图5为虹吸式出水流道设置的定解条件。进口设为流量入口条件，参照设计流量工况，入口流量范围设置为30～50 L/s。出水池底部及四周均是墙体，顶部与大气联通，其中与流道出口断面正对的墙稍矮于剩余的墙，矮的部分为水气共同压力出口。图中阴影部分为水体初始位置，留空部分为初始气体，即出水池水位以上及上升段部分为空气。值得一提的是本文设置的气相为理想气体，虹吸形成过程是一个有压的气液两相流，在此过程中气体会经历压缩、膨胀、分离与再聚合的复杂过程。将不可压缩气体与理想气体的虹吸形成时间、系统内部压力脉动和气液两相流流态的模拟值分别与试验结果比较，发现不可压缩气体较理想气体的模拟结果差，故对于虹吸式出水流道的模拟采用理想可压缩气体。

图5 虹吸式出水流道计算定解条件

2 计算结果与分析

2.1 数值模拟试验验证

虹吸形成过程分为水力驱气，水力挟气和虹吸形成3个阶段[1]。本文选择对比分析不同体型虹吸式出水流道虹吸形成以后的流动特性。水力驱气阶段和水力挟气阶段系统内部流动随时间变化显著，很难找到不同体型流道内比较统一的水气形态进行对比。将数值模拟结果与物理模型试验结果从流态、系统压力脉动、虹吸形成时间3个方面进行对比如图6所示。从图6可以看出，数值模拟结果与物理模型试验结果较为吻合，数值计算模型可靠。数值模拟虹吸形成后的压力以及正常流量工况下的虹吸形成时间均较为准确。在较小流量情况下虹吸形成时间有些许出入，这可能是由于小流量情况下，紧贴下降段下壁面的下滑水流与水面交界处发生剧烈旋滚，产生的气泡存在明显的往复运动。即管内水流流速较低，挟气能力不足，气泡所获得的能量不足以排出管道，随着浮力作用返回交界处，再次获得水流的冲击能量，经过几次这样的往复运动，随着水流最终排出管道。而VOF方法模拟小流量情况下的这些小气泡运动有些不足，是VOF模型本身局限性导致。

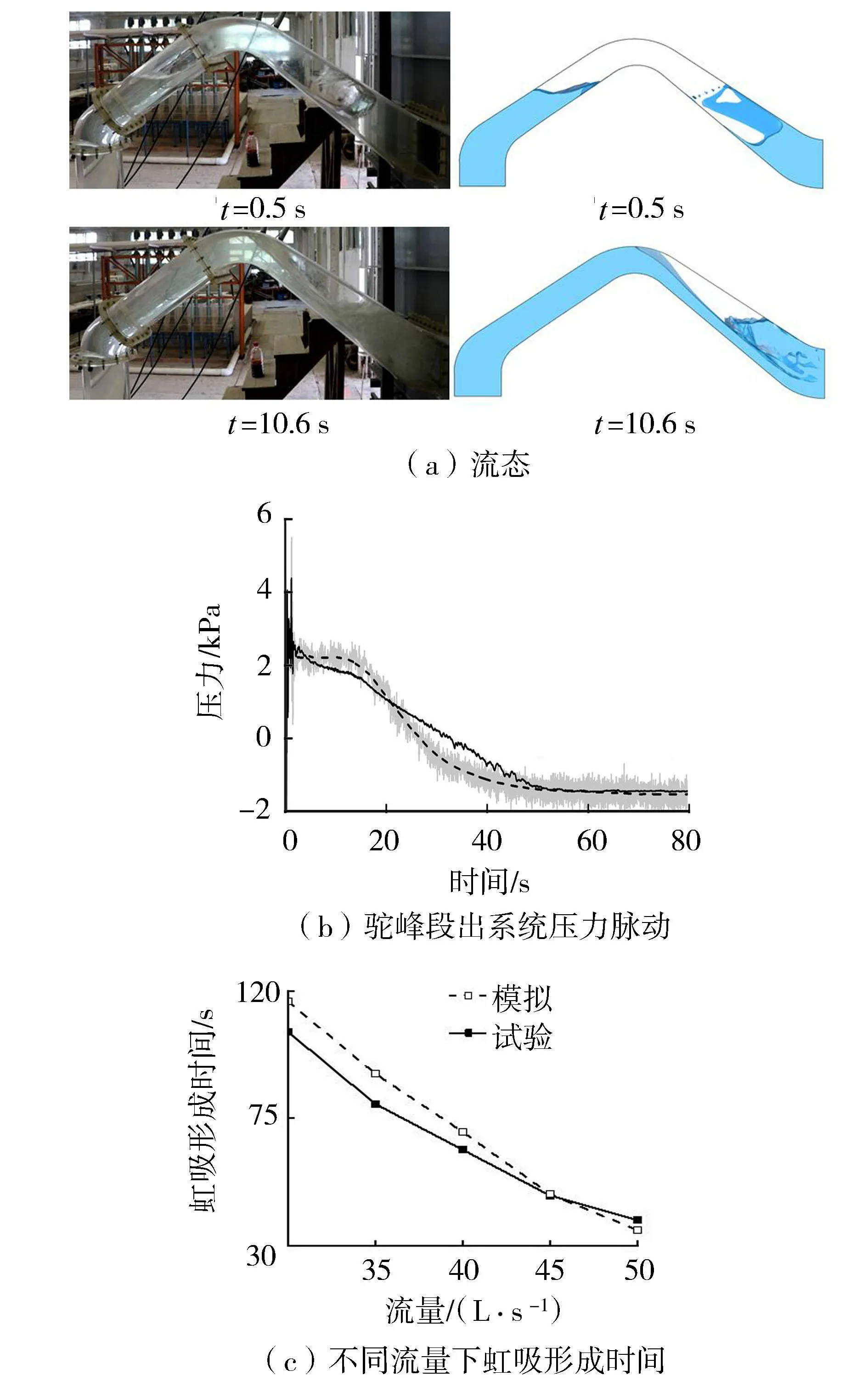
图6 数值模拟结果与模型试验结果对比

2.2 不同断面虹吸式出水流道流速分布规律

为了研究断面形状对虹吸式出水流道内部水流流动特性的影响，有必要分析各典型断面的流速分布情况。图7为虹吸式出水流道典型断面位置，分别为上升段起始断面(1—1)、驼峰段起始断面(2—2)、驼峰段中间断面(3—3)、下降段起始断面(4—4)以及出口断面(5—5)。

图7 虹吸式出水流道典型断面位置

对于3种形状断面而言，不同流量对各典型断面流速分布影响仅仅是数值差别而非规律性差别，故仅对比40 L/s流量工况下的流速分布情况。图8为3种形状断面各典型断面流速分布。从图8中可以看出：在上升段的流动中，即1—1断面和2—2断面，水流流速以轴向流速为主，流速均匀度稍有变差，这可能是由于上升段前过渡弯管段的影响。对比3种断面虹吸式出水流道，渐变断面的流道具有最佳的流速均匀度，整体流速分布较为均匀，而等截面圆形、方形断面流道主流偏下，圆管在上升段有小范围的低流速区出现，这说明过渡弯管段会使主流有一定的偏向，而类似渐变体型横向渐扩立面渐扁的断面有利于流动均匀。驼峰段2—2至4—4断面流速分布规律与上升段类似，驼峰弯管段的流速均匀度与进口处上升段有较大关系。对比下降段4—4至5—5断面中的流动可以看出，渐变断面虹吸式出水流道流速分布集中在中间偏上，两侧呈对称分布，等截面圆形、方形虹吸式出水流道流速从上到下呈由大到小分布。在设计简化等截面体型时，是保证其过渡段进口断面面积与渐变体型流道一致，而后续渐变断面体型流道在下降段在立面上渐扩，故其扩大的断面面积会产生对称分布的小流速区域。从流态上看，渐变断面的虹吸式出水流道出水更为均匀。

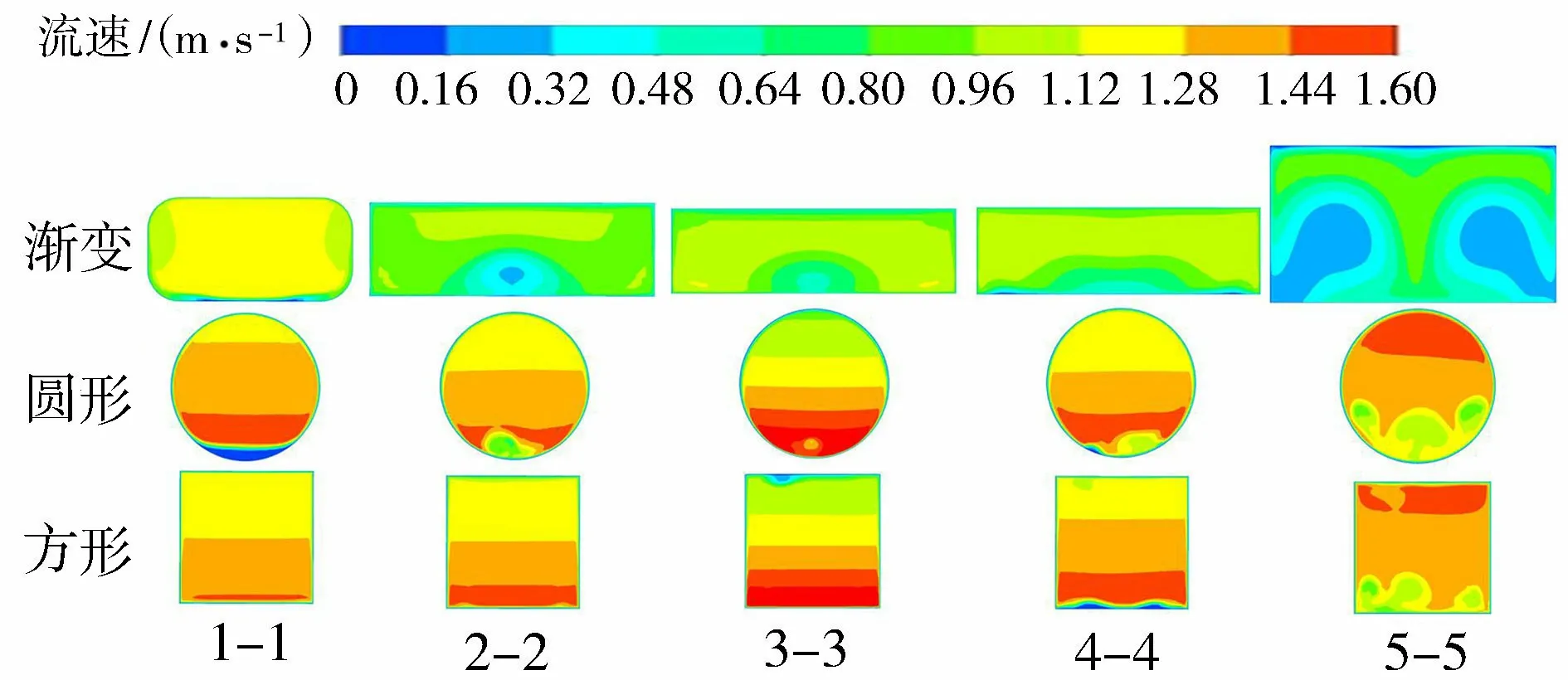
图8 典型断面流速分布情况

图9为不同断面虹吸式出水流道的中心剖面沿程流速分布，可以看出，在虹吸管上升阶段，水流经水泵出口与出水流道的过渡段进入虹吸式出水流道上升段之后，渐变断面流道和圆形断面流道上升段的低流速区较方形断面流道明显，这说明圆管进口过渡段比方管更容易出现低流速区，而实际水泵出口就是圆管，故设计过渡段的时候要充分考虑到这一因素。在驼峰弯管段，渐变断面流道水流轴向分布变得较为均匀，对比圆形断面流道来看，扁平的驼峰段有利于使上升段过来的水流变得更加均匀。进入下降段之后，由于驼峰段的作用，导致下降段的主流贴上壁。渐变断面的水流轴向速度分布更加均匀且明显小于另两种方案，这是由于其渐扩的下降段影响。等截面圆形与方形断面的水流在下降段的轴向速度分布呈现从上到下依次递减的趋势，且管道底部流速较低，可能出现脱流、旋涡等不良流态。

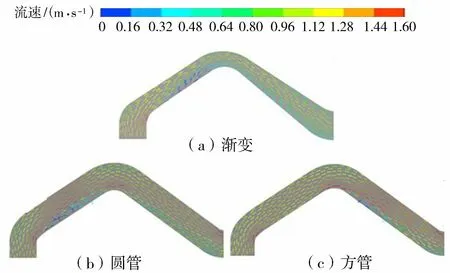
图9 不同断面虹吸式出水流道水流沿程流速分布

2.3 不同断面虹吸式出水流道水力损失

选用伯努利能量方程计算水力损失hw，选取虹吸管进口作为1断面，其出口作为2断面，水力损失计算公式如下：

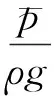
图10为不同断面虹吸式出水流道不同流量条件下的水力损失，可以看出水力损失随着流量的增加而增大。在所有流量工况下，渐变断面的水力损失最大，等截面方形断面的水力损失次之，等截面圆形断面的水力损失最小。这意味着管道断面形状对的水头损失影响很大，所以合理的设计有利于减小水头损失。渐变断面由于上升段断面经历圆变方的过渡，驼峰弯管段以及下降段至出口段又有截面的收缩和渐扩，这些都会使渐变体型的水力损失较大。另外，截面的变化越小虹吸式出水流道的水力损失会越小，但是某些截面设计不合理又会导致其内部虹吸形成过程中水流流态特性不佳，不利于机组安全运行。

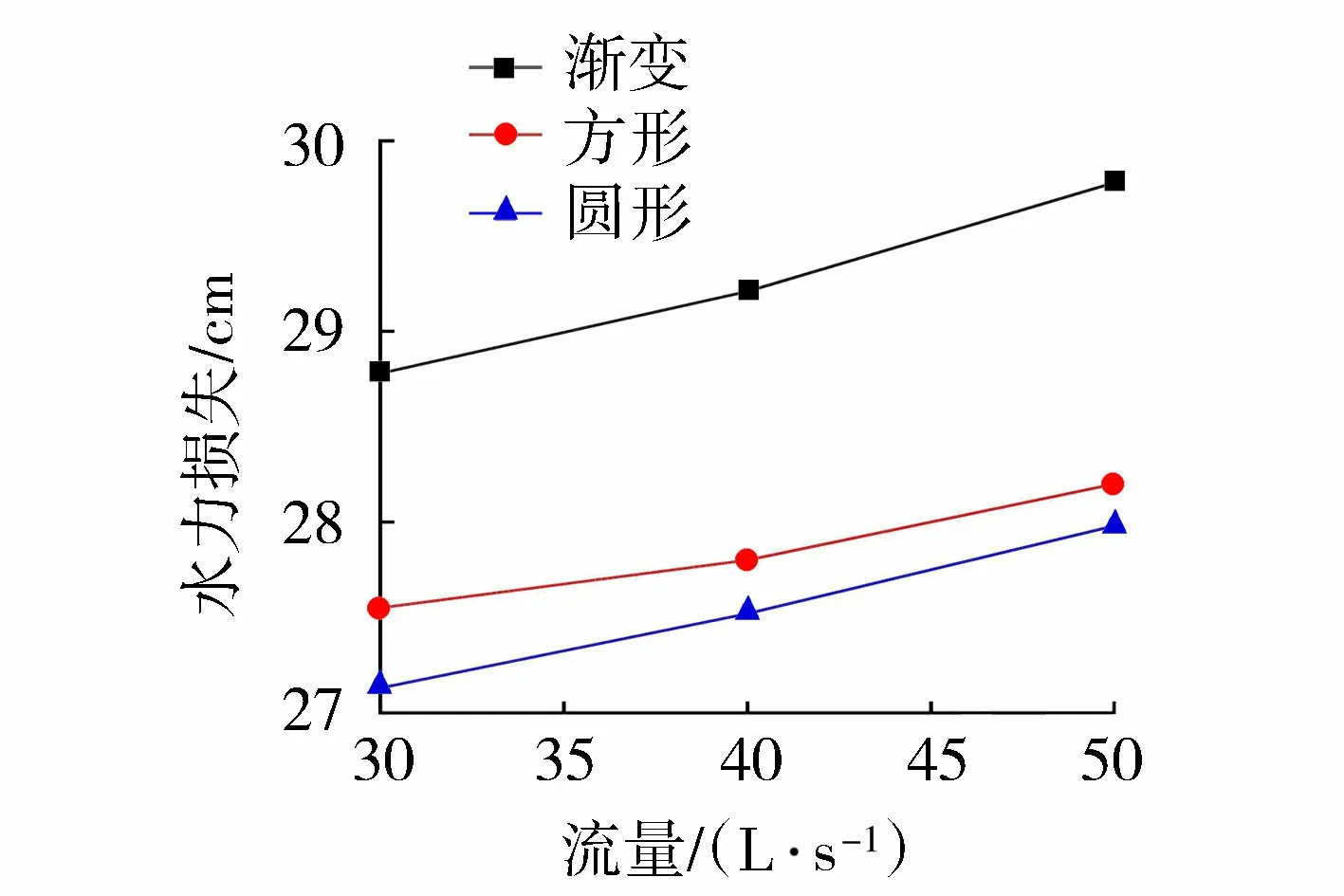
图10 不同断面虹吸式出水流道不同流量条件下的水力损失

2.4 断面形状对虹吸式出水流道虹吸形成时间的影响

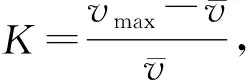
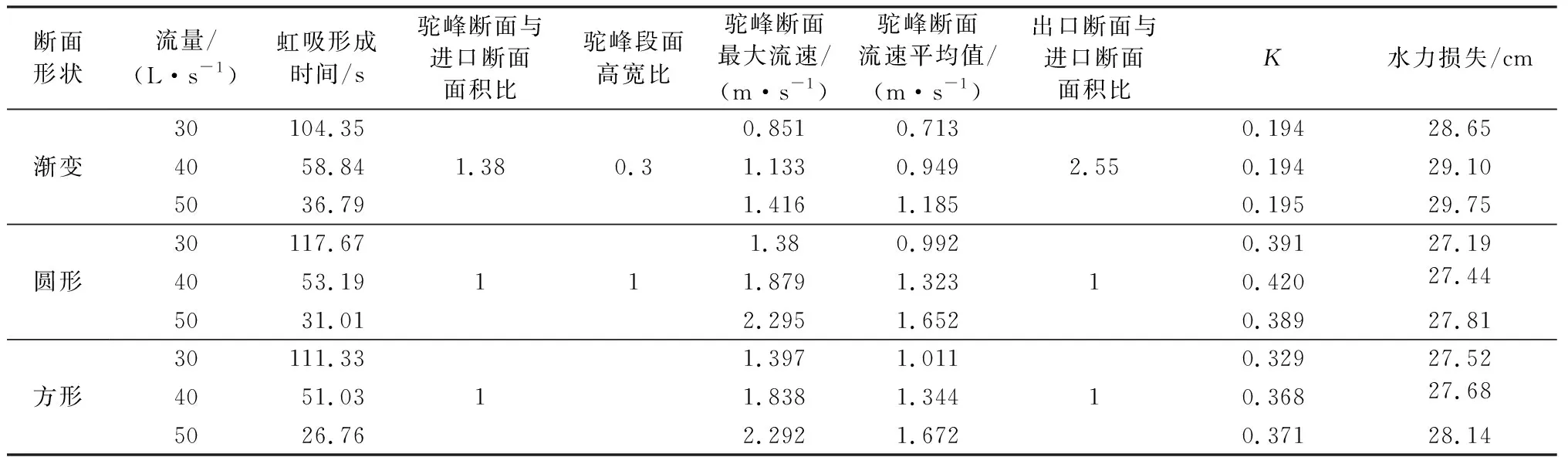
表1 不同断面虹吸式出水流道综合性能

从表1数据可以看出，从进口至出口，渐变断面截面形状从圆形逐渐过渡到扁平矩形且截面面积不断增大。但是渐阔的断面会导致其流道内部产生额外的水力损失。过流断面面积完全相同的圆、方管，断面形状不同，流道水力特性也存在显著差异。等截面圆管的虹吸形成时间比等截面方管要略长，这是因为断面形状导致的等截面圆管断面流速均匀度要比等截面方管断面差，但其水力损失相对略小一些。在小流量工况下，虽然渐变体型平均流速最小，但是虹吸形成时间最短，这说明了在某些小流量条件下流速分布均匀性对于虹吸完全形成具有相当大的作用。