基于水平集算法的污水中微生物图像分割研究

2022-01-15苗加庆李高平刘晓光

西南民族大学学报(自然科学版) 2021年6期

苗加庆，常兰，李高平，曾莉，刘晓光

(1.西南民族大学数学学院，四川成都 610041；2.成都理工大学工程技术学院科研处，四川乐山 610225)

近年来，随着人们生活水平的提高以及对水的需求量的增大，也促使污水处理技术的飞速发展，而污水处理的主要工艺之一就是活性污泥法工艺，其主要依据是污水中的有机污染物不断地被微生物吸附、分解，从而达到净化污水的目的，而这其中起着决定性的作用的就是微生物的情况，在处理过程中直接影响污水消化的效率的因素就是微生物的数量、种类，而本文的目的主要就是找出一种最佳的方法来实时了解、控制污泥中微生物的数量、种类及其生长阶段的情况.随着数字图像处理技术的飞速发展，其应用领域的许多研究成果也得以开发.论文主要采用水平集方法设计并实现了在活性污泥法中微生物图像的分割.比如在活性污泥净化系统中，通过水平集方法[1]分割出各时段的污泥中微生物图像，然后可以通过各阶段的微生物的数量、种类以及形态等来了解系统的处理性能.近几年研究者们在几何主动轮廓模型分割细菌图像投入了大量的研究工作，目前的主动轮廓模型可以大概根据其执行方法和表示方法的不同分为几何主动轮廓模型[2]和参数主动轮廓模型[3].特别的在拉格朗日构架中参数主动轮廓模型可以明确的表示为参数曲线.而在欧拉构架中几何主动轮廓模型则表示为二维方程的水平集[4].这些模型都是以水平集方法和曲线演化理论为基础的[1-2]，其主要思想就是采用确定的高维度方程的零水平集来表示曲线，通常称之为水平集方程，然后在偏微分方程(PDE)的基础上来演化这个水平集方程[4].主动轮廓模型具有许多优点，首先在演化中采用水平集方程表示的曲线可能会自然地合并或者中断[5]，以至于能够自动处理细菌图像拓扑结构的变化，而且水平集方程总是保持在一个固定的网格上，这样就可以使数值化方案更高效.论文针对活性污泥中常见的几种微生物，包括线虫、草履虫、累枝虫、轮虫和钟虫等微生物进行有效识别，如:在生的缘毛目多的情况下，说明污水处理效果良好，出水浊度和BOD5值低.如出现主要有柄纤毛虫，如盖虫、钟虫、轮虫、累枝虫、寡毛类时，则出水清澈透明，水质澄清良好.

1 活动轮廓模型的前期工作

1.1 CV模型简介

首先在Ω范围内定义一个演化曲线C，以其作为Ω的一个开子集ω的边界(也就是说ω⊂Ω且C＝∂ω)，在下文中，inside(C)表示区域ω，outside(C)表示区域

该方法是基于图像能量分割的最小化方法，以一个简单的例子来说明模型的基本思想[6]，假设图像μ0是由值为的两个近似分段常数强度的区域构成，进一步假设待检测的目标是由值区域表示，C0表示目标边界，则我们可以得到目标内部区域外部区域考虑如下“拟合”项:

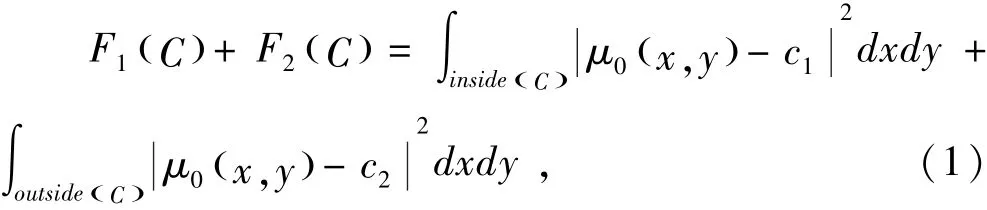
其中C为其它任何变量曲线，且常数c1，c2的值取决于曲线C，两个常数相应的是μ0的insideC和outsideC的均值，在这个简单的例子中，显然目标边界C0是拟合项的最小值.

这个是显而易见的，例如，如果曲线C是在目标的外部，那么就有F1(C)＞0且F2(C)≈0，而如果曲线C在目标的内部，那么就有F1(C)≈0而F2(C)＞0，如果曲线一部分在曲线内部一部分在外部，那么就是F1(C)＞0且F2(C)＞0，最终如果C＝C0那么拟合项就被最小化了，即曲线C恰好在目标的边界上.

能够注意到算法的关键不在于方程φ中采用的基于时间的PDE[7]，这与最小化问题得到的稳定性问题一样，可以由有限差分方法进行数值求解[8].

1.2 实验结果

将该模型应用于各种不同轮廓和形状的真实细菌图像，并得到了数值实验结果.同时给出了原始图像μ0的主动轮廓演化及其分段常数的近似值(就是c1和c2取平均).同时为了能够自动检测细菌图像的内部轮廓以及确保全局最小值的求解，采用Heaviside和Dirac delta方程(在ε＝h＝1条件下)的近似形式H2，ε和δ2，ε.其中只有其长度参数μ具有缩放功能.如果需要检测尽可能多的任何尺寸的边界，那么μ就应该取一个小值.如果需要检测大的目标(例如成块的目标)，那么此时μ就应该取一个较大的值.在实验中每次都会给出μ的确切的值以及初始水平集方程φ0.

在图1中，给出了C-V模型是如何分割带有不同形状和轮廓的细菌图像，而且其轮廓和形状都是自动检测的，不需要考虑第二个初始曲线.由于模型中采用了水平集，所以可以允许其自动改变图像的拓扑结构.并且该模型同样显示出模型可以成功检测不同强度且边界模糊的不同目标.同样图像的环面的内部轮廓是可以自动检测的，这都是因为其演化速度具有全局依赖性，同时曲线是自动向目标靠拢的.

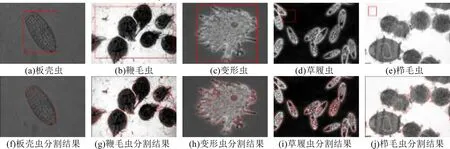
图1 CV模型分割结果Fig.1 Segmentation results of CV model

但是该模型依然存在许多的局限性，对于噪声较高的图像分割效果不太理想，而且分割结果存在较多的误分割的情况，而且有些细菌图像分割不完善，存在分割不足的情况.

1.3 实验结果分析

在本节介绍了基于Mumford-shah分割[11]技术以及水平集方法的主动轮廓模型.模型不依靠边缘方程来终止演化曲线目标边界.同样也不需要平滑初始图像，即使是对于带有强烈噪声的图像，这样图像边界的位置也是非常容易检测和保存的.通过该模型，可以检测出由图像梯度信息定义的边界的目标或者是边界非常平滑的目标，而这些都是传统的主动轮廓模型检测不出来的.

2 无需重新初始化的水平集演化

2.1 无需重新初始化模型介绍(LBF模型)

对于几何主动轮廓的一个变分公式，使得水平集方程的演化过程接近于一个符号距离函数，这样可以完全省去耗时的重新初始化步骤.这个变分公式包含一个内部能量项，其处罚了从符号距离方程接近水平集方程的偏差，还包含一个促使零水平集向目标图像特征运动的外部能量项.水平集方程的演化结果是呈梯度流的，结果使所有的能量方程最小化.本节的变分水平集方程相较于传统的水平集方程主要有三个优点.首先，其时间步长可用于解决偏微分方程，由此加速了曲线的演化[9].然后，水平集方程可由一般方程初始化，这样比采用符号距离方程创建更加高效而且实际运用更加简便.最后通过方程中的水平集演化可以由有限差分执行，而且其计算也更加高效.这个变分公式已经在医学图像和细菌图像应用中取得的不错的结果.尤其是在弱边界细菌图像上的应用.

在图像分割中，主动轮廓是向目标边界移动的动态曲线.为了达到这个目标，本文精确的定义了外部能量，其可以使零水平曲线移向图像的目标边界[10].令I为一幅图像，同时g为边缘指数方程定义如下:

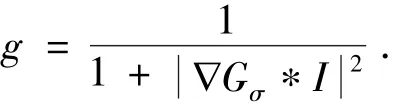
其中Gσ为标准偏差为σ的高斯核，定义方程φ(x，y)的外部能量如下:

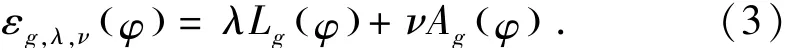
其中λ＞0且v为常数，同时Lg(φ)项和Ag(φ)定义如下:

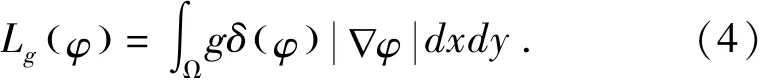
和

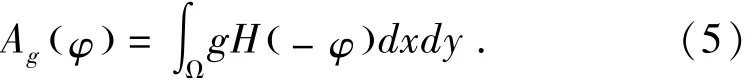
相对的，其中δ为一元脉冲函数，H为海维塞函数.定义总的能量方程如下:

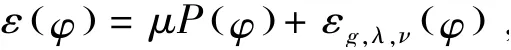
外部能量εg，λ，ν促使零水平集移向图像目标边界[12]，而内部能量项μP(φ)用于处罚演化中函数φ距符号距离方程的偏差.

为了使Lg(φ)量的几何意义更易理解，我们假设函数φ的零水平集可以由一个可微参数曲线C(P)来表示，其中P∈[0，1]，不难知道Lg(φ)能量方程计算函数φ的零水平集曲线的长度.(5)式中介绍的Ag(φ)能量方程是用于加速曲线演化.需要注意的是，当方程g为常数1时，(5)式中的能量函数应用于区域公式(5)中的能量泛函Ag(φ)可以视为的加权面积.能量泛函Ag的系数ν可为正也可为负，其主要取决于初始曲线与目标的相对距离.如果初始曲线在目标外面，系数ν在加权面积项中就应为取正值，这样轮廓就能快速缩小.如果初始曲线在目标的内部，系数ν就应取负值来加速轮廓扩张.通过变分法，函数ε的导数可以写为:

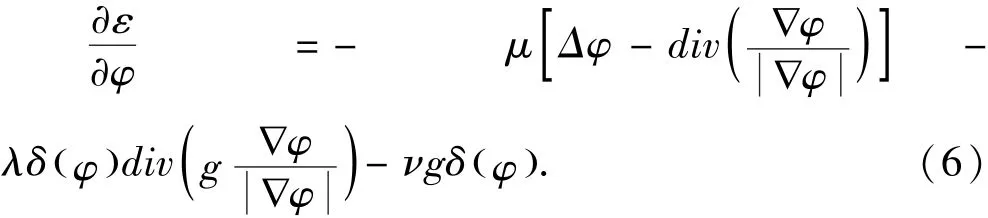
其中Δ为拉普拉斯算子，因此最小化了这个泛函数的方程φ就满足欧拉-拉格朗日等式∂ε/∂φ＝0.函数ε最小化的最速下降过程为如下梯度流[14]:

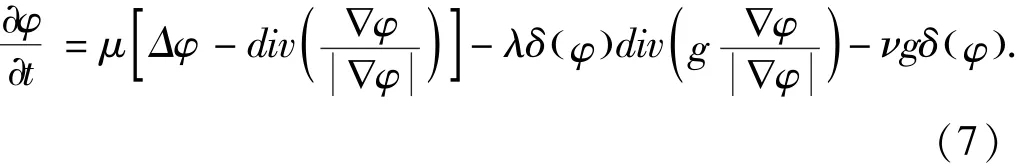
这个梯度流是该方法中水平集方程的演化方程.

在(6)式中的左边第二和第三项相当于对应能量泛函λLg(φ)和νAg(φ)的梯度流，其主要用于促使零水平曲线移向目标边界.而(7)式中的第一项与内部能量μP(φ)相关，其梯度流为中的为扩散率，如果则扩散率为正值且其影响为常规扩散，也就是说使函数φ

2.2 实验结果

变分水平集方法已经以不同的形式应用于各种真实细菌图像的分割问题，本节给出了所有的细菌图像分割实验结果.

图2给出了五幅细菌图像轮廓的演化结果，可以看到有些图像的两个细胞的部分边界是比较模糊的.用这几幅图像说明了该方法对弱边界图像分割仍具有很强的鲁棒性，从图2中可以看出，这个初始水平集的直线成功地演化为了目标边界，并且其形状也修复的很好.这个结果说明我们的方法对于提取图像弱边界具有良好的性能，而这也正是传统方法不能实现的.

图2 各种细菌的LBF水平集分割结果Fig.2 Segmentation results of the LBF level-set for various bacteria

但是该方法仍然存在容易被不相干信息干扰的缺点，这样就会出现误分割或分割不精确的现象发生，该算法对于初始水平集轮廓要求较高，不同的初始水平集分割结果相差较大，同时由于分割时对于分割区域的内部误分割情况较严重，因此需要进一步修正该算法.

2.3 实验结果分析

在本节中，提出了一种可以完全省略重新初始化步骤的变分水平集方程，相较于传统水平集方程，它可以通过简单的有限差分来进行分割且计算非常高效.采用了较大的时间步长来加速曲线的演化同时保持稳定，而且水平集方程不需要初始化为符号距离方程.这样不仅使计算比符号距离方程的计算更加高效，而且使其运用也更加灵活.该算法在细菌图像上的分割结果，尤其是在弱边界和强噪声图像分割中结果显示出较强的鲁棒性.

3 基于局部正弦拟合水平集图像分割

在本节中，采用正弦函数来表示传统主动轮廓模型的数据拟合量，并提出了一种适用于分割细菌图像的局部正弦拟合量主动轮廓模型.此外在模型中还引入了水平集正则项来避免由于演化水平集函数重新初始化引起的大量计算.实验结果表明当模型应用于分割不同类型的细菌图像时，其分割结果是精确且高效的.相较于Chan-Vese模型和局部拟合模型，本节的模型对于分割含有噪声的细菌图像是更加高效稳定.

3.1 介绍

在本节中，所有模型均采用正弦函数来表示图像的数据拟合量[15].受到LBF模型的启发，首先对局部拟合量做了一个简单的介绍，同时提出一个可以较好分割细菌图像的模型.然后将局部图像信息应用到模型中，从而可以分割出更多灰度不均匀的细菌图像.实验结果表明，该模型对不同类型的图像都可以达到较好的分割效果.而相比于C-V模型和LBF模型[9]，本节的模型分割结果更加精确高效.

3.2 拟建模型

在本节中，我们首先采用传统模型中广泛采用的正弦函数来表示数据拟合量，然后利用局部正弦拟合模型(LCF)进行细菌图像分割.

实际上，在真实图像中广泛存在灰度不均匀的问题，比如某些细菌图像.在本节中，局部图像信息和正弦拟合量结合起来，提出一个精确分割灰度不均匀的原始图像的LCF模型.令C为分隔图像区域Ω为两个区域的闭合曲线，其中两个区域分别为:Ω1表示(C)的外部区域、Ω2表示(C)的内部区域.对于一个已知点x∈Ω，定义局部拟合量如下[6]:

其中λ1和λ2为两个固定正常数，而Kσ为标准偏差为σ的高斯核函数.图像局部区域中心在定点X的灰度可以近似为内外区相应的两个值f1和f2，每个定点局部区域的大小可以由参数σ控制.

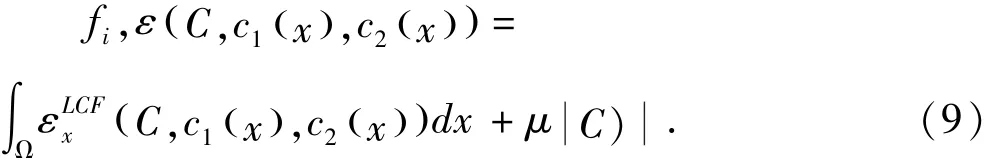
我们用水平集方程φ来表示曲线C，其中包含了水平集方程的正则项.则能量方程可以表示如下:

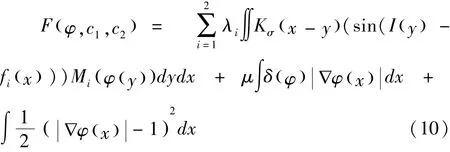
其中M1＝H(φ)且M2＝1-H(φ)，其中海瑟维方程H和δ-Dirac方程定义如下:

和

为了在迭代过程中保持精确的计算结果和稳定的水平集估算[17]，引入一个水平集正则项，其符合如下能量方程:

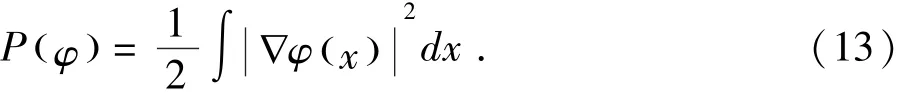
结合(10)式的能量方程和(13)式的正则项，则可以得到完整的能量方程如下:

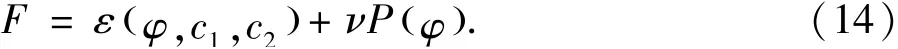
在实际应用当中，海瑟维方程和δ-Dirac方程可由相应的平滑方程Hε和δε近似得到，在本文中定义如下:

和

在实际计算当中，我们采用(15)式中的Hε来代替H.然后采用标准梯度下降法来最小化上述能量方程.一方面，固定φ不变，相对方程f1(x)和f2(x)来最小化能量方程[18]，则可以得到:

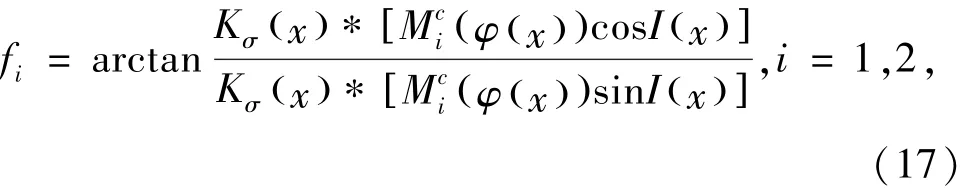
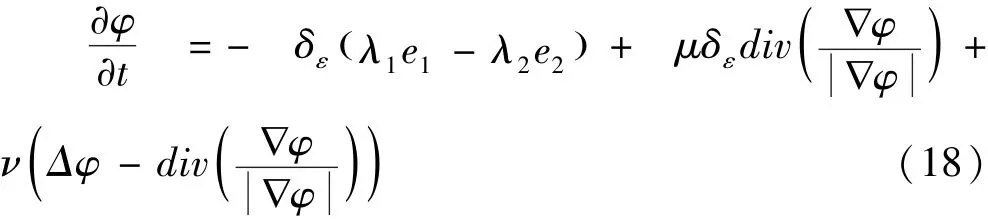
其中δε由(16)式中的给出[19]，且e1和e2定义如下:

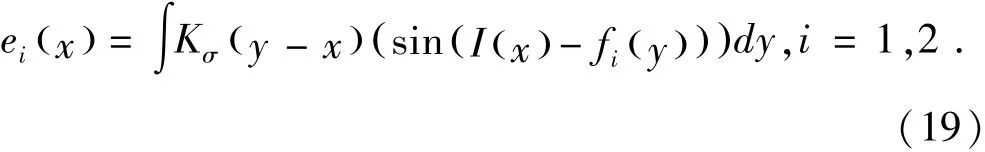
在(18)式中的水平演化中，第一项由局部正弦拟合量得到，其在分割灰度不均匀图像中占主导作用.后两项是正则项，相应的是用来保持轮廓和水平集方程的规律性.

3.3 实验及拟建模型分析

相比于C-V模型，当分割图像是无噪声分段常数时，结果是合理的.然而在大多数情况下处理的细菌图像或多或少都会受到噪声的影响.相似的，因为LBF模型可以视为C-V模型在图像所有以每个像素为中心的局部区域的应用，想要得到更加接近局部区域相应模式的fi，所以fi由方程(17)中计算得到，这也使得LCF模型对图像噪声更具鲁棒性.

对于在不同类型的细菌图像上测试了该模型.

图3显示了LCF模型的应用结果.带有噪声和灰度不均匀的细菌图像也能够拥有较精确的分割效果，其中第一行是图像的初始轮廓，第二行是LCF模型的分割结果.但是观察发现LCF模型每单次迭代所花的时间更多，但是它可以用更少的迭代次数分割细菌图像.

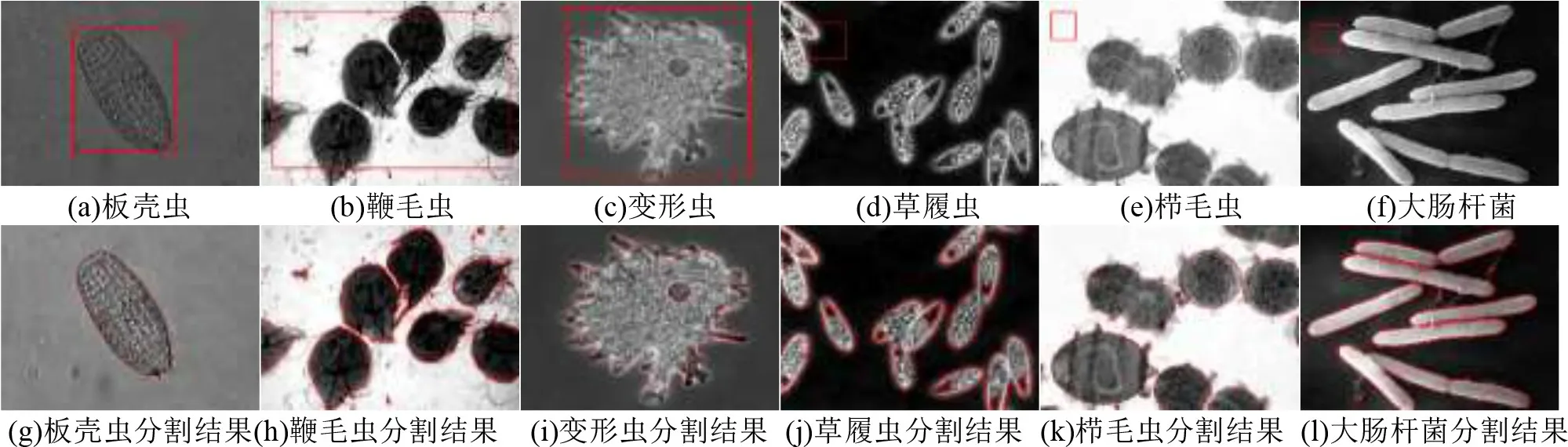
图3 各种细菌的LCF水平集分割结果Fig.3 Segmentation results of the LCF level-set for various bacteria

3.4 实验结果分析

在本节中，采用了正弦方程来表示传统主动轮廓模型中的拟合量.然后在基于水平集分割方法的基础上，应用于细菌图像局部信息的LCF分割模型.为了分割灰度不均匀的细菌图像，本节的模型达到了比二次拟合量更佳的图像处理效果，其相比传统的局部拟合量更佳温和且稳定，细菌图像上的应用结果表明该模型分割结果更加高效精确.而且与CV模型和LBF模型相比，该模型更具鲁棒性，在复杂的细菌图像的处理中计算更加高效.