世界女子硬地网球单打综合实力评价与回归模型预测分析

邹 鑫

1 研究对象与研究方法

随着社会经济水平的提高，网球项目在我国日益普及，运动健儿们在网球方面的成绩也在不断提高。值得一提的是李娜分别取得了法网以及澳网的冠军，使我国对于网球方面的重视又上升到一个新的层面，但是我们与世界最高水平的运动员比起来尚有差距［1］，我国应该采取什么样的措施和调整才能跟上世界的步伐这是一个目前急需要解决的一个难题。总体来说在现代网球比赛中一般有三种类型的场地，场地类型不但影响网球反弹和球速［2］，而且还影响战术策略的制定。本文就女子硬地单打比赛展开研究，综合前人有关我国女子硬地网球技战术方面的研究，发现一些不足之处；以几场选手比赛的数据就得出网球相关的制胜规律，选取样本不具有代表性。多数研究对影响比赛得失分的各项技战术指标相关的统计学分析较为不足。在网球技战术类相关制胜因素的研究中忽略各技战术指标的共线性问题，从而影响研究的最终结果。综合前人研究的相关问题，本文对美国网球公开赛2018-2021年女子单打64强及以后得的比赛数据进行统计分析，并分别运用因子分析法进行综合实力的评估和再用多元线性回归分析法对选手总得分进行预测，以便于备赛期间训练进行针对性训练，为我国女子网球运动员训练提供技战术方面的调整提供建议与参考。

1.1 研究对象

本文以2018、2019、2020、2021年美国网球公开赛女子单打64强及之后的比赛，共252场比赛数据为研究对象。每场比赛技术统计指标全部在美网官方网站获取，共统计如下12种原始指标；Aces（X1）、双误（X2）、一发成功率（X3）、一发得分率（X4）、二发得分率（X5）、上网得分率（X6）、破发成功率（X7）、接发球得分率（X8）、制胜分（X9）、非受迫性失误（X10）、跑动距离（X11）、总得分（X12）.

1.2 研究方法

1.2.1 文献资料法

本文通过学校图书馆查阅相关书籍分析研究意义和理论价值，以及搜集中国知网相关论文和期刊为本文研究框架的设计提供思路，并通过美国网球公开赛官网收集到第一手原始资料以及了解相关技术分析。

1.2.2 数理统计法

运用Excel2019对美网官网收集到的原始技术统计数据进行整理与分析，并将数据导入SPSS25.0软件进行降维因子分析，将十二个原始指标分成四个因子综合得分成分变量，并计算各个选手的综合比赛因子得分。以实际总得分为因变量，各技战术指标为自变量建立多元回归预测方程。

2 研究结果与分析

2.1 世界女子网球单打综合实力评价

2.1.1 单打技术间的相关性检验

表1 KMO和Bartlett球度检验

通过上表可以看出各技战术指标相关性检验是运用KMO和巴特利特球形度检验方法进行检验。测得KMO的值为0.696，由于较为接近0.7，又因为P＝0.00＜0.05，所以说明此数据适合做因子分析。

2.1.2 世界女子单打技战术因子分析

依照提取特征值大于1的原则，运用因子分析里面的主成分分析法进行提取，共取4个共性因子，经旋转后公因子1至4方差贡献率分别为20.000%、18.072%、14.683%、13.695%，四个公因子特征值分别为2.200、1.988、1.615、1.506.运用最大方差法对初始成分矩阵进行正交旋转使得更加深入了解和解释4个共性因子的实际意义。我们可以通过表3的数据得知各个技战术指标与共性因子之间的关系密切程度，相关系数越大其之间相关性越高［3］。通过对旋转后的因子成分矩阵进行分析，公因子1中按指标载荷系数从大到小分别为跑动距离，非受迫性失误，制胜分。非受迫性失误越少证明其相持能力和跑动能力越强。公因子2中按指标载荷系数从大到小排列分别为一发得分率，Aces，二发得分率，通过分析这三个指标都决定了选手发球实际得分率，所以我们把公因子2命名为发球得分效率因子。公因子3各变量指标载荷系数从小到大排列分别是一发成功率，双误，上网得分率，命名为稳定性因子。公因子4从小到大分别为破发成功率，接发球得分率，接发球得分率有与破发成功率密切相关，所以将两个技战术指标命名为破发能力因子。

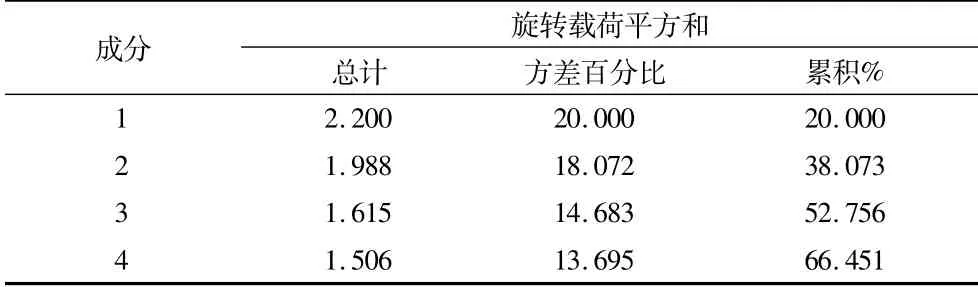
表2 旋转后各方差的解释

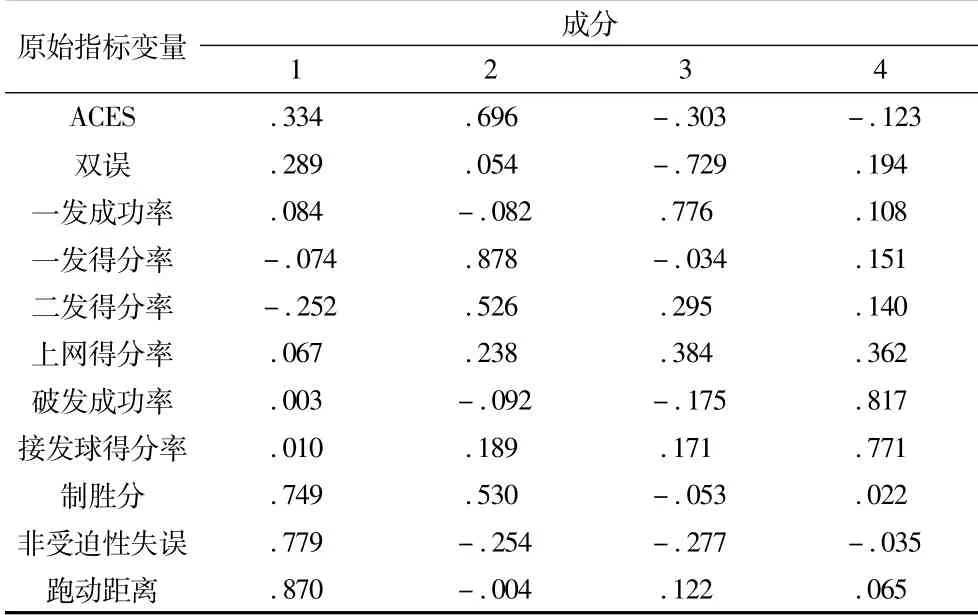
表3 女子硬地比赛数据旋转成分矩阵

表4 特征变量与因子命名

由上表中的数据可以看到与相持能力因子关联度较高的技术指标有跑动距离、非受迫性失误、制胜分。一场网球比赛需要选手全身心投入，进攻与防守只在一念之间，进攻与防守相持能力是决定比赛胜负的关键阶段［4］。在现在网球比赛中上旋打法逐渐成为主流，单打以底线相持为主。网球运动无氧供能大约占70%，有氧供能约占10%，无氧有乳酸运动占20%左右［4］，所以选手的无氧供能的能力直接影响比赛中的体能状态。跑动距离从一方面能反映出选手的体能状况以及底线相持的能力，跑动距离越远证明选手体能越好击球越稳定。如果球员在比赛中没有一点压迫和心理上的压力或者很少的情况下出现回球失误，包括下网和出界，那我们通常称这种失误为非受迫性失误［3］，非受迫性失误越多说明稳定性越差。双方球员在相持过程中通过角度调动，节奏变化等使对手没碰到球而拿下的分数叫作制胜分，这项技术指标将直接影响比赛结果的走向［5］。整场比赛制胜分的多少也从侧面体现了选手相持能力的高低，制胜分越高证明底线相持能力越强，体力越充沛。

在一场竞争激烈的网球比赛中一个好的发球显得格外重要［6］。这也是由发球球员一个人决定的技术，且网球规则赋予了运动员两次发球的可能性，使运动员在发球局阶段能够充分发挥一发球的进攻性［7］。发球得分率作为影响得分的最关键的指标之一，反映了球员发球得到综合能力以及发球之后战术衔接的完整性和有效性，是对球员的综合能力的评价指标。Aces球数量也反映了球员直接得分的能力，也是发球进攻能力的体现。

在发球基本技术中，发球是否稳定我们通过球员发球成功率就可以看出，而对发球水平的高低，发球的战术意识和发球球员的执行能是通过发球得分率来体现［8］。一直以来，发球成功率越高对接发球员造成的心理压力越大。只有较高水平的发球成功率，才可能有较高的得分率［9］。双误各数也代表了球员发球稳定性的高低，双误越少发球稳定性越高。上网得分率体现了球员准确把握上网时机的能力以及在网前稳定处理球的能力。

破发点作为比赛中的关键分，对网球比赛结果的影响大于其他分数［10］。通常一个关键分也能直接决定一场比赛的走向，要想取得一场网球比赛的胜利就要在保住自己发球局的同时破掉对方发球局，对方失误越多，你的得分越多［11］。接发球得分率是提高破发成功率与扩大局数领先的关键因素，主要体现在接发球后的相持球阶段得分。接发球与发球是一对矛盾体，发球越好对手接发越容易失误，接发越好对手发球心理压力越大。因此，在第一个比赛回合中处于主动或被动取决于接发球质量的好坏。在比赛第一回合对抗中要想处于主动，必须要有一个高质量接发。并为对方的发球造成压力，影响整局的比赛结果，与其对应的是带来接发球方的破发，因此，看以为选手的综合接发能力通过接发球局破发成功率便可看出［7］。

2.1.3 世界女子硬地单打综合单打能力因子模型构建

根据下表中的数据可以得出各因子得分模型公式为：

根据以上因子分析模型，代入各位选手的指标数据，求出WTA排名前十的各位选手的综合单打因子得分；巴蒂（1.01）、萨巴莲卡（0.92）、普利斯科娃（0.86）、穆古鲁扎（0.84）、萨拉里（0.83）、康塔维特（0.82）、贾贝乌尔（0.80）、希维翁泰克（0.76）、巴多萨（0.75），每位选手单打综合得分和现阶段排名具有高度相关性。由以上数据代入结果可以看出，通过对选手的综合得分评估可以看出此选手在此阶段的竞技状态，比起前人用年度总积分来评判选手综合实力，运用此模型计算出的因子综合得分更具有说服性和可行性。［12］。

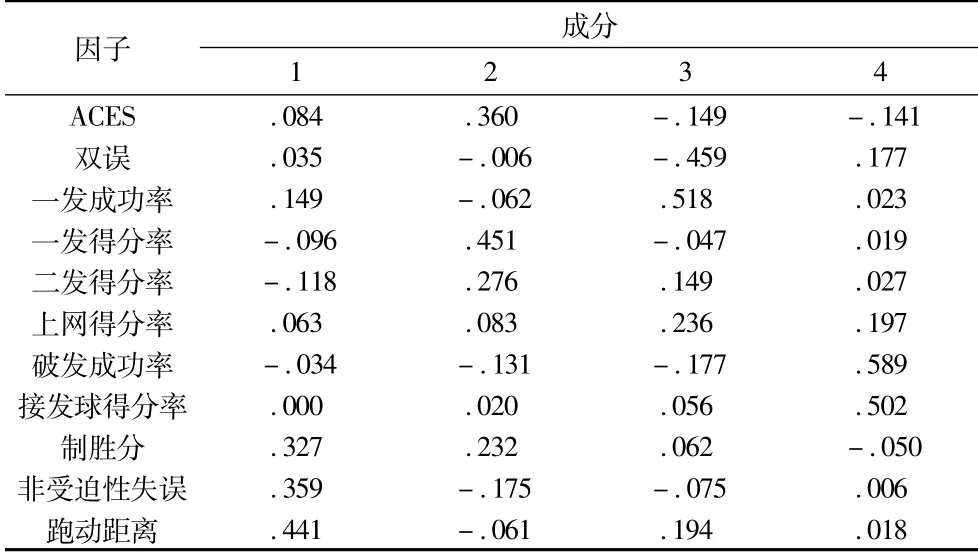
表5 女子网球硬地单打特征因子得分系数

2.2 世界女子网球单打综合实力回归模型构建

2.2.1 各技战术指标与综合因子得分相关性检验

一个事物的主要矛盾和次要矛盾往往是决定事物发展的重要因素。简单来讲运用回归分析的作用就是在多个自变量中通过一系列的回归计算，得出与因变量关系最密切的几个自变量，并用这几个自变量指标的回归系数计算出回归方程，从而使预测以后结果更为简便［12］。运用因子分析法虽然能够对选手的综合实力评价，但是较难检验选手某一项技术的优势与劣势，无法针对某一项单项技术进行改进与调整。因此把从美网官网得到的比赛总得分原始数据定义为因变量，把11项从官网搜集到的各选手的技战术指标作为自变量，我们通过逐步剔除回归分析法建立预测回归模型。从表6可以清楚的看到R值为0.925，R方值为0.855，这也比较客观的说明了方程拟合优度较好，有较强的准确性。通过表数据表明P值等于0.000，表明建立此方程很有必要且具有显著性意义。

表6 回归预测方程拟合优度检验

2.2.2 回归预测模型构建及分析

表7 回归方程方差分析表

Aces（X1）、双误（X2）、一发成功率（X3）、一发得分率（X4）、二发得分率（X5）、上网得分率（X6）、破发成功率（X7）、接发球得分率（X8）、制胜分（X9）、非受迫性失误（X10）、跑动距离（X11）、总得分（X12）.

通过对回归系数进行分析

从表8的数据中可以看出各个技战术指标的显著性检验都为显著，P值都小于0.05，所以我们对于6个变量进行保留，从而得到回归预测方程为Y＝0.012X11+0.261X4+0.492X9+0.367X8+0.2X5+0.53X1-25.02，

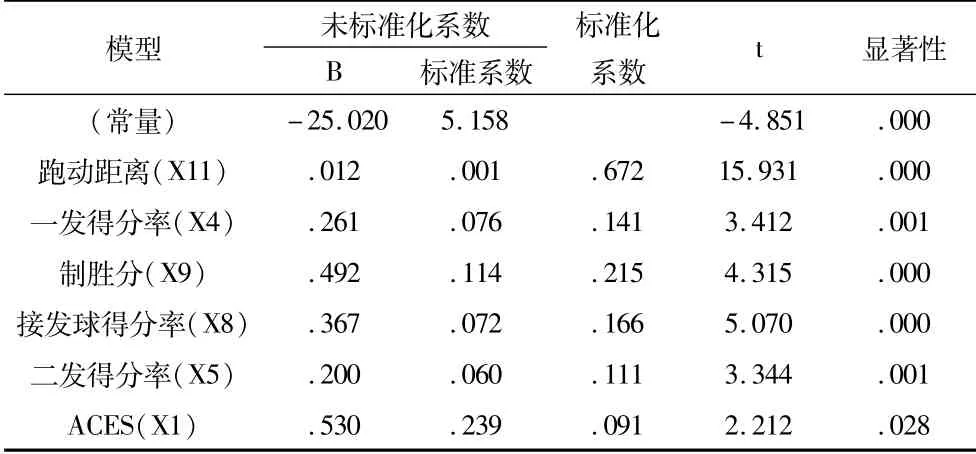
表8 回归方程模型与系数

2.2.3 回归预测模型准确度分析

本文将2021年美网女子单打16强选手的比赛原始数据代入上述的回归模型中进行回归方程准确性分析，结果如下表：

表9 回归方程预测准确度检验

通过运用Pearon方法检验实际得分与预测得分相关性，测得r＝0.977，P＝0.00＜0.05；又把实际得分和预测得分进行T检验，测得P＝0.363＞0.05，表明预测总得分对于16位选手来说还是较为准确的，预测总得分较为接近实际总得分。科贝尔预测得分91，实际得分95，准确度为0.96，穆古娜扎实际得分65，预测得分68，准确度同为0.96，以及萨巴莲卡实际得分60，得分63，准确度0.95。综合所有选手分析结果来看除斯维托丽娜和哈勒普预测准确率低于0.9，其他选手预测准确率均在0.9以上，所有选手平均预测准确率为0.94，由此可说明本文建立的预测方程具有普遍的适用性以及较高的准确性，用于预测女子单打综合实力是较为可信。

3 结论

3.1 世界女子硬地单打比赛综合实力可以分成相持能力因子、发球得分效率因子、稳定性因子、破发能力因子4个特征因子，综合得分因子模型F总（0.2F1+0.18072F2+0.14683F3+0.13695F4）／0.66451可以较为准确地评价每位女子选手的综合得分能力。

3.2 女子网球各项技术指标与总得分存在线性关系，通过原始数据建立预测回归方程Y＝0.012X11+0.261X4+0.492X9+0.367X8+0.2X5+0.53X1-25.02，方程显著性P＝0.00＜0.01，且相关性R＝0.977，通过代入16位选手原始数据进行对比，准确率为94%，该方程具有较高的拟合度和准确性，可以用本模型对女子单打运动员的比赛胜率进行预测。

3.3 结合因子分析以及多元回归模型结果来看，跑动距离和一发得分率对比赛得失分较为重要，其次为接发球得分率，Aces球和制胜分数也直接影响比赛得分数。