基于谱聚类的Kiva系统货位分配研究

杨 玮 段毅林 赵 晶 马 伟 钟名锋

（陕西科技大学 机电工程学院，西安 710021）

传统的“人到货”拣选方式中，人工劳动强度大、错误率高、拣选效率受人工经验影响大[1]。近年来具有高拣选效率、高存储密度又能降低劳动强度的“货到人”拣选系统因其能够适应订单数量高的拣选环境，成为了订单快速响应和高效精准拣选的发展趋势。谱聚类算法是一种建立在谱图理论上的聚类算法[2]，能够应对电商仓库存储货物原始数据的高维稀疏特性。

1 问题描述及基本假设

某D企业是国内领先的零售电商物流企业，其拆零拣选采用Kiva系统为主要的作业方式。该企业通过统计发现，在波次临近时间段自动导引运输车（Automated Guided Vehicle，AGV）的往返次数总是较高，导致难以保证截止订单时效。此问题的关键在于如何对现有Kiva系统中的货物进行优化分配，使具有相关性的货物能够分配到同一货架上，进而减少AGV往返次数。

现针对Kiva系统做出如下假设：第一，系统中的每一种货物只能在一个货架中存储；第二，每一个货架中能够存储的货物种类有上限；第三，每一张订单中出现的货物种类有上限。文中将要用到的变量见表1。

表1 文中参数符号及其含义

2 模型建立

以最大化货架内部所有货物的关联度之和为目标函数，根据表1中的参数构建货位分配模型，则有：

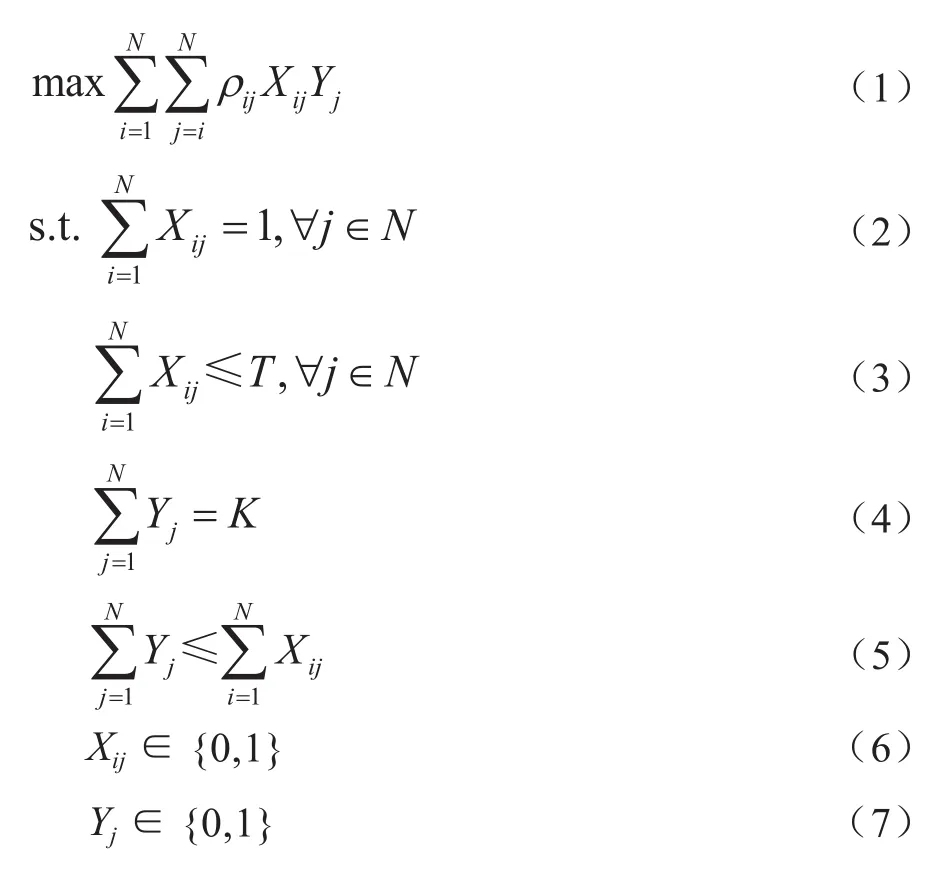
式中：目标函数（1）表示最大化货架内部所有货物的关联度之和；约束条件（2）表示一种货物只允许被分配到一个类，且必须被分配到一个聚类中心；约束条件（3）表示货架内部存储的货物数量不能超过货架的存储容量T；约束条件（4）表示聚类中心的数量等于总拣选货架数量K；约束条件（5）表示聚类中心数量应不多于所存储的其他货物类别的数量；约束条件（6）和约束条件（7）表示决策变量为0-1变量。

货架之间的相关性由各货架上存储的所有货物的总相关性决定，对货架内部所有货物之间的相关性进行叠加即可求得货架间的相关性。任意两个货架之间的关联度σkk´表示为：

3 模型求解

3.1 谱聚类算法

谱聚类算法的实质是把原来的聚类问题转变为图的最优划分问题[3]，因此可以将谱理解为矩阵的特征值的集合[4]，将以前的点对点局部聚类方法转化成图的相关知识，然后利用图论中的最优划分策略来解决点的聚类问题。与传统的K-means算法相比，该算法能更好地适应数据分布，聚类效果更加出色。

采用谱聚类算法求解的货物分配步骤如下：

（1）根据历史订单数据统计分析不同货物品类被订购的频率，以此计算货物i和j之间的关联关系；

（2）根据分类数量等约束条件和货物品类之间的关联关系，对货物进行聚类；

（3）将货物合理地放置到每个货架中；

（4）按照货架关联度计算公式，计算系统中所有货架之间的关联度；

（5）按相关性将每组货架完成分组。

整个货位分配流程图如图1所示。

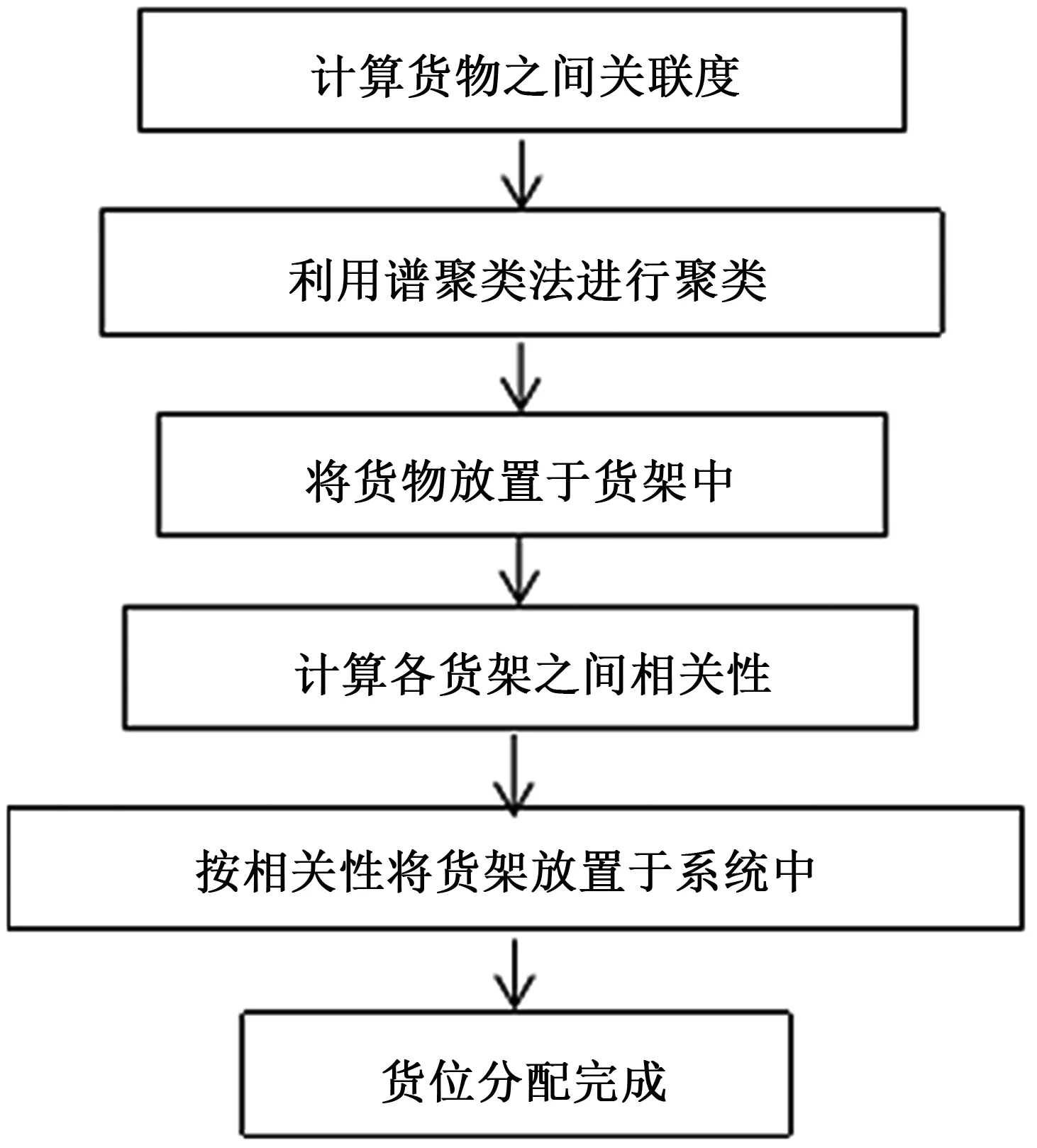
图1 Kiva系统货位分配流程图

3.2 货位分配效果评估

对Kiva系统进行货位分配后，与原始货位分配方案进行对比。通过比较两者系统中AGV小车的往返次数来对货位分配结果进行评估，则有：

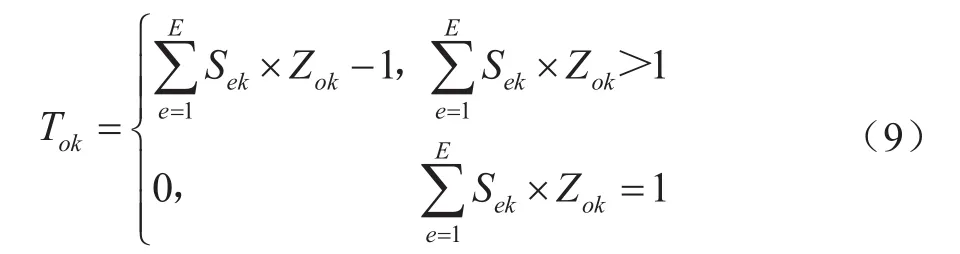
式（9）表示每个订单在任意一个货架到来时能够节省的AGV往返次数。其中：e∈E，表示货物；o∈O，表示订单；k∈K，表示货架；Sek=1，表示货架k包含货物e；Sek=0，表示货架k不包含货物e；Zok=1，表示货架k中有订单o中的货物；Zok=0，表示货架k中没有订单o中的货物。

完整的货位分配过程能够节约的AGV往返总次数可以表示为：

4 实例分析

4.1 实例介绍

某D企业拥有的Kiva系统拣选区的货架共有300个。货架按照2×5的组合方式布置，总共有30个货架集群，如图2所示。

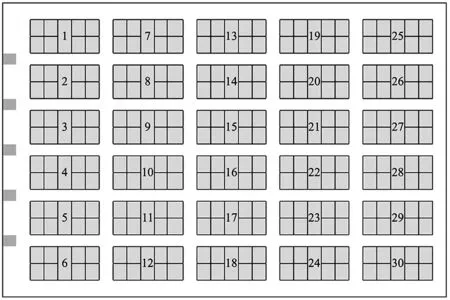
图2 某D企业Kiva系统货架布置图

根据企业要求，货物的类别和名称都用相应的数字编码代替。表中共有1 688张订单数据，根据统计分析，订单中包含最少的货物种类数量为1，最多的种类为35，订单中包含的货物种类总共为1 200种，具体订单信息如表2所示。

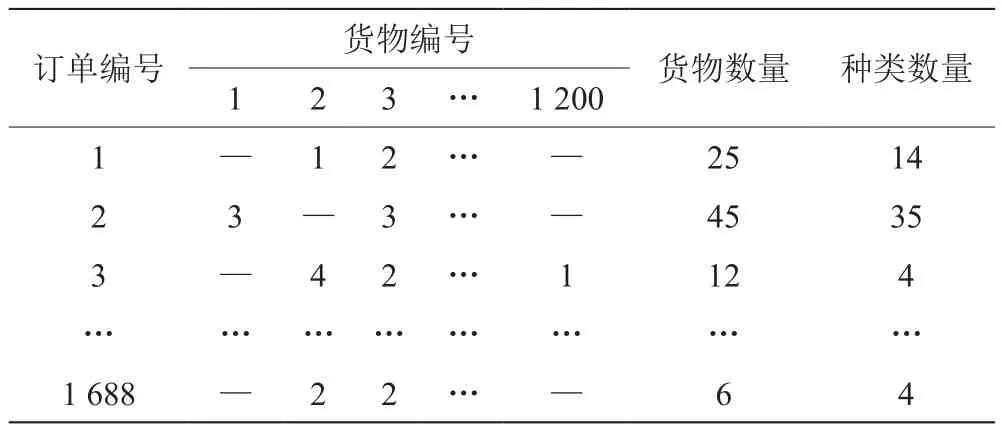
表2 订单数据

4.2 结果分析

通过对历史订单数据进行分析，统计各种货物出现的频次，计算求得1 200种货物之间的关联度，从而得到所有货物之间的相似度矩阵如表3所示。

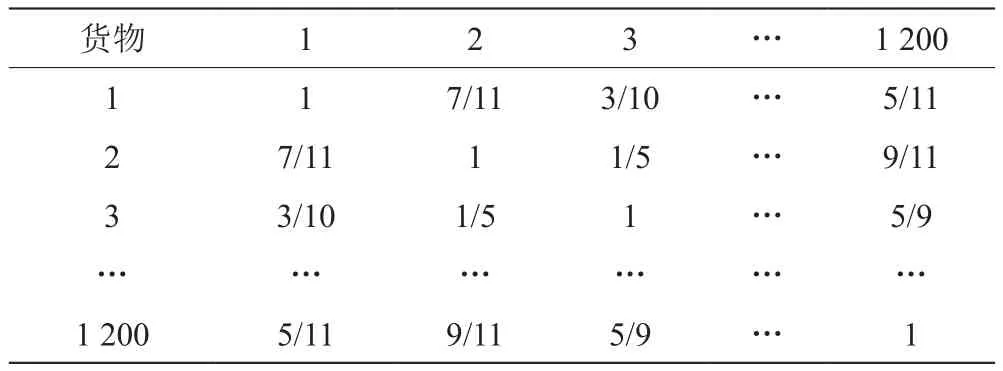
表3 1 200种货物间的相似度矩阵

在计算过程中，结合企业实际的货架存储情况，规定N=4为每个货架内部存储的货物种类数量。此外，规定将聚类中心的数量设定为与货架的总数相同的值300，最终得到货物聚类分析的结果如表4所示。

表4 货架中货物聚类结果

由表4可知，每个货架中存放4种货物，并且这4种货物之间的关联性较大，订单中的1 200种货物根据其相关性被分配在300个货架中。

货架之间的相关性由存储在货架内部的货物之间的关联性所决定，300个货架两两之间的关联程度等于货架内部所有货物之间的相关性总和，求解结果如表5所示。

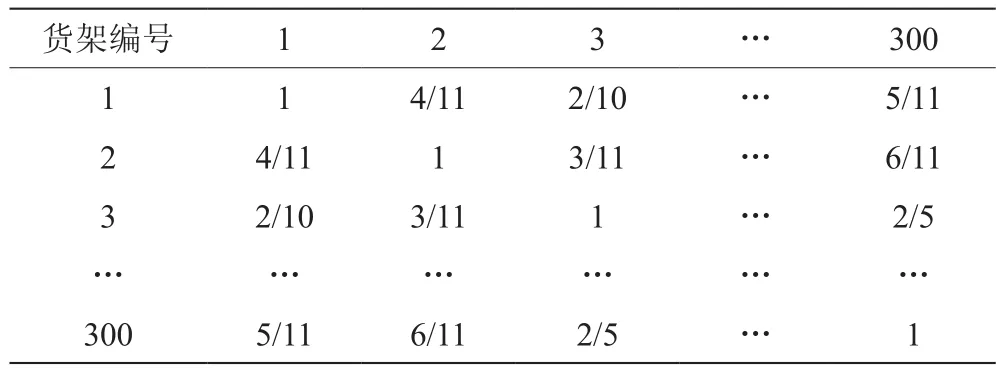
表5 300个货架两两之间的关联程度

根据1 200种货物的聚类结果以及300个货架间的关联程度，完成对整个Kiva系统中的货位分配，聚类的结果按货架从左至右从上至下布置，分配结果如表6所示。

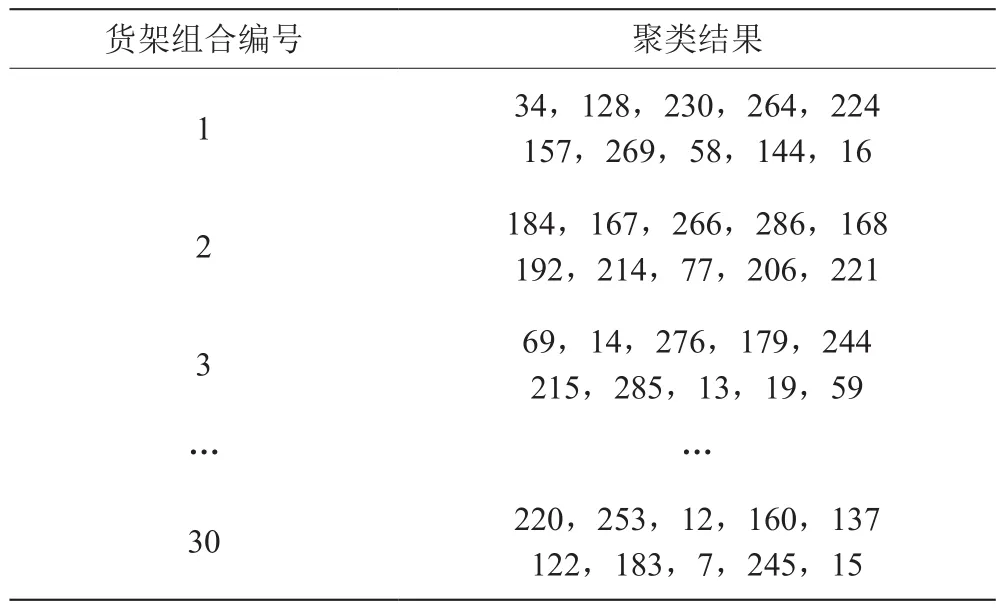
表6 货位分配结果

4.3 效果评估结果

选择该企业临近波次时间段内的40张订单进行分析，这40张订单中最多的一张订单包含有17种货物，具体的订单信息如表7所示。

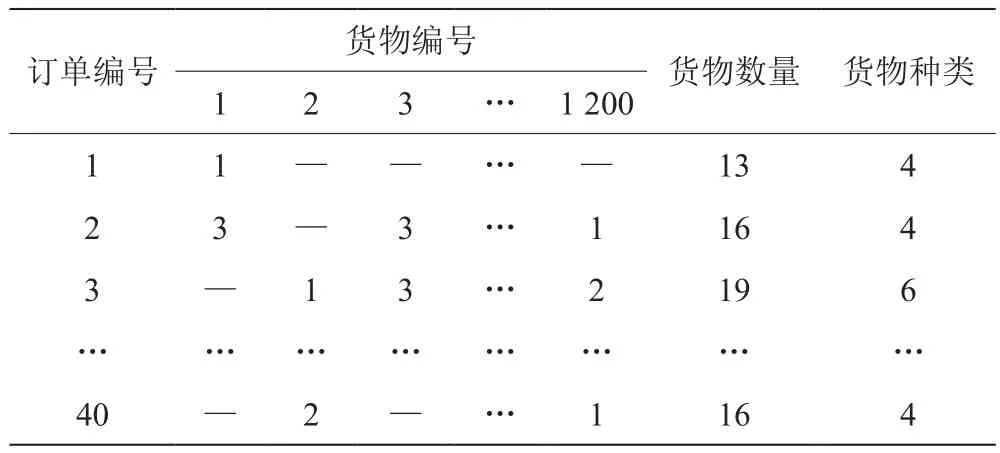
表7 40张订单数据

对这40张订单采取企业原始的固定货位策略以及本文提出的货位关联分配策略这两种策略进行拣选。统计拣选完这40张订单后AGV的往返次数，将采用MATLAB 2016a编程运算求得的结果与原始固定货位相比，进行货位分配作业之后各自的AGV的往返次数如表8所示。

表8 货位分配效果评估模型计算结果

由案例分析结果可知，对于临近波次拣选的40张订单来说，与原始固定货位分配相比，采用本文所构建的货位分配模型对Kiva系统中的货物进行货位分配之后，AGV小车由原先的106次往返降低到61次，节约往返次数45次，往返次数减少了42.45%。

5 结语

本文以某D企业实际的Kiva系统为研究对象，针对Kiva系统中货位分配问题，构建货位分配模型。根据历史订单数据分析货架中货物的关联关系，使用谱聚类算法进行聚类分析，并将相关性较大的货物存放在同一个货架上。在此基础上分析各个货架之间的关联关系，构建货位分配效果评估模型，并使用MATLAB编程运算求得采用货位分配算法之后与原先的货位分配方式所节约的AGV往返次数。优化结果表明，所采用的货位分配算法能够有效地减少AGV的往返次数，更好地适应临近波次的任务紧急性，提升仓库作业效率。