轧机主传动机电耦合系统自抗扰控制器设计

2022-01-14梁卫征曹志新张瑞成

现代制造技术与装备 2021年12期

梁卫征曹志新张瑞成

（华北理工大学电气工程学院，唐山 063210）

轧机振动问题由来已久，一直是制约轧制高强薄板和高附加值产品的瓶颈。板带轧机是一种大型复杂的机电液一体化生产设备。为提高轧制效率、改善产品质量，文献[1]建立了轧机主传动系统机电耦合模型，利用数值方法分析了漏磁系数、空气摩擦等因素对轧机振动的影响；文献[2]从机理上分析了机电耦合因素对主传动系统扭转变化的影响。然而，导致轧机振动的因素是复杂多样且相互耦合的，无法从根源上彻底消除轧机振动，因此设计一种具有较强鲁棒性和抗干扰能力的控制系统显得尤为必要。

自抗扰控制技术（Active Disturbance Rejection Controller，ADRC）在面对外部复杂多变的干扰时具有良好的控制效果和强大的自适性。目前，该技术在电机调速系统和运动控制等领域都取得了一些显著成果[3-5]，但在轧机主传动机电耦合系统振动的控制领域展开具体研究和深入分析的成果还不多。针对轧机主传动机电耦合系统中出现的振动，利用ADRC方法设计了轧机主传动机电耦合自抗扰控制系统，进行了相应的仿真研究，并与传统比例-积分-微分（Proportion Integration Differentiation，PID）控制进行了相互比较，取得了显著的控制效果。

1 轧机主传动机电耦合模型的建立

将轧机主传动系统简化为两自由度弹簧系统，直流电机-轧机主传动机电耦合系统模型如图1所示。

图1 轧机机电耦合系统模型示意图

图1中：J1、J2为电机和负载的转动惯量；M1、M2为电机输出的电磁转矩和负载转矩；K、C1为弹性轴刚度系数和阻尼系数；ω1、ω2为电机和负载的角速度；θ为相对旋转角度。文献[6]建立了系统的数学模型：

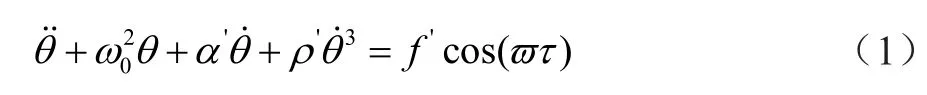
式中：J=J1+J2；

2 轧机主传动机电耦合系统ADRC设计

定义综合扰动项a(t)为：

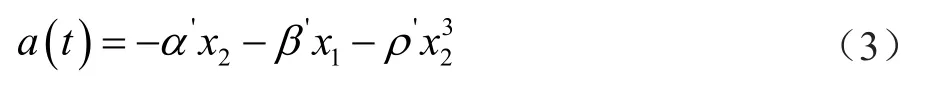
其对应的自抗扰控制系统结构如图2所示。

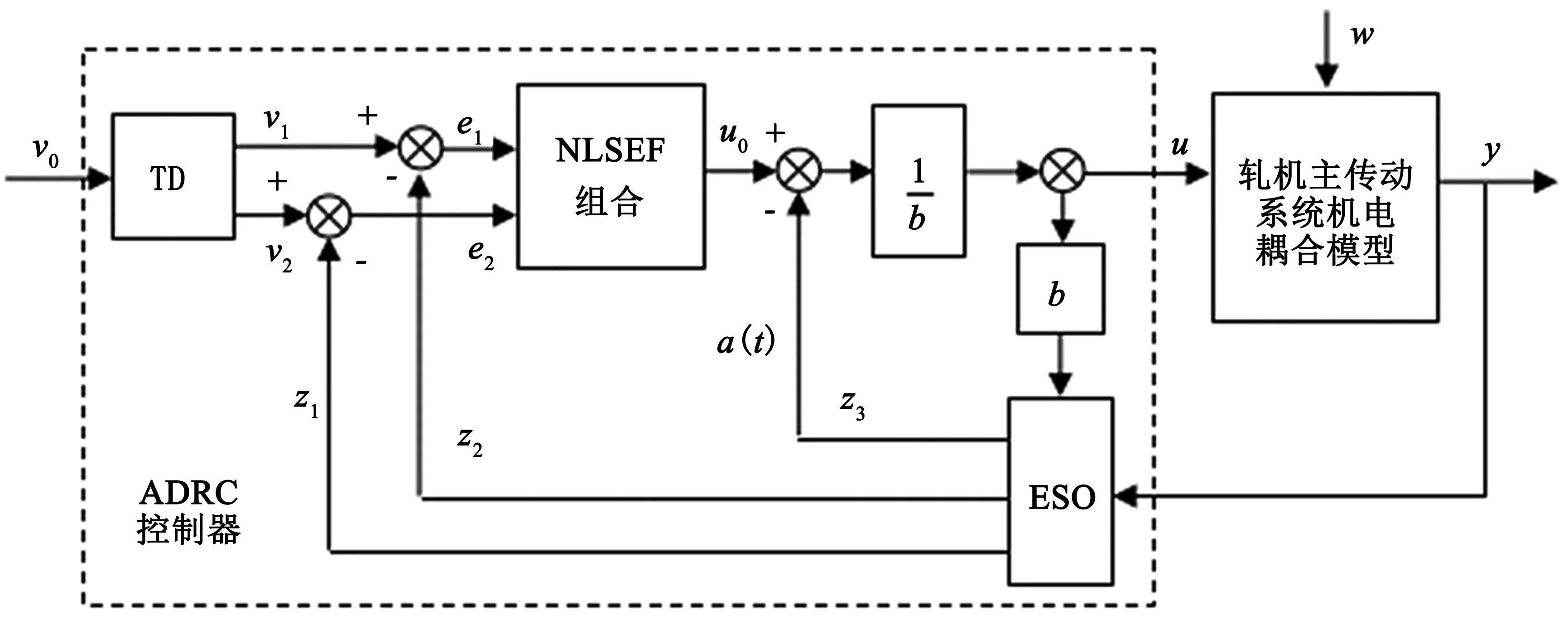
图2 轧机主传动机电耦合自抗扰控制系统

2.1 跟踪微分器

v0(t)为控制目标，v1(t)为安排的过渡过程，v2(t)为过渡过程的微分信号：

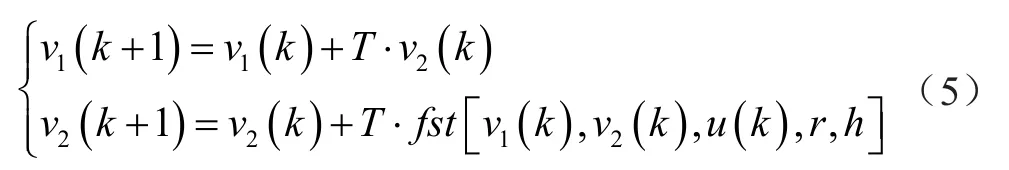
式中：T为采样周期；u(k)为第k个采样时刻的控制信号；r为影响跟踪快慢的参数；h为决定滤波效果的参数；fst(r,h)为最速综合函数。

2.2 扩张状态观测器

扩张状态观测器负责观测系统状态和综合扰动项a(t)，其表达式为：

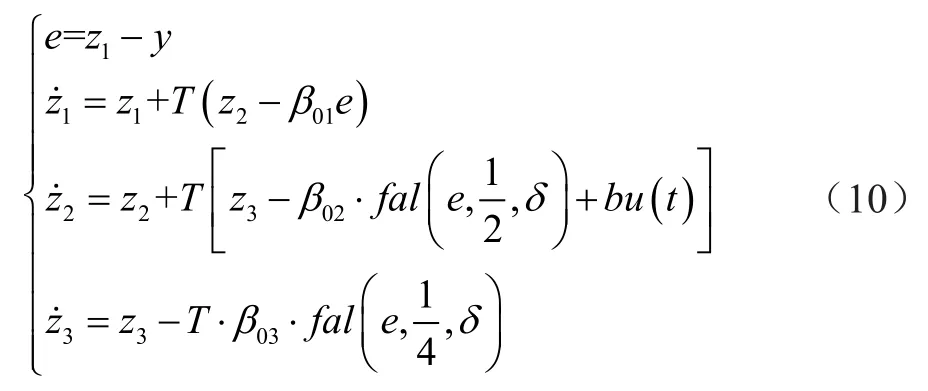
2.3 非线性控制率

非线性控制率的表达式为：

式中：e1、e2是误差和该误差的微分，实际控制u中的-z3/b项补偿扰动和未建模动态特性。

3 轧机主传动机电耦合系统ADRC仿真

3.1 抗干扰实验

以某2 030 mm型冷轧机系统参数为例进行仿真实验。ADRC参数选取分别为：r=22，h=0.01，T=0.01，a=[0.75，1.25]，b=1，δ=0，β01=200，β02=100，β03=20，β1=180，β2=120。

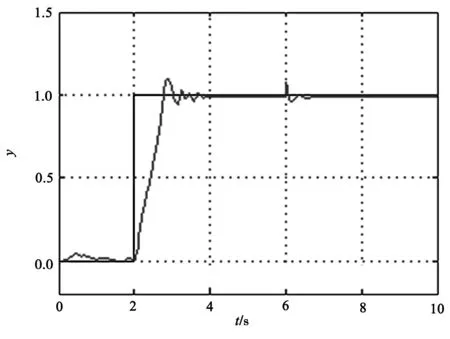
图3 系统响应曲线

3.2 鲁棒性实验

将轧机负载转动惯量增大一倍，不改变控制器的其他参数，经计算得系统参数为：ω0=1，α=0.53，ρ=0.26，f=0.62，ε=0.02。通过仿真实验得到系统经过自抗扰控制（实线）和PID控制（虚线）后系统的鲁棒性能对比图如图4所示。由图4可见，自抗扰控制器能够使系统迅速地恢复到稳定的状态，且超调量小、调节时间短，控制效果优于PID控制。