门座(桥架)起重机动态电子秤测量结果的不确定度分析与评定
2022-01-14张楠丽ZHANGNanli姚帅YAOShuai
张楠丽 ZHANG Nan-li;姚帅 YAO Shuai
(广东省计量科学研究院,广州510405)
0 引言
门座(桥架)起重机动态电子秤,简称门桥秤,是一种自动分检衡器,原理是起重机在提升或变幅抓取货物的过程中,通过称重传感器检测钢丝绳的受力,由位移传感器和速度传感器等检测幅度及速度,经称重指示器显示被称物的重量值[1]。门桥秤是港口码头、铁路运输、工厂仓库等场所中常见的设备,主要应用于物品的装卸称重计量,可以避免利用电子汽车衡称重的繁杂流程,其准确性关系到轮船、火车和货车等交通运输工具的载重控制,是其计量控制中的重要的环节[2]。测量过程中的测量结果不可避免的具有不确定性,若要完整地对测量结果的质量有个定量的描述,就应当进行测量不确定度分析与评定。在检定规程JJG 1124-2016《门座(桥架)起重机动态电子秤》中,对门桥秤的动态检定提出了检定要求,检定过程中需要进行两种称量试验,分别是单次称量和累计称量,本文就门桥秤的检定两种称量试验的测量结果进行不确定度评定。
1 测量依据和方法
1.1 测量依据
JJG 1124-2016《门座(桥架)起重机动态电子秤》
1.2 被测对象
门座(桥架)起重机动态电子秤,测量范围:(500~20000)kg,检定分度值 e:50kg,准确度等级:Y(b)。
1.3 检定方法
1.3.1 单次称量
单次称量采用直接加载砝码,即用门桥秤,以最大提升速度提升砝码,进行至少5 次称量,记录每次称量示值。检定规程中要求至少选择四个不同的秤量点进行检定,本次不确定度分析以其中一次秤量点为例,按公式(1)计算单次称量示值误差。
1.3.2 累计称量
记录累计重量的开始示值TS,在起重机最大提升速度下,至少进行10 次单次称量,记录累计称量结果TE。再把这10 次称量的所有检定载荷放到控制衡器的承载器上进行称量LT,确定约定真值。则可按公式(2)计算累计称量的示值误差。
2 测量模型及不确定来源分析
2.1 测量模型
2.1.1 单次称量的示值误差可以用公式(1)表示

式中:
E——单次称量示值误差,kg 或t;
I——称量示值,kg 或t;
M——载荷,kg 或t。
2.1.2 累计称量的示值误差可以用公式(2)表示

式中:
Esep——累计称量示值误差;
TS——累计称量开始时的累计示值,kg 或t;
TE——累计称量结束时的累计示值,kg 或t;
LT——控制衡器的示值,kg 或t。
2.2 方差和传播系数
2.2.1 方差
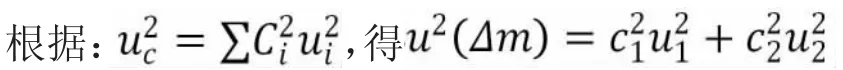
式中:
u1——I 的不确定度;u
2——M 的不确定度。
2.2.2 传播系数
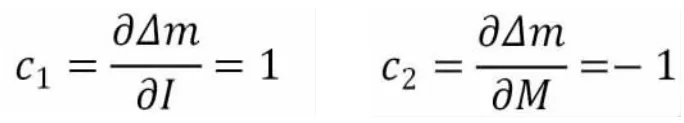
2.3 不确定度来源分析
门桥秤测量结果不确定度来源主要包括:
①重复性条件下门桥秤的重复性;
②门桥秤的分辨率;
③标准器(砝码或控制衡器)的示值不准;
④测量方法与规定测量方法和程序的不一致性;
⑤人员误差的存在;
⑥环境(如振动、干扰等)对测量结果的影响。
在参考条件下,由于检定时间较短,环境是相对稳定的,可不必考虑上述不确定度来源较小的④、⑤,⑥属于高阶小量,可以忽略不计。所以本次不确定度分析的重点是①、②、③。
3 标准不确定度分量的评定
3.1 门桥秤单次称量的测量不确定度分析
3.1.1 门桥秤的重复性导致的A 类测量不确定度分量u1
对门桥秤在起重机最大提升速度下,在重复性测量条件下,重复测量10 次。

采用贝塞尔公式得到单次实验标准偏差:

以平均值的实验标准偏差作为测量结果的标准不确定度,则A 类标准不确定度:
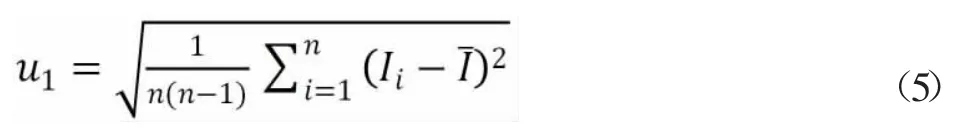
自由度:
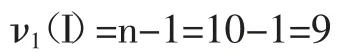
3.1.2 门桥秤数字示值分辨率带来的测量不确定度分量u2
由于门桥秤在进行动态的单次称量时,无法采用“闪变点法“确定门桥秤的化整前的示值误差,则门桥秤的分辨率导致的不确定度分量u2:
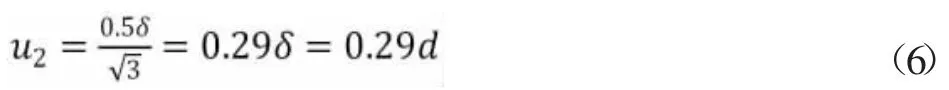
3.1.3 砝码的质量误差带来的测量不确定度分量u3
静态载荷是由砝码组合而成,误差按均匀分布处理。则:

3.1.4 合成标准不确定度的评定
输入量I 和输入量M 相互独立不相关,故合成标准不确定度uc:

3.1.5 扩展不确定度的评定
取k=2,置信概率p=95%,则扩展不确定度:

3.1.6 标准不确定度一览表(表1)

表1 单次称量
3.2 累计称量的测量不确定度分析
3.2.1 由重复性误差带来的不确定度分量u1
在起重机最大提升速度下,对同一载荷进行10 次单次称量,由于10 次载荷为同一载荷,控制衡器为电子汽车衡,其重复性为R,根据检定规程JJG 539-2016《数字指示秤》[3],重复性试验中,重复性次数一般为3 次。依据JJF 1059.1-2012《测量不确定度评定与表示》,一般在测量次数较少时,可以采用极差法评定获得试验标准偏差,查JJF 1059.1-2012《测量不确定度评定与表示》[3]得3 次测量次数对应的极差系数C=1.69,则控制衡器的重复性误差带来的不确定度分量u1。

3.2.2 门桥秤数字示值分辨率带来的测量不确定度分量u2
由于在进行门桥秤的累计称量检定时,无法采用“闪变点法”确定门桥秤化整前的示值误差。所以采用直接读数法,门桥秤的分度值d,其数字示值的分辨率为1.0d,则门桥秤的分度值导致的不确定度分量u2:
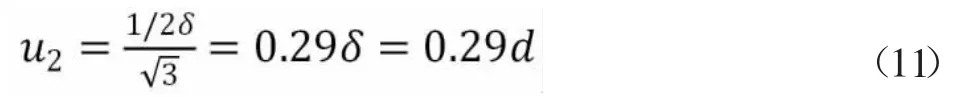
3.2.3 控制衡器示值误差带来的测量不确定度分量u3
使用控制衡器确定累计的载荷质量的约定真值,如果使用准确度较高的控制衡器,其分度值较小、分度数较多,并且在稳定的环境条件情况下使用,则控制衡器示值误差带来的测量不确定度可以采用B 类方法进行评定,控制衡器的分度值为d1,采用直接读数法,分布作为均匀分布,则测量不确定度分量u3:

3.2.4 控制衡器允许误差带来的测量不确定度分量u4
输入量由控制衡器示值误差引起的标准不确定度分量u4,主要由数显装置化整引起,采用B 类方法进行评定,分布为均匀分布若合格的控制衡器的最大允许误差为MPE,测量不确定度分量u4:

3.2.5 合成标准不确定度
输入量和输入量相互独立不相关,故合成标准不确定度uc:
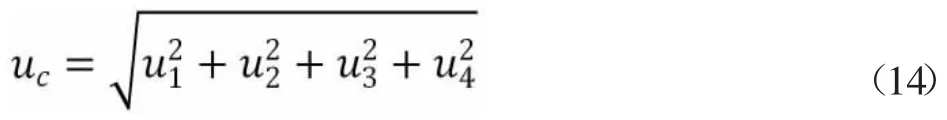
3.2.6 扩展不确定度的评定
取k=2,置信概率p=95%,则扩展不确定度:
U=uc,k=2
3.2.7 标准不确定度一览表
如表2 所示。
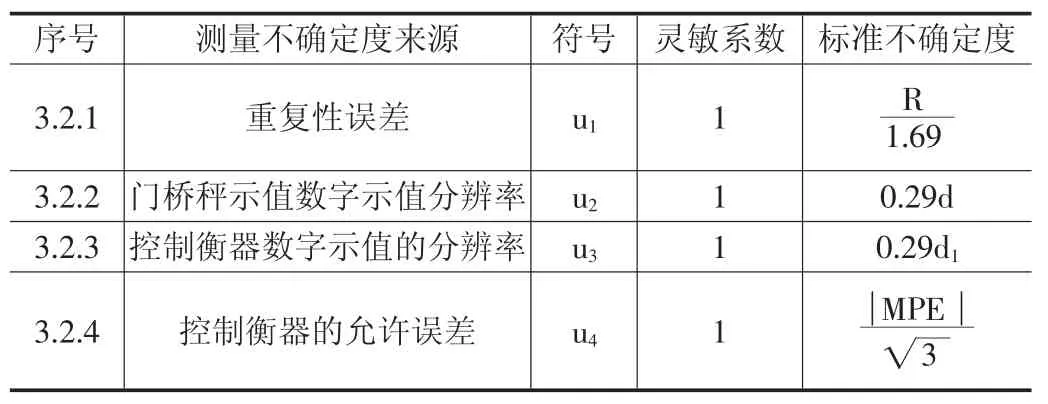
表2 累计称量
4 测量不确定度的评定示例
若对一台Y(b)级的门座起重机动态电子秤进行检定,最小秤量Min=500kg,最大秤量Max=20000kg,检定分度值e=d=50kg。在秤量点为12000kg 进行重复次数为10次的单次称量检定。进行一次累计称量,门桥秤的累计示值为120100kg。控制衡器为Max1=60t,d1=20kg 的电子汽车衡,通过控制衡器确定的累计称量的累计载荷约定真值为120000kg。
4.1 单次称量的测量不确定度
4.1.1 门桥秤的重复性导致的A 类测量不确定度分量u1
对门桥秤在起重机最大提升速度下,在重复性测量条件下,重复测量10 次,得到测量如下数据:12050kg、12000kg、12000kg、12000kg、12050kg、12000kg、12050kg、12000kg、12000kg、12000kg、12000kg。10 次测量结果的平均值为 12015kg,按照公式(4):
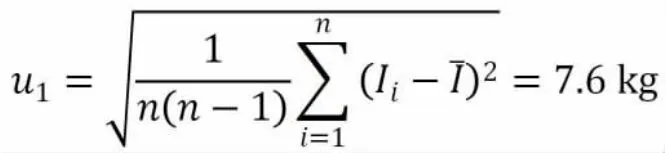
4.1.2 门桥秤数字示值分辨率带来的测量不确定度分量u2
门桥秤的分度值d=50kg,按照公式(6):
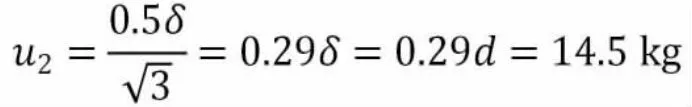
4.1.3 砝码的质量误差带来的测量不确定度分量u3
10000kg 的静态载荷通常是由12 个1000kg 的M1级砝码组合而成。一个1000kg 的M1级砝码的允差为50g。12 个1000kg 的砝码示值相关,误差按均匀分布处理。则:

4.1.4 标准不确定度的合成
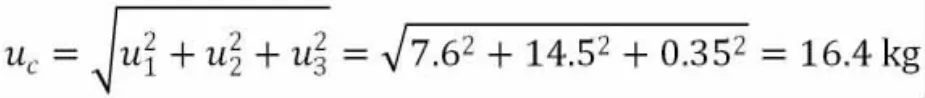
4.1.5 扩展不确定度
取k=2,则扩展不确定度:
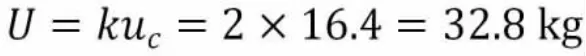
4.2 累计称量的测量不确定度
4.2.1 由重复性误差带来的不确定度分量u1
在起重机最大提升速度下,对同一载荷进行10 次单次称量,由于10 次载荷为同一载荷,控制衡器为Max1=60 t,d1=20kg 的电子汽车衡,其重复性为R=4kg,按照公式(10):
4.2.2 门桥秤数字示值分辨率带来的测量不确定度分量u2
门桥秤的分度值d=50kg,按照公式(11):
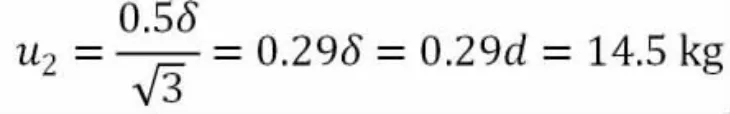
4.2.3 控制衡器示值误差带来的测量不确定度分量u3
控制衡器的分度值为d1=20kg,按照公式(12):
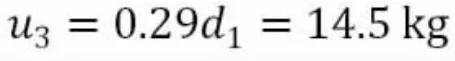
4.2.4 控制衡器允许误差带来的测量不确定度分量u4
控制衡器在12000kg 处的最大允许误差MPE 为±20kg,按照公式(13):
4.2.5 标准不确定度的合成
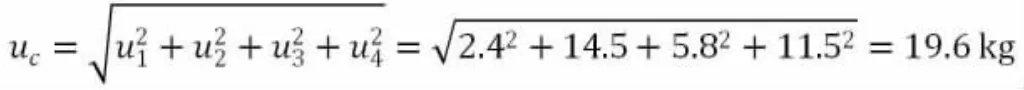
4.2.6 扩展不确定度
取k=2,则扩展不确定度:
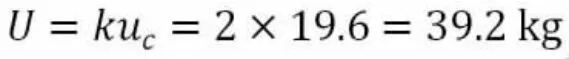
4.3 测量不确定度的汇总
依据JJF1094-2002《测量仪器特性评定》[5],测量不确定度与最大允许误差之间有一个可以接受的原则是:其扩展不确定度U 应不大于被测衡器最大允许误差的绝对值MPEV 的
Y(b)级,Max=20000kg,e=50kg 的门桥秤,单次称量检定时在12000kg 称量处的最大允许误差为单次称量的测量结果的扩展不确定度U(k=2)=32.8kg<所以符合要求。
Y(b)级的门桥秤在进行累计称量检定时,累计载荷120100kg 时,最大允许误差累计称量的测量结果扩展不确定度U(k=2)=39.2kg <,所以符合要求。
5 结束语
本文结合检定规程和实际检定,对门座(桥架)起重机动态电子秤的测量不确定度的进行了分析和评定。通过对Y(b)级门桥秤,单次称量和累计称量的不确定度来源的评定,得到了单次称量和累计称量的测量结果的扩展不确定度,分别小于门桥秤单次称量和累计称量最大允许误差的三分之一,门桥秤单次称量和累计称量的扩展不确定度符合要求。在实际使用和检定门座(桥架)起重机动态电子秤过程中,发现偏载也会对其测量结果有影响,但由于规程没有对偏载没有要求,没要求进行偏载试验,故未考虑偏载对测量结果的影响。
