一种改进的信号子空间聚焦宽带DOA 估计算法
2022-01-14贾思宇丁华泽赵鲁阳
贾思宇,路 茗,丁华泽,陈 明,赵鲁阳
(1.中国科学院上海微系统与信息技术研究所无线传感网与通信重点实验室,上海 200050;2.上海科技大学信息科学与技术学院,上海 201210;3.中国科学院大学,北京 100049;4.中国科学院无锡高新微纳传感网工程技术研发中心,江苏无锡 214135)
0 概述
基于传感器阵列的波达方向(Direction of Arrival,DOA)估计被广泛应用于生产生活中[1],例如雷达、声呐、地震勘探、导航、声源跟踪等[2-4]。现有DOA 估计算法大多假设被测信号是窄带且噪声服从高斯分布[5],并利用多重信号分类[6-7](Multiple Signal Classification,MUSIC)算法进行估计,因此,在处理宽带信号源时的性能受自然界声波、地震波等因素[8-10]限制。
宽带信号DOA 估计算法主要分为非相干信号子空间算法[11-12]和相干信号子空间算法[13-14]。非相干信号子空间算法仅分辨非相干信号,并且在低信噪比条件下估计性能不佳;相干信号子空间算法可用于相干信号,在低信噪比条件下估计准确度高,但其聚焦过程运算量较大且性能受波达角度预估计偏差的影响,波达角度预估计结果较差时会导致性能严重下降[15]。文献[16]提出一种投影子空间正交性测试(TOPS)算法,利用多个频点子空间的正交性实现宽带信号DOA 估计,但其估计精度不高且易出现伪峰。文献[17]提出修正的TOPS 算法,利用信号子空间投影有效剔除伪峰,但其在低信噪比条件下估计性能不佳。文献[18]根据宽带阵列导向矢量在法线方向上的频率一致性,提出基于频域时延补偿的DOA 估计算法,该算法性能优,但计算量较大。文献[19]采用接收到的数据构造聚焦矩阵以避免DOA 预估计,但估计性能依赖聚焦频率的选取。文献[20]利用阵型中理想的低秩Toeplitz 结构,在快拍数不足的情况下实现DOA 估计,但该方法需要求解半定规划问题且计算复杂度较高。文献[21]提出信号子空间聚焦(Focusing Signal Subspace,FSS)算法,将参考频率的信号子空间特征向量和其他频率的信号子空间特征向量结合到Frobenius 范数的约束中,实现聚焦矩阵的构造,该算法分辨率高且均方根误差低,无需进行初步的DOA 估计,但在短快拍条件下性能不佳。
本文提出一种改进的信号子空间聚焦算法MFSS。根据子频带波长间隔与半波长的匹配度选取最佳参考频率及子频带,减少聚焦过程的运算量,同时将协方差矩阵平均处理为Hankel 矩阵并进行奇异值分解重构,降低噪声及短快拍对协方差矩阵的影响。在此基础上,利用信号子空间聚焦构造最终的聚焦协方差矩阵,并通过Root-正交传播算子实现DOA 估计。
1 宽带信号模型
均匀线阵模型如图1 所示。假设有P个相互独立的远场宽带相干信号以角度θ1,θ2,…,θP入射到M个阵元的均匀线阵上,阵元间隔d为信号最高频率对应的半波长。

图1 均匀线阵模型Fig.1 Model of uniform linear array
第m个阵元接收的信号如式(1)所示:

其中:sp(t)为阵元接收的第p个信号;nm(t)为第m个阵元接收的噪声;τmp为第p个信号到达第m个阵元较到达第1 个阵元的延迟。τmp如式(2)所示:

其中:c为信号传播速度。
均匀线阵模型对接收数据xm(t)做离散傅里叶变换,将其划分为J个子带,快拍数为K,如式(3)所示:
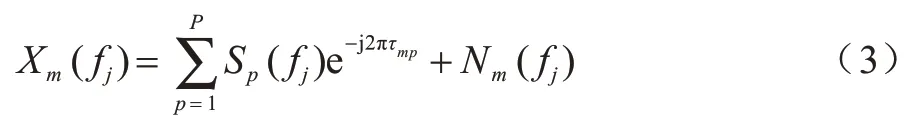
矩阵形式的频域阵列信号接收模型如式(4)所示:

其中:A(fj,θ)为阵列流型矩阵。列向量α(fj,θp)如式(5)所示:

X(fj)的协方差矩阵如式(6)所示:

其中:Rs(fj)、Rn(fj)分别为频率上信号与噪声的协方差矩阵。因此,Rs(fj)如式(7)所示:

2 基于MFSS 的宽带信号DOA 估计
2.1 FSS 算法
FSS 算法的原理是结合参考频率和其他频率信号子空间的特征向量,在Frobenius 范数约束下构造聚焦协方差矩阵,采用MUSIC 算法实现DOA 估计。
FSS 算法对R(fj)进行特征分解,如式(8)所示:

其中:U(fj)为R(fj)的M×M维的特征向量矩阵;U(fj)=[e1(fj),e2(fj),…,eM(fj)]。由于信号与噪声相互独立,则信号子空间Us(fj)、噪声子空间Un(fj)分别如式(9)、式(10)所示:

FSS 算法构造非奇异矩阵T(fj),将其作为聚焦矩阵,Us(fj)如式(11)所示:

为获得最小的聚焦误差,FSS 算法使用Frobenius范数约束信号子空间,如式(12)所示:

其中:T(fj)为Hermitian 矩阵。因此,聚焦矩阵T(fj)满足式(13):

将式(12)重写为:

矩阵C如式(15)所示:

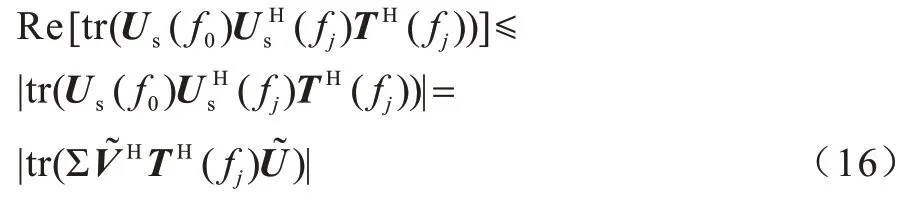

当|Zii|=1,i=1,2,…,M时,式(17)可取最大值,此时:

则频率fj处的聚焦协方差矩阵如式(20)所示:
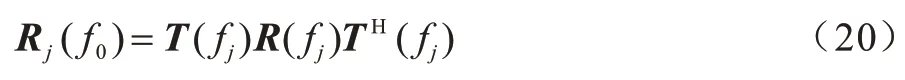
最终的协方差矩阵RF是子频带的聚焦协方差矩阵的均值,如式(21)所示:

最后,通过MUSIC 算法实现DOA 估计。
2.2 MFSS 算法
MFSS 算法是将宽带信号分为J段并进行傅里叶变换,通过计算子频带波长间隔与半波长的插值选定参考频率,并筛选出3 个子频带,将子频带的协方差矩阵处理为Hankel 矩阵,采用奇异值分解去噪并重构协方差矩阵,利用信号子空间聚焦法构造聚焦协方差矩阵并通过Root-正交传播算子得到DOA估计值。MFSS 算法流程如图2 所示。

图2 MFSS 算法流程Fig.2 Procedure of MFSS algorithm
2.2.1 参考频率及子频带选取
对于J个子频带,MFSS 算法计算频率,其中c为速度,阵元间隔。在子带1,2,…,J中,MFSS 算法搜索波长间隔最接近正整数j0=的子带,其中mod 表示余数,fs为信号的采样频率。由于每个子频带信号的波长是不同的,因此MFSS算法需选取一个子频带与该波长间隔最为匹配。
MFSS 算法选取该子频带的中心频率f0作为参考频率,使用该子频带及临近两条子频带进行后续的计算估计,临近的两条子频带频率为fξ,ξ=1,2。
2.2.2 协方差矩阵重构
在实际工程中,协方差矩阵由有限数量采样条件下获得接收数据的平均值构成,且噪声形式复杂。这些因素都会导致特征分解时信号子空间与噪声子空间划分模糊。针对该问题,本文采用Hankel 矩阵奇异值分解法对协方差矩阵进行重构。
本文对选取子频带的数据协方差矩阵R(fξ)次对角线及平行于次对角线直线上的元素进行平均处理,如式(22)所示:
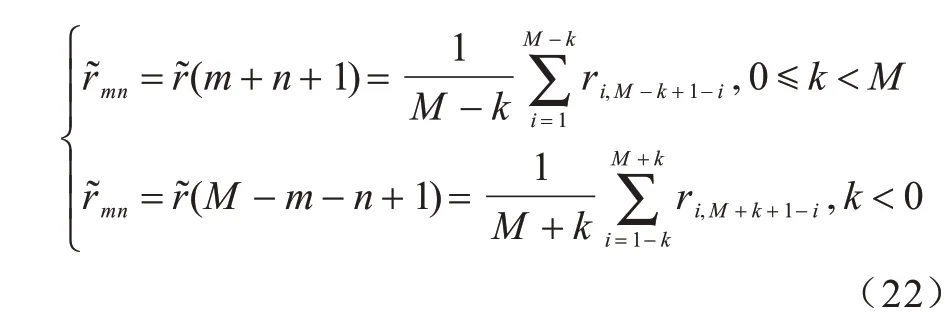
其中:k为对角线;k=0 为次对角线;0 ≤k 奇异值矩阵D中的大奇异值对应信号分量,而小奇异值对应噪声分量,因此,保留奇异值矩阵D的前P个奇异值,后M-P个奇异值为0,以实现去噪的目的,处理后的矩阵为DP。奇异值矩阵利用U、VT和DP构建新的矩阵RP(fξ),如式(25)所示: 2.2.3 信号子空间聚焦 本文对RP(fξ)及R(f0)特征进行分解,求出fξ及f0处的信号子空间Us(fξ)及Us(f0),对的乘积进行奇异值分解,如式(26)所示: 2.2.4 Root-正交传播算子 本文对协方差矩阵RMF进行分块,如式(28)所示: 其中:R1和R2分别为矩阵RMF的前P行及后M-P行,假设R1满秩,则R2为R1的线性组合,故存在(M-P)×P维变换矩阵,如式(29)所示: 其中:IM-P为M-P维单位阵。Root-正交传播算子对进行正交化,如式(33)所示: 定义多项式为: 其中:z=ejw;p(z)=[1,z,…,zM-1]T。根据式(34)计算得到P个接近于单位元上的根,对于均匀线阵,单位元上的根可通过式(35)求解: MFSS 算法的步骤主要分为:1)对阵列接收到的宽带信号数据分段,并进行离散傅里叶变换;2)选取波长间隔最接近子频带的中心频率作为参考频率,保留该子频带及其临近两条子频带;3)求得各频点处的协方差矩阵R(fξ),根据式(22)将其处理为Hankel 矩阵并利用奇异值分解重构;4)对RP(fξ)及R(f0)进行特征分解,根据各频点处的信号子空间,构造聚焦矩阵,计算聚焦协方差矩阵Rξ(f0),与R(f0)进行平均操作得到最终的协方差矩阵RMF;5)对协方差矩阵RMF分块,根据式(32)求得噪声子空间估计,计算式(35)的P个接近于单位元上的根,得到信号的DOA 估计。 为评估MFSS 算法的实用价值,本文分析MFSS、FSS、MTOPS[17]及LR-MUSIC 算法[20]的复杂度。MFSS算法的时间复杂度主要由以下5 项构成:1)选取参考频率及子频带时间复杂度O(J);2)构造协方差矩阵时间复杂度O(KM2);3)重构协方差矩阵RP时间复杂度O(M2+M3);4)聚焦获得最终协方差矩阵RMF时间复杂度O(M3);5)构造传播算子多项式求根时间复杂度O(PM2)。因此,MFSS 算法总体时间复杂度约为O(J+PM2+M3)。FSS 算法需要J个子带以实现聚焦协方差矩阵的构造,并采用MUSIC 算法构造空间谱,时间复杂度约为O(JKM2+JM3)。MTOPS算法构造协方差矩阵并特征分解的时间复杂度约为O(JKM2+JM3),计算判决矩阵的时间复杂度为O(2PM(M-P)+P2(M-P)(J-1)),求解矩阵迹时间复杂度为O(2P3(J-1)),MTOPS 算法总体时间复杂度较高。LR-MUSIC 算法构造聚焦矩阵时间复杂度为O(JM3),计算聚焦协方差矩阵时间复杂度为O(JKM2),此时的时间复杂度已接近FSS 算法,在后续计算中最优Toeplitz 矩阵通过半正定规划求出,计算量大,且总体复杂度远大于MFSS 算法。与其他算法相比,MFSS 算法在时间复杂度上具有较大优势,更利于工程应用。 本文对MFSS、FSS、MTOPS、LR-MUSIC 算法进行仿真对比,以验证MFSS 算法在短快拍情况下的有效性。假设信号源数目已知,阵元数M=8,信号为频率200~400Hz 的远场相干宽带信号,阵元间距为信号中心频率所对应的半波长,噪声为相互独立且与信号无关的高斯白噪声。DFT 点数为128,子频带数目J=20。LR-MUSIC算法是通过CVX工具包解决SDP问题。 假定2 个远场相干宽带信号入射角分别为60°和80°,快拍数为50,本文进行500 次蒙特卡洛实验。DOA 估计的均方根误差(RRMSE)如式(36)所示: 其中:C为蒙特卡洛实验的数量。 在不同信噪比时4 种算法的均方根误差对比如图3 所示,其信噪比范围从-20 dB 以间隔2 dB 升至5 dB。从图3 可以看出,在短快拍条件下,4 种算法的均方根误差均随信噪比的增加而逐渐减小。在整个信噪比范围内,MFSS 算法的均方根误差始终低于其他3 种算法。因此,在短快拍低信噪比条件下,MFSS 算法的估计误差最小。 图3 不同信噪比下4 种算法的均方根误差对比Fig.3 Root mean square error comparison among four algorithms under different SNRs 图4 不同信噪比下4 种算法估计成功率对比Fig.4 Estimation success rate comparison among four algorithms under different SNRs 本文考虑2 个入射角为θ1=60°、θ2=60°+Δθ的宽带相干信号,信噪比为5 dB,快拍数为50。若,i=1,2,则算法可以成功分辨两目标。不同角度间隔下4种算法的估计成功率如图5所示。 图5 不同角度间隔下4 种算法的估计成功率对比Fig.5 Estimation success rate comparison among four algorithms under different angular separations 从图5 可以看出,随着宽带信号源角度间隔增大,4 种算法的分辨性能明显提高,当两信号源角度间隔为5°时,MFSS 和MTOPS 算法的估计成功率达到100%,而FSS 和LR-MUSIC 算法仍无法分辨两信号源。在角度间隔小于5°时,MFSS 算法的估计成功率高于MTOPS 算法,MFSS 算法的成功估计角度间隔门限较FSS 算法降低了3°。因此,MFSS 算法在短快拍条件下能够分辨角度间隔更小的信号源。 本文考虑2 个独立宽带相干信号源的入射角为θ1=60°、θ2=80°,信噪比为5 dB。在不同快拍数下4 种算法的均方根误差对比如图6 所示。从图6 可以看出,快拍数从5 上升至50 时,MFSS 算法的均方根误差最小。 图6 不同快拍数下4 种算法的均方根误差对比Fig.6 Root mean square error comparison among four algorithms under different snapshot values 在不同快拍数下4 种算法的估计成功率对比如图7 所示。从图7 可以看出,在快拍数大于40 时,MFSS、TOPS 和LR-MUSIC 算法的估计成功率较接近,逐渐趋于1。在短快拍条件下,MFSS 算法的估计成功率始终高于其他3 种算法。因此,在同条件下,MFSS 算法具有更高的估计精度。 图7 不同快拍数下4 种算法的估计成功率对比Fig.7 Estimation success rate comparison among four algorithms under different snapshot values 本文分别考虑2 个独立宽带相干信号(入射角θ1=60°、θ2=80°)和3 个独立宽带相干信号(入射角θ1=40°、θ2=60°、θ3=80°)的情况,进行500 次蒙特卡洛实验,得出算法的平均运算时间。 不同算法的运算时间对比如表1 所示。从表1可以看出,MFSS 算法的运算时间最短,且远小于MTOPS 和LR-MUSIC 算法的运算时间。相比FSS算法,在信源数为3 时,MFSS 算法的平均运算时间降低了21.14%,更具实用性。 表1 不同算法的运算时间对比Table 1 Computation time comparison among different algorithms s 本文提出一种无需角度预估计的信号子空间聚焦算法MFSS,利用奇异值的分布规律减少快拍数及噪声对估计性能的影响,通过波长间隔与阵元间距的匹配度选取最佳参考频点及子频带,降低运算量。仿真结果表明,MFSS 算法在短快拍条件下能够有效提高估计精度。后续将提高算法在复杂噪声情况下的估计性能,使其适用于实际无线传感网络定位环境。










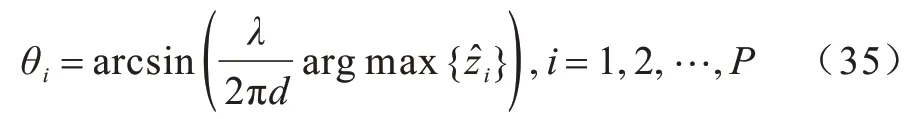
3 算法复杂度分析
4 仿真实验与分析
4.1 实验1


4.2 实验2

4.3 实验3
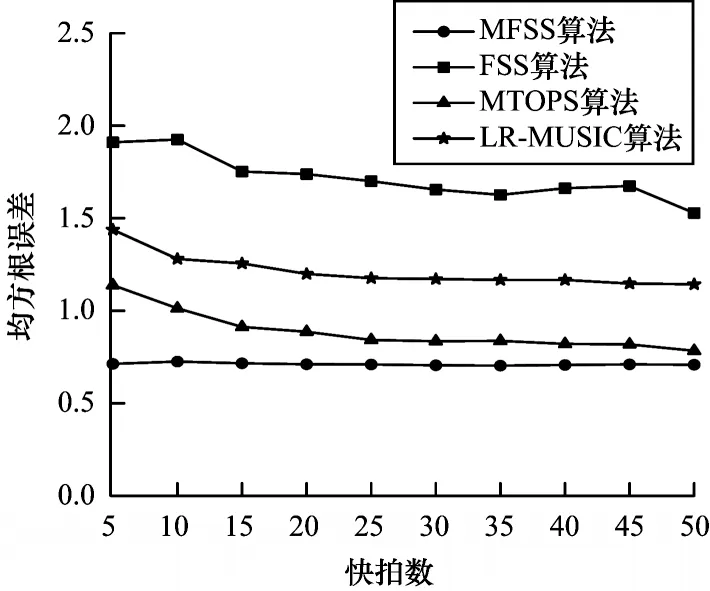
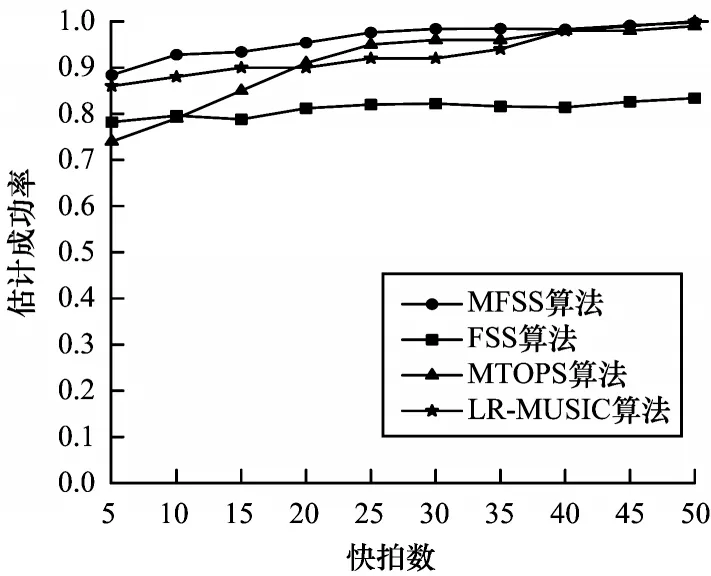
4.4 实验4

5 结束语
