往复式压缩空气系统选型计算研究
2022-01-14王华磊董志伟潘新霞李明晓姚鹏
王华磊,董志伟,潘新霞,李明晓,姚鹏
(中国石油集团济柴动力有限公司,山东 济南 250300)
1 前言
作为重要动力源之一的压缩空气,是仅次于电力的第二大动力源,因此,压缩空气使用广泛,在诸如石油化工、冶金、电力和汽车制造等行业都有压缩空气的影子,基于此,对压缩空气进行理论研究就显得尤为重要。
众所周知,空气存在于一定的空间中,但其无形无色。在一定的密闭空间内对空气施加外力,随着空气体积的减小内部压强增大。在某一瞬间,撤去外力,受空气内部压强的影响,空气会迅速恢复原有体积。这就是压缩空气的基本原理,人们利用压缩空气也是基于这一原理的。空气压缩机的实质是气源动力的提供者,是整个系统的核心,通过空气压缩机可以实现机械能与气体压力能的转换,换句话说,空气压缩机是将机械能转换为气体压力能的核心设备(图1)。

图1 空气压缩机组
压缩气缓冲罐又名压缩气稳压罐,一般存在于压缩机的出口处或用气点。将压缩空气缓冲罐设置在空气压缩机的出口处是基于以下两方面的考虑,一是可以降低出口处的压力波动,二是可以及时排出压缩冷凝水。将压缩空气缓冲罐设置在用气点是基于降低气量变化而导致的压力波动现象。
本文重点阐述工程项目压力缓冲罐容积计算选型,通过对往复式空气压缩机匹配选型的分析,得出基于工程项目的气源装置配置,使之完全满足工程应用的要求。
2 压缩气缓冲罐的计算过程推导
通常情况下,往复式压缩机缓冲罐的容积以压缩机建气流量的10%为宜,而离心式和螺杆式压缩机由于出口气压波动幅度非常小,而缓冲罐的主要作用是对冷凝水进行分析,因此,其容积根据冷凝水量予以确定。
本文不考虑分离冷凝水为主的缓冲罐,重点阐述用气点压缩空气缓冲罐容积。
在理想状态下,气体状态方程如下:
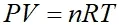
随着气体的消耗,罐内压力下降,在这种情况下对上式进行微分计算:

式中,V为气体体积;P为气体压力;R为系统空气的摩尔质量数;T为罐内温度。
罐内空气消耗与气体消耗流量之间存在以下关系:

式中,Q为气体消耗流量;t为耗气时间。
将(2)式代入(1)式中得。

根据以上(1)、(2)、(3)式分别对气体体积和耗气时间进行分析:
气体体积、耗气时间和压力之间的关系:
由(2)式可知:

dn/dt:耗气摩尔流量;
假设工程中设备耗气量为S(Nm3/min),
标准大气压力P0=101325Pa;
由(4)变形:
Dn/dt=P0S/RT
由此得出下式:

对(5)式积分得:

式中,P1为供气起始压力;P2为供气终止压力。
由(6)变形后:

式中,V为气体体积m3;τ为耗气时间min;S为设备耗气量Nm3/min。
标准大气压力P0=101325Pa。
3 案例分析
3.1 缓冲罐选型案例分析
以某项目为例,该项目的压缩机可以持续产生6~8kg的压缩气,马达启动耗气量695L/S,每次启动历时6~8S。如果使其启动时间固定为8S,则马达工作压力需要6~8bar。
统一单位后,S=41.7Nm3/min;τ=0.14min;P1=8bar;P2=6bar;
根据以上公式可以得出在标准状况下,气体的体积为2.8方,工作压力为0.47方。进一步计算出需要的缓冲罐应为0.5m3。
3.2 压缩机及储罐选型分析
通常情况下,压缩气的气源系统需要单独设置,且要求其能够连续启动6次。同时,在检测到储罐内压力达到某值时,压缩机可以自动续压到设计要求。
根据上述数据,储罐设计压力确定为3MPa,则储罐压力降到2MPa时,压缩机开始续压,续压历时时间为20min。根据以上情况,设置相应的储罐和压缩机。
在马达满足连续启动6次的情况下,耗气量为33.36Nm3,所需时间为0.8min,压差达到10bar。在标准状况下,气体体积为2.67Nm3。实际工作中,压力一直维持在10bar以上,此时,估算出压力为0.3方。
系数为1.5的情况下,储罐按照0.5m3予以配置。
通过(6)式计算压缩机的出力能力,在压力恢复时间为20min的情况下,得出:
τ=V(P1-P2)/P0ΔS
τ=20min;V=3Nm3;
P1-P2=10bar;
ΔS为压缩机的泵气流量减去消耗气量;
通过计算得出,ΔS为1.5m3/min;在3MPa状态下,马达的启动需要耗气1.39m3/min,但值得强调的是,通常情况下,压缩机在启动阶段时,启动马达处于非工作状态。
可配置压缩机的泵气流量为:1.5m3/min,压力是3MPa。
4 仿真模拟验证
在工程界,使用较广泛的软件之一是Matlab,因此,本文在模拟仿真压缩空气系统的时候使用该软件,从而计算出以上公式是否科学。
在列出有关方程式的基础上,按照质量守恒、能量守恒等方程,基于温度、压力两个时间变化量进行分析。基于此,本次涉及的变化参数主要有三个,即m、T和P。
质量守恒方程
Dm/dt=M_in-M_out
能量守恒方程
Udm/dt+mC_vdT/dt=M_inh_in-M_outh_out
整理后:
dT/dt=(Minhin-udm/dt-M_outh_out)/(mC_v)
理想气体状态方程
RT/Vdm/dt+p/TdT/dt-dP/dt=0
整理后:
dP/dt=RT/Vdm/dt+p/TdT/dt
接下来,在MATLAB/Simulink软件中根据所列数学模型方程搭建仿真模型如图2。
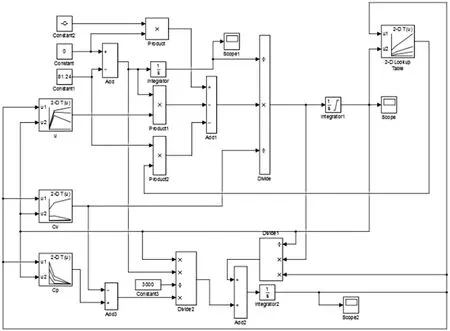
图2
最后,对上述三种实例情况进行模拟:
(1)缓冲罐选型案例模型分析如图3。
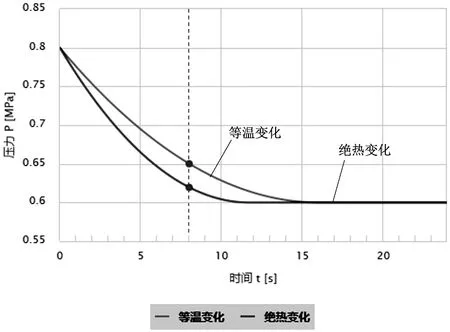
图3
0.5m3缓冲罐可以满足一次启动(8S)瞬态耗气过程中的压力要求。
(2)压缩机及储罐选型案例模型分析如图4。
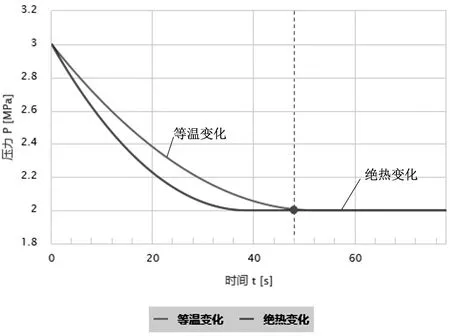
图4
0.5m3储气罐可以满足6次启动(48S)耗气过程中的储气压力从3MPa降低到1.2MPa要求。 1.5m3/min产气量的空气压缩机满足20min(1200S)内将储罐压力从2MPa达到3MPa的要求(如图5)。
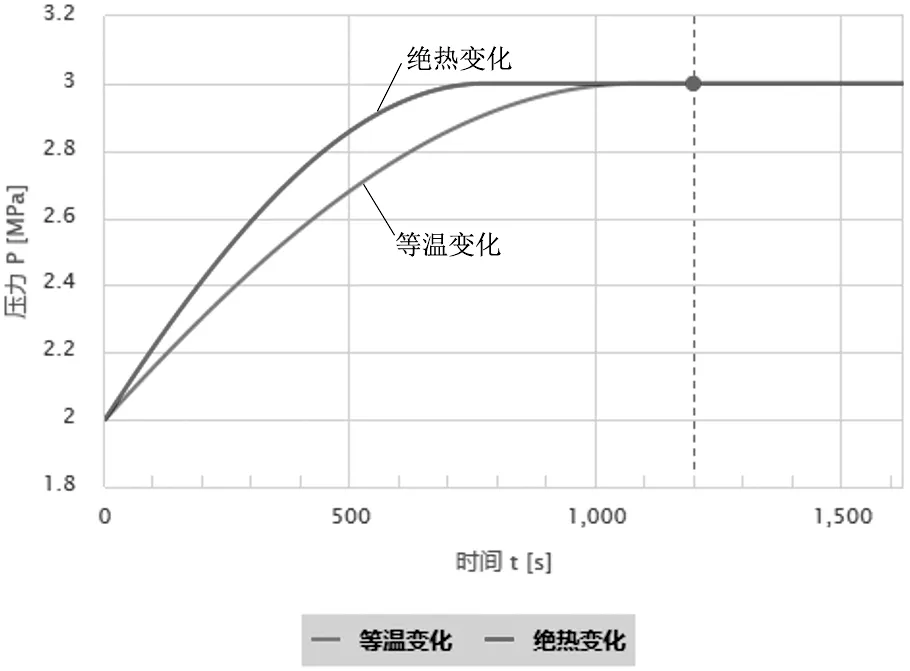
图5
5 结语
本文从理论上对缓冲罐容积计算选型进行了分析,在此过程中引入有关公式进行了推导。同时,以实际案例分析为导向,分别对低压气源和自备压缩气源两种型号的储气罐和缓冲罐及压缩机进行了计算配置选型。在选型计算过程中,重点考虑压缩机气源系统续压时间等问题。通过有关软件进行模型推导和仿真,对结果进行了验证分析。
根据以上分析可知,此类选型计算可以在类似气体输送系统中进行应用,因此,具有较强的理论意义和现实意义。
