采用优化PID控制的电液执行器跟踪仿真研究 ①
2022-01-14赵新华杨思国
赵新华, 杨思国
(滁州职业技术学院 电气工程学院,安徽 滁州 239000)
0 引 言
电液执行器包含电气和机械两大部分,具有响应速度快、控制精度高和输出功率大等优点,广泛应用于机床、机械手、汽车和挖掘机等领域[1-2]。随着社会的发展,工业上对电液执行器也提出了更高的要求。要求电液执行器响应速度更快,输出精度更高。但是,在现实应用中,电液执行器由于摩擦、扭转等各种因素,导致控制精度不太理想。达不到设备的期望值,完成不了工业中高精度的要求任务,有些状况下,甚至造成整个工程建设出现重大的经济损失。因此,加快电液执行器控制系统的稳定性研究,才能改变落后局面。这不仅可以提高我国自主研发的能力,还能提高国产电液执行器在市场中的竞争力。
目前,为了改善电液执行器控制系统的稳定性,大量学者对电液执行器控制系统展开了广泛的研究。例如:文献[3-4]研究了电液伺服系统模糊PID复合控制方法,分析了比例阀中的死区位置,根据模糊规则和理论,设计了模糊PID控制方法,搭建仿真平台进行验证,提高了控制系统位移信号的响应速度和跟踪精度。文献[5-6]研究了电液系统滑模控制方法,建立电液比例阀数学模型,定义了控制状态参数变量,设计了液压系统的滑模控制器,搭建液压系统仿真模型进行位置跟踪验证,比较不同控制方法输出误差曲线,提高了电液系统位置信号跟踪精度。文献[7-8]研究了电液伺服阀神经网络PID控制方法,创建其驱动简图,推导出伺服阀驱动动力学方程式,利用神经网络对PID控制器进行优化,通过神经网络算法进行误差逼近,提高了执行器位置信号跟踪精度。但是,在面对复杂工况条件下,很难做出快速反应,导致电液执行器控制精度下降,不能很好的适应多变环境。
1 电液执行器
电液执行器驱动结构如图1所示。当马达M驱动泵时,油从油箱流向液压回路。带有内部反馈的比例阀PV控制系统流量。有四个切断阀SV1至SV4,一次只有两个保持打开状态。结果,活塞的运动在图1所示的两个水平安装的气缸中实现。标记为S的表示单杆类型,标记为D的表示双杆类型。弹簧用于加载活塞。线性可变差动变压器(LVDT)提供活塞位移的控制反馈。设置中使用的单级安全阀RV将泵压力保持在极限附近的合理恒定水平。当电磁阀接收到来自与实时系统RTS接口的阀控制卡VCC的放大电压e时,在PV中施加滑阀运动的力由电磁阀实现。它有一个实时处理器、一个输入模块IM和一个输出模块OM。当OM向VCC发送命令电压时,IM接收与测量位移yL对应的LVDT信号。Labview软件用于在主机PC上开发控制器,然后将其加载到实时处理器上。
在控制器中,定义总电压[9]为式(1)-(3):
e=ef+eb
(1)
(2)
ye=yd-yL
(3)
式(1)-(3)中:ef为前馈电压;eb为反馈电压;ye为位移误差;kp为比例增益系数;ki为积分增益系数;kd为微分增益系数;yd为期望位移;yL为实际位移。

图1 电液执行器驱动装置
反馈控制器具有相对较弱的非线性特性。这种非线性以阀门摩擦或油的可压缩性的形式出现在系统中。通常采用前馈控制器来补偿强非线性,如计量端口的压力变化和气缸中的摩擦。这两者都取决于所需的活塞速度为式(4):
(4)
活塞的摩擦力定义为式(5),(6):
Ff=F0,|v|≤v0
(5)
Ff=Fc+(Fb-Fc)exp{-(vd-vb)2
/(vs-vb)2}+αv(vd-v0),|v|>v0
(6)
式(5),(6)中:F0为粘滞力;v0为滑移速度;Fc为库仑摩擦力;vs为斯特里贝克速度;αv为粘性摩擦系数;Fb为最大边界润滑摩擦力;vb为相对速度。
活塞期望加速度为式(7):
(7)
式(7)中:ks和ma分别为弹簧刚度和驱动质量。
活塞伸展运动过程中,前馈电压信号为式(8):
(maad+αvvd+ksyd+F0)]}e0/2
(8)
2 控制器优化
2.1 PID控制器
在工业自动化控制系统中,PID控制系统应用领域相对广泛。电液伺服系统采用PID 控制方式,如图2所示。
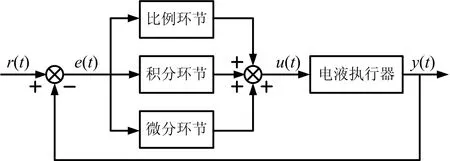
图2 电液执行器PID控制
当前,PID控制器大多采用增量式[10-11]控制形式,其表达式为式(9):
(9)
式(9)中:t为时间;u(t)为控制信号;Ti为积分时间常数;Td为微分时间常数。
采用增量式PID控制器,其输出误差定义为式(10):
e(t)=r(t)-y(t)
(10)
式(10)中:r(t)为输入信号;y(t)为输出信号;e(t)为误差信号。
2.2 优化PID控制
采用遗传算法对PID控制器进行优化,遗传算法主要分为以下几个步骤:
1)染色体编码和解码,采用二进制方式对染色体进行编码和解码。
2)初始种群生成,随机生成N个样本,进行全局搜索,设置当前迭代次数t和最大迭代次数T。
3)个体适应度函数判断,使控制系统输出误差最小,适应度函数定义[12-13]为式(11):
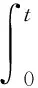
(11)
4)寻优操作,通过选择、变异和交叉操作,淘汰劣质个体,保留优秀个体。
5)终止条件的判断,如果t≤T,继续搜索,若t>T,停止搜索,保留搜索的最优值。采用遗传算法对电液执行器控制器进行优化,优化过程如图3所示。

图3 PID控制优化流程
3 误差仿真
采用遗传算法优化PID控制器,其控制性能到底如何,接下来,通过MATLAB软件对电液执行器输出误差进行仿真,并且与优化前PID控制性能进行对比。初始参数设置为:种群大小为50,PID控制器参数取值为kp=30,ki=0.2,kd=1,交叉概率取值为Pc=0.6,变异概率取值为Pm=0.02,容许最大迭代次数取值为T=150。
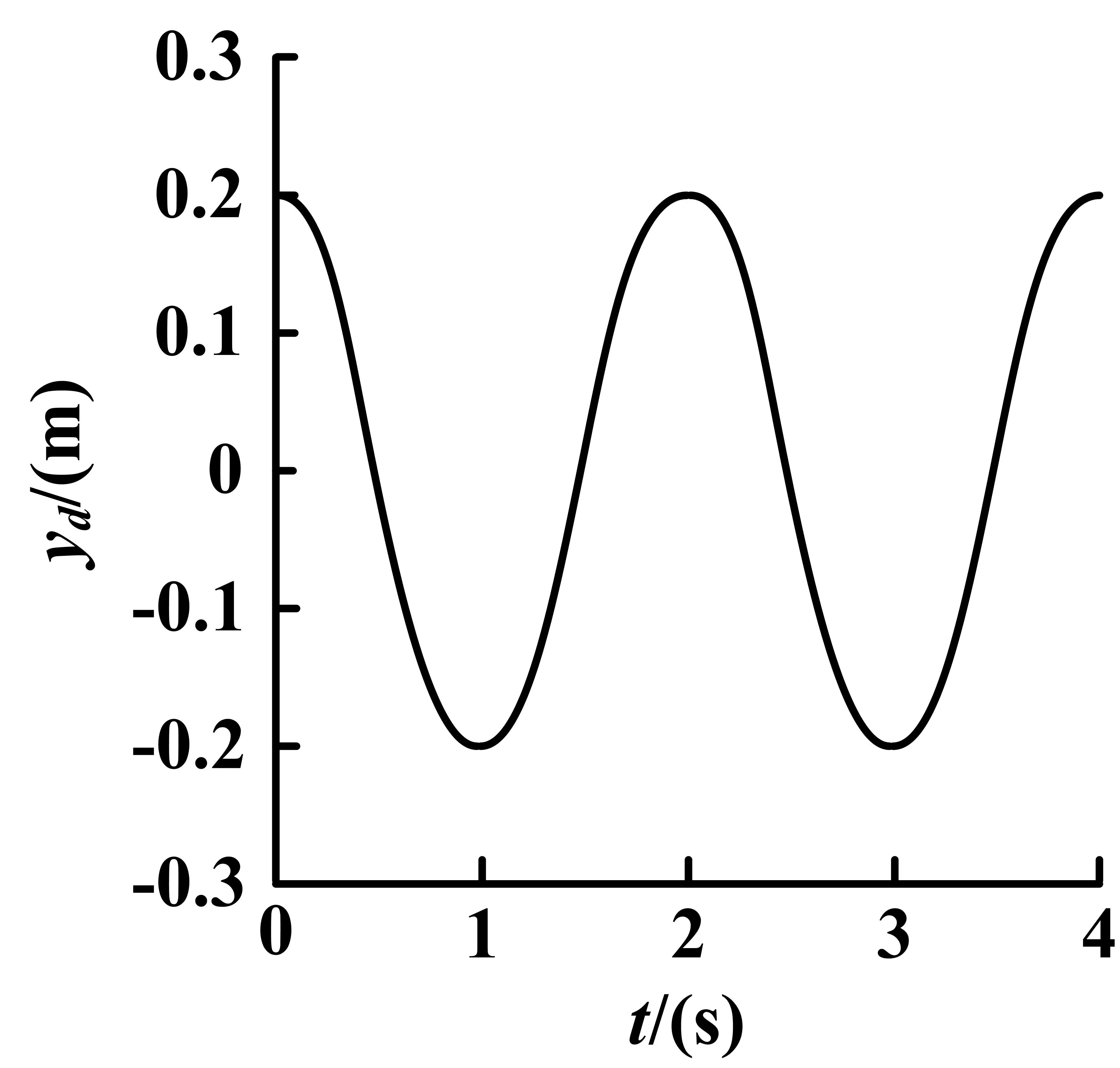
图4 电液执行器期望位移
假设电液执行器期望位移信号为余弦弦信号,如图4所示,干扰信号为正弦波(τ=sinπt)。采用PID控制器,电液执行器跟踪误差如图4所示。采用遗传算法优化PID控制器,电液执行器跟踪误差如图5所示。
分析图5误差变化曲线,电液执行器0.5s后处于稳态误差,整个阶段的输出误差变化幅度较大,在波峰和波谷处产生的误差更大,不能适应波峰和波谷信号的跟踪,自适应调节能力较差,面对外界干扰,导致稳定性下降。分析图6误差变化曲线,电液执行器0.2s后处于稳态误差,整个阶段,输出误差变化幅度较小,在波峰和波谷处仍然能够保持较好的跟踪效果,自适应调节能力较强,面对外界干扰,能够产生抑制作用,使控制系统保持在良好状态。因此,采用遗传算法优化PID控制器,能够提高电液执行器开始跟踪的反应速度和整个阶段的跟踪精度,抗干扰能力特别强,稳定性较好,特别适合高精度电液执行器的控制系统。

图5 PID控制跟踪误差

图6 优化PID控制跟踪误差
4 结 论
针对电液执行器运动位移跟踪精度较低、抗干扰能力较差等问题,设计了优化PID控制的电液执行器控制系统,通过仿真检验控制系统的稳定性,主要结论如下:
(1) 采用PID控制方法,电液执行器位移信号跟踪效果较差,容易受到复杂环境的干扰,导致控制系统反应速度较慢,输出误差较大。
(2) 采用遗传算法优化PID控制方法,电液执行器位移信号跟踪效果较好,抗干扰能力强,控制系统反应速度较快,输出误差较小,更适应复杂环境位移信号的跟踪。
(3)采用遗传算法对控制系统进行优化,能够调整控制系统由于不确定性造成的异常,保证目标跟踪的精确性和鲁棒性,对提高电液执行器的稳定性具有重要的意义。
