基于GRACE数据的长江流域地表水储量变化
2022-01-13叶勤玉李小龙金涛勇何泽能杨世琦
叶勤玉,张 强,李小龙,金涛勇,何泽能,杨世琦
(1.重庆市气象科学研究所,重庆 401147;2.重庆市气象局,重庆 401147;3.武汉大学测绘学院,湖北 武汉 430072)
0 引言
陆地水储量是水文循环的关键一环,是评估区域水量收支状态的重要参数。目前对陆地水储量变化的监测方法主要有:站点观测法[1]、卫星遥感反演法[2-3]、物理模型模拟法[4]、GRACE重力卫星反演法[5]。站点观测法受实际地形地貌的影响,很难对大尺度区域进行测量;卫星遥感反演方法只能反演表层土壤水分,不能对深层水进行探测;而物理模型模拟方法中观测站点的分布不均影响了其精度和应用范围。GRACE重力卫星具有全球观测尺度统一、分布均匀等优势,被广泛的应用于全球以及区域尺度的陆地水储量变化监测评估中[6]。
近年来,利用GRACE重力卫星数据研究陆地水储量变化特征备受研究者的关注。冯贵平等[7]利用GRACE重力卫星数据反演了2002年4月—2011年2月的月间隔全球陆地水总储存量,并分析了其季节性和长期变化特征。结果表明,GRACE反演的全球地下水储量具有明显的季节性变化和长期趋势。尼胜楠等[8]利用GRACE数据反演长江、黄河流域的水储量变化,并与水文模型进行对比,研究其季节性和年际变化特征。结果表明,GRACE反演水储量季节变化振幅略大于水文模型,可揭示厘米级等效水高变化。刘任莉等[9]利用GRACE卫星数据反演了2003—2010年中国陆地水储量变化,结果表明,GRACE反演的陆地水储量变化结果与基于实测水文、气象数据的结果符合较好,对2009—2010年西南五省特大旱灾也有着较好的反映。徐永明等[10]利用GRACE RL06数据及GLDAS数据对云贵高原陆地、地表以及地下水储量变化进行了反演,并对水储量变化时序进行了特征分析。结果表明,2002—2010年,GRACE与GLDAS反演的陆地水储量的相关系数达0.94,且两者的变化趋势一致。魏光辉等[11]对GRACE估算的陆地水储量进行降尺度,分析了2002—2015年间塔里木河流域局部的干旱特征。结果表明,流域内GRACE陆地水储量与GLDAS土壤水的相关系数达0.35。陈智伟等[12]反演了2005—2012年珠江流域的陆地水储量变化,结果表明,ITSG-GRACE 2018模型反演的珠江流域陆地水储量季节性变化特征与GLDAS水文模型、降水数据以及地下水测井监测数据具有较好的一致性。丁一航等[13]利用GRACE研究发现我国四大流域水储量变化信号具有多种周期特性,研究结果与GLDAS结果具有很强的相关性。曹艳萍等[14]利用GRACE重力卫星反演河南省水储量变化,发现河南省陆地水储量变化呈现典型的“余弦曲线”分布特征。
长江流域是我国面积最大、水量最丰富的流域,同时也是我国人口密度最大的区域之一[15]。研究长江流域的水储量变化对探究流域水储量变化特征、分析不同水文地质条件对水储量变化影响、指导自然资源的合理开发和生产活动顺利进行、维护和保障国家安全有着重要的战略意义。本研究利用2002年4月—2017年6月的GRACE数据,反演了长江流域的水储量变化,以期为长江流域水资源合理利用与配置提供参考。
1 研究区与数据
1.1 研究区域
长江是我国最长的河流,发源于青藏高原,自西向东流经青海、西藏、四川、云南、重庆、湖北、湖南、江西、安徽、江苏、上海等11个省市,并最终注入东海。长江流域,是指长江干流和支流流经的区域,是世界第三大流域,流域总面积约180万 km2,维护和保障了我国的生态安全、供水安全、粮食安全、能源安全[16]。受西太平洋副热带高压的强度以及位置的影响[17],长江流域年降雨量与暴雨时空分布不均,年降雨量约1 100 mm,水储量变化具有很强的周期性[18]。

图1 研究区高程图Fig.1 DEM of Yangtze River Basin
1.2 数据
GRACE(Gravity Recovery and Climate Experiment)卫星由美国国家航空航天局(NASA)和德国航空航天中心(DLR)联合研制,于2002年3月发射成功,旨在提供高精度、高分辨率的地球重力场静态分布数据,监测月尺度上地球重力场的时空变化特征。GRACE数据由德州大学空间研究中心(CSR)、德国地学中心(GFZ)和喷气推进实验室(JPL)3家机构处理并发布,数据形式为月重力场球谐系数,经过相应的反演程序即可获取区域质量变化信息。除球谐系数外,3家机构还同时发布了Mascon产品,该产品为进行适当空间平滑后的全球格网点重力异常,可以用来进行后续验证和进一步对比分析。
本文选择的GRACE数据为CSR于2018年6月发布的球谐系数产品,版本为最新的RL06,数据类型为GSM。RL06版本可以提供最大阶数为96阶和60阶的两组月重力场模型,而GSM表示扣除了高频海洋信号和非潮汐因素等的影响,产品时间跨度为2002年4月—2017年6月。
为了对GRACE反演结果进行验证,我们选择了3种气象数据模型:降雨模型选择TRMM 3B43 v7数据集。该数据空间分辨率0.25°×0.25°,时间分辨率为1月,观测范围为50°S~50°N,180°W~180°E,覆盖包括长江流域在内的我国大部分区域,时间跨度为2002年1月—2018年12月;径流数据选择水文站实测数据,包括大通站、宜昌站等,时间跨度为2000年1月—2020年10月;蒸散模型选择ESA于2019年5月发布的GLEAM v3.3a全球蒸散数据集,该模型的时间跨度为1980—2018年共39 a,模型时间分辨率为月,空间分辨率为0.5°×0.5°。所有要素的时间间隔统一为2002年4月—2017年6月。表1为数据信息汇总表。

表1 数据信息汇总表Tab.1 Data information table
2 地表水储量反演与验证方法
地球重力场通常可以用大地水准面的形状来描述,地球上某一点的大地水准面N可以表示为一组球谐系数的总和[19]:
(1)

(2)
大地水准面的变化会导致地表密度的重新分布,记密度变化为△ρ(r,θ,λ),球谐系数的变化可表示为:
(3)
其中,ρavs为地球平均密度,数值为5 517 kg·m-3。不妨假设△ρ为一厚度为H的薄层,并设地球表面面密度变化为△σ,则可以将其表示为△ρ的积分:
(4)


(5)
公式(5)反映了地表质量变化对大地水准面的影响,而在地表物质迁移的同时,作为滞弹性体的地球也会在表面负荷变化的作用下产生形变,并引起大地水准面的变化,即[20]:
(6)
其中kl为l阶负荷勒夫数,表征滞弹性体对表面负荷的形变响应。综合公式(5)、(6),大地水准面的总变化为:
(7)
将面密度变化△σ展开:
(8)
其中ρw表示水的密度,数值为1 000 kg·m-3,△lm、△Ŝlm为无量纲规格化球谐系数。根据公式(8),有:
(9)
联立公式(5)、(6)、(7)、(9)可得:
(10)
联立公式(2)、(10)得:
(△Clmcos(mλ)+△Slmsin(mλ))
(11)
在陆地水储量变化分析中,通常使用等效水高EWH(Equivalent Water Height)来表示地表质量的变化,△EWH和△σ有如下关系:
(12)
联立公式(11)、(12),有:
(13)
其中ρave为地球平均密度,其数值为5 517 kg·m-3,ρw表示水的密度,数值为1000 kg·m-3。
GRACE发布的数据反映了地球静态重力场,动态变化信息会被大量静态信号淹没,因此需要将背景场去除掉,以放大时变信号,通常选择2004—2009年的平均值作为背景场,并从每月球谐系数中扣除[21]。注意到GRACE卫星轨道中心为地球的瞬心,因此与地球质心有关的C10、C11、S113项无法反映真实的重力场信号;同时GRACE卫星轨道近圆,对反映地球扁率的C20项也不敏感。因此,在利用GRACE数据反演地表质量变化前,需要对以上数据进行替换,通常选择基于海洋模型的一阶项系数和基于卫星激光测距SLR(Satellite Laser Ranging)的C20项系数作为替代[22-23]。
同时,在反演过程中,需要将系数进行截断以降低噪声,但这种方法并不能将噪声清除干净,这是因为此时的球谐系数除仍存在着高频噪声和南北方向上的条带误差。这些误差有两种来源:一是GRACE重力场模型高阶位系数中存在着较大的随机误差,需要用高斯滤波进行去除,通常选择300 km高斯滤波[24];二是相同次数、不同阶数的系数之间存在着相关关系,在空间域上表现为南北方向出现的明显条带,需要通过于PxMy模型方法进行降噪,通常选择P3M9法[25]。上述两种滤波方法虽然能较大程度上去除噪声,但同时也带来了新的误差:泄露误差,这是一种伴随着信号截断和空间平滑出现的误差,需要使用基于尺度因子法的泄露误差改正方法进行改正[26]。
冰后回弹效应PGR(Post Glacial Rebound),又称冰川均衡调整GIA(Glacial Isostatic Adjustment),揭示了始于7万年前、终于1.15万年前的末次冰期对黏弹性地球的影响。在末次冰期,地球上绝大部分区域都被大冰原覆盖,地表在冰原巨大的重力作用下不断凹陷;1.8万年前冰川开始消退,大片冰原消融,但由于地幔的黏弹性,原来负载冰盖的地区会在压力减小后向上弹起,对地壳运动、重力场反演、地表质量迁移等都有着重要的影响。本文使用基于最新的GIA模型——A13模型的冰川均衡调整方法[27]。
在获取指定区域地表水储量变化TWSC(Terrestial Water Storage Change)时间序列后,需要对序列进行频谱分析以得到该区域水储量变化的频谱域特征,包括趋势项、季节项、异常项等信号。因此本文选用基于最小二乘的水储量变化时间序列分析方法[28],可由以下函数模型近似表达:
(14)
式中,a0为拟合残差,a1为趋势值,fi(i=1,2)为信号频率,单位为1/a,φi为信号相位。当i=1时对应周年信号,此时fi=1,bi为周年信号振幅;当i=2时对应半周年信号,此时fi=2,bi、ci为半周年信号振幅。
基于GRACE卫星的水储量变化反演及分析流程如图2所示:①系数替换。将2004—2009年的系数平均值作为背景场,并从每月球谐系数中扣除;②使用海洋模型和SLR数据对一阶项和C20系数进行替换;③对重力场模型进行300 km高斯滤波和P3M9去相关滤波,得到基本消除高阶误差和南北条带的质量变化空间分布;④利用尺度因子法对泄露误差进行改正,恢复被信号截断和高斯滤波污染的信号;⑤利用A13模型消除冰后回弹效应的影响;⑥利用最小二乘法对获得的地表水储量变化时间序列进行分析和处理,从而得到序列的趋势、周年信号、半周年信号等重要参数,并分析它们的时空变化特征。
为验证水储量变化结果的准确性,采用水文要素模型对GRACE结果进行评估。基于流域水量平衡方程,区域水储量变化与降雨(P)、径流(R)、蒸散(ET)之间存在着如下关系:
△TWSC=P-ET-R
(15)
因此,在获取气象要素时间序列和空间分布后,可以拟合水储量变化的时空规律,拟合效果越好,就说明GRACE结果越精确。同时,由于长江流域位于东亚季风带上,降雨变化和后续的径流蒸散过程是导致其水储量变化的主要影响因素,因此对气象要素的研究有助于了解水储量变化的主要驱动力和驱动过程,有助于评估流域尺度的水量收支状态。
3 结果与分析
3.1 长江流域水储量时间变化特征分析
时间变化特征即为时间序列的趋势,周年、半周年项的振幅以及相位等信息。使用基于最小二乘的水储量变化时间序列分析方法,对时间序列进行频谱分析,获取序列趋势项、季节项等变化特征。

图2 地表水储量变化反演与分析流程Fig.2 Flow chart of terrestrial water storage changes inversion and analysis
长江流域2002年4月—2017年6月的地表水储量变化时间序列及其最大影响源:降雨的时间序列对比见图3,特征分析结果如表2所示[29]。

图3 长江流域2002年4月—2017年6月地表水储量变化与降雨时间序列对比Fig.3 The time series terrestrial water storage changes in the Yangtze River Basin from April 2002 to June 2017
结合表2,从趋势项可以推断2002年4月—2017年6月这16 a间,长江流域整体水储量处在一个缓慢上升的状态,长江流域水储量变化速率为4.1±1.1 mm·ɑ-1,总体水量在此期间增加了大约1.1×1011T,说明长江流域在近16 a来处于丰水状态,平均每年增加约1.6个太湖的水量。

表2 长江流域2002年4月—2017年6月地表水储量变化与降雨时间序列特征分析表Tab.2 The characteristics of the time series terrestrial water storage changes and precipitation in the angtze River Basin from April 2002 to June 2017
考虑到长江流域复杂的地质构造、特殊地形以及人为因素的影响,长江流域水储量变化的周期信号有很多,最主要的是周年信号和半周年信号。表2的结果表明,长江流域地表水储量变化中有着56.0 mm等效水柱高的周年性波动,半周年波动的振幅为10.9 mm等效水柱高;而降雨的周年振幅是地表水储量周年振幅的约1.5倍,半周年振幅则与地表水储量相当,相关系数高达0.75,反映了降雨对长江流域地表水储量变化的深刻影响。地表水储量变化的周年相位约-6.6°,且振幅为负,揭示了长江流域水储量在每年8月左右达到最大值,在2月左右达到最小值,这与实际情况相吻合。长江流域受亚热带季风气候的影响,夏汛集中在5—8月,降雨的增加会导致水储量的大幅度增加,于是在8月左右出现峰值;而汛期过后,水储量逐渐平稳,随着秋冬季节的到来,降水减少,加之大量蒸散发作用,水储量逐渐减少,并在2月左右出现谷值,这一变化规律同样体现在降雨序列中。降雨周年项的相位为-0.1°,表明降雨在每年的7月达到峰值,并在1月达到谷值,这一结果与水储量之间存在着约1个月的间隔,这是因为降雨是一个动态过程,且降雨除了蓄积在流域内,还有部分以径流、水蒸气的形式流出,所以降雨过程结束后需要一段时间才能在水储量中有所体现。
长江流域地表水储量半周年相位为-6.6°,振幅为10.9 mm,说明长江流域水储量除了“2月谷值—8月峰值—2月谷值”这种水储量周期变化模式外,还存在着“2月峰值—5月谷值—8月峰值—11月谷值—2月峰值”的变化规律,且规模只有前者的20%左右;而降雨的半周年相位为0.2°,揭示了降雨“12月峰值—3月谷值—6月峰值—9月谷值—12月峰值”的变化规律,与水储量变化之间存在2个月的时延,与周年项的1个月不同,推测可能是因为振幅较小,所以需要累积更长时间才能被GRACE卫星捕捉到,而降雨的半周年振幅为10.1 mm,几乎与水储量变化振幅相同。
3.2 长江流域水储量空间变化特征分析
空间分布特征体现了区域内不同格网点、不同参数的分布特征和规律。图4a、4b分别为长江流域2002年4月—2017年6月1°×1°格网点上地表水储量变化趋势项、周年项振幅绝对值的空间分布,可以分辨出长江流域上各格网点、各区域、各水系的水储量变化分布特征。
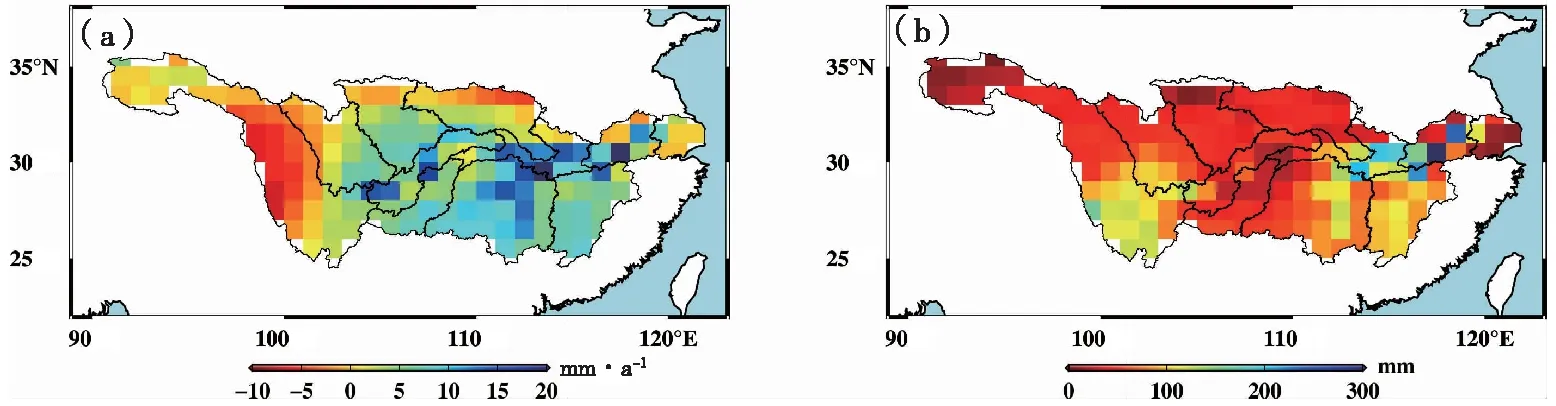
图4 长江流域2002年4月—2017年6月地表水储量变化的趋势(a)和周年项振幅绝对值(b)空间分布Fig.4 Trends and absolute values of annual signals’ amplitudes of water storage change in the Yangtze River Basin from April 2002 to June 2017
总的来看,长江流域大部分区域水储量在2002年4月—2017年6月间保持着增加的趋势,且在中下游区域增速较快,而金沙江流域中部大片区域以及岷江流域、嘉陵江流域、汉江流域北部等区域的水储量处在持续减少的状态。年际信号的振幅反映了水储量周期变化的幅度,可以看到长江流域周年振幅较为平稳,统计后发现全流域平均振幅为64.9 mm,78.4%的格网振幅均小于100 mm,而在金沙江流域南部以及洞庭湖流域东部、鄱阳湖流域等中下游区域振幅较大,部分地区达到200 mm以上。
3.3 水储量变化的水文气象验证
为了验证GRACE水储量变化结果的准确性,基于流域水量平衡方程,我们选择长江流域上游2007—2016这10 a间的水储量和水文气象数据,探究GRACE卫星在流域尺度的观测效果和适应性,同时分析水储量变化的驱动因素。图5为长江流域上游水储量变化和降雨—蒸散—径流的时间序列对比,发现二者的变化规律十分接近。2006—2016年,长江流域上游水量收支状态基本平衡,即水储量的变化量(-3.7 mm·a-1)≈输入量(降雨0.4 mm·a-1)-输出量(蒸散0.1 mm·a-1+径流3.8 mm·a-1),同时收支状态基本平衡也反映出这些水文要素模型的准确性,它们在长江流域上游的这10 a间有着很好的拟合效果,总体上呈现出良好的评估效果。

图5 长江流域上游2007年1月—2016年12月水量收支状态Fig.5 The water storage changes of upper Yangtze River from January 2007 to December 2016
4 结论
本文利用GRACE重力卫星数据对长江流域地表水储量变化进行了分析。结果表明:2002年4月—2017年6月近16 a间,长江流域整体水储量处在一个缓慢上升的状态,地表水储量变化速率为4.1±1.1 mm·ɑ-1,总体水量在这一期间增加了大约1.1×1011T。在长江中下游区域,水储量增速较快,而金沙江流域中部大片区域以及岷江流域、嘉陵江流域、汉江流域北部等区域的水储量处在持续减少的状态;流域大部分区域水储量的年际波动较为平缓,78.4%的格网振幅均小于100 mm。降雨对长江流域水储量变化周期项的影响程度较大。基于水文气象数据的统计分析显示这一结果能够较为准确的体现长江流域近16 a的水量收支状态。
目前GRACE卫星任务已结束,后续卫星GRACE Follow-On已发射,但数据尚未发布。未来将继续关注GRACE Follow-On卫星数据,对长江流域地表水储量变化进行更加详细和深入的研究与分析,并研究与GRACE卫星空间时间段数据的填补问题,实现对长江流域陆地水储量的长期监测。
