杨氏双缝实验中的干涉与衍射现象

白旭峰，杨艳丽，曲保平

晋中信息学院，山西 晋中 030800

0 引言

光的干涉与衍射是光学中非常重要的一部分内容，是现代光学的基础，为变换光学、全身照相等现代技术的发展与应用提供了强有力的理论基础[1]。但与此同时，它也是教学过程中的重点与难点，在普通物理学中，光的干涉与衍射会作为独立章节展开讲解，这样很容易导致学生无法全面理解概念[2]。杨氏双缝干涉、单缝衍射实验是物理光学中较为经典的实验，能够将干涉与衍射相关知识点联系起来，从而帮助相关人员更好地理解并掌握这一方面的全部内容[3]。

1 光的干涉和衍射现象的联系与区别

了解当前国内外各个大学的物理教材可以发现，关于双缝、单缝、光栅等实验相互联系并进行更深层次探究的内容很少。在我国，绝大部分教材都是单独介绍双缝干涉与单缝衍射实验，而作为高校物理教师，在理解干涉的明暗分布时会更加注重光程差的角度分析，在探究衍射图样特点时则会应用半波带法。两者的区别主要体现在纯衍射实验和纯干涉实验中，前者指的是当缝宽较大时，每个狭缝中散发出的光波具有明显不相等的振幅，可以理解为无限个连续次波的相干叠加效果，这是常见的单缝衍射，即纯衍射实验效应[4]；后者指的是当缝宽较小时，每个狭缝可以看作只有一个线光源，无法再继续等分，这时便无须考虑同一光束的次波叠加，只需要考虑两个缝之间是否有相互间波的相干叠加即可，这是纯干涉实验效应[5]。

虽然纯衍射实验和纯干涉实验两者有十分明显的区别，但这并不意味着两者完全对立，相反，可以将其看作是一个相同的光学现象。其原理都是波场相干叠加，且在图样上都是明暗相间的条纹状，不同的是干涉现象中条纹长度及宽度基本相同，而衍射则宽度、亮度均不相同，中央最宽且最亮。

2 杨氏双缝实验

2.1 双缝干涉实验

如图1所示，设相干光源S1、S2之间的距离为d，中点M到屏幕E的距离为D，P为任意一点，令P到S1、S2之间的距离为r1、r2，此时从S1、S2所发出的光到达P点的光程差δ=r2-r1。如果设P点到对称中心O点的距离为x，PM与MO之间的夹角为θ，则一般情况下D＞d，D＞x，也就是说θ角很小，sinθ≈tgθ，故。

图1 杨氏双缝实验干涉条纹计算图

即图2中的曲线a。由此可得，当δ=±0,1,2,…时，光（k=0,1,2,…）时，光强I=0，即暗条纹的最暗处。从能量观点的角度分析，干涉现象使得光重新进行了分布，但仍旧遵循光的能量守恒。强I=4I0，即明条纹的最亮处；当

图2 双缝干涉、单缝衍射、双缝衍射实验中的光强度曲线

2.2 单缝衍射实验

如图3所示，将缝的面积分成一组平行于缝宽的窄带，其宽度相等，从每一条窄带发出的次波振幅与窄带宽度的正比为dx。

图3 单缝实验装置图

2.3 双缝衍射实验

在双缝衍射实验中，光强分布公式为

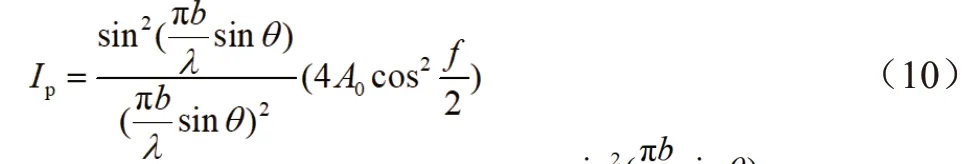
3 结束语

综上所述，杨氏双缝实验包括光的干涉与衍射两种效应，所表现的是一种暗条纹等宽、明条纹等宽的理想情况，同时受到单缝衍射调制的影响，杨氏双缝实验又分为双缝干涉实验与双缝衍射实验两种，前者是后者在b＜λ这一特殊条件下的现象，在现实中几乎无法实现，因此双缝干涉实验也是一种理想化的实验，可以将其与单缝衍射实验相结合，使其成为更加具有现实意义的综合性实验。目前，研究杨氏双缝实验的文献及报道有很多，根据计算机仿真可以更好地得出图样，但得出的图样是否真正符合实际情况，仍是需要在未来探究的重点内容，因此在理论推导与实验数据对比合理后，仍需要进一步分析各种影响因素，以更加精准地理解干涉与衍射原理。