电力系统无功优化的算法概述

柯国华 陈新河 周琪 陈芳雨

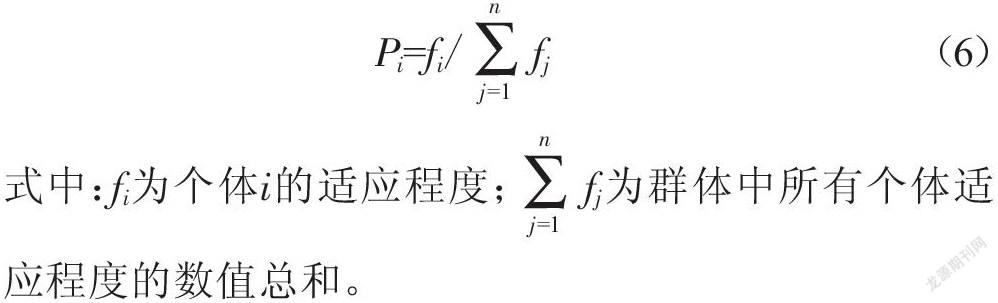
摘要：无功优化作为一种调节电网无功功率的重要手段，在减少电网有功功率消耗，保障系统的安全、经济和稳定运行，提升供电质量和可靠性方面发挥着重要作用。鉴于此，对当前流行的无功优化算法做了概括和总结，并对比说明了这些算法各自的优缺点。

关键词：电力系统;无功优化;优化算法

中图分类号：TM714.3  文献标志码：A  文章编号：1671-0797（2022）01-0083-03

DOI：10.19514/j.cnki.cn32-1628/tm.2022.01.023

0    引言

随着电网规模增大、结构复杂化、负荷多样化，大量无功产生并在网间流动，从而造成了大量有功损耗，降低了电网供电质量。无功优化是采用一种综合性的非线性分析方法[1]，对电网的各种变量进行调节和控制，使无功功率在电网中实现最优分布，从而提高电压质量、降低网损[2]。

当前热门的无功优化算法主要有粒子群算法[3]、遗传算法[4]和蚁群算法[5]等，这些算法在一定的约束条件下具有很强的全局搜索能力，通过不断迭代更新解，得到最优解。

1    无功优化数学模型

电力系统无功优化数学模型由目标方程以及各种约束条件组成[6]，由于算法优化的目的是使有功损耗最小[7]，因此其目标函数为：

式中：f为目标函数;x为状态变量;u为控制变量;Gij为节点i、j之间的电导;Ui和Uj分别为节点i、j电压的幅值;φij为节点i、j之间的电压相角差。

在无功优化中，发电机电压属于连续型变量，无功补偿设备的容量大小和变压器分接头所处位置则属于非连续型变量[8]。

无功优化的等式约束条件为：

不等式约束条件为：

2    无功优化算法介绍

当前电力系统无功优化的算法多种多样，但根据算法的原理，大体上可分为粒子群算法、遗传算法和蚁群算法3种。

2.1    标准粒子群算法

粒子群算法（Particle Swarm Optimization）是一种基于粒子模拟鸟类在空间寻食物的算法。其中每个粒子都具备自身特有的记忆属性，可将之前迭代粒子的速度与位置都记忆下来。在之后的每次迭代中，每个粒子都会追寻上次迭代过程所保存的最优粒子并不断对自身进行调整，以寻找更优解。

其基本迭代方程为[9-10]：

式中：Xi和Vi分别为一个粒子当前的位置和飞行速度;w为一种惯性因子;c1、c2为学习因子;P_best和G_best分别为一个粒子当前个体最优值和全局最优值。

此时，粒子群将按照式（4）和式（5）分别寻求个体最优解和全局最优解。

2.2    遗传算法

遗传算法（Genetic Algorithm）是模拟生物的进化、变异的一种智能算法。该算法以某个群体空间所有个体为对象，利用随机赋值参数对一个由其他个体组成的算法空间进行有效搜索，判断此算法空间适应性是否满足优化标准。若满足，则输出最优个体;否则，则依据其适应性水平来选择自己的父母，适应性水平较高者易被选取，适应性水平较低者易被淘汰。然后利用父母的染色体按一定顺序交叉生成子代，且子代染色体发生变异。遗传算法通过个别选择、交叉和变异等手段构成了遗传的基本运算。其中，在常见的轮盘赌算法中，个体i被轮盘选择的概率表示为：

2.3    蚁群算法

蚁群算法（Ant Colony Optimization）是模拟蚁群找食源时寻找最短途径的一种优化方案，该算法被应用于多种研究领域[11]。蚂蚁在行走的过程中，会释放一种叫做“信息素”的物质来标记自己的行走路径，蚂蚁根据这些信息素浓度来决定它们的行走方向。初始情况下蚂蚁行走途径是随机的，在一定时间内，较长途径上蚂蚁相对于较短途径上蚂蚁的分布密度要小得多，所以路径越短，信息素浓度越高，从而越来越多的蚁群就可能会聚集在最短的觅食路径上[12]。

在t时刻，蚂蚁k从城市x转移到城市y的概率可由以下方式计算得到[13]：

式中：τx，y（t）为蚂蚁在x城市到y城市之间的信息素的量;δx，y为启发式因子，与城市x、y之间的成本成反比，代表蚂蚁从x城市向y城市迁移的期待值;α和β分别为信息启发式因子和期望值启发式因子;Jk （x ）为在x城市处蚂蚁k可选择行走的城市集合。

3    无功优化算法对比

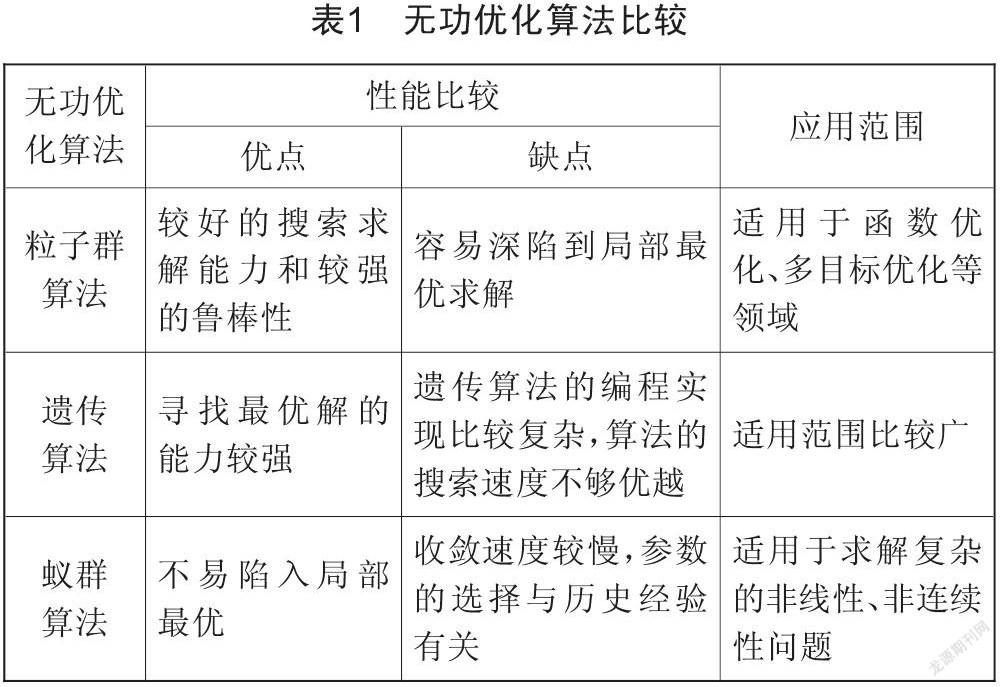
各种无功优化算法原理各不相同，造成它們各具特点，各自适应的环境也不同。

文献[14]验证了对于IEEE 30节点系统，采用粒子群算法，迭代35次即可找到最优解，且网损率可控制在5.94%。文献[9]也表明采用粒子群算法研究电力系统无功优化问题，可提高计算精确度及收敛稳定性。文献[10]则指出粒子群算法缺乏速度的动态调节，导致收敛精度不高和不易收敛，不能有效解决离散型的综合性优化问题，无法精确控制算法的参数，也无法保证整体与局部之间的平衡。

文献[15-16]指出遗传算法具有寻优能力强、程序执行简单等特征，但其编程实现较为复杂，在得到一个最优解之后就必须将问题重新编码。另外，计算因子的选取也对求解的效率和品质影响很大，而该参数的选取大多依赖经验。文献[16]表明，对于IEEE 30节点系统，遗传算法需要迭代154次，历时12 min，而改进后的遗传算法仍需6 min，搜索速度不够优越。

文献[13]显示，由于蚁群算法中每个信息素的初值相等，在选取下一个节点的过程中往往倾向于随机选取，导致该算法初期的收敛速度较慢，在参数选择上，该算法主要依靠基础知识和试错，不恰当的初始参数会大大削弱算法的寻优能力，降低算法的精确性和优化效率。文献[17]表明，蚁群算法可将城市复杂配电网无功补偿后的网损率降低到3.25%，标幺值下的最低电压可在补偿后提高到0.97 p.u.。

表1简单列出了上述3种无功优化算法的优缺点及适用环境。

4    结语

本文对比说明了常见的无功优化算法的原理及其各自的特点。面对具有多重约束、多个变量的无功优化模型，需要有针对性地选择出最适用于某种特定条件的无功优化算法。即使如此，对于收敛速度、结果准确性以及最终优化效果等指标仍然不能完全兼顾。随着对无功优化智能算法的不断探索，无功控制优化算法将朝着多分支化和相互融合两个方向发展，以适应特定条件或普适环境下电力系统的无功优化，使得待求系统优化模型更加精确，最大限度减小电网有功损耗，提高电网输电效率和电能质量。

[参考文献]

[1] 曹琪琳，胡卫华.电力市场无功优化分析[J].华电技术，2008（10）：19-21.

[2] 葛莲.基于混合智能算法的电力系统无功优化研究[D].兰州：兰州交通大学，2012.

[3] 袁晓辉，王乘，张勇传，等.粒子群优化算法在电力系统中的应用[J].电网技术，2004，28（19）：14-19.

[4] 马晋弢，杨以涵.遗传算法在电力系统无功优化中的应用[J].中国电机工程学报，1995（5）：347-353.

[5] 林昭华，侯云鹤，熊信艮，等.广义蚁群算法用于电力系统无功优化[J].华北电力大学学报（自然科学版），2003（2）：6-9.

[6] 孙建鹏，韩文花，朱长东.电力系统无功优化模型及算法研究[J].电力电容器与无功补偿，2011，32（6）：6-11.

[7] 徐晓静，孙明灿，陈庆春，等.同步关合技术在无功补偿中的应用[J].高压电器，2007，43（5）：333-335.

[8] 刘凯，申小敏，陈志江.电力系统无功优化研究的进展与展望[J].黑龙江电力，2014，36（4）：305-309.

[9] 张建科，刘三阳，张晓清.改进的粒子群算法[J].计算机工程与设计，2007，28（17）：4215-4216.

[10] 曾令全，罗富宝，丁金嫚.禁忌搜索-粒子群算法在无功优化中的应用[J].电网技术，2011，35（7）：129-133.

[11] 胡小兵，黄席樾.基于混合行为蚁群算法的研究[J].控制与决策，2005，20（1）：69-72.

[12] 李秀卿，王涛，王凯，等.基于蚁群算法和内点法的无功优化混合策略[J].继电器，2008，36（1）：22-26.

[13] 许崇耀，陈维伟，王翔宇，等.基于改进蚁群算法的无功优化研究[J].黑龙江电力，2013，35（6）：501-504.

[14] 黄博，曾驰宇，王全胜，等.一种求解电力系统无功优化的改进粒子群算法[J].电工技术，2020（12）：107-109.

[15] 张粒子，舒隽，林宪枢，等.基于遗传算法的无功规划优化[J].中国电机工程学报，2000，20（6）：5-8.

[16] 顾洁，陈章潮，张林.基于遗传算法的无功优化模型研究[J].电力系统及其自动化学报，2001，13（3）：10-12.

[17] 郭恒，羅可，唐贤瑛.基于蚂蚁算法的配电网无功优化[J].电力电容器，2005（4）：21-24.

收稿日期：2021-09-17

作者简介：柯国华（2000—），女，安徽合肥人，研究方向：电力系统无功优化。

通信作者：陈新河（1976—），男，安徽宣城人，硕士，副教授，研究方向：算法设计、软件设计、电子电路。